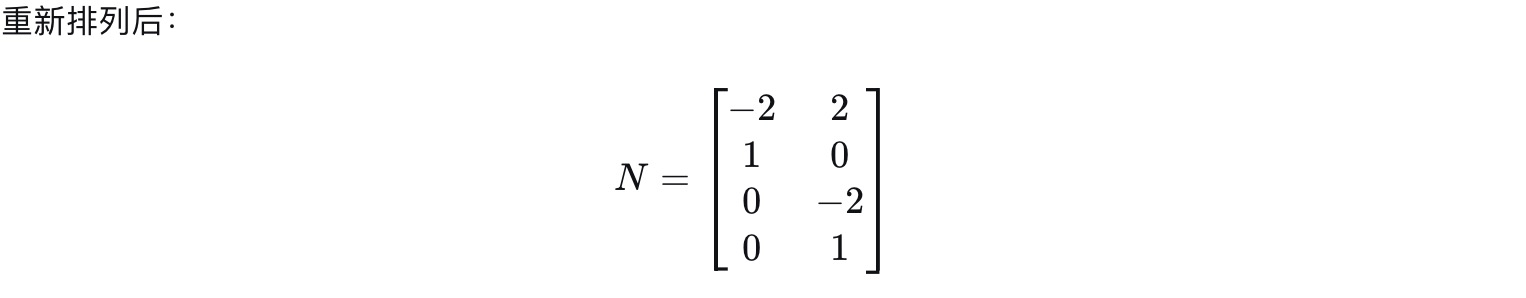2.3 矩阵的零空间

1.高斯消元法求矩阵的零空间

2.行最简形式求矩阵的零空间

1.高斯消元法求矩阵的零空间

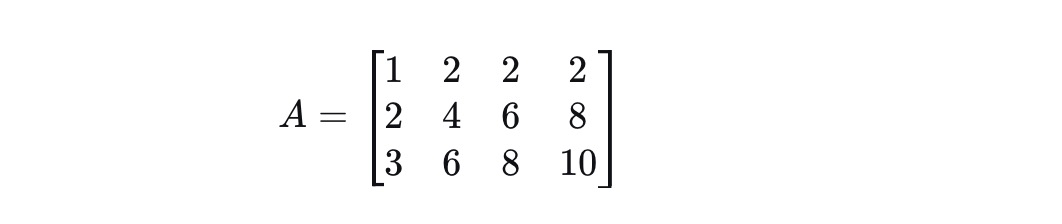
csharp 复制代码

1).对矩阵进行高斯消元

a.第2行 = 第2行 - 2 × 第1行

b.第3行 = 第3行 - 3 × 第1行

c.第3行 = 第3行 - 第2行

csharp 复制代码

2).识别主元和自由变量

a.主元位置: 第一列和第三列

b.主元变量: x1, x3

c.自由变量: x2, x4

csharp 复制代码

3).回代求解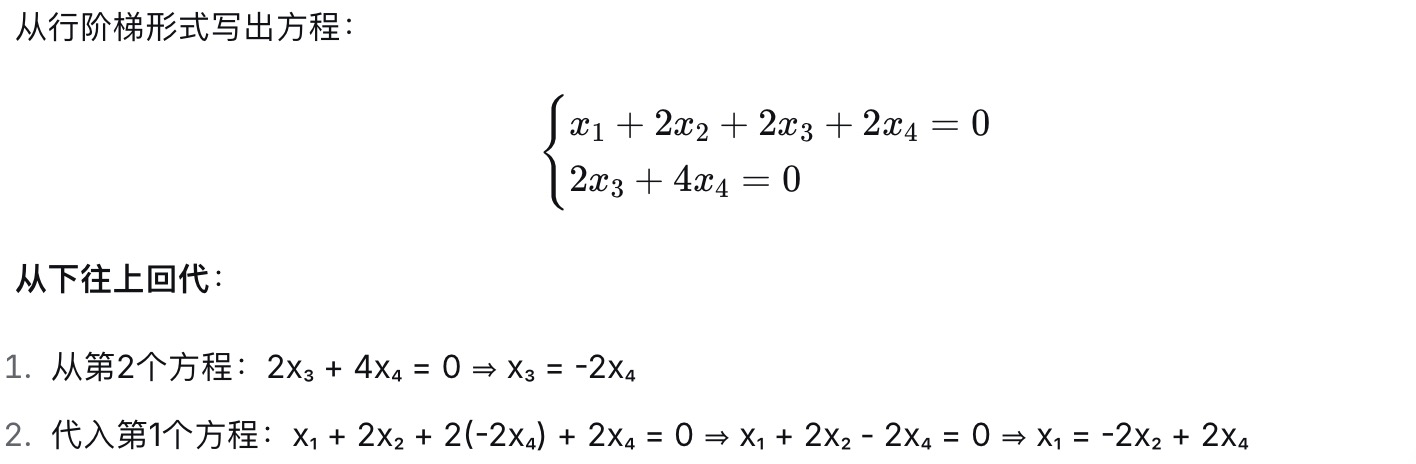

csharp 复制代码

4).将x1, x2, x3, x4写为列向量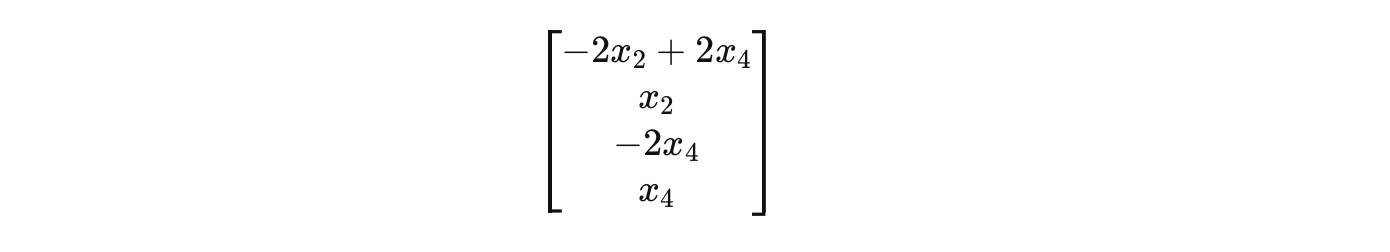

csharp 复制代码

将x2, x4提出, 得出方程Ax = 0的解; 下面的形式表示方程的通解

注: "零空间中自由变量对应的是单位向量"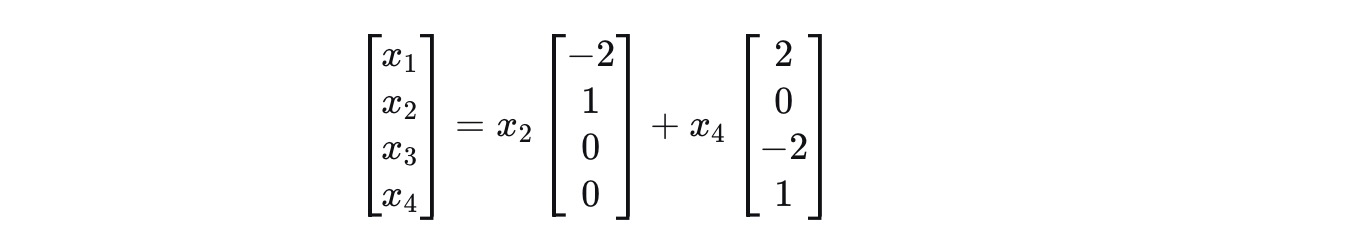

csharp 复制代码

假设有n个变量, r个主元(即秩为r), 那么自由变量的个数为n - r

我们构造零空间基向量的目标是找到n - r个线性无关的向量, 使得这些向量的任意线性组合都

是方程的解, 并且这些向量张成整个零空间

方法如下:

a.每次令一个自由变量取1, 其余自由变量取0

b.通过回代(或直接从行最简形式)求出基本变量的值

c.为什么自由变量部分要取单位向量? 因为这样构造的向量是线性无关的

csharp 复制代码

下面的向量称为方程的特解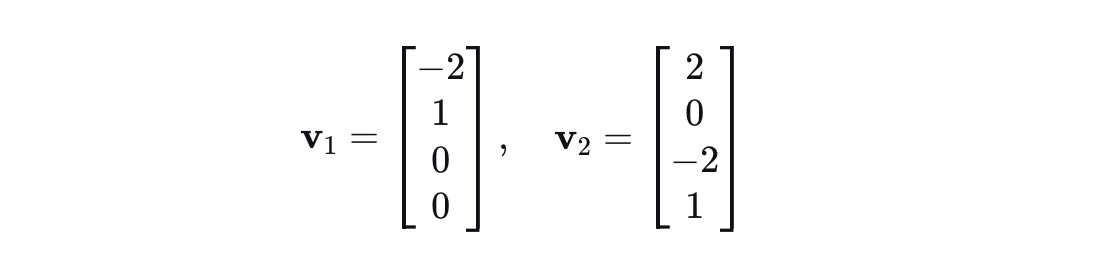

csharp 复制代码

矩阵A的零空间是"Ax = 0的特解的线性组合成", 特解的个数就等于自由变量的个数, 因为

每一个自由变量对应一个特解

2.行最简形式求矩阵的零空间

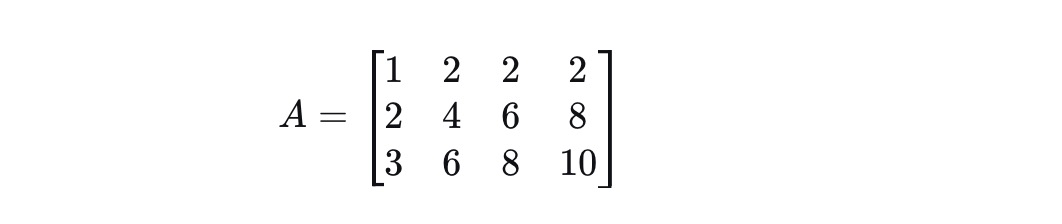
csharp 复制代码

1).将矩阵化为行最简形式

a.第2行 = 第2行 - 2 × 第1行

b.第3行 = 第3行 - 3 × 第1行

c.第3行 = 第3行 - 第2行

d.第2行 = 第2行 ÷ 2

e.第1行 = 第1行 - 2 × 第2行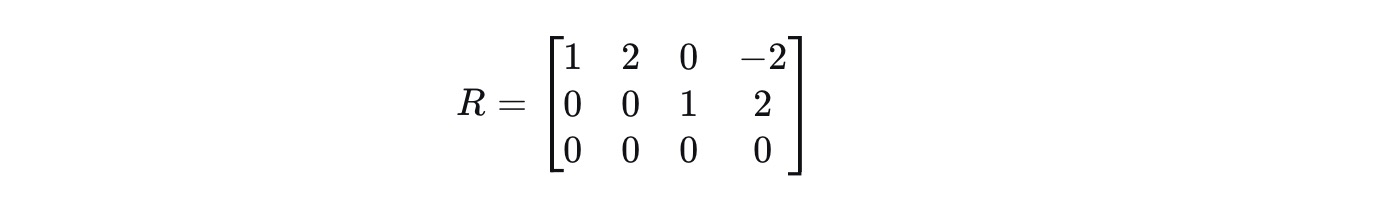

csharp 复制代码

2).观察通过高斯消元法求解的特解矩阵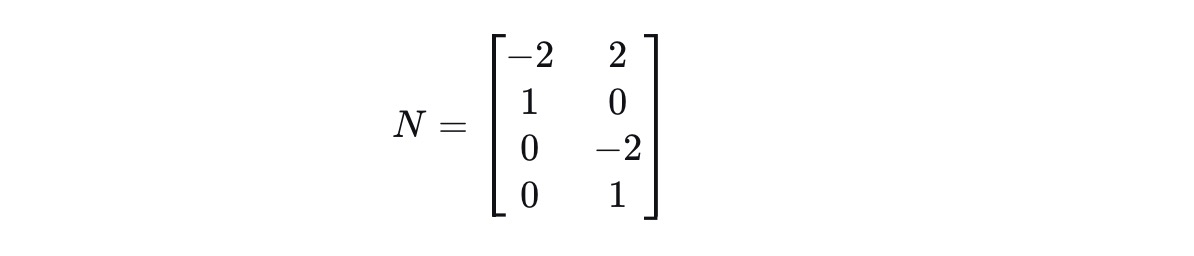

csharp 复制代码

3).将R矩阵分为单位矩阵和F的形式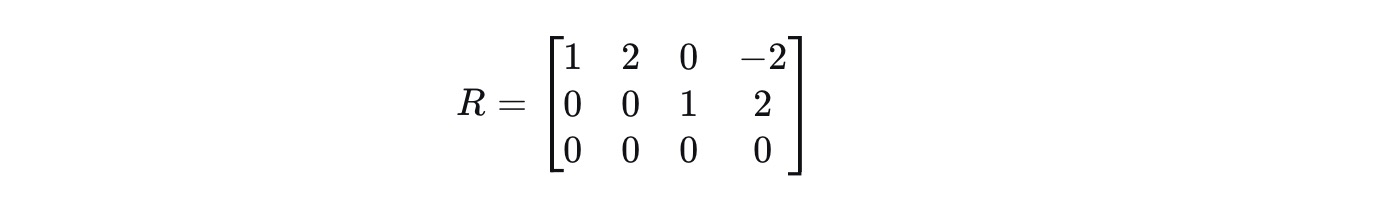

csharp 复制代码

将特解矩阵分为单位矩阵和-F的形式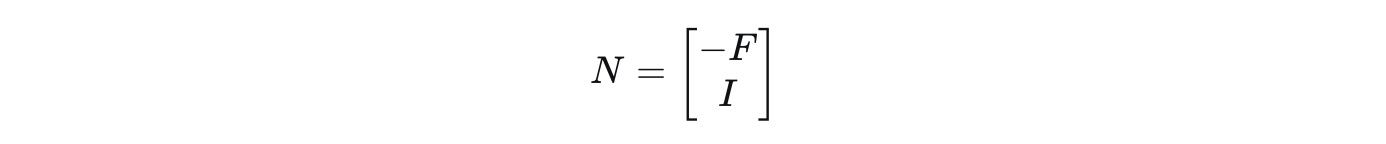

csharp 复制代码

实例: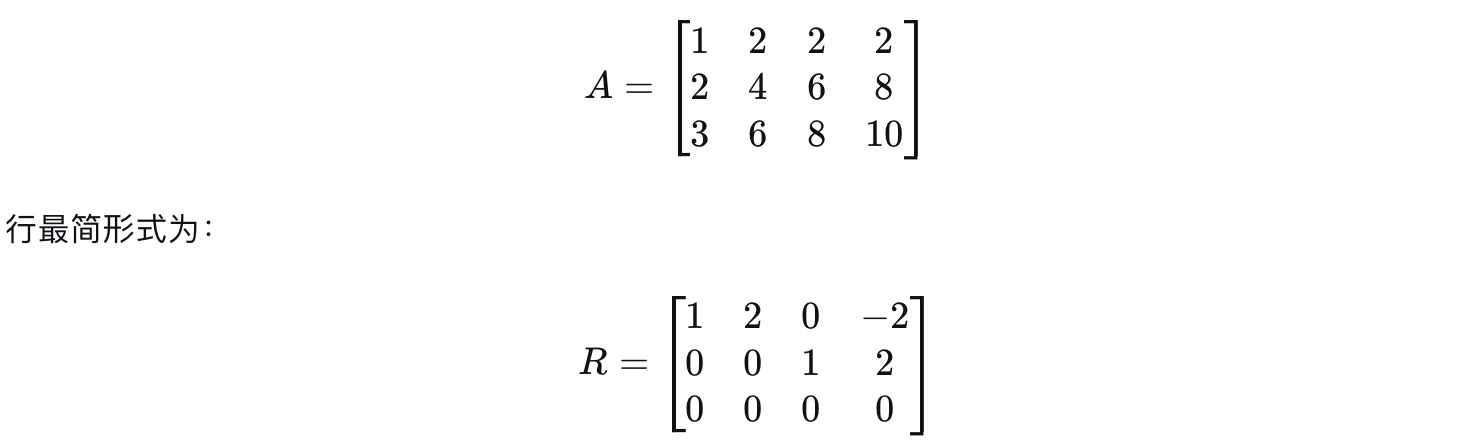

csharp 复制代码

1).识别基本变量和自由变量

a.主元列: 第1列和第3列

b.基本变量: x₁, x₃

c.自由变量: x₂, x₄

csharp 复制代码

2).构造F矩阵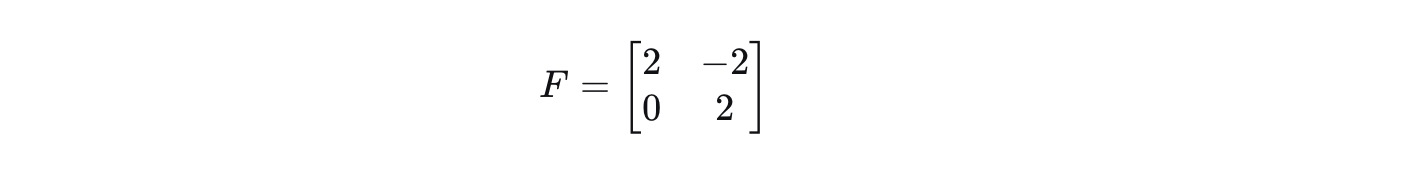

csharp 复制代码

3).构造零矩阵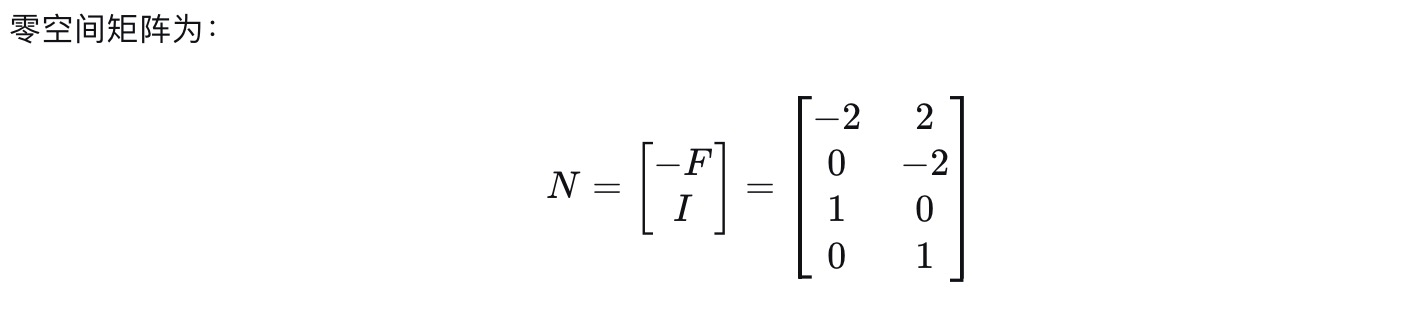

csharp 复制代码

我们的自由向量是x2, x4, 自由向量对应的值的单位向量, 因此需要交换第二行和第三行的

顺序