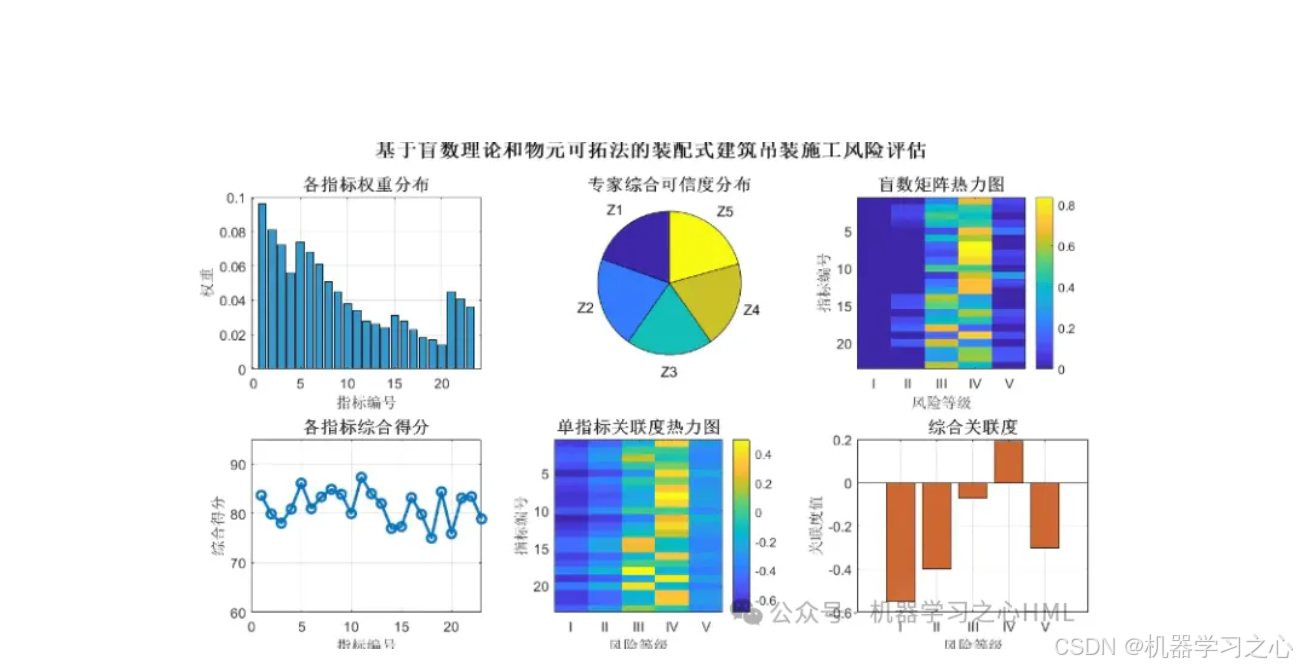
模型核心思想
该模型的核心思想在于:
- 利用盲数处理不确定性:装配式建筑吊装风险因素(如人员经验、设备状态、风速等)的评估常常是模糊的、不完整的,难以用精确数值表示。盲数理论能够通过"盲数"形式,同时表达数据的取值区间和在该区间内的可信度分布,从而更科学地量化专家经验判断。
- 利用物元可拓进行等级评估:物元可拓法通过建立风险等级的标准物元和待评估物元,计算它们之间的关联度,从而精确地将风险水平定位到某个等级。它能处理"既是又非"的过渡状态,非常适合风险等级这种界限模糊的评判。
模型构建步骤
步骤一:建立风险评估指标体系
首先,需要系统地识别装配式建筑吊装施工过程中的所有潜在风险因素,并建立层次化的指标体系。
- 目标层(A):装配式建筑吊装施工综合风险评估值。
- 准则层(B) :通常可从"人、机、料、法、环、管"等维度展开。例如:
- B1:人员因素
- B2:机械设备因素
- B3:构件与材料因素
- B4:技术工艺因素
- B5:环境因素
- B6:管理因素
- 指标层(C) :在每个准则层下细分具体指标。例如:
- C11:指挥司索工技能与经验
- C12:吊装工人安全意识
- C21:塔吊/汽车吊性能与状况
- C22:吊索具完好率
- C51:天气条件(风速、雨雪)
- C52:作业空间复杂性
- ...等等。
步骤二:确定指标权重
采用AHP(层次分析法)或熵权法等方法来确-定各层级指标的权重向量 W 。为了结合盲数,可以邀请多位专家用盲数的形式进行两两比较判断。
盲数表达示例:专家认为指标i比指标j"略微重要",但不确定程度,他可能给出一个区间判断,如"介于2和4之间",并给出一个可信度分布,如"在2-3之间的可能性是40%,在3-4之间的可能性是60%"。这个判断就可以表示为一个盲数。
步骤三:建立风险等级标准物元
定义施工风险等级,例如:Ⅰ级(低风险)、Ⅱ级(一般风险)、Ⅲ级(较高风险)、Ⅳ级(高风险)。
对于每个底层指标 C_i ,规定其在不同风险等级下的取值范围,构建经典域物元 R_j 和节域物元 R_P 。
-
经典域物元 R_j :
R_j = (N_j, C_i, V_{ji}) = \\begin{bmatrix} N_j \& C_1 \& (a_{j1}, b_{j1}) \\ \& C_2 \& (a_{j2}, b_{j2}) \\ \& \\vdots \& \\vdots \\ \& C_n \& (a_{jn}, b_{jn}) \\end{bmatrix}
其中, N_j 表示第 j 个风险等级, (a_{ji}, b_{ji}) 表示等级 j 下关于指标 C_i 的量值范围。
-
节域物元 R_P :
R_P = (P, C_i, V_{Pi}) = \\begin{bmatrix} P \& C_1 \& (a_{P1}, b_{P1}) \\ \& C_2 \& (a_{P2}, b_{P2}) \\ \& \\vdots \& \\vdots \\ \& C_n \& (a_{Pn}, b_{Pn}) \\end{bmatrix}
其中,P 表示所有风险等级的全体,(a_{Pi}, b_{Pi}) 是指标 C_i 在所有等级下的总取值范围。
步骤四:获取待评物元(基于盲数)
这是模型的关键创新点。邀请多位专家对当前项目的各个底层指标 C_i 的风险状态进行评估。由于不确定性,专家给出的不是一个确切的分数,而是一个盲数评估值。
- 专家评估:对于指标 C_i ,专家 k 可能给出:"我认为风险值在60到80之间,其中60-70的可能性为30%,70-80的可能性为70%。"
- 形成盲数:这个评估可以表示为一个盲数 \\tilde{x}_i\^k 。
- 综合专家意见 :将所有 m 位专家对同一指标 C_i 的盲数评估进行加权平均或集结,得到该指标的综合盲数评估值 \\tilde{x}_i 。
待评物元 R 可表示为:
R = \\begin{bmatrix} P \& C_1 \& \\tilde{x}_1 \\ \& C_2 \& \\tilde{x}_2 \\ \& \\vdots \& \\vdots \\ \& C_n \& \\tilde{x}_n \\end{bmatrix}
步骤五:计算盲数关联度
计算待评物元 R 关于各风险等级 N_j 的盲数关联度 K_j(\\tilde{x}_i) 。
首先,计算单个指标 C_i 的盲数 \\tilde{x}_i 相对于等级 j 的关联度。这需要用到盲数距离公式。关联度函数基于物元可拓理论中的距的概念:
K_j(x) = \\begin{cases} \\frac{-\\rho(x, V_{ji})}{\|V_{ji}\|} \& x \\in V_{ji} \\ \\frac{\\rho(x, V_{ji})}{\\rho(x, V_{Pi}) - \\rho(x, V_{ji})} \& x \\notin V_{ji} \\end{cases}
由于 x 在这里是盲数 \\tilde{x}_i ,计算 \\rho(\\tilde{x}*i, V* {ji}) 和 \\rho(\\tilde{x}*i, V*{Pi}) 需要用到盲数运算规则,最终得到的 K_j(\\tilde{x}_i) 也是一个盲数,它表示指标 C_i 属于等级 j 的可信度分布情况。
步骤六:确定综合风险等级
-
计算综合关联度 :将各指标的盲数关联度 K_j(\\tilde{x}_i) 与其权重 w_i 进行加权合成,得到待评项目相对于风险等级 j 的综合盲数关联度 \\tilde{K}_j 。
\\tilde{K}*j = \\sum*{i=1}\^{n} w_i \\cdot K_j(\\tilde{x}_i)
-
盲数清晰化:将综合盲数关联度 \\tilde{K}_j 通过清晰化计算(如求其期望值 E\[\\tilde{K}_j\] ),得到一个确定的数值 K_j 。
-
等级判定:根据最大关联度准则,若 K_{j0} = \\max_{j \\in {1,2,3,4}} K_j ,则判定该吊装施工项目的综合风险等级为 j0 。
模型优势
- 信息利用充分:盲数理论能够有效处理和融合专家判断中的区间性和不确定性,避免了传统方法中强行将模糊信息精确化造成的信息失真。
- 评估结果精确:物元可拓法通过关联函数进行定量计算,评估结果比单纯的模糊综合评判更精细,能反映出风险状态与标准等级之间的"距离"。
- 动态适应性:当施工条件变化时,只需更新待评物元中的盲数值,即可快速进行重新评估,模型实用性强。
- 系统性:该模型将定性与定量分析、主观与客观信息有机地结合在一起,形成了一个系统、科学的评估流程。
应用示例
问题:评估某PC项目吊装施工的"环境因素(B5)"风险。
- 指标:C51(风速),C52(作业空间)。
- 权重:W = (0.6, 0.4)。
- 风险等级:设4个等级,经典域(以C51为例):Ⅰ级(0, 10) km/h,Ⅱ级(10, 20),Ⅲ级(20, 30),Ⅳ级(30, 50)。
- 专家盲数评估 :
- C51(风速):两位专家综合后,认为当前风速风险值为 \\tilde{x}_1 = {[15,20], 0.7; [20,25], 0.3} (即15-20的可能性70%,20-25的可能性30%)。
- C52(作业空间):评估值为 \\tilde{x}_2 = {[60,70], 0.4; [70,80], 0.6}。
- 计算关联度 :
- 计算 \\tilde{x}_1 , \\tilde{x}_2 相对于四个等级的盲数关联度 K_1(\\tilde{x}_1), K_2(\\tilde{x}_1)... 。
- 加权合成得到综合盲数关联度 \\tilde{K}_j 。
- 清晰化后得到 K_1 = -0.52, K_2 = 0.15, K_3 = -0.21, K_4 = -0.65 。
- 结果 :\\max K_j = K_2 = 0.15 ,因此"环境因素"风险等级为 Ⅱ级(一般风险)。
结论
基于盲数理论和物元可拓法的装配式建筑吊装施工风险评估模型,有效地解决了风险评估过程中的不确定性和模糊性问题,提供了一条科学、严谨、实用的风险量化路径。该模型不仅适用于吊装施工,经过适当调整后,也可推广到装配式建筑全生命周期的其他风险分析领域,具有很高的理论价值和实践指导意义。