8.1 集成学习基础知识
8.1.1 集成学习的概念
集成学习将多个性能一般的普通模型进行有效集成,形成一个性能优良的集成模型,通常将这种性能一般的普通模型称为个体学习器。
如果所有个体学习器都属于同类模型,则称由这些个体学习器产生的集成模型为同质集成模型,并称这些属于同类模型的个体学习器为基学习器。
反之,将属于不同类型的个体学习器进行组合产生的集成模型称为异质集成模型。
若某学习问题能被个体学习器高精度地学习,则称该学习问题是强可学习问题,并称相应个体学习器为强学习器;反之,则可定义弱可学习问题,并称相应个体学习器为弱学习器。当直接构造其强学习器比较困难时,可通过构造一组弱学习器生成强学习器,将强可学习问题转化为弱可学习问题。通常称集成学习在分类任务中的弱(强)学习器为弱(强)分类器,在回归任务中弱(强)学习器为 弱(强)回归器。
合理地选择弱学习器是集成学习首要必须解决的问题,例如,对于图 5-1 所示的二分类任务(圆圈表示分类正确,叉号表示分类错误),图中每个分类器的分类正确率均为1/3,则由少数服从多数原则进行组合得到集成模型的分类正确率为 0。
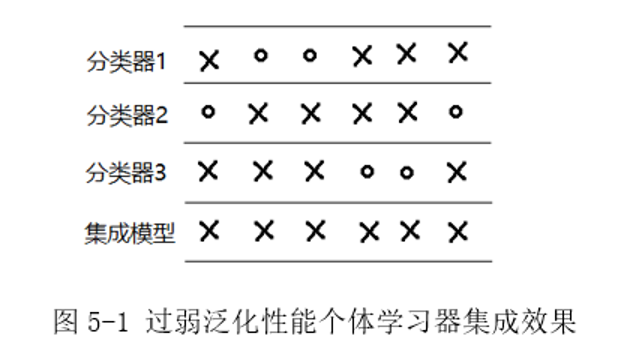
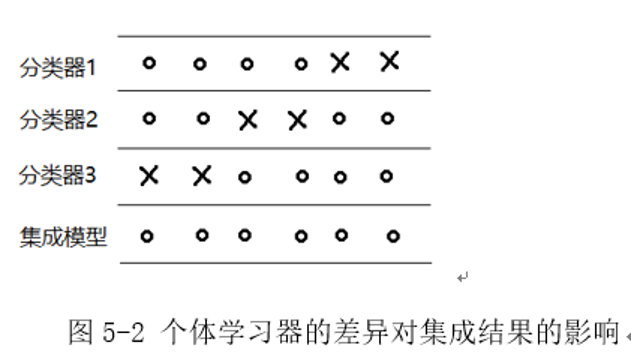
上述情况是由于弱学习器泛化性能均太弱造成的。在集成学习的实际应用当中,应尽可能选择泛化性能较强的弱学习器进行组合,如图5-2所示,当每个弱分类器分类错误的样本各不相同时,则能得到一个效果优异的集成模型。
8.1.2 集成学习基本范式
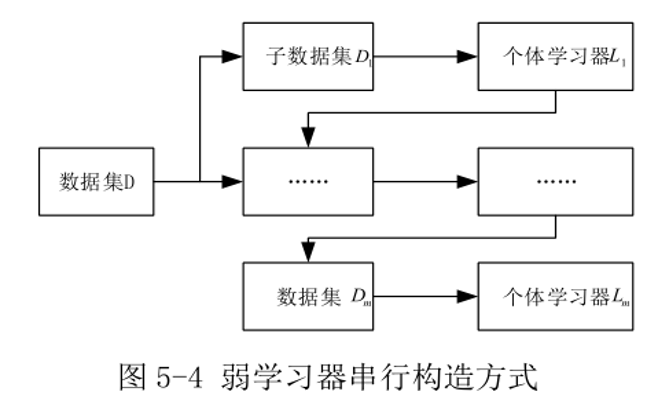
集成学习包括两个基本步骤:
(1)首先根据数据集构造弱学习器
(2)对弱学习器进行组合得到集成模型
集成学习中回归任务的弱学习器组合策略 ------ 简单平均法

集成学习中回归任务的弱学习器组合策略------加权平均法

集成学习分类任务中弱分类器的相对多数投票法

集成学习分类任务中弱分类器的绝对多数投票法

集成学习分类任务中的加权投票法


8.1.3 集成学习泛化策略
集成学习回归任务中简单平均法的误差定义

集成学习中弱回归器的差异度(多样性)指标

集成模型误差与弱回归器平均误差、差异度的关系

降低弱学习器的泛化误差: 样本扩充、范数惩罚等机器学习正则化策略。作用:通过增加训练数据的覆盖性(样本扩充),或限制模型复杂度(范数惩罚,如 L1/L2 正则),减少弱学习器自身的过拟合风险,提升其基础预测能力。
提高个体学习器的多样性:改变训练样本和改变模型训练参数。作用:通过调整训练数据分布(如 Bagging 的随机抽样)或模型参数(如不同的初始化权重、学习率),让各弱学习器的预测结果产生差异,从而增强集成后模型的方差抑制效果。

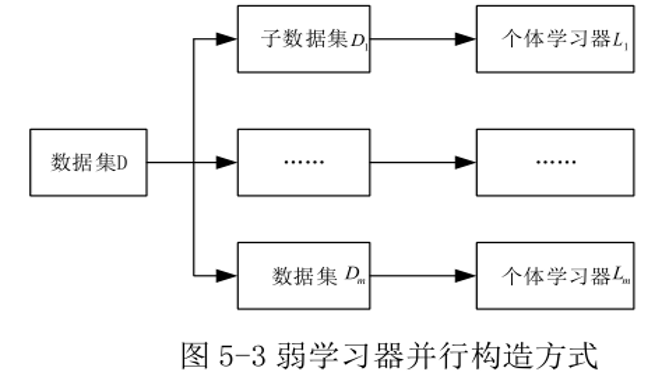
改变训练样本的角度:通过对样本数据采样增加输入样本随机性,由此提高弱学习器多样性。具体地说,通过样本数据集D构造m个不同的弱学习器,使用某种采样方法从D生成m个有差别的训练样本数据子集{D_1,D_2,...,D_m},分别用这些训练子集进行训练就可以构造出m个有差别弱学习器。

改变模型训练参数的角度:由于弱学习器自身参数的不同设置以及在不同训练阶段的产生的不同参数也会产生不同的弱学习器,故可从改变神经网络初始连接权重、隐层神经元个数等参数的角度增加弱学习器的多样性。 通常综合使用多种泛化策略构造同一个集成模型。 例如在构建某个集成模型时可能既采用数据样本采样方法,又对模型参数进行随机选择以提高弱学习器的多样性。

弱学习器个数对集成模型泛化性能的影响

8.2 Bagging集成学习
8.2.1 Bagging集成策略
Bagging 集成学习中自助采样法的核心流程与作用

Bagging 集成学习的完整流程及集成策略
例题 5.1


代码实现
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.utils import resample
import matplotlib.pyplot as plt
# ---------------------- 1. 加载题目中的真实数据 ----------------------
X = np.array([4.2, 7.1, 6.3, 1.1, 0.2, 4.0, 3.5, 8, 2.3]).reshape(-1, 1)
y = np.array([8600, 6100, 6700, 12000, 14200, 8500, 8900, 6200, 11200])
# 打印原始数据集信息
print("=" * 50)
print("【原始数据集信息】")
print(f"距离X(km):{X.flatten()}")
print(f"房价y(元/㎡):{y}")
print(f"样本总数:{len(X)}个")
print("=" * 50 + "\n")
# ---------------------- 2. Bagging参数设置 ----------------------
n_estimators = 3
estimators = []
predictions = []
target_X = 5.5 # 待预测的距离
colors = ['orange', 'green', 'red'] # 3个弱学习器的颜色区分
labels = [f'弱学习器{i + 1}' for i in range(n_estimators)] # 弱学习器标签
# ---------------------- 3. 自助采样+训练弱学习器 ----------------------
for i in range(n_estimators):
print(f"---------- 第{i + 1}个弱学习器训练过程 ----------")
# 自助采样
X_resampled, y_resampled = resample(X, y, n_samples=len(X), random_state=i)
print(f"自助采样后的距离X子集:{X_resampled.flatten().round(2)}")
print(f"自助采样后的房价y子集:{y_resampled}\n")
# 训练线性回归模型
lr = LinearRegression()
lr.fit(X_resampled, y_resampled)
estimators.append(lr)
# 输出模型参数
a = lr.coef_[0]
b = lr.intercept_
print(f"模型参数:y = {a:.2f} * X + {b:.2f}")
# 预测目标值
y_pred = lr.predict([[target_X]])[0]
predictions.append(y_pred)
print(f"对X={target_X}km的房价预测:{y_pred:.2f}元/㎡\n")
# ---------------------- 4. 集成预测(简单平均法) ----------------------
ensemble_pred = np.mean(predictions)
print("=" * 50)
print(f"【Bagging集成模型最终结果】")
print(f"3个弱学习器的预测结果:{[round(p, 2) for p in predictions]} 元/㎡")
print(f"集成预测结果(平均值):{ensemble_pred:.2f} 元/㎡")
print("=" * 50)
# ---------------------- 5. 可视化部分(修复字体警告) ----------------------
# 方案1:使用支持上标的中文字体(优先推荐)
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimSun', 'DejaVu Sans'] # 雅黑/宋体/默认英文体(均支持上标)
plt.rcParams['axes.unicode_minus'] = False # 支持负号
plt.figure(figsize=(12, 8))
# 绘制原始数据点
plt.scatter(X, y, color='blue', s=120, alpha=0.8, label='原始数据样本', edgecolors='black')
# 生成拟合线的X范围(覆盖原始数据的X区间,使拟合线更完整)
X_line = np.linspace(X.min() - 0.5, X.max() + 0.5, 100).reshape(-1, 1)
# 绘制每个弱学习器的拟合线和预测点
for i, (lr, color, label) in enumerate(zip(estimators, colors, labels)):
# 绘制拟合线
y_line = lr.predict(X_line)
# 模型公式简化为整数系数,更易读
a_round = round(lr.coef_[0])
b_round = round(lr.intercept_)
plt.plot(X_line, y_line, color=color, linewidth=2.5, label=f'{label} 拟合线:y={a_round}X+{b_round}')
# 绘制该弱学习器对target_X的预测点(单位用"元/平米"避免上标)
plt.scatter(target_X, predictions[i], color=color, s=150, marker='s',
label=f'{label} 预测点({target_X}, {predictions[i]:.2f}元/平米)', edgecolors='black')
# 绘制集成预测点(突出显示)
plt.scatter(target_X, ensemble_pred, color='purple', s=250, marker='*',
label=f'集成预测点({target_X}, {ensemble_pred:.2f}元/平米)', edgecolors='black', zorder=5)
# 图表美化与标注(单位统一为"元/平米")
plt.xlabel('房屋到市中心的距离(km)', fontsize=14)
plt.ylabel('房价(元/平米)', fontsize=14) # 替换"元/㎡"为"元/平米",彻底避免上标
plt.title('Bagging集成线性回归:弱学习器拟合与预测结果可视化', fontsize=16, fontweight='bold', pad=20)
plt.legend(fontsize=11, loc='upper right', bbox_to_anchor=(1, 1)) # 图例位置调整
plt.grid(True, alpha=0.3, linestyle='--') # 网格线
plt.xlim(X.min() - 0.8, X.max() + 0.8) # X轴范围微调
plt.ylim(min(y.min(), min(predictions)) - 500, max(y.max(), max(predictions)) + 500) # Y轴范围微调
# 保存图片(无警告)
plt.savefig('bagging_visualization.png', dpi=300, bbox_inches='tight')
plt.show()运行结果
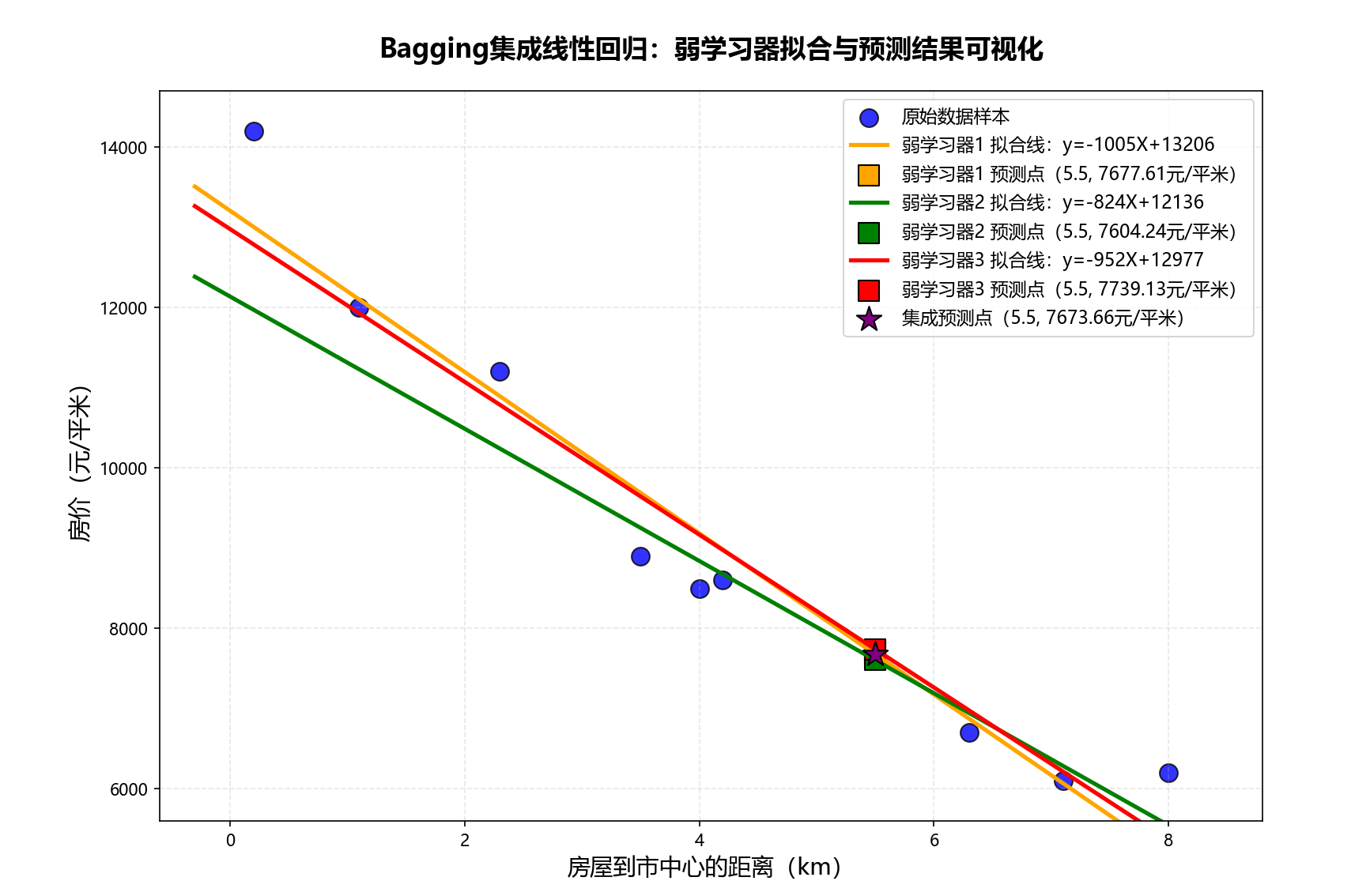
==================================================
【原始数据集信息】
距离X(km):[4.2 7.1 6.3 1.1 0.2 4. 3.5 8. 2.3]
房价y(元/㎡):[ 8600 6100 6700 12000 14200 8500 8900 6200 11200]
样本总数:9个
==================================================
---------- 第1个弱学习器训练过程 ----------
自助采样后的距离X子集:[4. 4.2 1.1 1.1 8. 1.1 4. 6.3 0.2]
自助采样后的房价y子集:[ 8500 8600 12000 12000 6200 12000 8500 6700 14200]
模型参数:y = -1005.20 * X + 13206.24
对X=5.5km的房价预测:7677.61元/㎡
---------- 第2个弱学习器训练过程 ----------
自助采样后的距离X子集:[4. 2.3 4. 4.2 4.2 7.1 8. 3.5 6.3]
自助采样后的房价y子集:[ 8500 11200 8500 8600 8600 6100 6200 8900 6700]
模型参数:y = -824.04 * X + 12136.47
对X=5.5km的房价预测:7604.24元/㎡
---------- 第3个弱学习器训练过程 ----------
自助采样后的距离X子集:[2.3 2.3 3.5 6.3 2.3 8. 6.3 7.1 4. ]
自助采样后的房价y子集:[11200 11200 8900 6700 11200 6200 6700 6100 8500]
模型参数:y = -952.41 * X + 12977.39
对X=5.5km的房价预测:7739.13元/㎡
==================================================
【Bagging集成模型最终结果】
3个弱学习器的预测结果:[7677.61, 7604.24, 7739.13] 元/㎡
集成预测结果(平均值):7673.66 元/㎡
==================================================
例题5.2


代码实现
import numpy as np
import random
import matplotlib.pyplot as plt
# ---------------------- 全局配置(避免中文显示问题) ----------------------
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
# 使用默认英文兼容字体,避免中文标签显示异常
try:
plt.style.use('seaborn-v0_8-whitegrid') # 图表风格(兼容新版本)
except:
plt.style.use('default') # 旧版本降级使用默认风格
# ---------------------- 1. 准备数据集(产品属性X + 类标签y) ----------------------
"""
数据集说明:
- X:产品的连续属性(例如质量评分、价格等),共10个样本
- y:类标签(1/-1),代表两类产品(例如合格/不合格、畅销/滞销)
"""
X = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]) # 产品属性
y = np.array([1, 1, 1, -1, -1, -1, -1, -1, 1, 1]) # 类标签
n_samples = len(X) # 样本总数:10
class_colors = {1: '#FF6B6B', -1: '#4ECDC4'} # 类别颜色映射(红色=1,青色=-1)
# ---------------------- 2. 定义弱分类器(基于阈值α的简单分类器) ----------------------
def train_weak_classifier(sub_X, sub_y):
"""
训练单个弱分类器:找到最优阈值α,使子数据集上的分类错误率最小
弱分类器逻辑:基于单个特征的阈值划分(决策树桩)
分类规则:若 X < α → 预测为1;若 X > α → 预测为-1(阈值两侧为不同类别)
参数:
sub_X: 子数据集的属性(一维数组)
sub_y: 子数据集的标签(一维数组)
返回:
h: 训练好的弱分类器函数(输入x,输出预测标签1/-1)
best_alpha: 最优阈值(使错误率最小)
best_error: 子数据集上的最小错误率
"""
best_error = float('inf') # 初始化最小错误率为无穷大
best_alpha = 0.0 # 初始化最优阈值
# 生成所有可能的阈值(取相邻样本属性的中点,覆盖所有可能划分)
sorted_indices = np.argsort(sub_X) # 对子数据集属性排序(确保相邻样本连续)
sorted_sub_X = sub_X[sorted_indices]
thresholds = [(sorted_sub_X[i] + sorted_sub_X[i + 1]) / 2 for i in range(len(sorted_sub_X) - 1)]
thresholds = list(set(thresholds)) # 去重(避免重复阈值)
thresholds.sort() # 排序阈值(便于遍历)
# 遍历所有候选阈值,找到最优解
for alpha in thresholds:
# 根据当前阈值预测标签
y_pred = np.where(sub_X < alpha, 1, -1) # X<α→1,X>α→-1
# 计算错误率(错误样本数/总样本数)
error = np.sum(y_pred != sub_y) / len(sub_y)
# 更新最优阈值和最小错误率
if error < best_error:
best_error = error
best_alpha = alpha
# 定义弱分类器函数(闭包,保存最优阈值α)
def weak_classifier(x):
return 1 if x < best_alpha else -1
return weak_classifier, best_alpha, best_error
# ---------------------- 3. Bagging集成:训练多个弱分类器 ----------------------
"""
Bagging核心逻辑:
1. 有放回抽样(Bootstrap):从原数据集随机有放回抽取n个样本,生成子数据集(与原数据集大小相同)
2. 并行训练:每个子数据集独立训练1个弱分类器(共训练5个)
3. 保存结果:记录每个弱分类器的函数、阈值、子数据集错误率
"""
n_classifiers = 5 # 弱分类器数量(可调整,通常越多泛化能力越强,但计算成本增加)
weak_classifiers = [] # 存储所有弱分类器函数
weak_alphas = [] # 存储每个弱分类器的最优阈值
weak_sub_errors = [] # 存储每个弱分类器在子数据集上的错误率
sub_datasets = [] # 存储每个子数据集的索引(用于后续可视化)
print("=" * 70)
print("Bagging集成学习 - 弱分类器训练过程")
print("=" * 70)
for i in range(n_classifiers):
# 步骤1:有放回抽样生成子数据集
sample_indices = [random.randint(0, n_samples - 1) for _ in range(n_samples)]
sub_X = X[sample_indices] # 子数据集属性
sub_y = y[sample_indices] # 子数据集标签
sub_datasets.append(sample_indices) # 保存抽样索引
# 步骤2:训练弱分类器
h, alpha, sub_error = train_weak_classifier(sub_X, sub_y)
# 步骤3:保存结果
weak_classifiers.append(h)
weak_alphas.append(alpha)
weak_sub_errors.append(sub_error)
# 打印训练信息
print(f"弱分类器{i + 1}:阈值α={alpha:.2f} | 子数据集错误率={sub_error:.2f} | 抽样索引={sample_indices}")
# ---------------------- 4. 集成模型:多数投票法组合弱分类器 ----------------------
def ensemble_predict(x):
"""
集成模型预测逻辑:多数投票法
1. 所有弱分类器对输入x进行预测,得到投票结果列表
2. 统计投票和:sum(votes),正数表示1类占优,负数表示-1类占优
3. 返回投票结果(符号函数:正数→1,负数→-1)
"""
votes = [h(x) for h in weak_classifiers] # 每个弱分类器的投票结果
return 1 if sum(votes) >= 0 else -1 # 多数投票(≥0表示1类获胜)
# ---------------------- 5. 误差分析(评估模型性能) ----------------------
"""
评估指标:错误率(原数据集上预测错误的样本数/总样本数)
对比目标:单个弱分类器的错误率 vs 集成模型的错误率
"""
# 计算每个弱分类器在原数据集上的错误率
weak_test_errors = []
for idx, h in enumerate(weak_classifiers):
y_pred = np.array([h(x) for x in X]) # 弱分类器对原数据集的预测
error = np.sum(y_pred != y) / n_samples # 错误率
weak_test_errors.append(error)
# 计算集成模型在原数据集上的错误率
ensemble_y_pred = np.array([ensemble_predict(x) for x in X]) # 集成模型预测结果
ensemble_error = np.sum(ensemble_y_pred != y) / n_samples # 集成错误率
# 打印误差分析结果
print("\n" + "=" * 70)
print("误差分析结果")
print("=" * 70)
print(f"各弱分类器在原数据集上的错误率:{[round(e, 2) for e in weak_test_errors]}")
print(f"弱分类器平均错误率:{np.mean(weak_test_errors):.2f}")
print(f"集成模型在原数据集上的错误率:{ensemble_error:.2f}")
print("=" * 70)
# ---------------------- 6. 可视化模块(直观展示Bagging效果) ----------------------
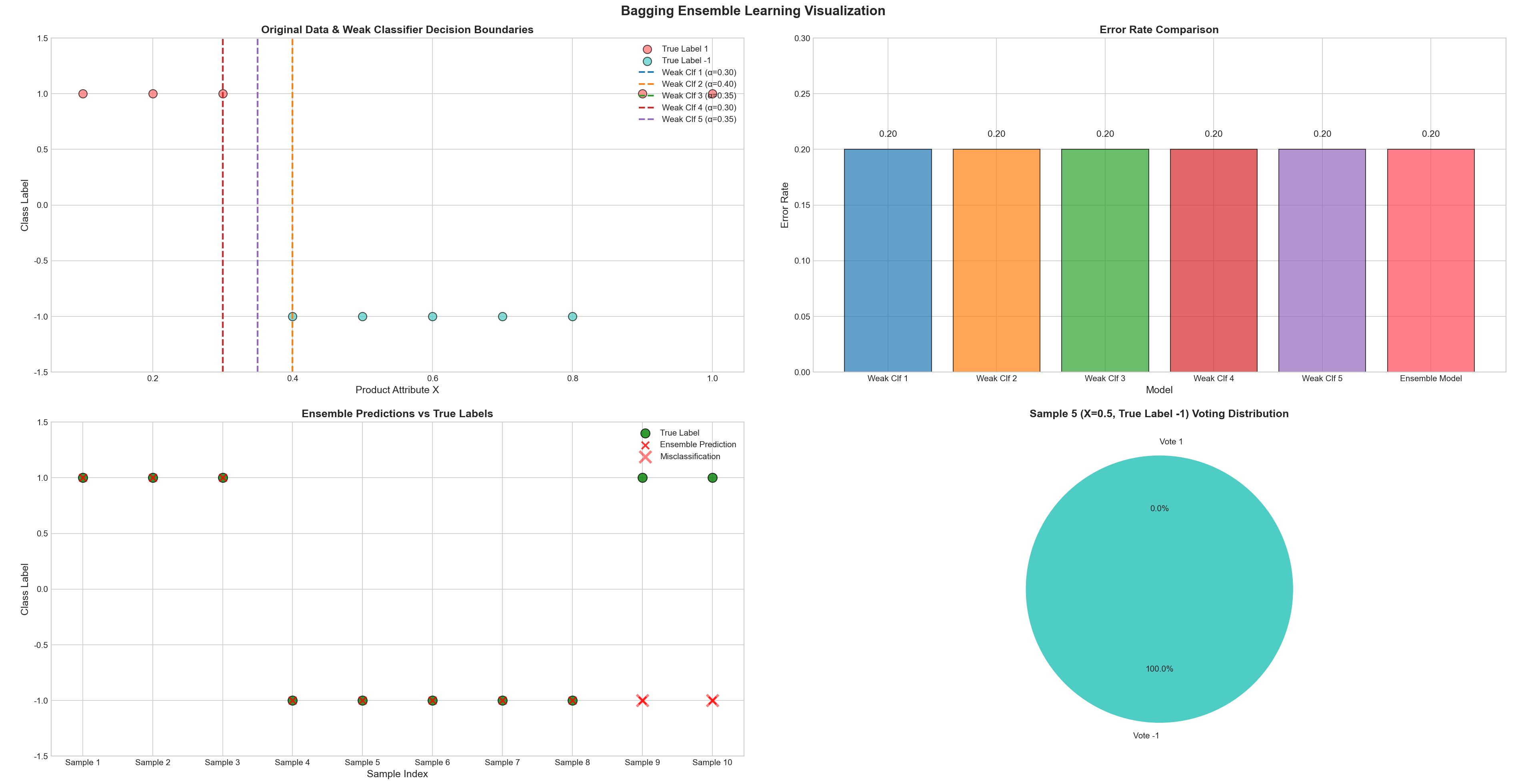
def plot_bagging_results():
"""
可视化内容:
1. 子图1:原始数据分布 + 所有弱分类器的决策边界
2. 子图2:弱分类器与集成模型的错误率对比
3. 子图3:集成模型预测结果与真实标签对比
4. 子图4:单个样本的弱分类器投票分布
"""
fig, axes = plt.subplots(2, 2, figsize=(15, 12)) # 2行2列子图布局
fig.suptitle('Bagging Ensemble Learning Visualization', fontsize=16, fontweight='bold')
# ---------------------- 子图1:原始数据 + 弱分类器决策边界 ----------------------
ax1 = axes[0, 0]
# 绘制原始数据点(按类别着色)
for cls in [1, -1]:
mask = y == cls
ax1.scatter(X[mask], [cls] * np.sum(mask), c=class_colors[cls],
s=100, label=f'True Label {cls}', alpha=0.7, edgecolors='black')
# 绘制每个弱分类器的决策边界(垂直直线x=α)
x_range = np.linspace(0.0, 1.1, 100) # X轴连续范围(用于画直线)
for i, alpha in enumerate(weak_alphas):
ax1.axvline(x=alpha, color=f'C{i}', linestyle='--', linewidth=2,
label=f'Weak Clf {i + 1} (α={alpha:.2f})')
# 图表美化
ax1.set_xlabel('Product Attribute X', fontsize=12)
ax1.set_ylabel('Class Label', fontsize=12)
ax1.set_title('Original Data & Weak Classifier Decision Boundaries',
fontsize=13, fontweight='bold')
ax1.legend(fontsize=10, loc='upper right')
ax1.set_ylim(-1.5, 1.5) # Y轴范围(避免标签超出)
# ---------------------- 子图2:错误率对比柱状图 ----------------------
ax2 = axes[0, 1]
# 数据准备
labels = [f'Weak Clf {i + 1}' for i in range(n_classifiers)] + ['Ensemble Model']
errors = weak_test_errors + [ensemble_error]
colors = [f'C{i}' for i in range(n_classifiers)] + ['#FF4757'] # 集成模型用红色突出
# 绘制柱状图(edgecolor单数兼容旧版本)
bars = ax2.bar(labels, errors, color=colors, alpha=0.7, edgecolor='black')
# 在柱子上标注错误率
for bar, err in zip(bars, errors):
height = bar.get_height()
ax2.text(bar.get_x() + bar.get_width() / 2., height + 0.01,
f'{err:.2f}', ha='center', va='bottom', fontsize=11)
# 图表美化
ax2.set_xlabel('Model', fontsize=12)
ax2.set_ylabel('Error Rate', fontsize=12)
ax2.set_title('Error Rate Comparison', fontsize=13, fontweight='bold')
ax2.set_ylim(0, max(errors) + 0.1) # Y轴范围(便于查看数值)
# ---------------------- 子图3:集成预测 vs 真实标签 ----------------------
ax3 = axes[1, 0]
# 绘制真实标签(绿色圆点)
x_pos = np.arange(n_samples) # X轴位置(样本索引)
ax3.scatter(x_pos, y, c='green', s=120, label='True Label', alpha=0.8, marker='o', edgecolors='black')
# 绘制集成模型预测标签(红色叉号)
ax3.scatter(x_pos, ensemble_y_pred, c='red', s=80, label='Ensemble Prediction',
alpha=0.8, marker='x', linewidth=2)
# 标注错误预测的样本(红色大叉号)
error_mask = ensemble_y_pred != y
ax3.scatter(x_pos[error_mask], ensemble_y_pred[error_mask], c='red', s=200,
alpha=0.5, marker='x', linewidth=3, label='Misclassification')
# 图表美化
ax3.set_xlabel('Sample Index', fontsize=12)
ax3.set_ylabel('Class Label', fontsize=12)
ax3.set_title('Ensemble Predictions vs True Labels',
fontsize=13, fontweight='bold')
ax3.set_xticks(x_pos)
ax3.set_xticklabels([f'Sample {i + 1}' for i in range(n_samples)])
ax3.legend(fontsize=10)
ax3.set_ylim(-1.5, 1.5)
# ---------------------- 子图4:单个样本的投票分布饼图 ----------------------
ax4 = axes[1, 1]
# 选择样本5(索引4,X=0.5)展示投票过程
sample_idx = 4
sample_x = X[sample_idx]
sample_true_y = y[sample_idx]
# 计算每个弱分类器对该样本的投票
votes = [h(sample_x) for h in weak_classifiers]
vote_counts = {1: votes.count(1), -1: votes.count(-1)}
# 绘制饼图
wedges, texts, autotexts = ax4.pie(vote_counts.values(), labels=[f'Vote {cls}' for cls in vote_counts.keys()],
colors=[class_colors[cls] for cls in vote_counts.keys()],
autopct='%1.1f%%', startangle=90)
# 图表美化
ax4.set_title(f'Sample {sample_idx + 1} (X={sample_x:.1f}, True Label {sample_true_y}) Voting Distribution',
fontsize=13, fontweight='bold')
# 调整子图间距(避免标签重叠)
plt.tight_layout()
# 保存图片(可选,取消注释即可保存高清图)
# plt.savefig('bagging_visualization.png', dpi=300, bbox_inches='tight', facecolor='white')
# 显示图片
plt.show()
# 调用可视化函数
plot_bagging_results()运行结果
======================================================================
Bagging集成学习 - 弱分类器训练过程
======================================================================
弱分类器1:阈值α=0.35 | 子数据集错误率=0.10 | 抽样索引=[4, 7, 8, 5, 0, 1, 7, 4, 5, 1]
弱分类器2:阈值α=0.35 | 子数据集错误率=0.30 | 抽样索引=[2, 2, 5, 8, 3, 8, 5, 4, 9, 7]
弱分类器3:阈值α=0.35 | 子数据集错误率=0.20 | 抽样索引=[0, 5, 4, 7, 3, 8, 3, 6, 9, 2]
弱分类器4:阈值α=0.30 | 子数据集错误率=0.20 | 抽样索引=[5, 0, 4, 3, 3, 0, 9, 1, 9, 7]
弱分类器5:阈值α=0.35 | 子数据集错误率=0.10 | 抽样索引=[1, 2, 4, 4, 3, 0, 8, 3, 2, 0]
======================================================================
误差分析结果
======================================================================
各弱分类器在原数据集上的错误率:[0.2, 0.2, 0.2, 0.2, 0.2]
弱分类器平均错误率:0.20
集成模型在原数据集上的错误率:0.20
======================================================================
Process finished with exit code 0
8.2.2 随机森林模型结构
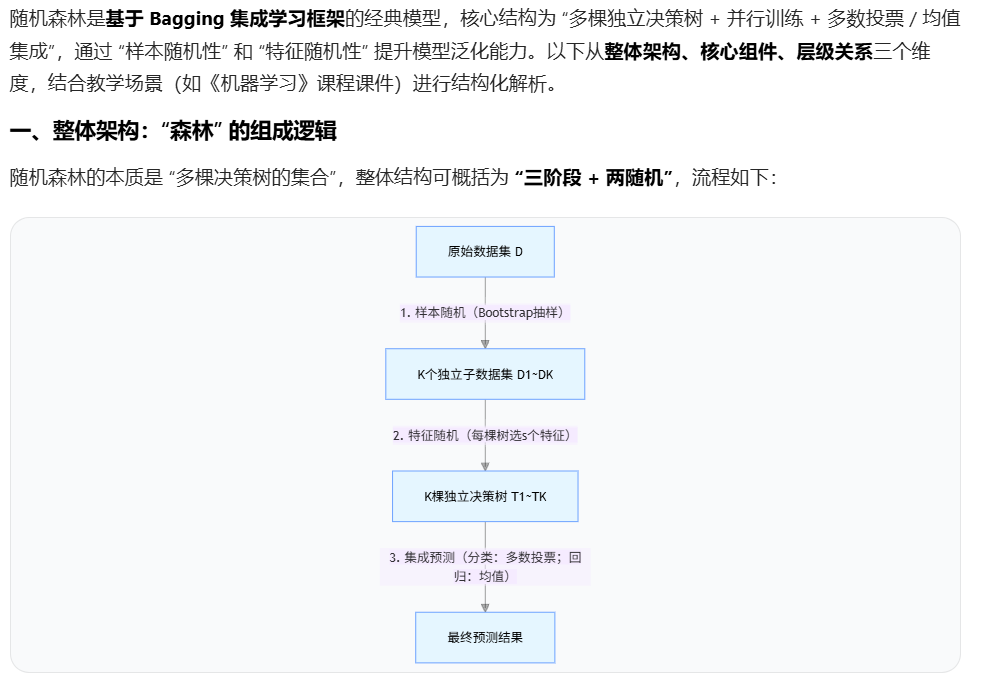
核心特点:
- 并行性:所有决策树独立训练,无依赖关系,可并行计算;
- 随机性:通过 "样本抽样" 和 "特征选择" 的双重随机,降低单棵树的相关性;
- 鲁棒性:单棵树过拟合可通过集成抵消,模型抗噪声能力强

决策树是一类简单有效的常用监督学习模型,可用Bagging集成学习方法将多个决策树模型作为弱学习器集成起来,构建一个较强泛化性能的森林模型作为强学习器。称由这些决策树作为弱学习器组合而成的森林模型为随机森林模型,通常简称为随机森林。
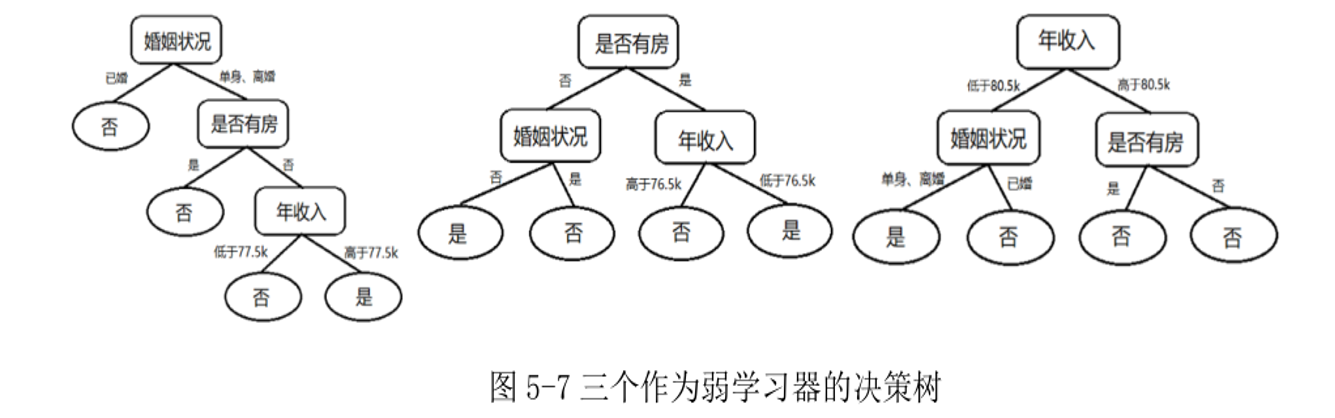
图 5-7 表示由某个贷款数据集通过随机性自助采样方式构造而成三个决策树模型。这三个决策树模型的结构有一定差异,对新客户是否会拖欠贷款的预测也有所不同。
可用相对多数投票法将这三个决策树模型作为弱学习器进行集成,构建一个如图 5-8 所示具有更高预测性能的随机森林模型。
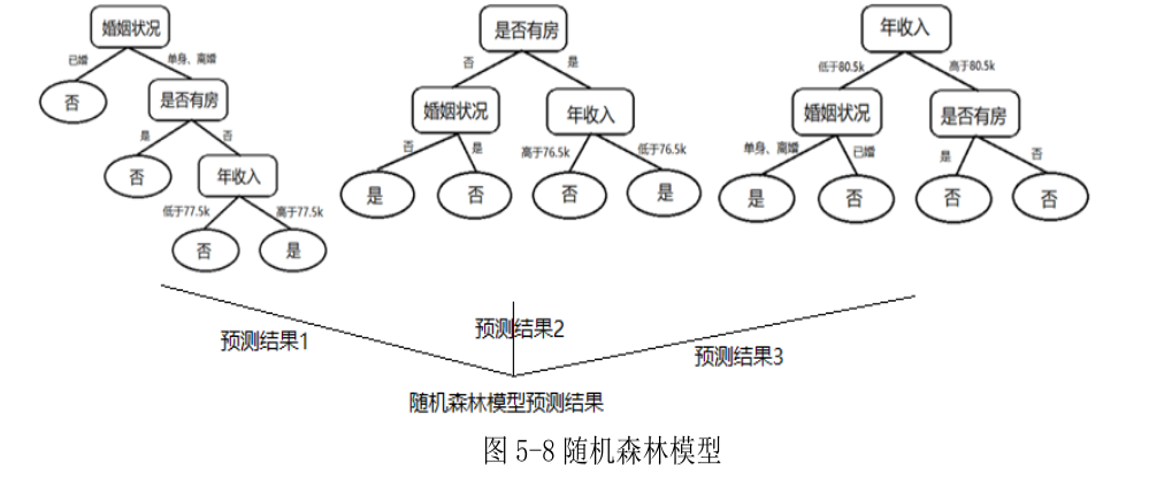
例如,对于输入样本X={婚姻状况=单身,是否有房=有,年收入=67.2k},图5-8所示随机森林模型对该样本的预测输出应为"是",表示该客户可能会拖欠贷款。这是由于尽管图5-8中最左侧决策树对该样本的预测值为"否",但其它两棵决策树对该样本的预测值均为"是",故根据相对多数投票法可得随机森林模型的预测输出为"是"。随机森林模型在Bagging集成策略基础上进一步增加了弱学习器之间的差异性,这使得随机森林模型能有效解决许多实际问题。
8.2.3 随机森林训练算法
随机森林模型基于 Bagging 集成学习方法构建,故训练构造随机森林模型过程基本上遵从 Bagging 集成学习的基本流程。具体地说,对于一个包含n个样本的数据集D,首先对D做k次随机性自助采样𝑙个训练样本子集D_1,D_2,⋯,D_k ,然后分别由D_1,D_2,⋯,D_k训练构造k棵决策树并这些决策树进行组合便可得到随机森林模型。

例题5.3
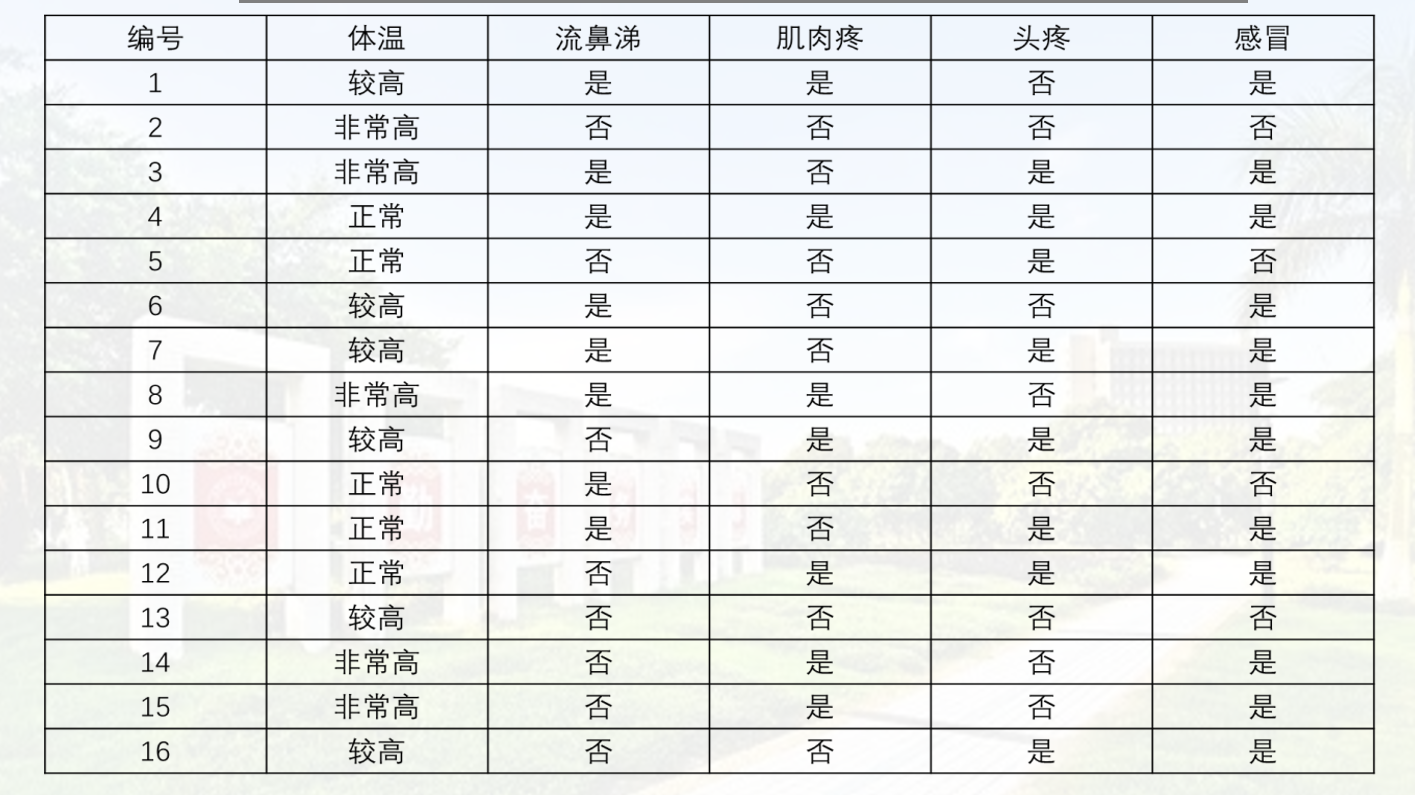
【例题5.3】表 5-6 是一个感冒诊断样本数据集,试用该数据集构造一颗作为随机森林弱学习器的 CART 决策树,在确定某结点的划分属性时,若该结点所对应属性集合具有m个特征,则规定从中随机选择s=⌈log_2m⌉个属性计算用于确定划分属性的基尼指数。


代码实现
8.3 Boosting集成学习