一、微分方程的直观理解------从生长曲线开始
1. 引言
假设我们有一个物体的数量N(t),它随时间 t变化。微分方程就是用未知函数与其导数(变化率)之间的关系来描述这个过程。
直观上,导数表示单位时间内数量变化的速度。
如果我们知道变化速度 怎么依赖于当前数量N(t),就可以写出微分方程。
2. 指数增长模型(最简单的生长曲线)
假设增长速度与当前数量成正比:
其中,r > 0是增长率。
意思:数量越大,增长越快(比如细菌繁殖)。
这是一个一阶线性微分方程。
解法:
两边积分:
即:,其中
是初始数量。
特点:
随时间指数增长,没有限制。
曲线是单调上升的"指数曲线"。
一般是自然条件下细菌、蓝藻,人为条件下营养充足的培养瓶里的果蝇

二、引入"环境容量K"限制------Logistic生长模型
1. 模型背景
真实生长往往不是无限制的,而是受环境资源限制。假设:
当数量较少时,增长接近指数增长。
当数量接近环境最大容量 K时,增长速度趋近于0。
用微分方程描述:
其中
r是增长率,
K是环境容量。
2.方程含义解析
N/K是环境容量比率,如果比率最大应该是1,表示剩余的环境容量比率,理解表达式较快的方法之一可以通过取极限:
当(环境容量),近似为1,即指数增长;
当,增长速度趋近于零,达到稳定状态。
3. 解法思路(变量可分离)
写成:
分离变量:
利用分式分解:
所以
中间过程就省略了,最终整理得标准逻辑斯蒂方程解:
其中 。
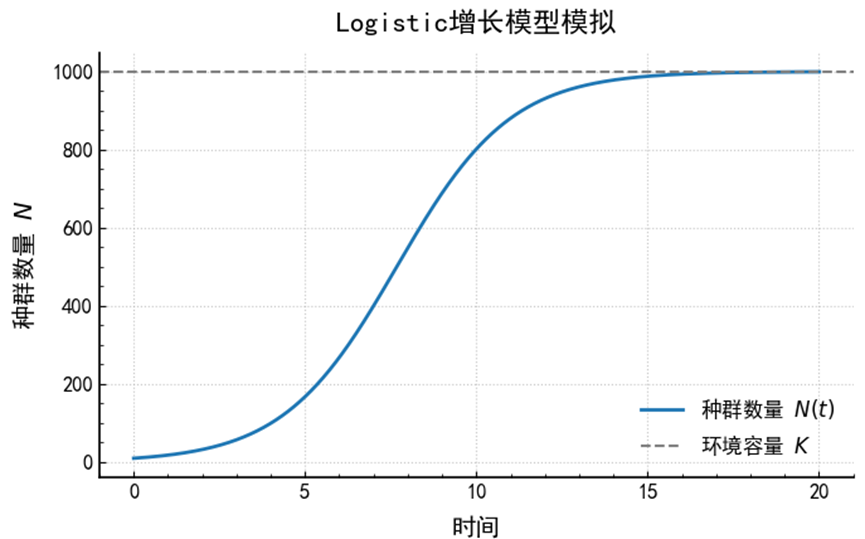
4. 曲线特征
S型曲线(sigmoid),先近似指数增长,
中期斜率最大(增长最快),
后期趋近稳定容量K。
****改进:****具体问题中引入更多的限制
1. 引入环境扰动与周期性变化
例如:周期性环境因子:季节之类的变化
增长率随时间变化,模拟季节或周期性环境影响。
2. 引入个体差异与结构
例如: 年龄结构/阶段结构
用分组或连续变量描述不同年龄/阶段的种群,常见如Leslie矩阵或偏微分方程,但本质上是将Logistic中的N拆解为多个分组(如 ),每组有不同的生存与繁殖率。
三、从N → N1,N2:两个物种------竞争与捕食模型(Lotka-Volterra)
两个物种最常见的两种关系是竞争与捕食,下面通过经典的Lotka-Volterra方程组来分析两种关系。
1. 竞争模型
假设两个物种竞争资源,数量分别为N1,N2,变成两个之后,
情况立马就复杂不少了,我们要考虑:对方种群(N2)对自身(N1)的影响
所以不妨定义:α,β是竞争系数,表示对方种群对自身的影响。
并且两个物种各自之间的各自的环境最大容量(资源极限)也不一样,我们定义为K1,K2
方程组:
两个方程耦合,描述种群动态的相互作用。
参数含义:
r1,r2:第1、第2种群的内在增长率,
K1,K2:各自的环境最大容量(资源极限),
α :种群2对种群1的"竞争系数",表示1单位的种群2对种群1的影响相当于多少单位的种群1自己,
β:种群1对种群2的竞争系数。
单独看N1的增长项:是逻辑斯蒂增长,表示种群1如果没有竞争者,增长会趋向K1。
αN2表示竞争的"压力":种群2越多,种群1生存空间越小。
同理对另一个种群。
共存:两种群都稳定存在(相互影响但均有足够资源)。
竞争排斥:一个种群优势,挤压另一个种群直到灭绝。
不稳定平衡:种群数量敏感,轻微变化导致一方灭绝。
平衡点:设,
,求解平衡点(定态): 可能有零种群、单一物种存活、或两种共存的平衡。
线性化稳定性分析:计算雅可比矩阵在平衡点的特征值,判断系统稳定性。 -
相平面分析:绘制N1与N2的轨迹,观察动态变化趋势。
2. 捕食-被捕食模型(Lotka-Volterra模型)
这个模型又可以用来描述捕食和被捕食
先举个具体例子:狼和鹿
狼和鹿在同一片草原上共存,会出现以下几个阶段:
1.猎物充足,捕食者开始受益
一开始,草原上鹿很多,因为草多,食物充足,鹿数量稳步增长。对于狼来说,鹿多的话,捕猎很容易成功。那么狼数量也增加。
2.捕食者过多,猎物被大量捕食
随着狼越来越多,它捕食的鹿也越来越多。鹿的死亡率上升,增长速度变慢,并开始下降。此时,鹿的总数达到了一个峰值后开始减少。
3.猎物短缺,捕食者陷入困境
由于鹿的数量已经被压得很低,狼群发现捕猎变得异常困难,经常饿肚子。没吃的数量肯定变低,因为食物短缺导致狼的幼崽存活率下降,成年狼也可能饿死或体质变弱,狼的种群数量开始急剧下降。
4.捕食者减少,猎物得到喘息
随着狼的数量减少到很低水平,对驯鹿的捕食压力大大减轻。幸存下来的驯鹿获得了宝贵的喘息机会,它们会迅速繁殖,种群数量又开始回升。
下面通过列方程组来描述一下以下过程:
假设捕食者为P(t),被捕食者为N(t),它们的关系:
其中
r :被捕食者的自然增长率(无捕食时增长),
a :捕食率(被捕食者减少速度),被捕食者死亡率与捕食者数量的乘积比例系数
m :捕食者的自然死亡率(无猎物时死亡),
b:捕食者因捕食增加的增长率。
方程解读:
: rN:猎物自然繁殖,-aNP :被捕食者被捕杀减少。
:-mP:捕食者自然死亡,bNP:捕食者因猎物增加而增长。
意义:
捕食者和被捕食者数量通常会出现周期性波动,
被捕食者多时,捕食者因食物充足数量增加;
捕食者多导致猎物减少,继而捕食者饥饿数量减少;
形成"振荡"现象。
平衡点:解得:
即平衡点在处。
四、从固定的K → 动态的R(t):资源---消费者模型(Monod)
在前面讲的所有种群模型中,资源限制全是固定的参数,Logistic 模型中的承载容量 K、Lotka(洛特卡)-Volterra 竞争模型中的K1、K2,本质上都是将真实资源(食物、水、空间等)简化成了常数。这种处理虽然模型假设上简洁,却无法反映真实的资源再生与消耗过程。 在真实的自然生态系统中,资源是动态的:比如草被吃掉一点,雨水会再冲进来一点,植物死亡后又会分解一点......被消费者摄取后,可通过外界输入、生物再生或化学循环得到补充。因此,有必要将资源浓度作为独立的动态变量R(t)引入模型。
莫诺方程原来是描述蓝藻的,我们不按照蓝藻的比喻,因为具体建模问题中大概率遇不到这种细菌、真菌的题,我们举个动物的例子,设定越简洁越好理解,就举羊和草的例子,由logistic的基本形式开始推导,再看在这个基础上是怎么改的
在之前的Logistic、Lotka-Volterra等模型中,资源限制都是固定的常数(比如承载容量K),相当于假设"草量永远是某个固定值"。但现实草原上,草不是静止的:被羊吃掉一部分后,阳光、雨水、土壤养分会让草不断重新生长。因此,我们必须把草本身也当作一个会变化的动态变量。
记Kg:草自身的承载容量,表示"没有羊时草自己能长到的最大量"。
没有羊时候的草,按照logistic的写法,把物种数量N(t)换成环境容量R(t):
平衡时 dR/dt = 0 → R(1−R/Kg) = 0 → R* = Kg→ 没有羊时,草最终稳定在Kg
然后,有羊之后,就得减掉羊吃的草了
理解过程:


是饱和函数,质量比最大摄食速率,单位:(资源质量)/(消费者质量·时间),
R → 0 时,μ(R) ≈ R/K_s → 0
- 当R → ∞ 时,μ(R) → 1
- 当R = Ks 时,μ(R) = 1/2
这个Ks的含义:
资源必须保持R > Ks才能让消费者种群持续增长,否则崩溃
如果放牧把草压到 < Ks,羊群第二年必然大幅下降
所以上述第一个表达式是
第二个式子:
其中e是草→羊转化效率,羊吃的草*e = 转化成羊增长的数量,只有按照e这个比例的真正转化为羊的生物量(剩下的是呼吸、粪便等损失)
d 是正常死亡率 ,整个式子就是:羊的数量增长 = 吃草转化羊的速率 -- 羊自然死亡的速率
上述三个重要方程组的讲解视频如下:(如果觉得视频有用,跪求三连)