代码随想录算法训练营Day33 | 322.零钱兑换、279.完全平方数、139.单词拆分、背包总结

LeetCode322.零钱兑换

322. 零钱兑换 - 力扣（LeetCode）

1.思路

动态规划五部曲：

dp[j]：凑足总额为 j 的所需钱币的最少个数；
凑足总额为 j - coins[i] 的最少个数为 dp[j - coins[i]]，那么只需要加上一个钱币 coins[i]，即 dp[j - coins[i]] + 1，最后取所有 dp[j - coins[i]] + 1 中最小的数。

递推公式：dp[j] = min(dp[j]，dp[j - coins[i]] + 1)；

dp[0] = 0，凑足总额为 0 的钱币个数一定为 0；其他数在初始化时初始化为最大值，防止求最小值时被覆盖；
本题钱币能无限使用，所以外层遍历物品，内层正向遍历背包；
coins = [1，2，5]，amount = 5

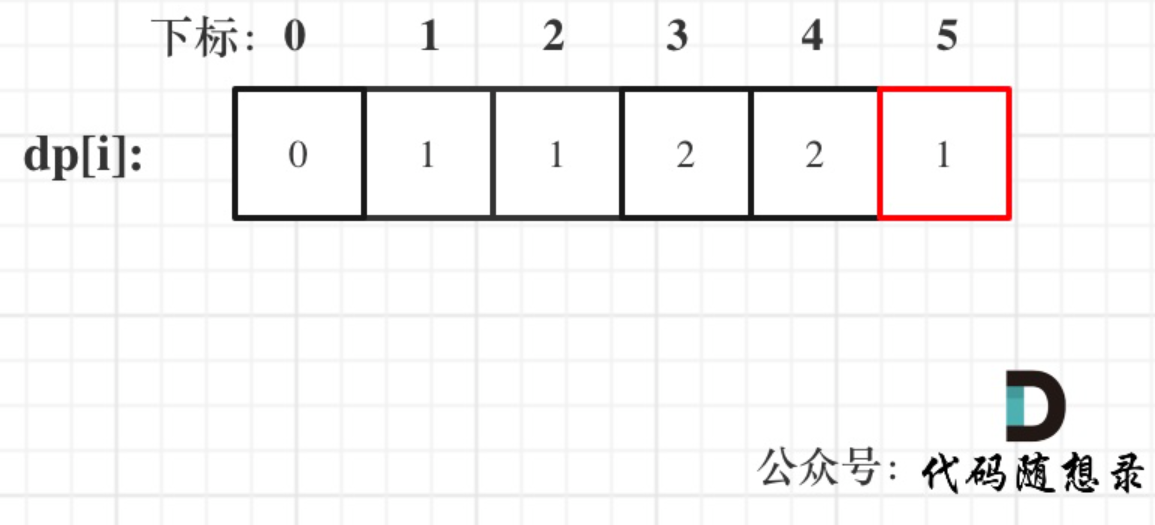
cpp 复制代码

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int>dp(amount+1,INT_MAX);
        dp[0]=0;
        for(int i=0;i<coins.size();i++){
            for(int j=coins[i];j<=amount;j++){
                if(dp[j-coins[i]] < INT_MAX-1){
                    dp[j]=min(dp[j],dp[j-coins[i]]+1);
                }
            }
        }
        return dp[amount]==INT_MAX ? -1:dp[amount];
    }
};

2.复杂度分析

时间复杂度：O(amount*n)

空间复杂度：O(amount)

3.思考

本题和零钱兑换II 不同，那道题求得是组合数，直接代用公式就能解决，而这道题则是求得是满足条件得最少硬币个数，所以递推公式也会相应地改变，也不再是原来反复使用的公式，而是需要在 dp[j - coins[i]] 的基础上再去一次 coins[i]，即 dp[j - coins[i]] + 1，也就得到了 dp[j]。

4.Reference：322. 零钱兑换 | 代码随想录

LeetCode279.完全平方数

279. 完全平方数 - 力扣（LeetCode）

1.思路

完全平方数就是物品（可以无限件使用），凑个正整数n就是背包，求凑满这个背包最少有多少物品。思路和上面的题一样。

动态规划五部曲：

和为 j 的完全平方数的最少数量；
在 dp[j - i*i] 的基础上加上 i*i，即 dp[j - i*i] +1 便能得到 dp[j]，最后选择最小的 dp[j] 即可；

递推公式：dp[j] = min(dp[j]，dp[j - i*i] + 1)；

dp[0] = 0，n 从 1 开始，所以 0 的完全平方数为 0，其他数初始化为最大值，防止被覆盖；
这道题和上一道题一样都是求最小值，所以先遍历物品再遍历背包，还是交换一下都是可以的，不过物品可以重复使用，所以背包一定要正向遍历；
n = 5

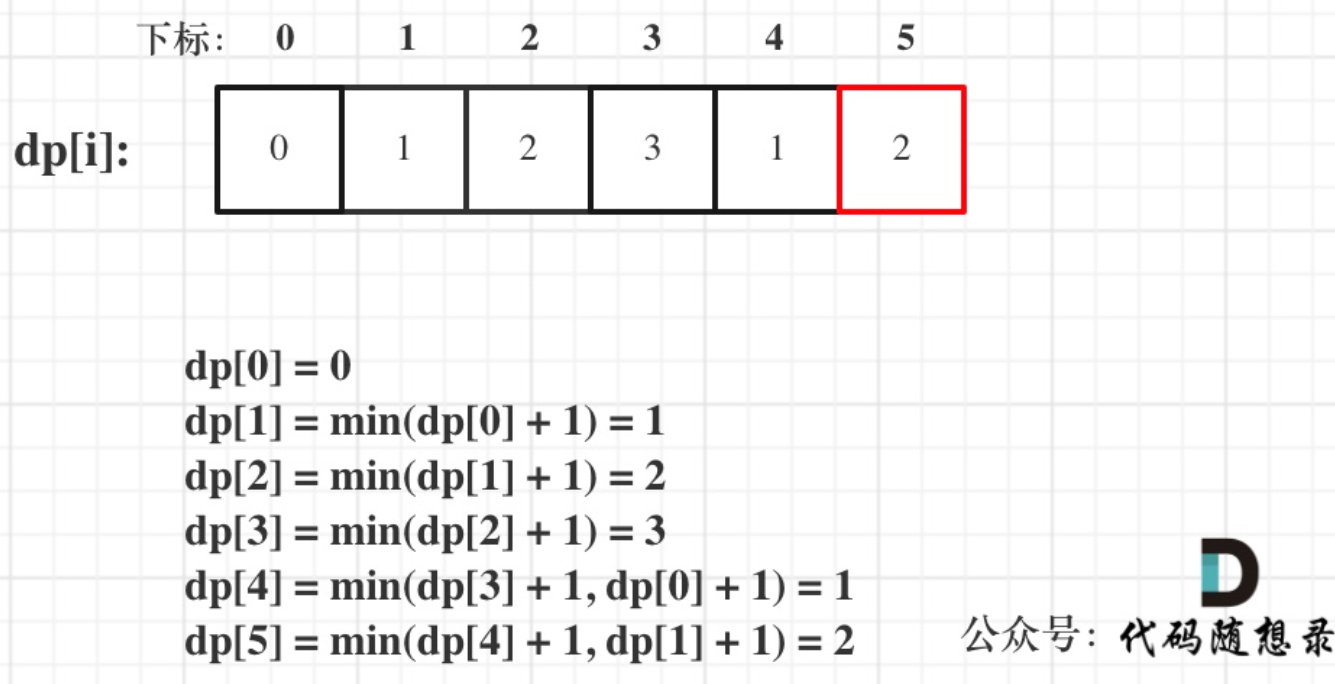
cpp 复制代码

class Solution {
public:
    int numSquares(int n) {
        vector<int>dp(n+1,INT_MAX);
        dp[0]=0;
        for(int i=1;i*i<=n;i++){
            for(int j=i*i;j<=n;j++){
                if(dp[j-i*i]<INT_MAX-1){
                   dp[j]=min(dp[j],dp[j-i*i]+1); 
                }
            }
        }
        return dp[n];
    }
};

2.复杂度分析

时间复杂度：O(n * √n)

空间复杂度：O(n)

3.思考

求最小值的问题，递推公式不能依赖之前的模板，dp[j] = min(dp[j]，dp[j - nums[i]] + 1)，这里就需要求满足条件的最小值，所以在初始化的时候就要初始化为最大值，防止被覆盖。

4.Reference：279.完全平方数 | 代码随想录

LeetCode139.单词拆分

139. 单词拆分 - 力扣（LeetCode）

1.思路

单词就是物品，字符串s就是背包，单词能否组成字符串s，就是问物品能不能把背包装满。

拆分时可以重复使用字典中的单词，说明就是一个完全背包。

动态规划五部曲：

dp[i]: 字符串长度为 i，dp[i] 为 true，表示可以拆分为一个或多个在字典中出现的单词；
如果 dp[j] = true，且 [j, i] 这个区间的子串出现在字典里，那么 dp[i] 一定是true。

递推公式：if ( [j, i] 这个区间的子串出现在字典里 && dp[j] = true)，那么 dp[i] = true；

dp[i] 初始化为 false，只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词。从递推公式中看出，dp[i] 的状态依赖 dp[j]，那么 dp[0]一定要为true，否则递推后面都是 false；
本题需要先遍历背包，后遍历物品，因为要组成字符串 s，单词间就必须按照顺序排列；
s = "leetcode"，wordDict = ["leet"，"code"]

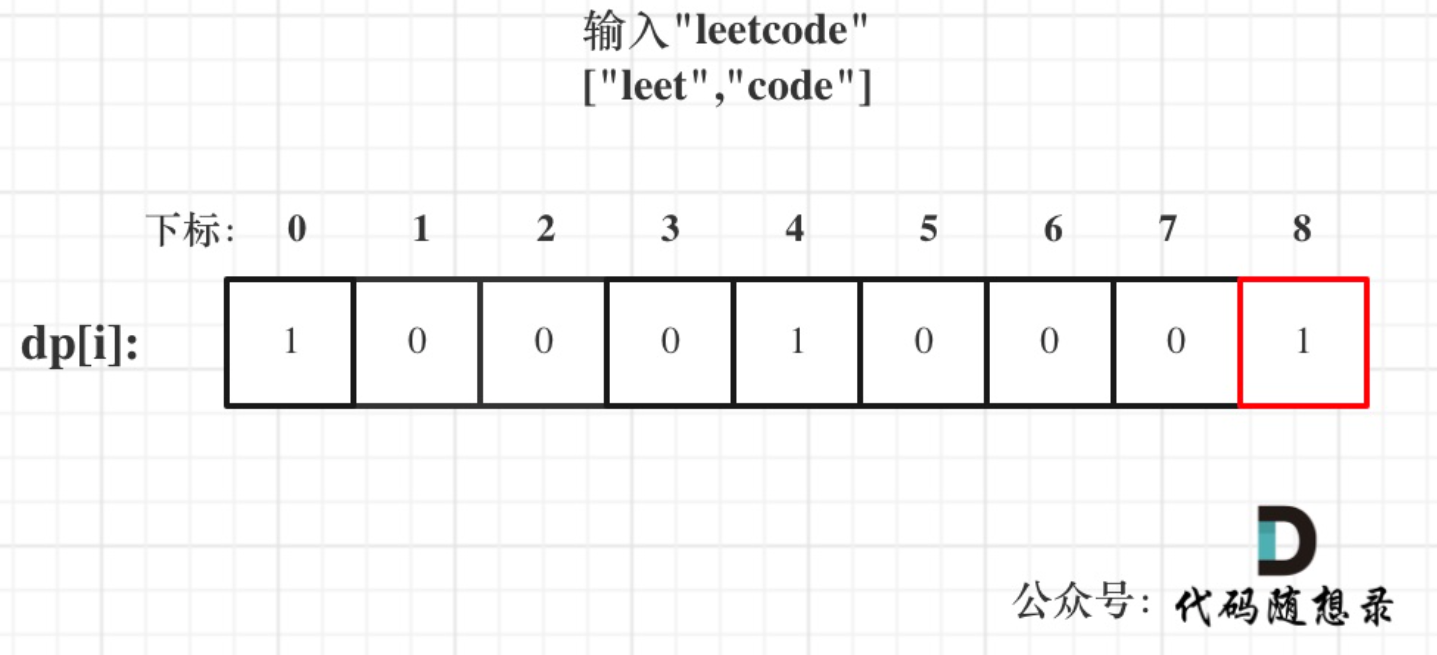
cpp 复制代码

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        vector<bool>dp(s.size()+1,false);
        dp[0]=true;
        set<string>st(wordDict.begin(),wordDict.end());
        for(int i=1;i<=s.size();i++){
            for(int j=0;j<i;j++){
                string word = s.substr(j,i-j);
                if(st.find(word)!=st.end() && dp[j]){
                    dp[i]=true;
                }
            }
        }
        return dp[s.size()];
    }
};

2.复杂度分析

时间复杂度：O(n^3)

空间复杂度：O(n)

3.思考

这道题难度很大，用回溯法还能做一做，背包的话是真的难想。

4.Reference：139.单词拆分 | 代码随想录

背包总结

一、递推公式

1. 能否装满背包 / 最多装多少

公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])

典型题目：416. 分割等和子集、1049. 最后一块石头的重量 II

2. 装满背包有几种方法

公式：dp[j] = dp[j] + dp[j - nums[i]]

典型题目：494. 目标和、518. 零钱兑换 II、377. 组合总和 Ⅳ、70. 爬楼梯进阶版（完全背包）

3. 背包装满的最大价值

公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

典型题目：474. 一和零

4. 装满背包的最小物品个数

公式：dp[j] = min(dp[j - coins[i]] + 1, dp[j])

典型题目：322. 零钱兑换、279. 完全平方数

二、遍历顺序

1. 01 背包（物品仅用一次）

（1）二维 dp 数组实现

遍历顺序：先遍历物品或先遍历背包容量均可

内层循环：从小到大遍历（j 从 0 到 bagSize）

（2）一维 dp 数组（滚动数组）实现

遍历顺序：必须先遍历物品，再遍历背包容量

内层循环：必须从大到小遍历（j 从 bagSize 到 weight [i]），避免物品重复使用

2. 完全背包（物品可重复使用）

（1）纯完全背包（求最大价值 / 能否装满）

遍历顺序：先遍历物品或先遍历背包容量均可

内层循环：从小到大遍历（j 从 weight [i] 到 bagSize）

（2）求组合数（不考虑顺序）

遍历顺序：外层 for 遍历物品，内层 for 遍历背包容量

典型题目：518. 零钱兑换 II

（3）求排列数（考虑顺序）

遍历顺序：外层 for 遍历背包容量，内层 for 遍历物品

典型题目：377. 组合总和 Ⅳ、70. 爬楼梯进阶版（完全背包）

（4）求最小物品个数

遍历顺序：两层 for 循环先后顺序无要求

典型题目：322. 零钱兑换、279. 完全平方数