前言
🔥个人主页:不会c嘎嘎
📚专栏传送门:【数据结构】 、【C++】 、【Linux】、【算法】、【MySQL】
🐶学习方向:C++方向学习爱好者
⭐人生格言:谨言慎行,戒骄戒躁
每日一鸡汤:
"别怕走得慢,只怕停下来。每一个不曾起舞的日子,都是对生命的辜负。你流下的每一滴汗水,都会在未来某个时刻开花结果。即使现在看不到希望,也要相信,黑夜再长,也挡不住黎明的光。坚持下去,不是因为看见了希望才努力,而是努力了,才能看见希望。"


目录
[1.1 什么是红黑树](#1.1 什么是红黑树)
[1.2 红黑树的性质](#1.2 红黑树的性质)
[4.1 情况一:cur 为红,p 为红,g 为黑,u 存在且为红](#4.1 情况一:cur 为红,p 为红,g 为黑,u 存在且为红)
[4.2 情况二:cur 为红,p 为红,g 为黑,u 不存在 或 u 为黑](#4.2 情况二:cur 为红,p 为红,g 为黑,u 不存在 或 u 为黑)
1.红黑树的概念
1.1 什么是红黑树
红黑树(Red-Black Tree),是一种二叉搜索树(BST)。但在每个节点上,它增加了一个存储位来标识节点的颜色,该颜色可以是 Red 或 Black。
通过对任何一条从根到叶子的路径上的各个节点着色方式的限制,红黑树能够确保没有一条路径会比其他路径长出两倍 ,因而是近似平衡的。
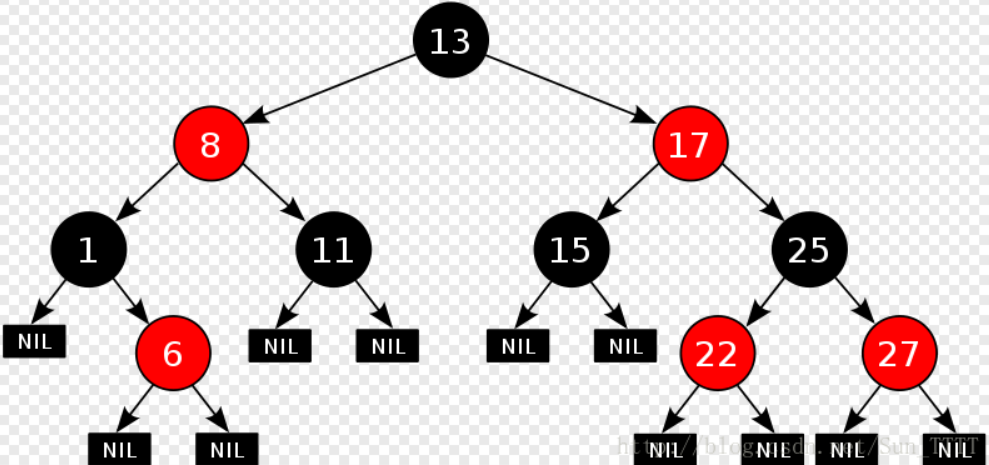
1.2 红黑树的性质
红黑树的强大之处在于它严格遵循以下规则。一旦在插入或删除后破坏了这些规则,就需要通过变色或旋转来恢复。
节点颜色:每个节点不是黑色就是红色。
根节点:根节点必须是黑色的。
红色规则:如果一个节点是红色的,那么它的两个孩子节点必须是黑色的(即:路径上不能出现连续的两个红色节点)。
黑色规则:对于任意一个节点,从该节点到其所有后代叶子节点的简单路径上,均包含相同数量的黑色节点。
2.红黑树节点的定义
红黑树的底层实现通常与 AVL 树类似,使用三叉链结构(包含指向父节点的指针),以便于进行旋转和回溯更新。
cpp
enum Col {
RED,
BLACK
};
template <class K, class V>
struct RBTreeNode
{
typedef RBTreeNode<K, V> Node;
std::pair<K, V> _kv;
Node *_left;
Node *_right;
Node *_parent;
Col _col;
RBTreeNode(const std::pair<K, V> &kv = std::pair<K, V>(), Col col = RED)
: _kv(kv),
_left(nullptr),
_right(nullptr),
_parent(nullptr),
_col(col) // 默认颜色为红色
{
}
};;2.1为什么默认插入的节点是红色的?
这是一个非常关键的设计细节。
如果插入黑色节点 :必然会改变某条路径上的黑色节点数量,从而违反性质 4。这意味着所有其他路径都需要调整,代价极大。
如果插入红色节点 :可能会违反性质 3(出现连续红节点),但这只影响当前子树,通过变色或旋转通常更容易修复。
因此,默认插入红色节点是为了尽可能减少对红黑树规则的破坏,降低调整成本
3.红黑树的插入
红黑树的插入流程可以分为两步:
BST 插入:按照二叉搜索树的规则找到位置并插入新节点。
调整平衡:如果插入后违反了红黑树性质(主要是出现连续红节点),则需要向上更新颜色或进行旋转
cpp
bool Insert(const std::pair<K, V>& kv)
{
// 1. 空树特判
if (_root == nullptr)
{
_root = new Node(kv, BLACK); // 根节点必须是黑色
return true;
}
Node* parent = nullptr;
Node* cur = _root;
// 2. 寻找插入位置
while (cur)
{
if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
return false; // key 已经存在
}
}
// 3. 插入新节点
cur = new Node(kv, RED); // 新节点默认为红
if (parent->_kv.first > kv.first)
parent->_left = cur;
else
parent->_right = cur;
cur->_parent = parent;
// 4. 开始调整颜色或旋转...
// (接下文的调整逻辑)
return true;
}4.红黑树的旋转与变色
插入完成后,如果父节点 parent 是红色的,就违反了性质 3(不能有连续红节点),此时需要根据叔叔节点(Uncle)的情况进行处理。
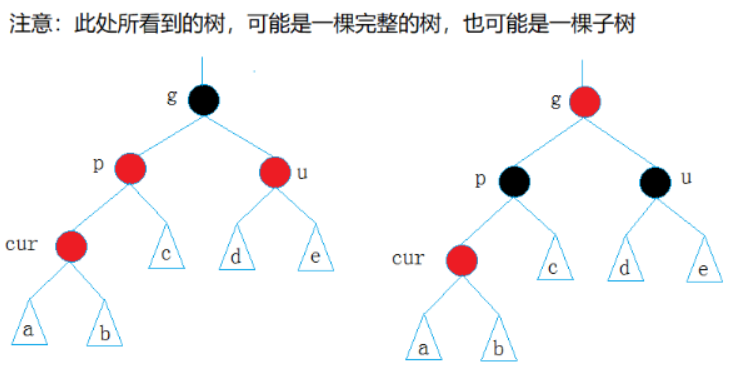
4.1 情况一:cur 为红,p 为红,g 为黑,u 存在且为红
这是最简单的情况。既然 p 和 u 都是红色,我们可以通过变色来解决冲突,并将黑色向上传递。
操作 :将
p和u变为黑色,将g变为红色。后续 :如果
g是根节点,需将其改回黑色;如果g的父节点也是红色,则需要继续向上调整。
cpp
// 伪代码逻辑
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
gparent->_col = RED;
// 继续向上调整
cur = gparent;
parent = cur->_parent;
}4.2 情况二:cur 为红,p 为红,g 为黑,u 不存在 或 u 为黑
当叔叔节点不存在,或者叔叔节点是黑色时,单纯的变色无法解决问题(会导致黑色节点数量不一致),必须进行旋转。
旋转又分为两种子情况(假设 p 是 g 的左孩子):
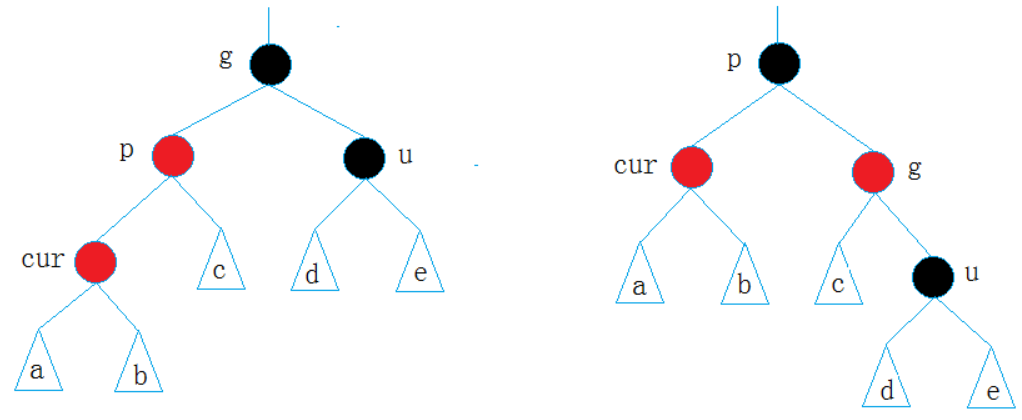
单旋(LL型) :
cur是p的左孩子。
操作 :对
g进行右单旋。变色 :
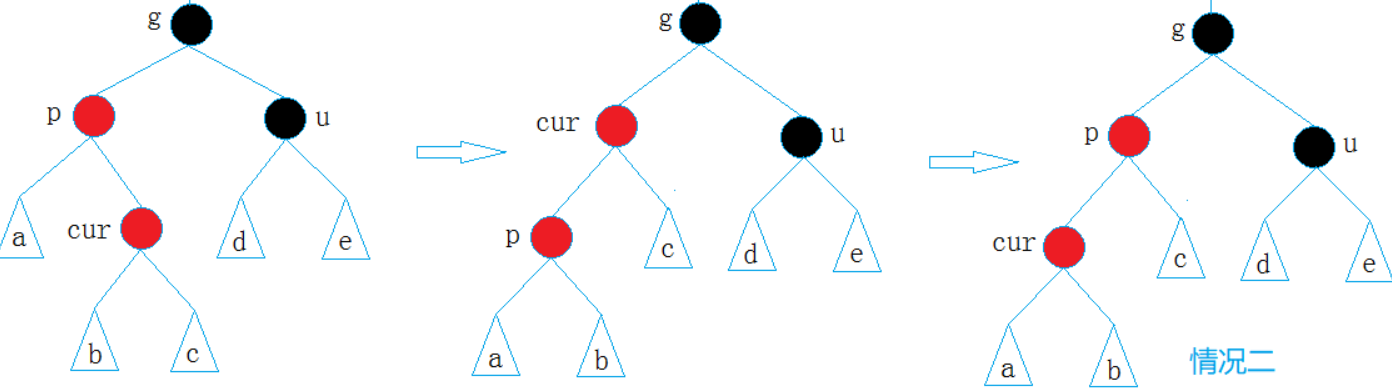
p变黑,g变红。双旋(LR型) :
cur是p的右孩子。
操作 :先对
p进行左单旋 (变成 LL 型),再对g进行右单旋。变色 :
cur(最终的根)变黑,g变红。
单旋(LL型) :cur 是 p 的左孩子。
双旋(LR型) :cur 是 p 的右孩子。
cpp
// 插入后的调整逻辑
while (parent && parent->_col == RED)
{
Node *gparent = parent->_parent;
// ============================
// A. 父亲是爷爷的左孩子
// ============================
if (parent == gparent->_left)
{
Node *uncle = gparent->_right;
// --- 情况 1:叔叔存在且为红 ---
// 策略:变色 + 向上继续调整
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
gparent->_col = RED;
// 向上更新
cur = gparent;
parent = cur->_parent;
}
else
{
// --- 情况 2:叔叔不存在 或 叔叔为黑 ---
// 2.1 LL型:cur是左孩子 -> 右单旋
// g
// p u
// c
if (cur == parent->_left)
{
_RotateR(gparent);
parent->_col = BLACK;
gparent->_col = RED;
}
// 2.2 LR型:cur是右孩子 -> 左右双旋
// g
// p u
// c
else
{
_RotateL(parent);
_RotateR(gparent);
cur->_col = BLACK;
gparent->_col = RED;
}
break; // 旋转后子树根变黑,无需继续向上
}
}
// ============================
// B. 父亲是爷爷的右孩子 (与上面对称)
// ============================
else
{
Node *uncle = gparent->_left;
// --- 情况 1:叔叔存在且为红 ---
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
gparent->_col = RED;
cur = gparent;
parent = cur->_parent;
}
else
{
// --- 情况 2:叔叔不存在 或 叔叔为黑 ---
// 2.1 RR型:cur是右孩子 -> 左单旋
if (cur == parent->_right)
{
_RotateL(gparent);
parent->_col = BLACK;
gparent->_col = RED;
}
// 2.2 RL型:cur是左孩子 -> 右左双旋
else
{
_RotateR(parent);
_RotateL(gparent);
cur->_col = BLACK;
gparent->_col = RED;
}
break;
}
}
}
// 根节点永远保持黑色
_root->_col = BLACK;5.红黑树的性能
红黑树和 AVL 树都是高效的平衡二叉树,但它们的侧重点有所不同:
时间复杂度:
- 红黑树确保存储 N个节点的树的高度为 O(\log N),因此其查找、插入、删除操作的时间复杂度均为 O(log N)。
与 AVL 树的对比:
AVL 树是严格平衡的(高度差不超过 1),查找效率极高,但在插入和删除时需要频繁旋转,维护成本较高。
红黑树 是近似平衡的(最长路径不超过最短路径的 2 倍),它通过降低对平衡性的要求,换取了更少的旋转次数。
应用场景:
- 由于红黑树在插入和删除时的综合性能更优,实际应用中比 AVL 树更广泛。例如:C++ STL 中的
map和set、Java 中的TreeMap以及 Linux 内核中的虚拟内存管理等,底层都使用了红黑树。
结语
通过本文,我们详细解析了红黑树的四大性质 、节点定义 以及最核心的插入调整逻辑。
我们看到,红黑树的精髓在于:默认插入红色节点 以减少对全局规则的破坏,并通过局部性的变色 和旋转(左旋、右旋)来快速修复平衡。正是这种精妙的机制,保证了红黑树在最坏情况下的时间复杂度依然维持在 O(log N)。
掌握红黑树不仅是为了应付面试,更是为了深入理解 STL 容器背后的实现原理。接下来的学习中,你可以尝试思考红黑树的删除操作 ,或者试着封装一个简易版的 MyMap 和 MySet,进一步巩固所学知识。
以上就是本期博客的全部内容,感谢各位的阅读以及观看。如果内容有误请大佬们多多指教,一定积极改进,加以学习。
