INT301 Bio-computation 生物计算（神经网络）Pt.9 自我组织特征映射（Self-Organizing Fearure Map）

文章目录

[1. 自我组织映射（Self-Organizing Map， SOM）](#1. 自我组织映射（Self-Organizing Map， SOM）)
[2. 特征映射（Feature Maps）](#2. 特征映射（Feature Maps）)
- [2.1 拓扑图（Topographic Maps）](#2.1 拓扑图（Topographic Maps）)
- - [2.1.1 拓扑图的生成机制](#2.1.1 拓扑图的生成机制)
  - [2.1.2 自组织映射（Self-Organizing Map，SOM）](#2.1.2 自组织映射（Self-Organizing Map，SOM）)
  - - [2.1.2.1 SOM算法的过程](#2.1.2.1 SOM算法的过程)
    - - [2.1.2.1.1 初始化（Initialization）](#2.1.2.1.1 初始化（Initialization）)
      - [2.1.2.1.2 竞争过程](#2.1.2.1.2 竞争过程)
      - [2.1.2.1.3 合作过程](#2.1.2.1.3 合作过程)
      - [2.1.2.1.3.1 邻域（neighborhood）](#2.1.2.1.3.1 邻域（neighborhood）)
      - [2.1.2.1.4 适应过程](#2.1.2.1.4 适应过程)
      - [2.1.2.1.4.1 学习率（Learning Rate）](#2.1.2.1.4.1 学习率（Learning Rate）)
    - [2.1.2.2 SOM算法的训练流程](#2.1.2.2 SOM算法的训练流程)
    - [2.1.2.3 SOM算法的特性](#2.1.2.3 SOM算法的特性)
[3. 学习向量量化器（Learning Vector Quantizer，LVQ）](#3. 学习向量量化器（Learning Vector Quantizer，LVQ）)
- [3.1 简单竞争学习（Simple Competitive Learning）](#3.1 简单竞争学习（Simple Competitive Learning）)
- [3.2 向量量化（Vector Quantization）](#3.2 向量量化（Vector Quantization）)
- [3.3 学习向量量化器（Learning Vector Quantizer，LVQ）](#3.3 学习向量量化器（Learning Vector Quantizer，LVQ）)
- - [3.3.1 LVQ1](#3.3.1 LVQ1)
  - [3.3.2 LVQ2](#3.3.2 LVQ2)
- [3.4 小结](#3.4 小结)

1. 自我组织映射（Self-Organizing Map， SOM）

大脑是一个自我组织系统。这意味着大脑能够通过改变神经元之间的连接（增加、删除、加强）来自我学习和调整。

具有相似功能的神经元被分组在一起。

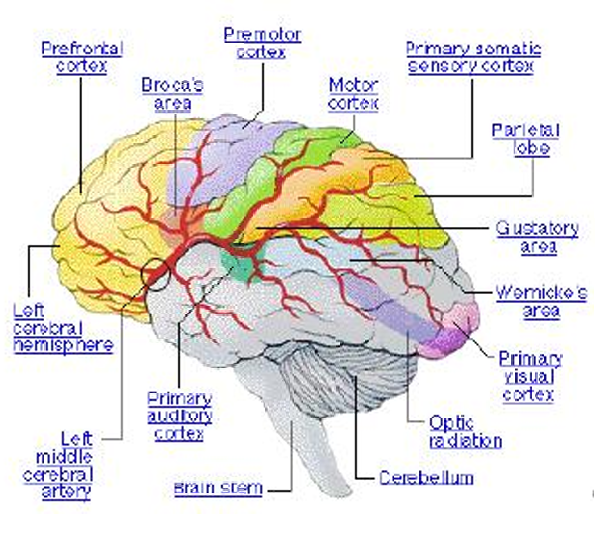
这些相似功能的神经元倾向于聚集在一起，形成特定的功能区域。

大脑在"二维"内部映射中处理来自外部世界的多维信号。这意味着大脑将多维的外部信息（如视觉、听觉、触觉等）转化为可以在大脑中以二维形式表示的内部映射。这种映射有助于大脑理解和处理复杂的外部世界。

2. 特征映射（Feature Maps）

特征映射是大脑中的一种组织方式，它将外部世界的多维信息转化为可以在大脑中以线性或平面拓扑结构（即一维或二维）表示的内部映射。

以下是一些特征映射的例子：

音调映射（Tonotopic map）：这是指大脑皮层中对声音频率的有序映射。在这个映射中，不同频率的声音被映射到皮层的不同区域，从低频到高频有序排列。
视网膜映射（Retinotopic map）：这是指视觉皮层中对视觉场的映射。在这个映射中，视觉场的中心区域（即我们视觉最敏锐的部分）在视觉皮层中被映射为具有更高分辨率的区域。
体感映射（Somatosensory map）：这是指大脑中对触觉的映射。在这个映射中，身体不同部位的触觉信息被映射到大脑皮层的特定区域，这些区域对应于身体的不同部位。

感官体验是多维的。例如，声音可以通过音高、强度、噪声等不同的维度来描述。

我们的大脑将外部多维世界的表示映射到类似的一维或二维内部表示，从而将复杂的外部信息简化为可以在大脑中更易于处理的形式。

大脑以保持拓扑结构的方式处理外部信号，也就是说大脑在处理信息时保留了信息的相对位置和结构，即使信息被映射到一个更低维度的空间。

如果我们希望模仿大脑的学习方式，我们的系统也应该能够做同样的事情。

2.1 拓扑图（Topographic Maps）

我们现在介绍拓扑图，它通过保持输入数据的邻域关系来创建一个有序的输出空间，这对于模拟大脑如何处理和组织信息具有重要意义，并且是SOM算法设计的基础。

拓扑图将竞争学习的概念扩展到包含输入和神经元周围的邻域。在SOM中，竞争学习是一种学习机制，其中神经元竞争成为输入模式的最佳匹配。拓扑图进一步扩展了这一概念，考虑了输入空间中邻近点之间的关系，以及这些点如何在输出特征空间中被映射。

我们希望输入模式空间到输出特征空间的非线性转换能够保持输入之间的邻域关系。也就是将输入数据映射到输出空间时保留输入数据的拓扑结构。

一个特征映射，其中邻近的神经元对相似的输入做出反应。

在SOM中，特征映射是指输出空间中的神经元根据输入数据的特征进行组织。邻近的神经元倾向于对相似的输入模式做出反应，这有助于创建一个有序的输出空间。

神经元选择性地调整以适应特定的输入模式，使得神经元彼此之间有序排列，为不同的输入特征创建一个有意义的坐标系统。

在SOM的学习过程中，神经元会根据输入数据的特征进行调整，以便更好地匹配输入模式。这种调整导致神经元在输出空间中有序排列，形成一个有意义的坐标系统。使得相似的输入特征在输出空间中彼此靠近，从而便于分析和理解输入数据的结构。

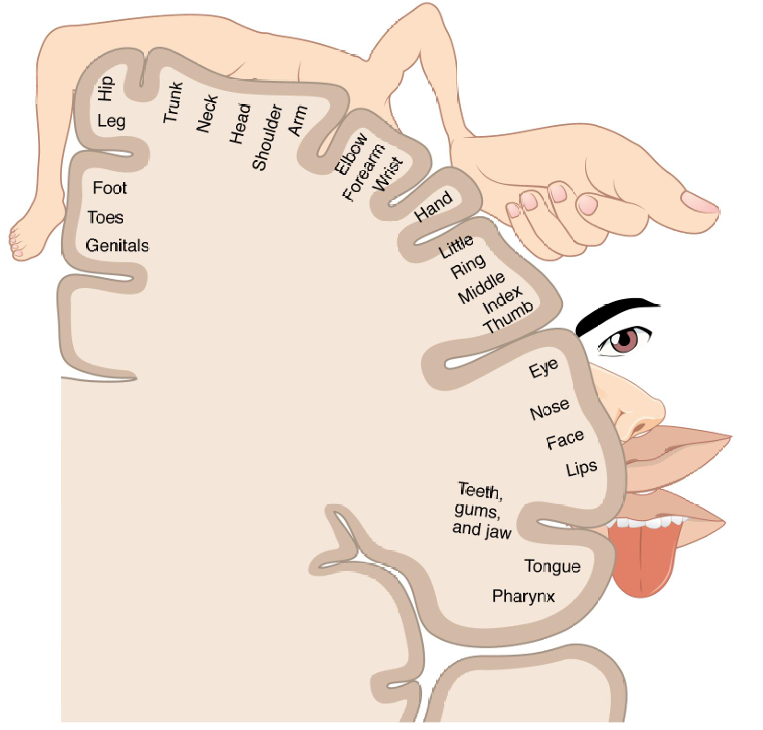
下图给出了一个具体的例子：大脑皮层的体感映射（cortical homunculus），它展示了身体各部分在大脑皮层上的对应位置。

下图展示了拓扑图（Topographic Maps）如何表示输入模式的内在统计特征。

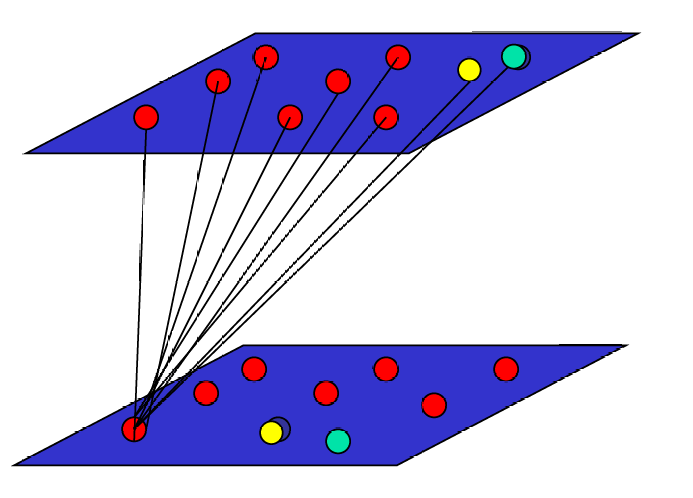
输入数据在空间上的分布位置反映了这些数据的内在统计特性。换句话说，输入数据在输入空间中彼此接近的程度，会在输出空间中以相似的方式表现出来。

如上图所示黄色球和绿色球相对较近，在输出空间中，两球的相对位置依然保持很近。

2.1.1 拓扑图的生成机制

首先它是基于活动的自组织（Activity-based self-organization）（C. von der Malsburg提出）。这是一种自组织机制，其中神经元的活动模式决定了它们的连接和组织方式。在这种机制下，神经元通过它们的活动来调整彼此之间的连接强度，从而形成有序的网络结构。

在这种机制下，神经元存在竞争和合作机制。

竞争机制：在这种机制中，神经元之间存在竞争，每个神经元都试图成为对特定输入模式的最佳响应者。这种竞争有助于选择和强化对特定输入模式最敏感的神经元。
合作机制：与竞争相对，合作机制强调神经元之间的协同作用。邻近的神经元倾向于对相似的输入模式做出反应，从而形成协同响应的神经元群。

因此人们用无监督学习网络来生成特征图，这些特征图能够表示输入数据的内在结构和关系。

通过无监督学习，网络能够自动地将输入数据映射到输出空间中，形成有序的、有意义的特征图，这些图反映了输入数据的统计特性和结构。

那现在我们如何使用高度互联的电路将基于活动的学习实现出来，从而将视觉刺激空间有序地映射到皮层表面呢？

我们现在将每一层皮层单元（cortical units）通过希伯（Hebbian）单元完全连接到视觉空间（visual space），这便是两层网络。（希伯学习是一种基于时间接近性的学习规则，即"一起激活的神经元连接在一起"。这意味着如果两个神经元经常同时激活，它们之间的连接会加强）

这些连接被描述为具有"墨西哥帽"（Mexican-hat）功能，包括短距离的兴奋（short-range excitation）和长距离的抑制（long-range inhibition）。（"墨西哥帽"函数是一种常见的空间滤波器，它在中心区域产生兴奋效应，而在周围区域产生抑制效应。这种结构有助于形成有序的映射，使得相邻的皮层单元对相似的视觉输入做出反应。）

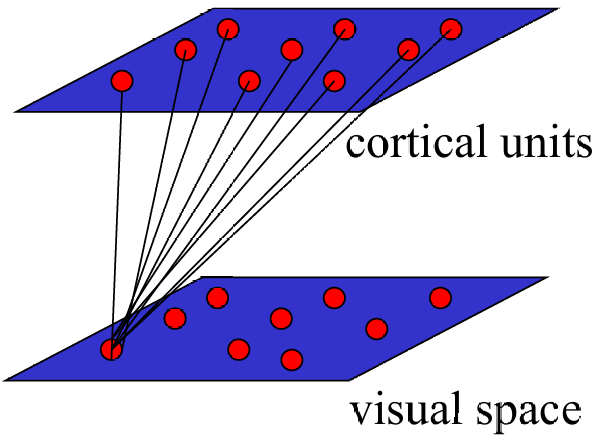
通过基于活动的自组织，在这个模型中，学习后会出现一个拓扑图，其中输入维度与输出维度相同。

我们现在要学习SOM算法（Kohonen提出），这个算法不仅可以保持输入和输出维度相同，还可以执行降维（dimensionality reduction），即输入维度可以大于输出维度。

因此我们可以将SOM是作为一种向量量化算法（向量量化是一种数据压缩技术，它将输入数据映射到一组离散的代码本向量上）。

2.1.2 自组织映射（Self-Organizing Map，SOM）

自组织映射有时也被称为Kohonen网络（Kohonen networks），这是以发明者Teuvo Kohonen的名字命名的。

SOM代表了前面讨论过的思想的具体实现。这些思想包括基于活动的自组织、竞争和合作机制、以及通过无监督学习生成特征图等。

SOM的目标是将任意维度的输入数据转换为一维或二维的离散映射。

因此下图展示了两种SOM的网络架构：

一维架构：在这种架构中，输出层是一维的，通常表示为一个线性排列的神经元。每个神经元与输入层的所有神经元相连。

二维架构：在这种架构中，输出层是二维的，通常表示为一个网格或矩阵的神经元。每个神经元也与输入层的所有神经元相连。

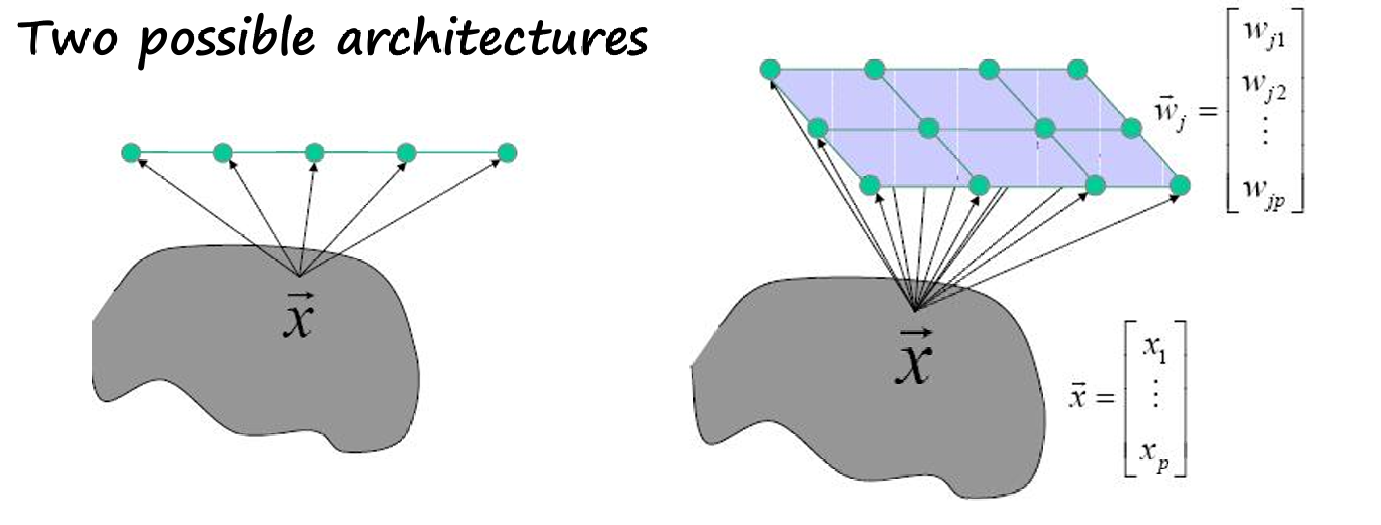
所以和前面类似，SOM是由两层神经元组成：

输入层：这一层接收原始的高维输入数据。

输出层（也称为映射层或代码本层）：这一层的神经元数量通常远少于输入层，它们代表了输入数据在低维空间中的映射。

输入层的每个神经元都与输出层的每个神经元相连。这种全连接结构允许输入数据的每个维度都影响输出层中每个神经元的状态。

输出层的每个神经元都有一个权重向量，其维度与输入向量相同。这些权重向量决定了每个神经元对输入数据的响应。

输出层的神经元被组织在一个一维或二维的格点阵列（lattice）中。在最常见的情况下，这个格点阵列是二维的，如一个矩形或六边形网格。

神经元在格点阵列中的位置定义了它们之间的距离。在SOM的学习过程中，相似的输入数据会被映射到格点阵列中相邻的位置，从而在输出空间中形成簇。

2.1.2.1 SOM算法的过程

SOM算法在权重初始化后主要包含三个过程：竞争（Competition）、合作（Cooperation）和突触适应（Synaptic Adaptation）。

竞争（Competition）：
在这一过程中，给定一个输入模式，输出层的神经元会相互竞争以确定哪个是"获胜者"（winner）。
竞争的依据是判别函数，通常是输入向量和权重向量之间的相似度。相似度越高，神经元成为获胜者的可能性就越大。
这个过程确保了对于每个输入模式，都有一个神经元（或一小群神经元）比其他神经元更匹配。
合作（Cooperation）：
获胜神经元确定了输出层中一个拓扑邻域的空间位置，这个邻域内的神经元会被激活或"兴奋"。
这意味着不仅获胜神经元会调整其权重，其邻域内的神经元也会参与调整，尽管调整的程度可能较小。
这种合作机制有助于保持输入空间的拓扑结构在输出空间中的映射，使得相似的输入模式在输出空间中也靠近。
突触适应（Synaptic Adaptation）：
在这一过程中，被激活的神经元（包括获胜神经元及其邻域内的神经元）会调整它们的权重，使得判别函数的值增加。
换句话说，权重的调整使得相似的输入在未来能够引起获胜神经元更强的反应。
权重的调整通常遵循Hebbian学习规则，即"一起激活的神经元连接在一起"，并且调整的程度会随着距离获胜神经元的距离增加而减小。

因此用一句话概括SOM算法的学习原则那就是：竞争学习，其中获胜者的影响会"溢出"到邻居。

这种"溢出"效应有助于网络在处理相似输入时表现出更好的泛化能力，同时也有助于网络的自组织和特征发现。

2.1.2.1.1 初始化（Initialization）

刚刚提到了SOM算法的主要过程，现在从头开始介绍。

在SOM中，输出层通常被组织成一个网格结构，这个网格的大小和结构在训练开始前就固定好了（a priori），即在训练之前就已经确定。

这个网格可以是一维的（如一条直线）或二维的（如一个矩形或六边形网格），但大多数情况下使用的是二维网格。

网格中的每个节点代表一个神经元，每个神经元都有一个权重向量 w ⃗ j \vec{w}_j w j，其维度与输入向量相同。

权重向量决定了每个神经元对输入数据的响应。在初始化阶段，这些权重向量通常被随机设置，或者设置为输入数据的均值。

下图展示了一个二维网络，其中每个绿色点代表一个神经元。

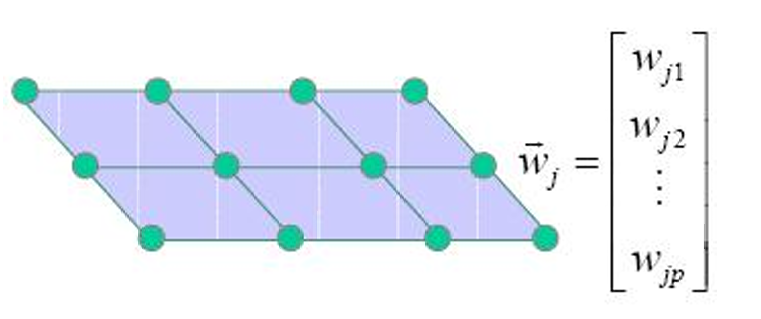
每个神经元的权重向量 w ⃗ j \vec{w}j w j表示为一个列向量，其中包含了与输入向量维度相同的元素 w j 1 , w j 2 , ... , w j p w{j1}, w_{j2}, \ldots, w_{jp} wj1,wj2,...,wjp。

2.1.2.1.2 竞争过程

给定一个输入向量 x ⃗ j \vec{x}_j x j ，算法会计算它与输出层中所有神经元的权重向量 w ⃗ j \vec{w}_j w j之间的相似度。

相似度可以通过不同的方式计算：

内积： w j T x ⃗ {w}_j^T \vec{x} wjTx ，表示权重向量和输入向量的点积。
距离： ∥ x ⃗ − w ⃗ j ∥ \| \vec{x} - \vec{w}_j \| ∥x −w j∥，表示输入向量和权重向量之间的欧氏距离。

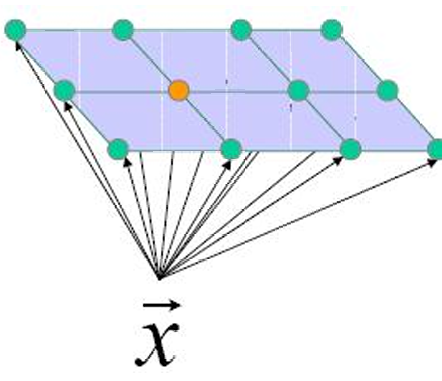
因此根据计算的相似度，算法会选择一个"获胜神经元" j ∗ j^* j∗。

获胜神经元的选择可以通过两种方式：

最大化内积： j ∗ = argmax j ( w ⃗ j T x ⃗ ) j^* = \text{argmax}_j \left( \vec{w}_j^T \vec{x} \right) j∗=argmaxj(w jTx )，即选择与输入向量内积最大的权重向量对应的神经元。
最小化距离： j ∗ = argmin j ( ∥ x ⃗ − w ⃗ j ∥ ) j^* = \text{argmin}_j \left( \| \vec{x} - \vec{w}_j \| \right) j∗=argminj(∥x −w j∥)，即选择与输入向量距离最小的权重向量对应的神经元。

2.1.2.1.3 合作过程

获胜神经元定位合作神经元的拓扑邻域中心。

神经元的激发倾向于影响其直接邻域内的神经元。当一个神经元被激发（即成为获胜神经元）时，它不仅自身会调整权重，还会影响其在输出层网格中的邻域内的神经元。这种影响通常是根据神经元之间的距离来确定的，距离获胜神经元越近的神经元受到的影响越大。

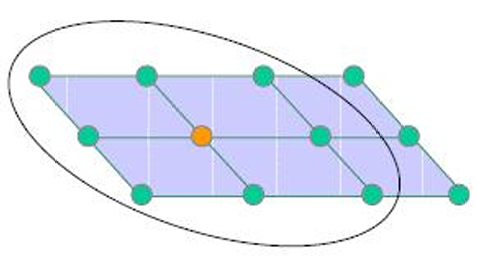
邻域由函数 h j , i h_{j,i} hj,i描述了神经元 j j j和 i i i之间的邻域关系。数学表达式为：
h j , i = exp ⁡ ( − d j , i 2 2 σ 2 ) h_{j,i} = \exp\left(-\frac{d_{j,i}^2}{2\sigma^2}\right) hj,i=exp(−2σ2dj,i2)
d j , i d_{j,i} dj,i是神经元 j j j和 i i i之间的距离。
σ σ σ是一个参数，控制邻域的宽度。随着学习过程的进行， σ σ σ通常会逐渐减小，使得邻域范围变小，从而提高网络的分辨能力。

拓扑邻域 h j , i h_{j,i} hj,i对称分布在获胜神经元（即对输入模式响应最好的神经元）周围，并在获胜神经元处达到最大值。邻域的幅度随着与获胜神经元的横向距离增加而单调递减。

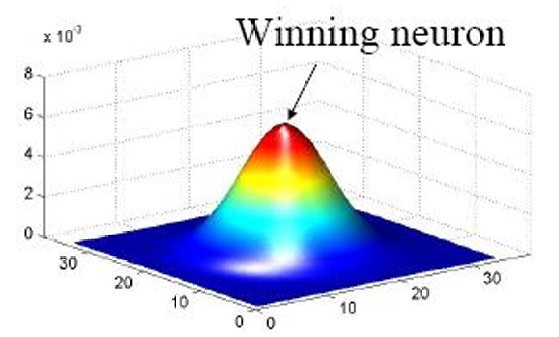
在SOM的训练过程中，拓扑邻域 h j , i h_{j,i} hj,i会随着时间的推移而逐渐缩小。这意味着随着训练的进行，只有越来越接近获胜神经元的神经元才会受到显著的影响并参与权重的更新。

邻域收缩的动态由参数 σ ( t ) σ(t) σ(t)控制，其表达式为：
σ ( t ) = σ 0 exp ⁡ ( − t τ 1 ) \sigma(t) = \sigma_0 \exp\left(-\frac{t}{\tau_1}\right) σ(t)=σ0exp(−τ1t)

其中， σ 0 \sigma_0 σ0是初始邻域宽度， t t t是当前训练步数， τ 1 \tau_1 τ1是控制邻域收缩速度的参数。

拓扑邻域函数 h j , i ( t ) h_{j,i}(t) hj,i(t) 随时间变化的表达式为：
h j , i ( t ) = exp ⁡ ( − d j , i 2 2 σ 2 ( t ) ) h_{j,i}(t) = \exp\left(-\frac{d_{j,i}^2}{2\sigma^2(t)}\right) hj,i(t)=exp(−2σ2(t)dj,i2)

其中， d j , i d_{j,i} dj,i是神经元 j j j和 i i i之间的距离。

即使某些神经元不是非常接近获胜神经元，它们仍然可以更新。这是通过让拓扑邻域随时间逐渐缩小实现的，从而使得在训练初期较远的神经元也能参与更新，而在训练后期只有非常接近获胜神经元的神经元才会更新。

2.1.2.1.3.1 邻域（neighborhood）

在SOM训练的初期，使用较大的邻域可以促进全局排序（Good global ordering），即帮助整个网络形成对输入空间的全局理解。

然而，大邻域可能导致局部拟合不佳（Bad local fit），因为此时对输入细节的捕捉不够精细。

当训练进行到后期，减小邻域可以提高局部拟合（Good local fit），即更好地捕捉输入数据的细节和局部特征。

但是，小邻域可能不利于全局排序（Bad global ordering），因为此时网络可能过于关注局部特征，而忽略了全局结构。

所以为了平衡全局排序和局部拟合，我们通过逐渐缩小邻域，SOM可以在训练的不同阶段平衡全局排序和局部拟合，从而获得两者的优点。

这种方法允许网络在初期快速学习输入数据的全局结构，而在后期逐渐细化这些结构，以更好地适应输入数据的细节。

排序阶段（Ordering phase），使用较大的邻域来促进全局排序，帮助网络形成对输入空间的整体理解。

收敛阶段（Convergence phase），使用逐渐减小邻域以提高局部拟合，使网络能够更精细地调整权重，以更好地适应输入数据的细节。

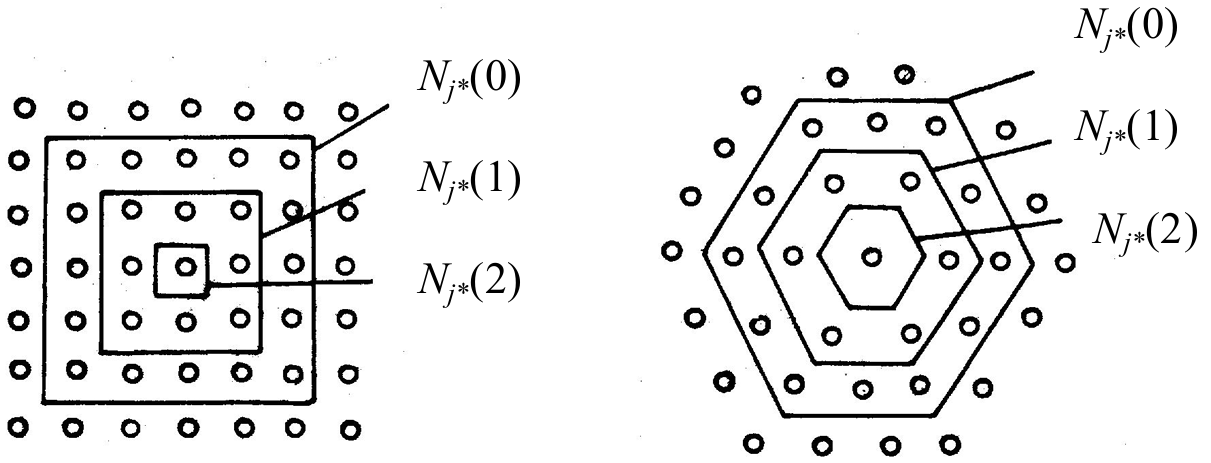
上图左侧展示了一个矩形邻域的例子，其中每个神经元的邻域包括其周围的神经元。邻域的层次从内到外标记为 N j ∗ ( 0 ) N_{j^*}(0) Nj∗(0)， N j ∗ ( 1 ) N_{j^*}(1) Nj∗(1)， N j ∗ ( 2 ) N_{j^*}(2) Nj∗(2)，表示不同的邻域范围。

右侧展示的是六边形邻域的例子。

使用平面阵列的神经元，无论是矩形还是六边形邻域，输入向量 x ⃗ \vec{x} x 都会同时应用于所有节点。这意味着每个神经元都会根据输入向量和自己的权重向量计算相似度，并参与竞争过程。

2.1.2.1.4 适应过程

自适应过程，也就是权重更新的步骤。

权重更新的公式为： w ⃗ j ( t + 1 ) = w ⃗ j ( t ) + η ( t ) h j , i ( t ) ( x ⃗ − w ⃗ j ( t ) ) \vec{w}_j(t+1) = \vec{w}j(t) + \eta(t) h{j,i}(t) (\vec{x} - \vec{w}_j(t)) w j(t+1)=w j(t)+η(t)hj,i(t)(x −w j(t))

其中， w ⃗ j ( t ) \vec{w}j(t) w j(t)是在时间 t t t时神经元 j j j的权重向量， x ⃗ \vec{x} x 是输入向量， η ( t ) \eta(t) η(t)是学习率， h j , i ( t ) h{j,i}(t) hj,i(t)是拓扑邻域函数。

学习率 η ( t ) \eta(t) η(t)控制权重更新的步长，其表达式为：
η ( t ) = η 0 exp ⁡ ( − t τ 1 ) \eta(t) = \eta_0 \exp\left(-\frac{t}{\tau_1}\right) η(t)=η0exp(−τ1t)

这里， η 0 \eta_0 η0是初始学习率， t t t是当前训练步数， τ 1 \tau_1 τ1是控制学习率下降速度的参数。

邻域函数 h j , i ( t ) h_{j,i}(t) hj,i(t)定义了神经元 j j j和 i i i在时间 t t t时的邻域关系，其表达式为：
h j , i ( t ) = exp ⁡ ( − d j , i 2 2 σ 2 ( t ) ) h_{j,i}(t) = \exp\left(-\frac{d_{j,i}^2}{2\sigma^2(t)}\right) hj,i(t)=exp(−2σ2(t)dj,i2)

其中， d j , i d_{j,i} dj,i是神经元 j j j和 i i i之间的距离， σ ( t ) \sigma(t) σ(t)是随时间变化的邻域宽度参数。

2.1.2.1.4.1 学习率（Learning Rate）

对于控制权重更新步长的学习率，我们有多个选项：

线性递减：
η ( t ) = − a t + b η(t)=−at+b η(t)=−at+b
这种学习率随时间线性递减，从初始值 b b b开始，以斜率 − a −a −a减少。
指数递减：
η ( t ) = e x p ( − a t ) + b η(t)=exp(−at)+b η(t)=exp(−at)+b
这种学习率以指数方式递减，从 b b b开始，递减速率由参数 a a a控制。
时间倒数递减：
η ( t ) = 1 a t + b \eta(t) = \frac{1}{at} + b η(t)=at1+b
这种学习率随时间的倒数递减，从 b b b开始，递减速率由参数 a a a控制。

下图展示了这三种学习率随时间变化的曲线。

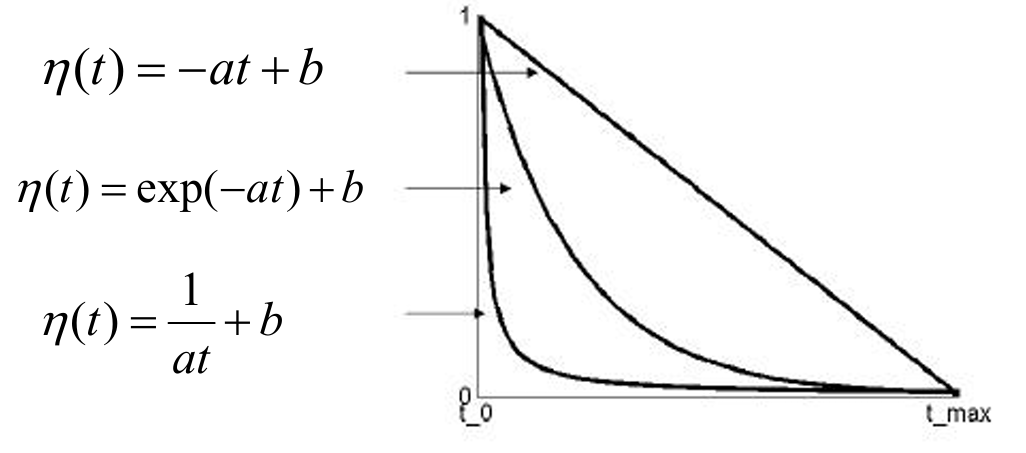
2.1.2.2 SOM算法的训练流程

初始化（Initialization）：

在训练开始之前，需要对网络进行初始化。这通常涉及随机设置输出层神经元的权重向量，或者将它们初始化为输入数据的均值。
抽取输入样本（Draw an input sample x ⃗ \vec{x} x ）：

从输入数据集中随机抽取一个输入样本 x ⃗ \vec{x} x 。
获胜神经元（Winner neuron j ∗ j^* j∗）：

计算输入样本与所有神经元权重向量之间的相似度，可以通过内积或距离计算。

选择相似度最高的神经元作为获胜神经元 j ∗ j^* j∗。这可以通过最大化内积 argmax j ( w ⃗ j T x ⃗ ) \text{argmax}_j (\vec{w}_j^T \vec{x}) argmaxj(w jTx )或最小化距离 argmin j ( ∥ x ⃗ − w ⃗ j ∥ ) \text{argmin}_j (\|\vec{x} - \vec{w}_j\|) argminj(∥x −w j∥)来实现。
更新（Update）：

根据获胜神经元及其邻域内神经元的激活程度更新权重。

权重更新公式为：
w ⃗ j ( t + 1 ) = w ⃗ j ( t ) + η ( t ) h j , i ( t ) ( x ⃗ − w ⃗ j ( t ) ) \vec{w}_j(t+1) = \vec{w}j(t) + \eta(t) h{j,i}(t) (\vec{x} - \vec{w}_j(t)) w j(t+1)=w j(t)+η(t)hj,i(t)(x −w j(t))

其中， η ( t ) \eta(t) η(t)是学习率， h j , i ( t ) h_{j,i}(t) hj,i(t)是邻域函数，定义了神经元 j j j和 i i i在时间 t t t时的邻域关系：
h j , i ( t ) = exp ⁡ ( − d j , i 2 2 σ 2 ( t ) ) h_{j,i}(t) = \exp\left(-\frac{d_{j,i}^2}{2\sigma^2(t)}\right) hj,i(t)=exp(−2σ2(t)dj,i2)

学习率 η ( t ) \eta(t) η(t)随时间递减：
η ( t ) = η 0 exp ⁡ ( − t τ 1 ) \eta(t) = \eta_0 \exp\left(-\frac{t}{\tau_1}\right) η(t)=η0exp(−τ1t)
迭代：

重复上述步骤2至步骤4，直到达到预定的训练轮数或满足其他停止条件。

2.1.2.3 SOM算法的特性

我们现在总结一下SOM算法的几个特征：

近似输入空间（Approximate the input space）：
SOM能够将高维输入数据映射到低维空间（通常是一维或二维），同时尽可能保留输入数据的全局结构和特征。这种映射提供了输入数据的简化表示，有助于数据的可视化和理解。
拓扑排序（Topological ordering）：
SOM保持了输入数据的拓扑结构，即输入空间中相近的数据点在输出空间中也保持相近。这种拓扑保持特性使得SOM能够揭示输入数据的内在结构和关系。
密度匹配（Density matching）：
SOM能够根据输入数据的分布密度调整输出空间中神经元的分布。在输入数据密集的区域，输出空间中会有更多神经元来表示这些区域；而在数据稀疏的区域，神经元的分布会相对稀疏。这种特性有助于捕捉输入数据的分布特征。
特征选择（Feature selection）：
SOM能够从输入数据中自动提取和选择重要的特征。这些特征反映了输入数据的底层分布特性，有助于识别数据中的关键模式和趋势。

3. 学习向量量化器（Learning Vector Quantizer，LVQ）

3.1 简单竞争学习（Simple Competitive Learning）

我们先回顾一下之前章节学习的知识。

简单竞争学习是一种无监督学习方法，用于模式识别和聚类。具体步骤如下：

初始化原型向量（Prototype Vectors）：
首先，需要初始化 K K K个原型向量，这些向量代表 K K K个不同的类别或簇。
呈现单个样本（Present a Single Example）：
然后，逐个呈现数据集中的样本。
识别最近的原型（Identify the Closest Prototype）：
对于每个样本，算法需要识别与其最接近的原型，即找到所谓的"胜者"（winner）。
移动胜者（Move the Winner）：
接着，将胜者原型向量向样本移动，使其更接近该样本。

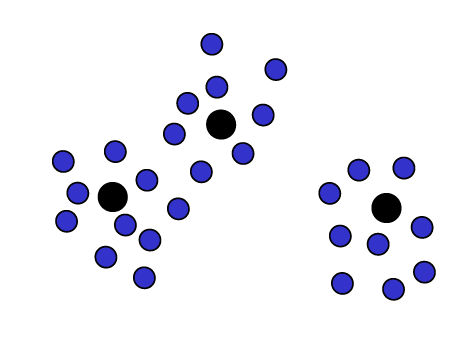
这个过程直观且合理，因为它将原型放置在数据密度较高的区域，从而更好地表示数据中的模式。
它还能识别出特征的最重要组合，有助于发现数据中的结构和模式。

3.2 向量量化（Vector Quantization）

向量量化的目标是将一组给定的输入向量分类到 M M M个类别中。

这是通过使用竞争学习算法实现的，其中每个类别由一个原型向量（prototype vector）表示。

任何向量都可以通过它所属的类别来表示，即它落入的类别。

在数据压缩中，竞争性学习的一个重要应用是将整个模式空间划分为多个独立的子空间。

一组 M M M个单元代表一组原型向量，这些原型向量构成了一个"码本"（CODEBOOK）。

新的模式 x x x根据其与原型向量之间的欧几里得距离来分配到一个类别中。

码本是一组中心点（centroids）、码字（codewords）或码向量（codevectors）的集合，表示为 { m 1 , m 2 , ... , m K } \{ m_1, m_2, \ldots, m_K \} {m1,m2,...,mK}。这些中心点或原型向量用于表示数据集中的各个类别。

量化函数 q ( x i ) = m k q(x_i) = m_k q(xi)=mk用于将输入向量 x i x_i xi映射到最近的中心点 m k m_k mk。这个过程通常使用最近邻函数来实现，即找到与输入向量最接近的中心点。

Voronoi图（Voronoi diagram）是一种将平面划分为多个区域的方法，这些区域基于特定子集中点之间的距离。

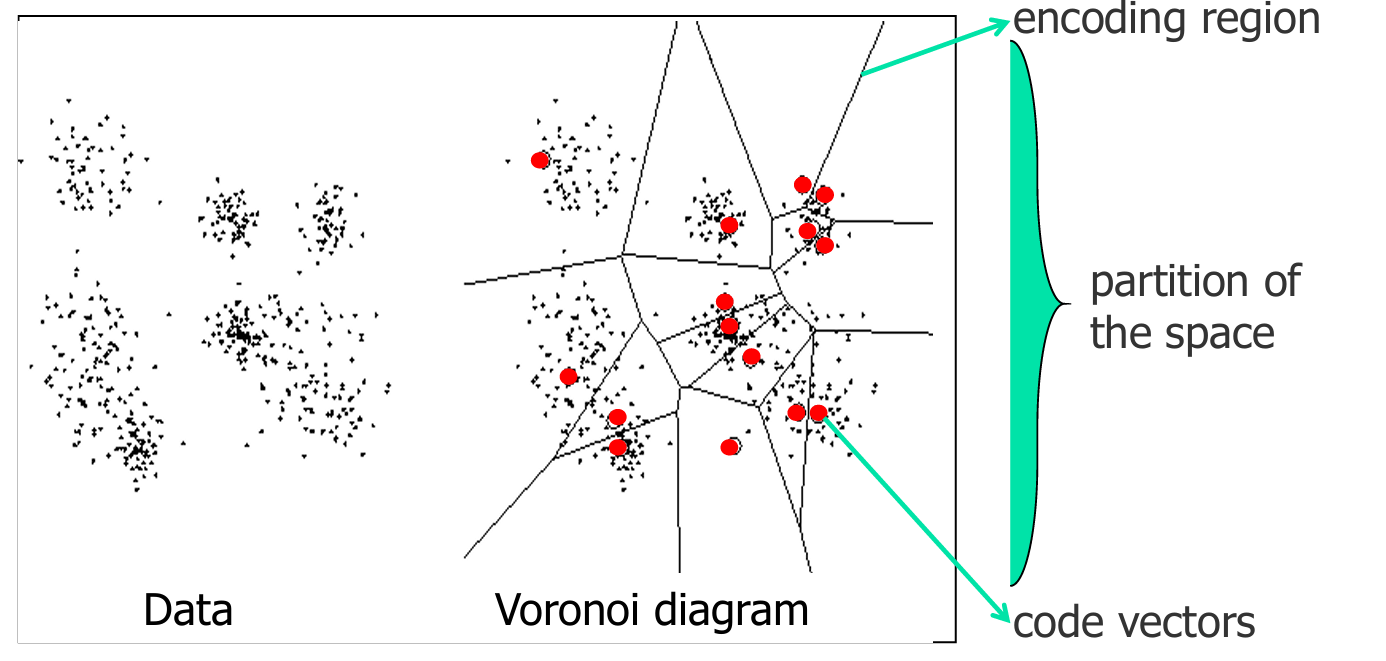
左侧（Data）：显示了一组数据点，这些点可能是输入向量，它们在空间中随机分布。

右侧（Voronoi diagram）：显示了这些数据点如何被划分为不同的Voronoi单元。每个单元由一个中心点（红色点）定义，这些中心点是码向量（code vectors）。每个单元包含所有比任何其他中心点更接近该中心点的数据点。

编码区域（encoding region）：指的是Voronoi单元，即数据点被分配到的区域。

空间划分（partition of the space）：指的是整个平面被Voronoi单元划分的情况。

码向量（code vectors）：指的是定义Voronoi单元中心的点，这些点是量化过程中的原型向量。

在VQ技术中，会形成一组局部Voronoi中心来表示输入向量。这些中心是参考向量，用于将输入向量映射到最近的中心。

对于一组 M M M个参考向量 { w ⃗ 1 , w ⃗ 2 , ... , w ⃗ M } \{ \vec{w}_1, \vec{w}_2, \ldots, \vec{w}_M \} {w 1,w 2,...,w M}，一个输入向量 x ⃗ \vec{x} x 被认为是被 w ⃗ k \vec{w}_k w k最佳匹配的，如果定义的失真度量（如平方欧氏距离 ∥ x ⃗ − w ⃗ k ∥ 2 \| \vec{x} - \vec{w}_k \|^2 ∥x −w k∥2）是最小的。

参考向量将输入空间 R L R^L RL分割成Voronoi单元或多边形。每个单元定义为：
V k = { x ⃗ ∈ R L ∣ ∥ x ⃗ − w ⃗ k ∥ ≤ ∥ x ⃗ − w ⃗ l ∥ , ∀ l } V_k = \{ \vec{x} \in R^L \mid \| \vec{x} - \vec{w}_k \| \leq \| \vec{x} - \vec{w}_l \|, \forall l \} Vk={x ∈RL∣∥x −w k∥≤∥x −w l∥,∀l}

这意味着对于每个 V k V_k Vk ，所有输入向量 x ⃗ \vec{x} x 到 w k ⃗ \vec{w_k} wk 的距离都小于或等于到其他任何参考向量 w l ⃗ \vec{w_l} wl 的距离。

可能的参考向量的集合被称为量化器的码本（codebook），其成员被称为码向量（code vectors）。

这些码向量是输入空间的离散表示，每个码向量代表输入空间的一个区域。

SOM算法提供了一种无监督的方法来计算Voronoi向量，即码向量。

通过SOM算法，可以自动地发现输入数据的内在结构，并据此生成码向量，这些码向量能够很好地代表输入数据的分布。

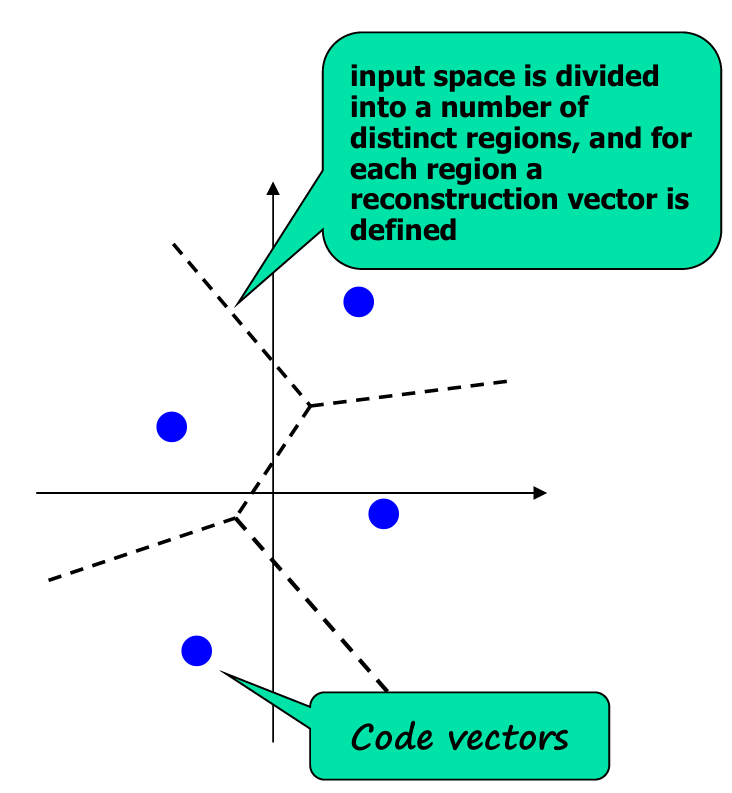
上图展示了输入空间如何被划分为不同的区域，每个区域都有一个重建向量（reconstruction vector）定义。

这些重建向量对应于码向量，它们是输入空间中各区域的代表点。

3.3 学习向量量化器（Learning Vector Quantizer，LVQ）

LVQ是一种结合了自组织映射（Self-Organizing Map，简称SOM）和监督学习技术的分类方法。

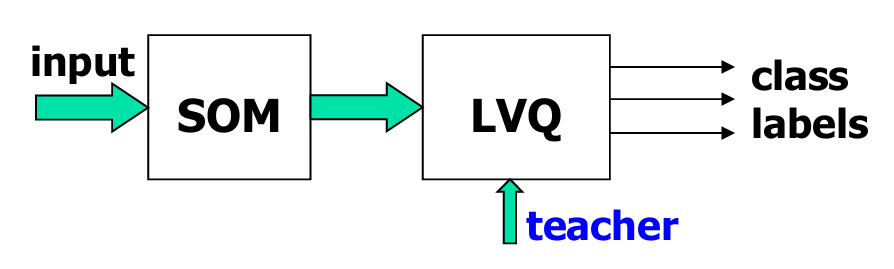
如上图所示，输入数据首先通过SOM进行处理，SOM是一个无监督学习算法，用于将输入数据映射到一个低维空间，并形成Voronoi单元。

然后，这些映射后的数据被送入LVQ模块。LVQ是一个监督学习模块，它使用类别信息（class labels）来调整Voronoi向量（即码向量）的位置。

在LVQ中，教师信号指的是输入数据的类别标签。这些标签用于指导LVQ的学习过程，使得Voronoi向量能够更好地代表不同类别的数据。

LVQ是一种监督学习技术，它利用类别信息来微调Voronoi向量。这个过程使得Voronoi向量不仅能够捕捉输入数据的分布特征，还能够反映数据的类别信息。

通过这种方式，LVQ能够改善分类器的决策区域，使得分类器在处理新的输入数据时能够做出更准确的分类决策。

3.3.1 LVQ1

LVQ算法有两个变体，我们先介绍最早的LVQ1.

算法步骤如下：

随机选择输入向量：
从输入空间中随机选择一个输入向量 x ⃗ \vec{x} x
比较类别标签：
比较输入向量 x ⃗ \vec{x} x 的类别标签和一个Voronoi向量 w ⃗ \vec{w} w 的类别标签（这里 w ⃗ \vec{w} w 是SOM中的获胜神经元）。
类别标签一致时的权重更新：
如果 x ⃗ \vec{x} x 和 w ⃗ \vec{w} w 的类别标签一致（即它们属于同一个类别），则将Voronoi向量 w ⃗ \vec{w} w 向输入向量 x ⃗ \vec{x} x 的方向移动，以更好地代表该类别的数据。权重更新公式为：
w ⃗ new = w ⃗ old + η ( x ⃗ − w ⃗ ) \vec{w}^{\text{new}} = \vec{w}^{\text{old}} + \eta (\vec{x} - \vec{w}) w new=w old+η(x −w )
这里， η \eta η是学习率，控制权重更新的步长。
类别标签不一致时的权重更新：
如果 x ⃗ \vec{x} x 和 w ⃗ \vec{w} w 的类别标签不一致（即它们属于不同的类别），则将Voronoi向量 w ⃗ \vec{w} w 从输入向量 x ⃗ \vec{x} x 的方向移开，以减少对错误类别的表示。权重更新公式为：
w ⃗ new = w ⃗ old − η ( x ⃗ − w ⃗ ) \vec{w}^{\text{new}} = \vec{w}^{\text{old}} - \eta (\vec{x} - \vec{w}) w new=w old−η(x −w )

3.3.2 LVQ2

LVQ2是对LVQ1的改进，它在权重更新时考虑了更多的因素，以提高分类性能。

初始化原型向量：
为不同的类别初始化一组原型向量。这些原型向量是网络中的参考向量，用于将输入向量映射到最近的类别。
呈现单个样本：
从数据集中随机抽取一个输入样本。
识别最近的原型：
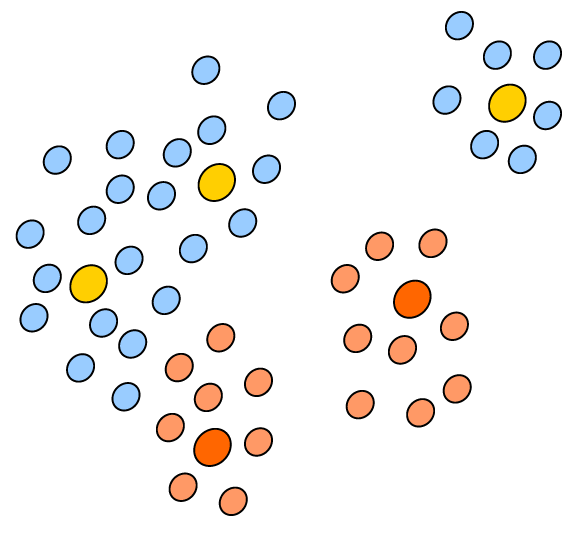
计算输入样本与所有原型向量之间的距离，找出最近的"正确"原型（即与输入样本属于同一类别的原型）和最近的"错误"原型（即与输入样本不属于同一类别的原型）。
移动相应的获胜者：
根据原型向量与输入样本的类别标签是否一致，调整原型向量的位置：
如果原型向量是"正确"的（即与输入样本属于同一类别），则将该原型向量向输入样本移动，使其更好地代表该类别的数据。
如果原型向量是"错误"的（即与输入样本不属于同一类别），则将该原型向量从输入样本的方向移开，以减少对错误类别的表示。

3.4 小结

首先LVQ的停止条件如下：

码本向量稳定：当码本向量（即原型向量或权重向量）的变化非常小或不再显著变化时，可以停止训练。
达到最大迭代次数：当达到预设的最大迭代次数（epochs）时，训练也可以停止。

优点如下：

合理、直观、灵活：LVQ算法基于直观的原型向量调整机制，易于理解和实现，且可以灵活应用于不同的问题。
快速且易于实现：算法相对简单，实现起来快速，不需要复杂的数学运算或优化技术。
广泛应用于结构化数据分类问题：LVQ算法在各种涉及结构化数据分类的问题中都有应用，如图像识别、语音识别等。

缺点如下：

对重叠类别不稳定：当类别之间有较大重叠时，LVQ算法可能无法有效地区分这些类别，因为算法倾向于将原型向量推向数据密集区域，而不考虑类别边界。
对初始化非常敏感：算法的性能很大程度上依赖于初始原型向量的设置。不当的初始化可能导致算法收敛到局部最优解，影响最终的分类效果。