当你打开地图 APP 规划出行路线时,是否想过背后的数据结构在默默 "工作"?从 A 地到 B 地的多条路径、不同道路的距离(权重)、单行道(有向)限制,这些都能通过 "带权有向图" 完美建模。而今天要揭秘的 "邻接链表",就是高效存储和操作这类复杂图结构的 "幕后功臣"。
一、先搞懂:带权有向图到底是什么?
在数据结构的世界里,"图" 不再是纸上简单的线条画,而是由 "顶点"(比如地图上的路口、景点)和 "边"(比如连接两点的道路)组成的复杂网络。而 "带权有向图",就是给这个网络加上了两个关键属性:
- 有向性:边是 "单向" 的,就像现实中的单行道。比如从路口 A 能直接到路口 B,但路口 B 不能直接回路口 A,这条边就只有 "A→B" 的方向。
- 权重:边带有 "数值信息",可以表示距离、时间、费用等。比如 A 到 B 的道路长 10 公里,那这条边的权重就是 10。
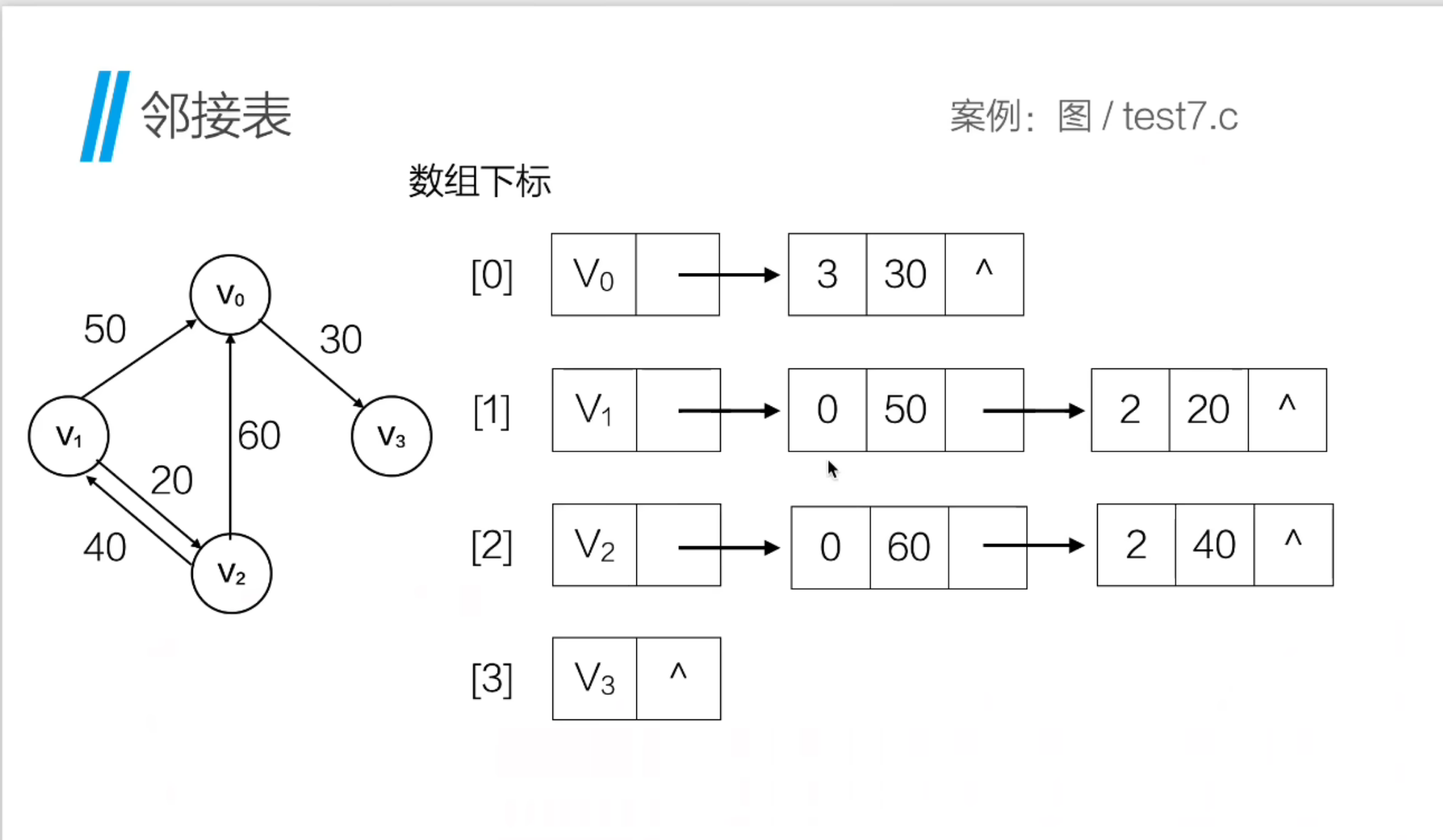
举个简单的例子:假设我们有 4 个顶点(编号 0-3,代表 4 个路口),5 条带权有向边:1→0(50)、2→0(60)、0→3(30)、1→2(20)、2→1(40)。这就是一个典型的带权有向图,而如何高效存储这些顶点和边的关系,就轮到 "邻接链表" 登场了。
二、为什么选邻接链表?比数组更灵活的存储方案
存储图的方式有很多,最直观的是 "邻接矩阵"------ 用一个二维数组记录顶点间的连接关系。但邻接矩阵有个明显的缺点:如果图的顶点多但边少(比如稀疏图,现实中大部分图都是如此),会浪费大量存储空间(比如 100 个顶点的图,需要 100×100 的数组,但实际边可能只有几十条)。
而邻接链表完美解决了这个问题:它为每个顶点单独建一个 "链表",链表中只存储该顶点直接指向的 "邻接顶点" 和对应的 "边权重"。简单来说,就是 "谁和我直接相连、连的边有什么属性,我就记下来,无关的一概不存"。
比如前面提到的顶点 1,它的邻接链表只会记录 "指向 0(权重 10)" 和 "指向 2(权重 20)" 这两个信息,既节省空间,后续遍历、修改时也更高效。
三、手把手实现:用 C 语言搭建带权有向图的邻接链表
光说不练假把式,下面我们用 C 语言一步步实现带权有向图的邻接链表,从结构体定义到图的创建、输出,每一步都清晰可见。
1. 定义核心结构体:搭好 "骨架"
首先要定义两个关键结构体:"边表节点" 和 "顶点节点",再用一个 "图结构体" 把它们整合起来。
- 边表节点(Edgenode):存储邻接顶点的下标(adx)、边的权重(weight),以及指向下一个边节点的指针(next)------ 相当于链表的 "链节"。
- 顶点节点(Vertexnode):存储顶点自身的信息(data),以及指向该顶点第一条边的指针(firstedge)------ 相当于链表的 "表头"。
- 图结构体(GrphAdjlist):包含顶点数组(adjlist)、顶点总数(vernum)和边总数(edgenum)------ 相当于整个图的 "总控面板"。
代码实现如下(已加关键注释):
#include <stdio.h>
#include <stdlib.h>
#define maxver 100 // 最大顶点数,可根据需求调整
// 边表节点:存储邻接顶点和权重
typedef struct Edgenode{
int adx; // 邻接顶点在顶点数组中的下标
int weight; // 边的权重(如距离、时间)
Edgenode *next; // 指向下一个边节点
}Edgenode;
// 顶点节点:存储顶点信息和第一条边的指针
typedef struct Vertexnode{
int data; // 顶点信息(如编号0、1、2)
Edgenode* firstedge; // 指向该顶点的第一条边
}Vertexnode, Adjlist[maxver]; // Adjlist相当于Vertexnode数组
// 图结构体:整合顶点数组、顶点数和边数
typedef struct GrphAdjlist{
Adjlist adjlist; // 邻接表(顶点数组)
int vernum; // 顶点总数
int edgenum; // 边总数
}GrphAdjlist;
2. 创建图:给 "骨架" 填内容
创建图的核心是 "初始化顶点" 和 "构建邻接链表"。这里我们用 "头插法" 添加边节点 ------ 因为头插法不需要遍历链表尾部,操作更高效(适合边数较多的场景)。
步骤拆解:
- 初始化顶点总数(vernum)和边总数(edgenum)。
- 给每个顶点赋值(比如编号 0-3),并将其第一条边的指针设为 NULL(初始时没有边)。
- 定义带权有向边的数组(比如前面提到的 5 条边),遍历每条边,为其创建边节点,并用头插法插入到对应顶点的邻接链表中。
代码实现:
// 创建带权有向图(邻接链表版)
void create_grph(GrphAdjlist* G){
// 1. 初始化顶点数和边数(可根据实际需求修改)
G->edgenum = 5; // 5条边
G->vernum = 4; // 4个顶点(编号0-3)
// 2. 初始化顶点:赋值+第一条边为空
for(int i=0; i<G->vernum; i++){
G->adjlist[i].data = i; // 顶点编号0、1、2、3
G->adjlist[i].firstedge = NULL; // 初始无关联边
}
// 3. 定义带权有向边:{起点, 终点, 权重}
int edges[5][3] = {
{1,0,10}, // 1→0,权重50
{2,0,30}, // 2→0,权重60
{0,3,20}, // 0→3,权重30
{1,2,20}, // 1→2,权重20
{2,1,40} // 2→1,权重40
};
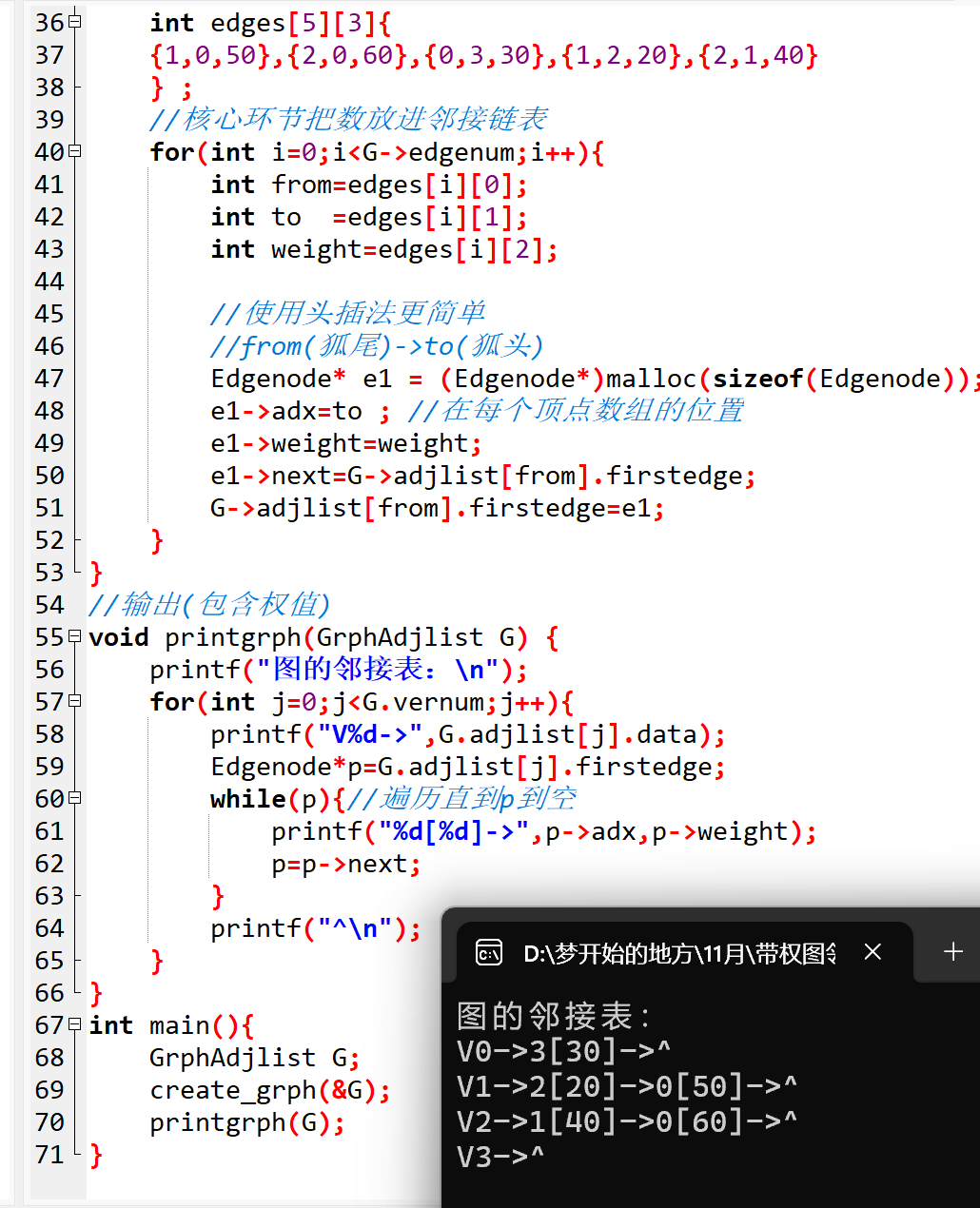
// 4. 用头插法构建邻接链表
for(int i=0; i<G->edgenum; i++){
int from = edges[i][0]; // 边的起点
int to = edges[i][1]; // 边的终点
int weight = edges[i][2];// 边的权重
// 创建新的边节点
Edgenode* e1 = (Edgenode*)malloc(sizeof(Edgenode));
e1->adx = to; // 记录终点下标
e1->weight = weight; // 记录权重
// 头插法:新节点指向当前第一条边,再让顶点指向新节点
e1->next = G->adjlist[from].firstedge;
G->adjlist[from].firstedge = e1;
}
}
3. 输出图:直观查看邻接链表
为了验证图是否创建成功,我们写一个打印函数,遍历每个顶点的邻接链表,输出 "顶点→邻接顶点 [权重]→...→^" 的格式(^ 表示链表结束)。
代码实现:
// 输出带权有向图的邻接表
void printgrph(GrphAdjlist G) {
printf("带权有向图的邻接表:\n");
for(int j=0; j<G.vernum; j++){
// 先打印当前顶点
printf("V%d->", G.adjlist[j].data);
// 遍历该顶点的邻接链表
Edgenode* p = G.adjlist[j].firstedge;
while(p != NULL){ // 直到链表末尾
printf("%d[%d]->", p->adx, p->weight); // 输出邻接顶点和权重
p = p->next; // 指向下一个边节点
}
printf("^\n"); // 标记链表结束
}
}
4. 主函数:一键运行看效果
最后写主函数,创建图、打印图,就能直观看到邻接链表的结构了。
int main(){
GrphAdjlist G; // 定义一个图
create_grph(&G); // 创建图(传地址,修改原图)
printgrph(G); // 打印图
return 0;
}
运行结果如下(和我们定义的边完全匹配):
带权有向图的邻接表:
V0->3[30]->^
V1->2[20]->0[50]->^
V2->1[40]->0[60]->^
V3->^
四、邻接链表的 "隐藏优势":不止省空间
可能有人会问:邻接链表除了省空间,还有什么用?其实它在图的核心操作中优势明显:
- 遍历高效:比如要找顶点 1 的所有出边,直接遍历它的邻接链表即可,不用像邻接矩阵那样遍历整行(100 个顶点就要查 100 次,哪怕只有 2 条边)。
- 修改灵活:新增或删除一条边时,只需在对应顶点的邻接链表中操作(头插法 / 删除节点),时间复杂度是 O (1)(邻接矩阵是 O (1),但空间浪费多)。
- 适配带权图:边节点中可以轻松添加 "权重" 字段,还能扩展其他属性(比如道路的限速、拥堵情况),兼容性极强。
五、小思考:邻接链表能解决哪些实际问题?
除了开头提到的地图导航,带权有向图 + 邻接链表的组合,还能应用在很多场景:
- 网络路由:路由器之间的数据包传输(有向:A 能发给 B,B 不一定能发给 A;权重:传输延迟)。
- 任务调度:项目中的任务依赖(有向:任务 A 完成后才能做任务 B;权重:任务耗时)。
- 金融交易:用户之间的转账记录(有向:A 转给 B;权重:转账金额)。
下次再遇到这类 "有方向、有数值、多节点" 的问题,不妨想想:是不是能用带权有向图和邻接链表来解决?
总结
带权有向图是建模复杂现实问题的 "利器",而邻接链表则是让这个 "利器" 高效运转的 "刀鞘"------ 它用灵活的链表结构,平衡了空间占用和操作效率,让图的存储和计算不再 "笨重"。
如果你动手实现了文中的代码,不妨试试修改边的数量、权重,或者添加 "查找指定边""删除顶点" 的功能,进一步解锁邻接链表的更多用法~