leetcode 2872. 可以被 K 整除连通块的最大数目困难

给你一棵 n 个节点的无向树，节点编号为 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 有一条边。

同时给你一个下标从 0 开始长度为 n 的整数数组 values ，其中 values[i] 是第 i 个节点的值。再给你一个整数 k 。

你可以从树中删除一些边，也可以一条边也不删，得到若干连通块。一个 连通块的值 定义为连通块中所有节点值之和。如果所有连通块的值都可以被 k 整除，那么我们说这是一个 合法分割 。

请你返回所有合法分割中，连通块数目的最大值 。

示例 1：

复制代码

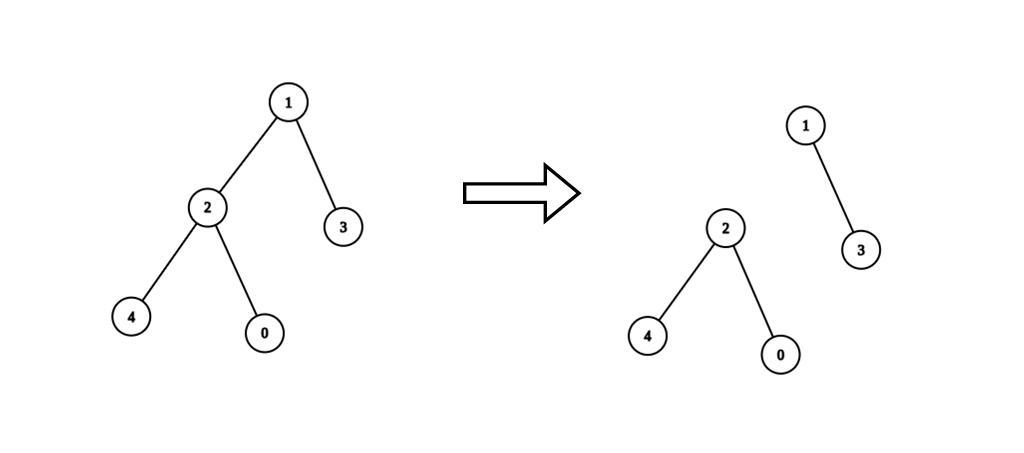
输入：n = 5, edges = [[0,2],[1,2],[1,3],[2,4]], values = [1,8,1,4,4], k = 6
输出：2
解释：我们删除节点 1 和 2 之间的边。这是一个合法分割，因为：
- 节点 1 和 3 所在连通块的值为 values[1] + values[3] = 12 。
- 节点 0 ，2 和 4 所在连通块的值为 values[0] + values[2] + values[4] = 6 。
最多可以得到 2 个连通块的合法分割。

示例 2：

复制代码

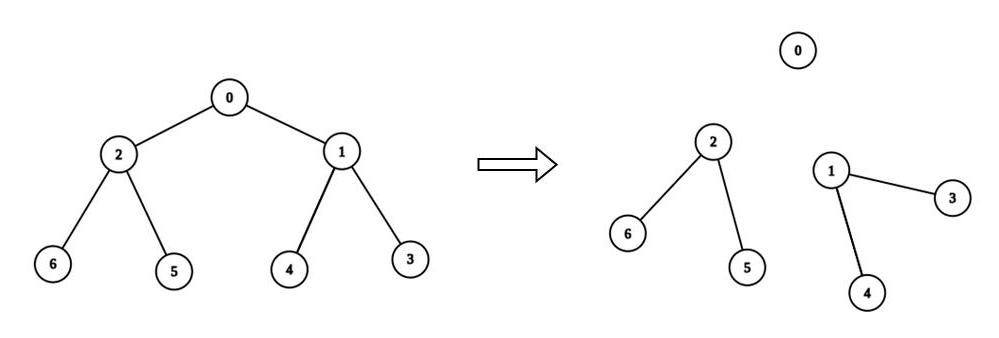
输入：n = 7, edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [3,0,6,1,5,2,1], k = 3
输出：3
解释：我们删除节点 0 和 2 ，以及节点 0 和 1 之间的边。这是一个合法分割，因为：
- 节点 0 的连通块的值为 values[0] = 3 。
- 节点 2 ，5 和 6 所在连通块的值为 values[2] + values[5] + values[6] = 9 。
- 节点 1 ，3 和 4 的连通块的值为 values[1] + values[3] + values[4] = 6 。
最多可以得到 3 个连通块的合法分割。

提示：

1 <= n <= 3 * 10^4
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
values.length == n
0 <= values[i] <= 10^9
1 <= k <= 10^9
values 之和可以被 k 整除。
输入保证 edges 是一棵无向树。

分析： 删除一条边后，一个连通块就分成了两个连通块。如果其中一个连通块的点权和不是 k 的倍数，那么这个连通块无论如何分割，始终存在一个点权和不是 k 的倍数的连通块。所以当且仅当这两个连通块的点权和都是 k 的倍数，这条边才能删除。删除后，由于分割出的连通块点权和仍然是 k 的倍数，所以可以继续分割，直到无法分割为止。换句话说，只要有能删除的边，就删除。

具体到实现上，可以从图上的任意一点开始 DFS，计算子树 x 的点权和 s。如果 s 是 k 的倍数，那么 x 到它的父节点的边可以删除。注意根节点没有父节点，为了代码的统一，可以新增一个点权为 0 的虚拟节点作为整棵树的根节点，它到编号为 0 的节点有一条边。最后的答案就是删除的边数 +1.

cpp 复制代码

class Solution {
public:    
    int ans=0;

    long long dfs(vector<vector<int>>&graph,vector<int>&values,int flag[],int ind,int k)
    {
        long long sum=0,temp=0;
        sum+=values[ind];flag[ind]=1;
        for(int i=0;i<graph[ind].size();++i)
        {
            if(!flag[graph[ind][i]])
            {
                flag[graph[ind][i]]=1;
                temp=dfs(graph,values,flag,graph[ind][i],k);
                flag[graph[ind][i]]=0;sum+=temp;
                
                if(temp%(k*1LL)==0)ans++;
            }
        }
        flag[ind]=0;
        return sum;
    }

    int maxKDivisibleComponents(int n, vector<vector<int>>& edges, vector<int>& values, int k) {
        vector<vector<int>>graph(n+5);
        for(int i=0;i<edges.size();++i)
        {
            graph[edges[i][0]].push_back(edges[i][1]);
            graph[edges[i][1]].push_back(edges[i][0]);
        }
        graph[n].push_back(0);graph[0].push_back(n);
        values.push_back(0);

        int flag[30010]={0};flag[n]=1;

        long long sum=0;
        sum=dfs(graph,values,flag,n,k);

        return ans;
    }
};

leetcode 2872. 可以被 K 整除连通块的最大数目 困难

leetcode 2872. 可以被 K 整除连通块的最大数目困难