20-Gradient Surgery for Multi-Task Learning

解决问题

在本文中，我们识别出多任务优化 landscape 中导致有害梯度干扰 的三个关键条件，并提出一种简单且通用的方法来避免任务梯度间的此类干扰。我们设计了一种梯度修正策略 ：对于存在梯度冲突的任意两个任务，将其中一个任务的梯度投影到另一个任务梯度的法平面上。在一系列具有挑战性的多任务监督学习和多任务强化学习问题中，该方法显著提升了学习效率和性能。此外，该方法具有模型无关性，可与现有多任务架构结合使用，进一步提升性能。

该方法的核心创新的是通过梯度投影消除冲突：对于任务 A 和任务 B，若梯度方向冲突（如夹角大于 90°），将任务 A 的梯度投影到任务 B 梯度的法平面上，得到新梯度 ------ 新梯度与任务 B 的梯度垂直，从而消除两者的冲突，让参数更新同时兼顾两个任务的优化需求。这种方式区别于 GradNorm 的 "梯度幅度调节"，更侧重 "梯度方向修正"，是解决梯度干扰的另一类核心思路。

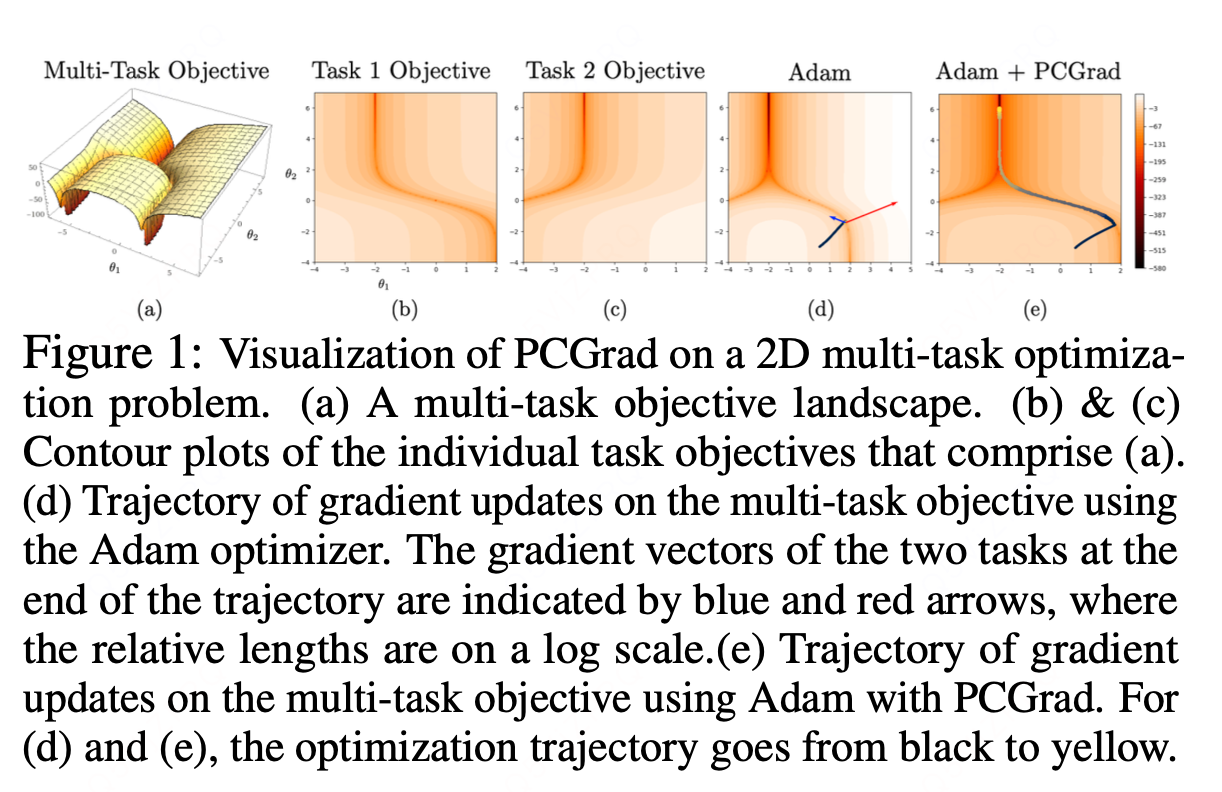
作为一个直观示例，我们来看图 1a-c 中两个任务目标的二维优化空间。每个任务的优化空间都包含一条深谷 ------ 这一特性已在神经网络优化空间的研究中被观察到 $22$ ，且每个谷底的特征是高正曲率 与任务梯度幅度的巨大差异。在这种情况下，多任务总梯度会被其中一个任务的梯度主导，而这会以牺牲另一个任务的性能为代价。此外，由于高曲率的存在，主导任务的性能提升可能被高估，而非主导任务的性能下降则可能被低估。最终，优化器难以在整体优化目标上取得实质性进展。在图 1d 中，优化器虽已抵达任务 1 的深谷，但在 "梯度冲突、高曲率、梯度幅度差异大" 的参数区域（见图 1d 中绘制的梯度），无法沿着谷道继续推进优化。在 5.3 节中，我们通过实验发现，这种 "悲剧三要素" 在高维神经网络多任务学习问题中同样存在。

方法

问题定义：

我们提出假设：多任务学习的核心优化问题源于冲突梯度------ 当不同任务的梯度内积为负时，表明它们方向相反（相互背离）。但冲突梯度本身并非有害：事实上，简单对任务梯度取平均，理论上应能获得多任务目标函数的最优下降方向。然而，在特定条件下，这类冲突梯度会导致性能显著下降。

以双任务优化问题为例：若一个任务的梯度幅度远大于另一个，前者会主导平均梯度；若任务梯度方向上同时存在高正曲率，则主导任务的性能提升可能被大幅高估，而非主导任务的性能下降可能被大幅低估。因此，我们将这三个条件的同时出现定义为 "悲剧三要素"（tragic triad），具体描述如下：(a) 多个任务的梯度存在冲突（方向相反）；(b) 梯度幅度差异显著，导致部分任务梯度主导全局；(c) 多任务优化空间存在高曲率。

以下是三个条件的形式化定义：

在优化过程中，PCGrad 通过以下简洁流程消除梯度冲突：若两个任务的梯度存在冲突（即余弦相似度为负），则将每个任务的梯度投影到另一个任务梯度的法平面上。这一操作本质是移除梯度中与其他任务冲突的分量，从而减少任务间的破坏性梯度干扰。该核心思想的可视化示意如图 2 所示。

PCGrad 多任务梯度修正的迭代流程与核心细节

PCGrad 会按以下方式完成所有任务的梯度修正，确保批次内任务间的梯度干扰最小化：

批次任务遍历逻辑 ：对于当前训练批次中的每个任务 $T_i$（目标任务），从批次内所有其他任务 $T_j$（$j \neq i$，共 $T-1$ 个任务，T 为批次内任务数）中随机采样并排序，按该随机顺序逐一处理每个 $T_j$。
迭代式梯度修正：对每个排序后的 $T_j$，执行 "冲突判断→投影修正" 的流程（前文步骤 1-2）：
- 首次处理 $T_j_1$ 时，用原始梯度 $\mathbf{g}i$ 与 $\mathbf{g}{j_1}$ 判断冲突，若冲突则投影修正，得到中间梯度 $\mathbf{g}_i^{(1)}$；
- 接着处理 $T_j_2$ 时，用更新后的 $\mathbf{g}i^{(1)}$ 与 $\mathbf{g}{j_2}$ 判断冲突，若冲突则继续投影修正，得到 $\mathbf{g}_i^{(2)}$；
- 重复该过程直至遍历所有 $T_j$，最终得到任务 $T_i$ 的最终修正梯度 $\mathbf{g}_i^{\text{PC}}$。
全批次任务覆盖：对当前批次中的每个任务（$T_1, T_2, ..., T_T$），均执行上述 "随机遍历其他任务→迭代修正" 的流程，最终得到所有任务的修正梯度 $\{\mathbf{g}_1^{\text{PC}}, \mathbf{g}_2^{\text{PC}}, ..., \mathbf{g}_T^{\text{PC}}\}$。
参数更新：将所有修正后的梯度传入优化器（如 Adam、SGD），按多任务损失的梯度加权规则（$\nabla L_{\text{total}} = \sum_i w_i \mathbf{g}_i^{\text{PC}}$，通常 $w_i=1$）更新共享网络参数。

实验结论：

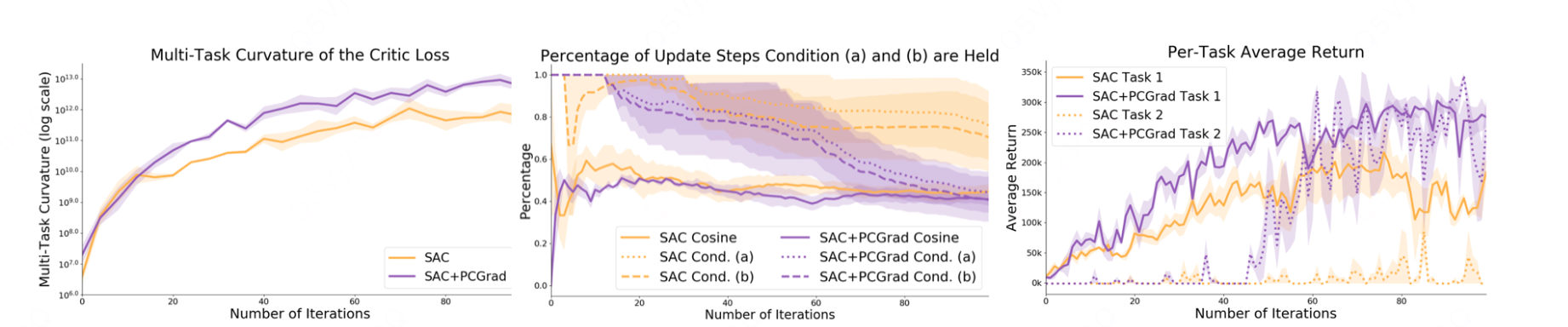
图 4：PCGrad 理论条件的实证分析（基于 RL 任务训练过程）

图 4 针对定理 2 中讨论的理论条件展开实证分析，展示了在两个强化学习任务（"reach（抓取）" 和 "press button top（按压顶部按钮）"）上训练前 100 轮的关键指标变化。

子图功能与结果解读

左图：多任务曲率的估计值

该图展示了训练过程中多任务曲率的动态变化，核心观察：训练全程均存在高多任务曲率。这为定理 2 中的条件（b）（高曲率）提供了直接实证支持 ------ 验证了 "悲剧三要素" 中的高曲率条件在实际多任务 RL 训练中持续存在，并非理论上的极端场景。

中图：梯度冲突与理论条件的满足比例

实线：两个任务梯度间余弦相似度为正的迭代轮次占比（即非冲突梯度的比例）；
虚线：在余弦相似度为负的迭代轮次中，定理 2 的条件（a）（梯度冲突） 成立的比例；
点划线：在余弦相似度为负的迭代轮次中，定理 2 条件（b）的推论（$\xi(\mathbf{g}_1, \mathbf{g}_2) \leq 1$） 成立的比例（$\xi$ 为梯度相关的辅助指标，具体定义见定理 2）。

核心观察：

对于 Adam 优化器（无 PCGrad）和 Adam+PCGrad 优化器，在尚未学会任务 2的阶段，条件（a）（梯度冲突）的满足比例始终处于高位（即梯度冲突频繁发生）；
一旦 Adam+PCGrad 开始学会任务 2（对应右图中任务 2 的回报上升），条件（a）的满足比例立即下降 ------ 说明 PCGrad 通过消除梯度冲突（打破条件（a）），推动了任务 2 的学习进程。

右图：SAC 与 SAC+PCGrad 的任务平均回报

该图对比了纯 SAC 算法与 SAC+PCGrad 算法在两个任务上的平均回报（回报越高，任务学习效果越好）：

纯 SAC 算法：任务 2 的回报长期处于低位，始终未能有效学会；
SAC+PCGrad 算法：训练后期任务 2 的回报显著上升，成功掌握任务，且任务 1 的回报未受影响（保持高位）。

核心结论与理论条件的关联

结合中图与右图的结果，可得出关键洞察：条件（a）（梯度冲突）是 PCGrad 在多任务学习中表现优异的核心原因------ 当梯度冲突频繁发生时（条件（a）成立比例高），纯 SAC 算法因冲突导致任务学习停滞；而 PCGrad 通过消除梯度冲突（降低条件（a）的成立比例），使任务 2 的学习取得实质性进展，最终实现多任务协同优化。