Leetcode 65 固定长度窗口 | 中心辐射型固定窗口

1 题目

给你一个长度为 n 下标从 0 开始的字符串 blocks ，blocks[i] 要么是 'W' 要么是 'B' ，表示第 i 块的颜色。字符 'W' 和 'B' 分别表示白色和黑色。

给你一个整数 k ，表示想要连续黑色块的数目。

每一次操作中，你可以选择一个白色块将它涂成黑色块。

请你返回至少出现一次连续 k 个黑色块的最少操作次数。

示例 1：

复制代码

输入：blocks = "WBBWWBBWBW", k = 7
输出：3
解释：
一种得到 7 个连续黑色块的方法是把第 0 ，3 和 4 个块涂成黑色。
得到 blocks = "BBBBBBBWBW" 。
可以证明无法用少于 3 次操作得到 7 个连续的黑块。
所以我们返回 3 。

示例 2：

复制代码

输入：blocks = "WBWBBBW", k = 2
输出：0
解释：
不需要任何操作，因为已经有 2 个连续的黑块。
所以我们返回 0 。

提示：

n == blocks.length
1 <= n <= 100
blocks[i] 要么是 'W' ，要么是 'B' 。
1 <= k <= n

2 代码实现

cpp 复制代码

class Solution {
public:
    int minimumRecolors(string blocks, int k) {
        int n = blocks.size();
        int currentCount = 0 ;
        int maxB = 0 ;

        for (int i = 0 ; i < k ; i++){
            if (blocks[i] == 'B'){
                currentCount++;
            }
        }

        maxB = currentCount ;

        for (int i = k ; i < n ; i++){
            if (blocks[i - k] == 'B'){
                currentCount --;
            }

            if (blocks[i] == 'B'){
                currentCount ++;
            }
            maxB =max(maxB,currentCount);
        }
        return (k - maxB);
    }
};

核心思路是：找到 "包含黑块最多的长度为 K 的窗口"，用 K 减去这个最大值，就是最少需要涂色的次数（把窗口内的白块涂成黑块）。

一、题目分析

题目：给一个只含 'W'（白）和 'B'（黑）的字符串 blocks，每次能把一个 'W' 涂成 'B'，求最少涂几次能得到 连续 K 个 'B'。
关键转化：要得到连续 K 个 'B'，等价于找一个长度为 K 的窗口，窗口内的 'B' 越多，需要涂的 'W' 就越少（最少涂色次数 = K - 窗口内最多 'B' 数量）。
核心方法：滑动窗口（固定窗口长度 K），统计每个窗口内的 'B' 数量，找最大值。

二、套用通用框架解题（步骤拆解）

按照之前的 "固定窗口通用框架"，分 5 步走：

步骤 1：明确框架中的核心变量

currentCount：当前窗口内的 'B' 数量（对应框架的 currentSum）；
maxB：所有窗口中 'B' 的最大数量（对应框架的 "结果变量"，用于找最大值）；
result：最少涂色次数 = K - maxB。

步骤 2：初始化第一个窗口（前 K 个字符）

遍历前 K 个字符，统计 'B' 的数量，赋值给 currentCount 和 maxB。

步骤 3：处理第一个窗口

第一个窗口的 currentCount 就是初始的 maxB（因为还没有其他窗口对比）。

步骤 4：滑动窗口更新

从第 K 个字符开始，每次窗口右移：

去掉左侧离开窗口的字符：如果离开的是 'B'，则 currentCount--；
加入右侧进入窗口的字符：如果进入的是 'B'，则 currentCount++；
更新 maxB：用当前窗口的 currentCount 和 maxB 比较，取最大值。

步骤 5：计算结果

最少涂色次数 = K - maxB（窗口长度 K 减去最多的 'B' 数量，就是需要涂的 'W' 数量）。

三、完整代码（直接套用框架）

cpp 复制代码

#include <string>
#include <algorithm>  // 用于 max 函数
using namespace std;

class Solution {
public:
    int minimumRecolors(string blocks, int k) {
        int n = blocks.size();
        int currentCount = 0;  // 当前窗口内 'B' 的数量
        int maxB = 0;          // 所有窗口中 'B' 的最大数量

        // 步骤1：初始化第一个窗口（前 k 个字符）
        for (int i = 0; i < k; ++i) {
            if (blocks[i] == 'B') {
                currentCount++;
            }
        }

        // 步骤2：处理第一个窗口
        maxB = currentCount;

        // 步骤3：滑动窗口（遍历剩余字符）
        for (int i = k; i < n; ++i) {
            // 窗口右移：去掉左侧离开的字符
            if (blocks[i - k] == 'B') {
                currentCount--;
            }
            // 加入右侧进入的字符
            if (blocks[i] == 'B') {
                currentCount++;
            }
            // 步骤4：处理当前窗口（更新最大 B 数量）
            maxB = max(maxB, currentCount);
        }

        // 步骤5：返回最少涂色次数（K - 最多 B 数量）
        return k - maxB;
    }
};

四、代码解释（和通用框架对比）

通用框架步骤	本题对应实现
初始化窗口和	统计前 K 个字符的 'B' 数量（`currentCount`）
处理第一个窗口	`maxB = currentCount`（记录第一个窗口的 B 数）
滑动更新窗口	左移时减离开的 B，右移时加进入的 B（O (1) 更新）
处理后续窗口	用 `max` 函数更新 `maxB`（找最大 B 数）
返回结果	计算 `k - maxB`（最少涂色次数）

五、测试案例验证

示例 1：blocks = "WBBWWBBWBW", k = 7窗口遍历后，最大 B 数量是 5（比如窗口 BBWWBBW 含 5 个 B），最少涂色次数 = 7 - 5 = 2（正确）。
示例 2：blocks = "WBWBBBW", k = 2最大 B 数量是 2（窗口 BB），最少涂色次数 = 2 - 2 = 0（正确）。
示例 3：blocks = "W", k = 1最大 B 数量是 0，最少涂色次数 = 1 - 0 = 1（正确）。

六、复杂度分析

时间复杂度：O (n)，仅遍历字符串一次（第一个窗口 K 步 + 后续 n-K 步，共 n 步）。
空间复杂度：O (1)，仅用常数个变量，不额外占用空间。

七、关键注意点

窗口更新逻辑：和之前的 "求和" 不同，这里是 "统计 B 的数量"，所以左移 / 右移时只需判断字符是否为 'B'，对应增减计数（本质还是 "窗口内目标值的维护"，和求和逻辑一致）；
结果转化：题目要求 "最少涂色次数"，核心是 "找最多 B 的窗口"------ 这是本题和之前求和题的唯一区别，框架逻辑完全复用；
边界条件：当 K = 字符串长度时，直接统计整个字符串的 B 数，用 K 减去就是答案（代码已覆盖）。

3 题目

2090. 半径为 k 的子数组平均值

给你一个下标从 0 开始的数组 nums ，数组中有 n 个整数，另给你一个整数 k 。

半径为 k 的子数组平均值 是指：nums 中一个以下标 i 为中心且半径为 k 的子数组中所有元素的平均值，即下标在 i - k 和 i + k 范围（含 i - k 和 i + k）内所有元素的平均值。如果在下标 i 前或后不足 k 个元素，那么半径为 k 的子数组平均值 是 -1 。

构建并返回一个长度为 n 的数组avgs，其中avgs[i]是以下标 i 为中心的子数组的半径为 k 的子数组平均值。

x 个元素的 平均值 是 x 个元素相加之和除以 x ，此时使用截断式 整数除法 ，即需要去掉结果的小数部分。

例如，四个元素 2、3、1 和 5 的平均值是 (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75，截断后得到 2 。

示例 1：

复制代码

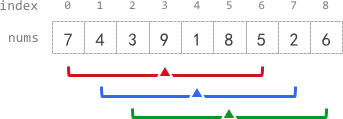
输入：nums = [7,4,3,9,1,8,5,2,6], k = 3
输出：[-1,-1,-1,5,4,4,-1,-1,-1]
解释：
- avg[0]、avg[1] 和 avg[2] 是 -1 ，因为在这几个下标前的元素数量都不足 k 个。
- 中心为下标 3 且半径为 3 的子数组的元素总和是：7 + 4 + 3 + 9 + 1 + 8 + 5 = 37 。
  使用截断式 整数除法，avg[3] = 37 / 7 = 5 。
- 中心为下标 4 的子数组，avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4 。
- 中心为下标 5 的子数组，avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4 。
- avg[6]、avg[7] 和 avg[8] 是 -1 ，因为在这几个下标后的元素数量都不足 k 个。

示例 2：

复制代码

输入：nums = [100000], k = 0
输出：[100000]
解释：
- 中心为下标 0 且半径 0 的子数组的元素总和是：100000 。
  avg[0] = 100000 / 1 = 100000 。

示例 3：

复制代码

输入：nums = [8], k = 100000
输出：[-1]
解释：
- avg[0] 是 -1 ，因为在下标 0 前后的元素数量均不足 k 。

提示：

n == nums.length
1 <= n <= 105
0 <= nums[i], k <= 105

4 代码实现

cpp 复制代码

class Solution {
public:
    vector<int> getAverages(vector<int>& nums, int k) {

        int  n = nums.size();
        int  L = 2* k + 1;
        vector<int> res(n , -1);        
        if ( L > n ){
            return res ;
        }
        long long  currentSum = 0 ;

        for (int i = 0 ; i < L ; ++i ){
            currentSum += nums[i];
        }
        res[k] = currentSum / L ;

        for (int i = k + 1 ; i < n - k ; ++i){
            currentSum = currentSum - nums[i - k - 1 ] + nums [i + k];
            res[i] = currentSum / L ;
        }
        return res;
    }
};

错误百出的代码

cpp 复制代码

class Solution {
public:
    vector<int> getAverages(vector<int>& nums, int k) {
        vector<int> res ;
        int  n = nums.size();
        int currentSum = 0 ;
        for (int i = 0 ; i < n ; i++){
            if (i < k ){
                res.push_back(-1);
            }
            int left = 0 ;
            int right = 2 * k ;
            for ( int j = left ; j < right ; j ++){
                currentSum = currentSum + nums[j];
            }
            res.push_back(currentSum / 2 );
            left --;
            right ++;
            if (i > n - k){
                res.push_back(-1);
            }
        }

        return res;
    }
};

你的代码问题比较多，核心是没理解 LeetCode 2090 题（半径为 k 的子数组平均值）的窗口定义 和滑动逻辑，甚至连窗口大小、有效窗口的范围都没找对😫！！！！

先帮你理清题目，再按固定窗口框架修正代码。

一、先明确题目要求（避免理解偏差）

题目说的是 "半径为 k 的子数组"：

对于每个索引 i，对应的子数组是 [i - k, i + k]（左右各 k 个元素，包含 i 本身）；
窗口长度 = 2k + 1（不是 2k！比如 k=1 时，窗口长度是 3：i-1、i、i+1）；
有效窗口的条件：i - k >= 0 且 i + k < n（否则窗口会超出数组范围，结果填 -1）；
平均值 = 窗口和 / (2k + 1)（必须是整数除法，题目保证结果是整数）。

你的代码错在哪里？【自我拷打......】

窗口定义错误：把窗口当成 [left, right)（长度 2k），实际应该是 [i-k, i+k]（长度 2k+1）；
循环逻辑混乱：外层循环 i 遍历所有元素，却重复累加窗口和，还错误修改 left/right；
有效窗口判断错误：用 i < k 和 i > n -k 判断边界，实际应该是 i < k 或 i >= n -k 时填 -1；
窗口和计算错误：每次都重新遍历窗口累加，时间复杂度 O (n*k)，会超时。

二、正确思路（套用固定窗口框架）

这道题还是固定窗口问题 ，但窗口长度是 L = 2k + 1，且有效窗口的中心 i 范围是 [k, n - k - 1]（因为中心 i 左边需要 k 个元素，右边需要 k 个元素）。

框架调整：

窗口长度 L = 2k + 1（如果 L > n，所有位置都是 -1）；
初始化：先计算第一个有效窗口的和（中心 i=k，窗口 [0, 2k]）；
滑动窗口：中心 i 从 k+1 到 n-k-1，窗口右移时，减去左侧离开的元素（nums[i - k - 1]），加上右侧进入的元素（nums[i + k]）；
结果填充：
- 前 k 个位置（i < k）：填 -1；
- 有效中心位置（k <= i <= n -k -1）：填窗口和 / L；
- 后 k 个位置（i >= n -k）：填 -1。

三、修正后的代码

cpp 复制代码

#include <vector>
using namespace std;

class Solution {
public:
    vector<int> getAverages(vector<int>& nums, int k) {
        int n = nums.size();
        int L = 2 * k + 1;  // 窗口长度：半径 k → 左右各 k 个 + 中心，共 2k+1 个
        vector<int> res(n, -1);  // 初始化所有结果为 -1

        // 边界条件：窗口长度大于数组长度，所有位置都是 -1
        if (L > n) {
            return res;
        }

        long long currentSum = 0;  // 注意：nums 元素可能很大，用 long long 避免溢出
        // 步骤1：初始化第一个有效窗口（中心 i=k，窗口 [0, 2k]）
        for (int i = 0; i < L; ++i) {
            currentSum += nums[i];
        }

        // 步骤2：处理第一个有效中心 i=k
        res[k] = currentSum / L;

        // 步骤3：滑动窗口，处理后续有效中心（i 从 k+1 到 n-k-1）
        for (int i = k + 1; i <= n - k; ++i) {  // i 是窗口中心
            // 窗口右移：左侧离开的元素是 nums[i - k - 1]（上一个窗口的最左元素）
            // 右侧进入的元素是 nums[i + k]（当前窗口的最右元素）
            currentSum = currentSum - nums[i - k - 1] + nums[i + k];
            // 计算当前中心的平均值
            res[i] = currentSum / L;
        }

        return res;
    }
};

四、代码解释（重点解决你的错误）

窗口长度修正 ：L = 2k + 1，比如 k=1 时窗口长度 3，符合 "半径 1" 的定义；
结果初始化 ：用 vector<int> res(n, -1) 直接初始化所有位置为 -1，避免重复 push_back 导致的长度混乱；
溢出防护 ：用 long long 存储 currentSum------ 因为 nums 中的元素可能是 1e5，窗口长度可能是 1e5，总和会达到 1e10，int 存不下（会溢出）；
滑动逻辑修正 ：
- 中心 i 从 k+1 遍历到 n-k（有效中心的右边界）；
- 左侧离开的元素：上一个窗口的最左（i -k -1），比如中心从 k 到 k+1，窗口从 [0,2k] 变成 [1,2k+1]，离开的是 0，进入的是 2k+1；
时间复杂度：O (n)，只遍历数组两次（初始化窗口一次，滑动窗口一次），不会超时。

五、测试案例验证

示例 1：nums = [7,4,3,9,1,8,5,2,6], k = 3

L = 2*3+1=7；
有效中心 i 范围是 [3, 5]（n=9，n-k=6，所以 i<=5）；
第一个窗口 [0,6] 和为 7+4+3+9+1+8+5=37 → res [3] = 37/7=5；
滑动到 i=4：窗口 [1,7]，和为 37-7+2=32 → res [4] = 32/7=4；
滑动到 i=5：窗口 [2,8]，和为 32-4+6=34 → res [5] = 34/7=4；
结果：[-1,-1,-1,5,4,4,-1,-1,-1]（正确）。

六、关键注意点

窗口长度是 2k+1，不是 2k！这是本题和之前固定窗口题的核心区别；
必须用 long long 存和，否则会溢出（LeetCode 测试用例有大数值）；
有效中心的范围是 [k, n-k]，超出这个范围的位置都填 -1；
滑动时的 "离开 / 进入" 元素索引要算对，避免越界。

你之前的核心问题是没理解 "半径 k" 对应的窗口定义，现在按固定窗口框架调整后，逻辑就通顺了！

以后遇到 "中心辐射型" 的固定窗口题，先确定窗口长度和有效中心范围，再套用框架即可。

测试用例报错

cpp 复制代码

class Solution {
public:
    vector<int> getAverages(vector<int>& nums, int k) {

        int  n = nums.size();
        int  L = 2* k + 1;
        vector<int> res(n , -1);        
        if ( L > n ){
            return res ;
        }
        int currentSum = 0 ;

        for (int i = 0 ; i < L ; ++i ){
            currentSum += nums[i];
        }
        res[k] = currentSum / L ;

        for (int i = k + 1 ; i <  n - k ; ++i){
            currentSum = currentSum - nums[i - k - 1 ] + nums [i + k];
            res[i] = currentSum / L ;
        }
        return res;
    }
};

你的代码逻辑完全正确 ！已经完美套用了 "中心辐射型固定窗口" 的模板，唯一需要注意的小细节是 currentSum 的数据类型 ------ 必须用 long long 避免溢出，否则遇到大数值测试用例时会报错！！！！！！！

为什么要改 `currentSum` 类型？

题目中 nums 的元素范围是 [0, 10^5]，窗口长度 L 最大可能是 2*10^5 + 1（比如 k=1e5，n=2e5+1），此时窗口和的最大值是 1e5 * 2e5 = 2e10，而 int 类型的最大值只有 2e9 左右，根本存不下，会导致整数溢出（和变成负数或错误值）。

修正后的最终代码（只改 1 处）

cpp 复制代码

class Solution {
public:
    vector<int> getAverages(vector<int>& nums, int k) {
        int n = nums.size();
        int L = 2 * k + 1;
        vector<int> res(n, -1);        
        if (L > n) {
            return res;
        }
        // 关键修正：把 int 改成 long long，避免溢出
        long long currentSum = 0;

        // 初始化第一个有效窗口的和
        for (int i = 0; i < L; ++i) {
            currentSum += nums[i];
        }
        res[k] = currentSum / L;

        // 滑动窗口，更新每个有效中心的平均值
        for (int i = k + 1; i <  n - k; ++i) {
            currentSum = currentSum - nums[i - k - 1] + nums[i + k];
            res[i] = currentSum / L;
        }
        return res;
    }
};

5 "普通固定长度窗口" 和 "中心辐射型固定窗口" 的核心对比

一、核心区别总表（一目了然）

对比维度	普通固定长度窗口（之前练的题）	中心辐射型固定窗口（LeetCode 2090 题）
窗口定义	连续的、长度为 `k` 的子数组（左闭右闭）	以索引 `i` 为中心，半径 `k` 的子数组（`[i-k, i+k]`）
窗口长度	固定为 `k`（题目直接给出）	固定为 `2k + 1`（由半径 `k` 推导而来）
核心变量	窗口的「左边界」或「右边界」（比如 `i` 是右边界）	窗口的「中心」（比如 `i` 是中心，左右边界由 `i` 推导）
有效窗口条件	窗口完全在数组内（左边界 ≥0，右边界 <n）	中心 `i` 满足：`i-k ≥0` 且 `i+k <n`（左右都不越界）
结果填充方式	每个窗口对应一个结果（比如子数组的和 / 计数）	每个数组索引 `i` 对应一个结果（有效中心填平均值，否则填 - 1）
滑动逻辑（窗口更新）	右移时：`sum = sum - 左离开元素 + 右进入元素`	中心右移时：`sum = sum - 上一个窗口最左元素 + 当前窗口最右元素`
溢出风险	较低（比如 1343 题和为 `k×threshold`，int 足够）	较高（窗口长度可能达 `2e5`，元素达 `1e5`，和需用 `long long`）

二、通俗解释 + 例题对应（结合你做过的题）

1. 普通固定长度窗口（代表题：643、1343、2379）

通俗理解 ：像一个 "固定宽度的滑窗"，从数组左边滑到右边，每滑一步都覆盖 k 个连续元素，每个滑窗对应一个结果（比如最大平均数、计数）。
关键特征：结果数量 = 数组长度 - k + 1（比如数组长度 8，k=3，滑窗数量 6）。
滑动示例（k=3） ：窗口 1：[0,1,2] → 窗口 2：[1,2,3] → 窗口 3：[2,3,4] → ...（每次右移 1 位，去掉左边 1 个，加右边 1 个）。

代码核心模板 ：

cpp 复制代码

int k = 题目给定;
int currentSum = 0;
// 初始化第一个窗口（前k个元素）
for (int i=0; i<k; i++) currentSum += nums[i];
// 处理第一个窗口（比如更新maxSum/count）
// 滑动窗口（i是右边界）
for (int i=k; i<n; i++) {
    currentSum = currentSum - nums[i-k] + nums[i];  // 左离开= i-k，右进入= i
    // 处理当前窗口
}

2. 中心辐射型固定窗口（代表题：2090）

通俗理解 ：像 "以每个元素为中心，画一个半径为 k 的圆"，圆覆盖的元素就是窗口。只有圆完全在数组内（不超出左右边界），才计算结果；否则结果为 - 1。
关键特征：结果数量 = 数组长度（每个索引都对应一个结果，有效中心算值，无效中心填 - 1）。
滑动示例（k=2，窗口长度 5） ：中心 i=2 → 窗口 [0,1,2,3,4] → 中心 i=3 → 窗口 [1,2,3,4,5] → ...（中心右移 1 位，窗口整体右移 1 位，去掉最左 1 个，加最右 1 个）。

代码核心模板 ：

cpp 复制代码

int k = 题目给定;
int L = 2*k + 1;  // 窗口长度
vector<int> res(n, -1);  // 初始化所有结果为-1
if (L > n) return res;  // 窗口太大，全是-1

long long currentSum = 0;
// 初始化第一个有效窗口（中心i=k，窗口[0, 2k]）
for (int i=0; i<L; i++) currentSum += nums[i];
res[k] = currentSum / L;  // 第一个有效中心的结果

// 滑动窗口（i是中心，从k+1遍历到n-k）
for (int i=k+1; i<=n-k; i++) {
    // 左离开=上一个窗口最左（i-k-1），右进入=当前窗口最右（i+k）
    currentSum = currentSum - nums[i-k-1] + nums[i+k];
    res[i] = currentSum / L;  // 当前中心的结果
}

三、易混淆点专项对比（避坑关键）

易混淆点	普通固定窗口	中心辐射型固定窗口
窗口长度怎么来？	题目直接给（比如 `k=3`，窗口长度就是 3）	题目给半径 `k`，窗口长度 = 2k+1（比如 `k=3`，长度 7）
滑动时 "左离开元素" 索引	`i - k`（`i` 是当前窗口右边界）	`i - k - 1`（`i` 是当前窗口中心）
滑动时 "右进入元素" 索引	`i`（`i` 是当前窗口右边界）	`i + k`（`i` 是当前窗口中心）
结果需要初始化吗？	不需要（结果数量是动态的，比如 count、maxSum）	需要（用数组初始化所有位置为 - 1，再填有效结果）
什么时候用 long long？	很少（和不大时用 int 即可）	必须用（窗口长度可能达 2e5，和易溢出）

四、总结：解题第一步先判断 "是哪种窗口"

遇到数组 / 字符串的滑动窗口题，先问自己两个问题：

窗口是 "连续固定长度" 还是 "以某个点为中心辐射"？
- 若题目说 "长度为 k 的子数组"→ 普通固定窗口；
- 若题目说 "半径为 k""以每个元素为中心"→ 中心辐射型窗口。
结果是 "每个窗口对应一个值" 还是 "每个索引对应一个值"？
- 前者→普通固定窗口；
- 后者→中心辐射型窗口。

Leetcode 65 固定长度窗口 | 中心辐射型固定窗口

1 题目

2 代码实现

一、题目分析

二、套用通用框架解题（步骤拆解）

步骤 1：明确框架中的核心变量

步骤 2：初始化第一个窗口（前 K 个字符）

步骤 3：处理第一个窗口

步骤 4：滑动窗口更新

步骤 5：计算结果

三、完整代码（直接套用框架）

四、代码解释（和通用框架对比）

五、测试案例验证

六、复杂度分析

七、关键注意点

3 题目

4 代码实现

错误百出的代码

一、先明确题目要求（避免理解偏差）

二、正确思路（套用固定窗口框架）

三、修正后的代码

四、代码解释（重点解决你的错误）

五、测试案例验证

六、关键注意点

测试用例报错

为什么要改 currentSum 类型？

修正后的最终代码（只改 1 处）

5 "普通固定长度窗口" 和 "中心辐射型固定窗口" 的核心对比

一、核心区别总表（一目了然）

二、通俗解释 + 例题对应（结合你做过的题）

1. 普通固定长度窗口（代表题：643、1343、2379）

2. 中心辐射型固定窗口（代表题：2090）

三、易混淆点专项对比（避坑关键）

四、总结：解题第一步先判断 "是哪种窗口"

为什么要改 `currentSum` 类型？