
◆ 博主名称: 小此方-CSDN博客
大家好,欢迎来到晓此方的博客。
⭐️个人专栏:《C语言》_小此方的博客-CSDN博客
⭐️踏破千山志未空,拨开云雾见晴虹。 人生何必叹萧瑟,心在凌霄第一峰。
目录
1.1.6加餐内容二:通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
[2.1.3 对应到代码逻辑](#2.1.3 对应到代码逻辑)
前面我们了解到:满二叉树和完全二叉树由于其物理连续性可以使用数组来存储,然而,二叉树不只有这些特殊情况。对于一般的二叉树,我们只能使用链式结构进行存储。这样的二叉树:我们称之为------链式二叉树。
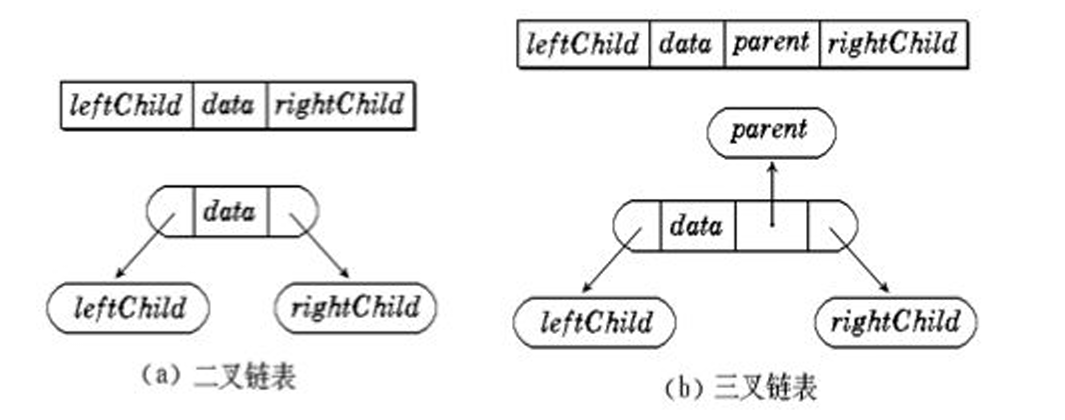
链式二叉树有三叉链和二叉链两种常见形式,但是二叉链式更加常见------以下我们的讨论主要集中在二叉链。
一,二叉树的遍历
1.1前序/中序/后序遍历
学习二叉树结构,最简单的一步就是遍历 。所谓二叉树遍历 (Traversal)是按照某种特定的规则,依次对二叉 树中的结点进行相应的操作,并且每个结点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
1.1.1二叉树的遍历有:前序/中序/后序的递归结构遍历
-
前序遍历(Preorder Traversal 亦称先序遍历)------访问根结点的操作发生在遍历其左右子树之前。
-
中序遍历(Inorder Traversal)------访问根结点的操作发生在遍历其左右子树之中(间)。
-
后序遍历(Postorder Traversal)------访问根结点的操作发生在遍历其左右子树之后。
1.1.3代码实现
cpp
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
printf("%c", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
cpp
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreePrevOrder(root->_left);
printf("%c", root->_data);
BinaryTreePrevOrder(root->_right);
}
cpp
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
printf("%c", root->_data);
}很多人看到这几行代码后一脸懵。递归确实不好理解。
下面主要用递归展开图分析前序递归遍历,帮助你更好理解递归遍历。(中序与后序图解类似)
1.1.3前序遍历递归图解
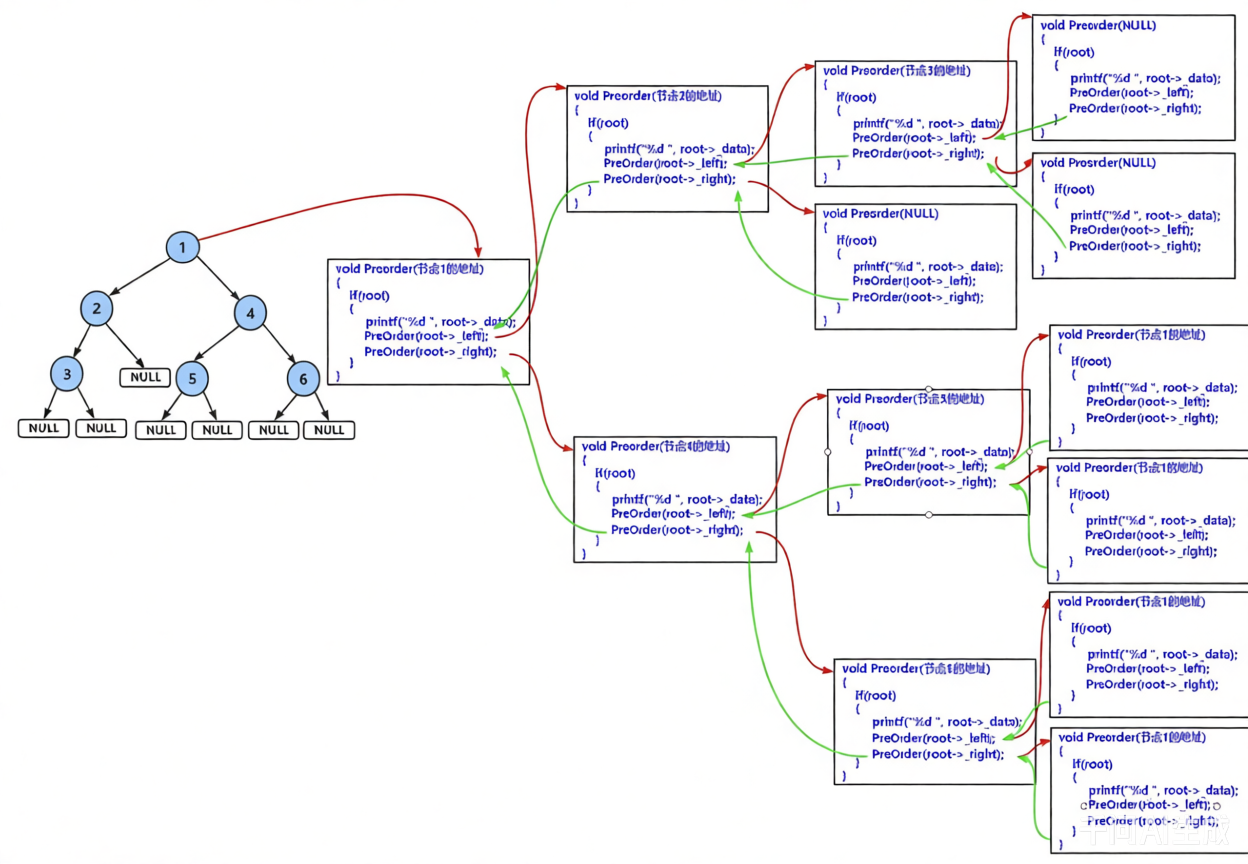
如图详细解释了前序遍历递归调用的过程。
1,整个过程从根节点 开始,遵循"根 → 左 → 右"的顺序访问每个节点。
2,图中左侧为二叉树结构,右侧则展示了相应的递归函数调用栈。
3,红色箭头指示了进入子函数调用的方向,而绿色箭头则表示函数执行完毕后的返回路径。
4,最终,按照前序遍历规则,节点被依次访问并打印出:1, 2, 3, 4, 5, 6。
1.1.4误区解释
很多人在学习这三大遍历的时候都会犯的错误:只记住遍历结果的"数值序列",却忽略了递归过程中对NULL节点的处理。
前序遍历结果:1 2 3 4 5 6
中序遍历结果:3 2 1 5 4 6
后序遍历结果:3 2 5 6 4 1
表面上是正确的,但是可能没有真正理解前序中序后序遍历
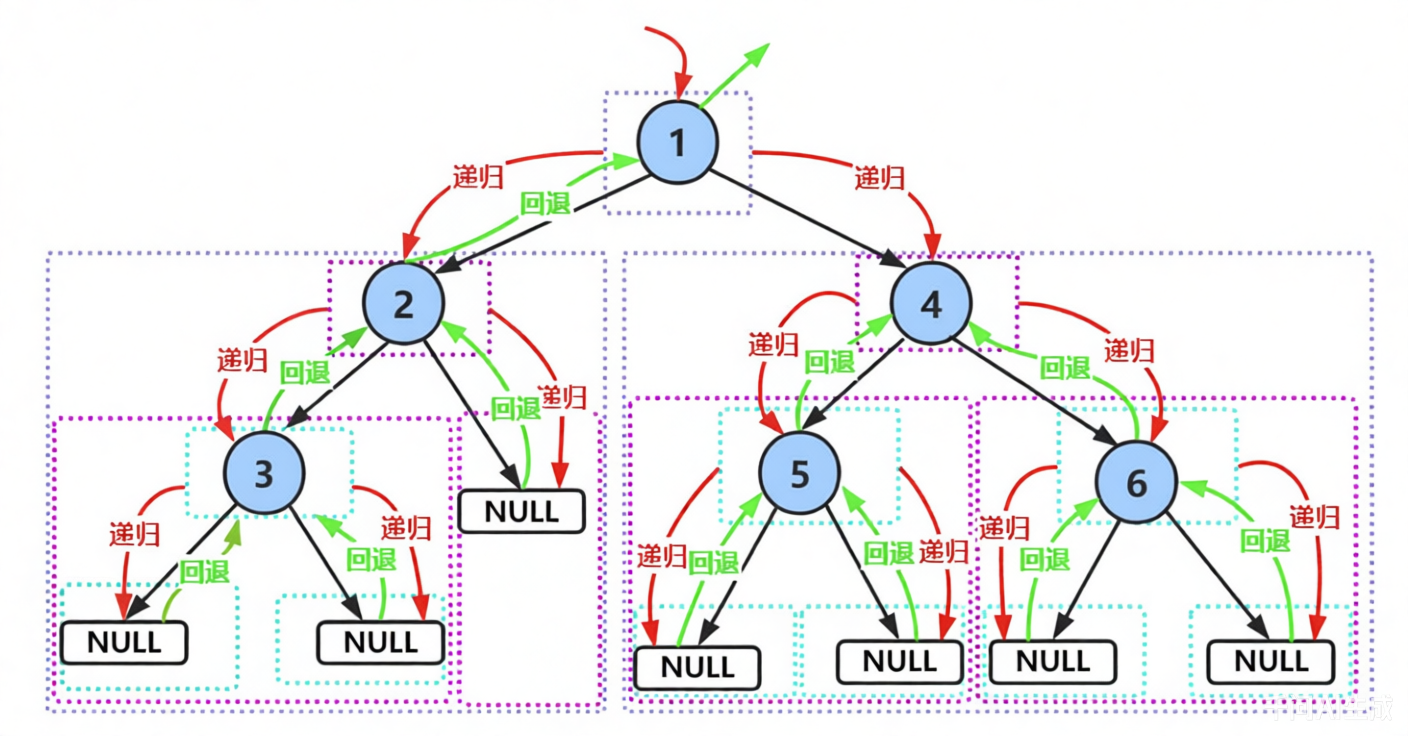
但如果深入理解递归过程,我们会发现:每次访问一个节点时,程序都会尝试进入其左右子树。
如图所示:当递归执行到节点 3 时,函数仍会继续递归调用其左子树(空指针),然后立刻返回;同理,右子树也如此。
因此,在完整追踪所有调用路径的前提下,真正的遍历轨迹应包含**NULL** 的访问行为。即使子树为空,也会触发一次"递归调用"并立即返回。因此我们得到这三者遍历的实际结果应该是:
前序遍历结果:1,2,3,N,N,N,4,5,N,N,6,N,N
中序遍历结果:N,3,N,2,N,1,N,5,N,4,N,6,N
后序遍历结果:N,N,3,N,2,N,N5,N,N,6,4,1
1.1.5加餐内容1:利用前中后序的文字结果还原二叉树
1.1.5.1前序和后序的作用:找根

如图所示,在前序序列 1,2,3,N,N,N,4,5,N,N,6,N,N 中,第一个数字 1 即为根节点。后续的子序列可以按此原则递归划分。
1.1.5.2中序的作用:找左右

在中序序列 N,3,N,2,N,1,N,5,N,4,N,6,N 中,根节点**1** 出现的位置将序列分为两部分:
- 左侧:
N,3,N,2,N→ 对应左子树 - 右侧:
N,5,N,4,N,6,N→ 对应右子树
结合前序/后序中根的信息,即可递归地构建出完整的树形结构。
1.1.6加餐内容二:通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
cpp
BTNode* BinaryTreeCreate(BTDataType* a,int* pi)
{
if (*(a + *pi) == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->_data = *(a + *pi);
(*pi)++;
root->_left=BinaryTreeCreate(a, pi);
root->_right=BinaryTreeCreate(a, pi);
return root;
}1.1.6.2执行流程详解
| 步骤 | 当前字符 | 操作 |
|---|---|---|
| 1 | 'A' |
创建根节点 A,继续处理左子树 |
| 2 | 'B' |
创建 B,其左子树为 # → 返回 NULL;右子树为 D |
| 3 | 'D' |
创建 D,左右均为 # → 成为叶子节点 |
| 4 | 'E' |
创建 E,左子树为 #,右子树为 H |
| 5 | 'H' |
创建 H,左右均为 # → 叶子节点 |
| 6 | 'C' |
创建 C,左子树为 F,右子树为 G |
| 7 | 'F' |
创建 F,左右均为 # → 叶子节点 |
| 8 | 'G' |
创建 G,左右均为 # → 叶子节点 |
其核心在于:
"先创建当前节点,再递归构建其左右子树。"
这是一种典型的自顶向下递归构造策略,广泛应用于树的序列化与反序列化场景。
1.2层序遍历
1.2.1性质
层序遍历是一种迭代遍历而不是递归遍历。
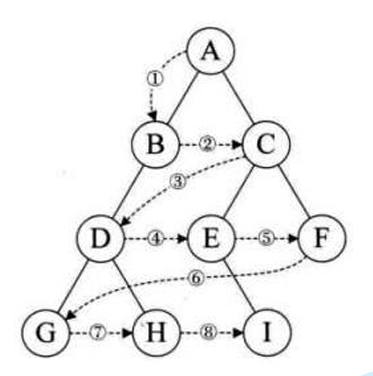
1.2.2操作方法
1,设二叉树的根结点所在层数为1。
2,从所在二叉树的根结点出发,首先访问第一层的树根结点。
3,然后从左到右访问第2层 上的结点,接着是第三层的结点。
4,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
1.2.3代码实现
cpp
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%c ", front->_data);
QueuePop(&q);
if (front->_left) {
QueuePush(&q, front->_left);
}
if (front->_right) {
QueuePush(&q, front->_right);
}
}
QueueDestroy(&q);
}1.2.3.1底层逻辑:
与递归遍历不同,层序遍历使用队列做为中介缓冲 ,利用父亲结点带动子节点入队的特性实现。
1.2.3.2核心思想:
- 利用队列的 先进先出(FIFO) 特性。
- 每一层的节点依次入队,并在出队时将其子节点按顺序加入队列,从而实现逐层遍历。
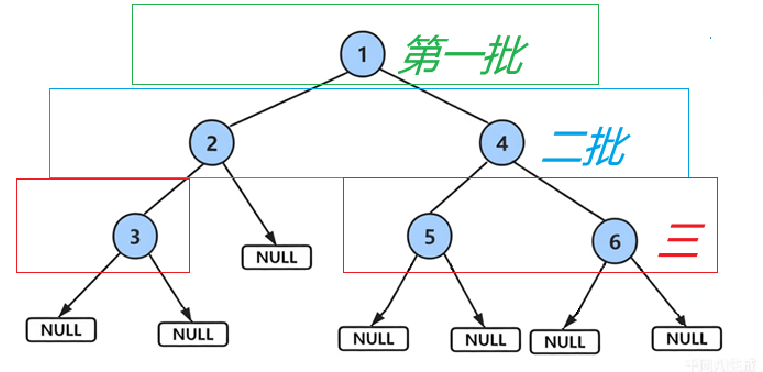
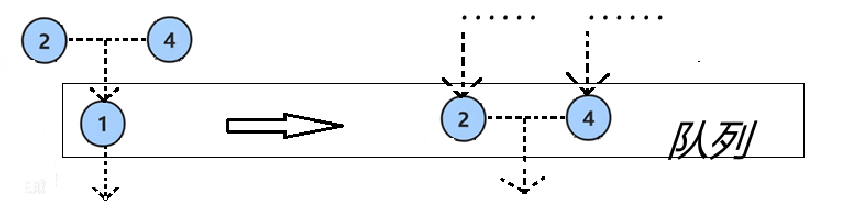
- 第一批 :根节点
1入队。 - 第二批 :
1出队后,其左右子节点2和4入队。 - 第三批 :
2出队后,其左子节点3入队;4出队后,其左右子节点5和6入队。 - 以此类推,逐层扩展
<操作流程>
初始状态:队列为空 步骤1:将根节点 1 入队 → 队列: [1] ↓
步骤2:取出 1,打印并将其子节点 2, 4 入队 → 队列: [2, 4] ↓
步骤3:取出 2,打印并将其子节点 3 入队 → 队列: [4, 3] ↓
步骤4:取出 4,打印并将其子节点 5, 6 入队 → 队列: [3, 5, 6] ↓
步骤5:取出 3,无子节点 → 队列: [5, 6] ↓ ...
二,二叉树的结点个数
2.1二叉树的总结点个数
cpp
int binarytreesize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return binarytreesize(root->_left) + binarytreesize(root->_right) + 1;
}代码简洁明了,但其背后蕴含着深刻的递归思维------"分而治之"与"层层上报"。
首先我来举一个常见的例子:
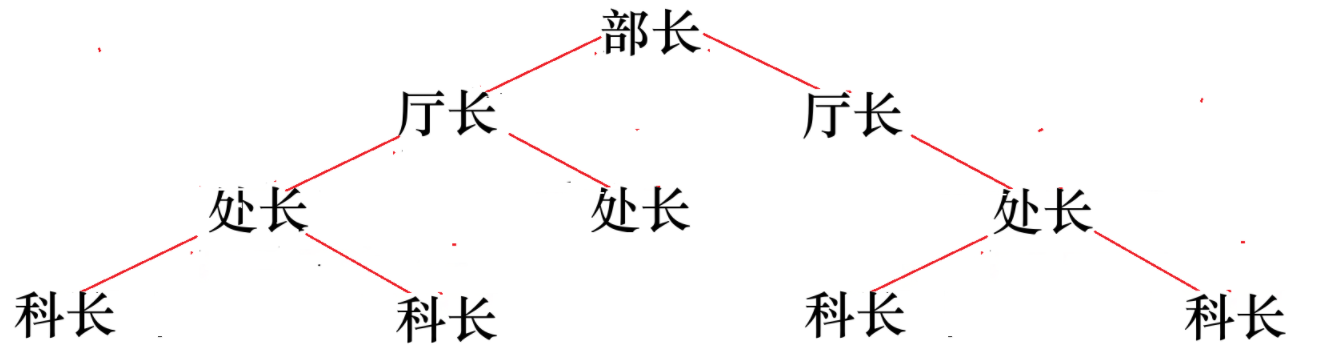
2.1.1递推过程:分而治之
省部级领导需要了解本省的干部总人数,于是向下派发任务:
- 要求每个"厅长"统计自己管辖范围内(包括下属)的所有人员数量。
- "厅长"再将任务下派给各自的"处长"。
- "处长"继续将任务交给"科长"。
- 最终,任务逐层下放到最基层的"科长"。
2.1.2回归过程:层层上报
- 基层执行:每个"科长"没有下属,因此直接报告:"我有 1 人。"
- 逐级汇总 :
- "处长"收到两个"科长"的汇报后,计算**:
1 + 1 + 1 = 3**(两个下属 + 自己)。 - "厅长"收到两个"处长"的结果后,计算**:
3 + 3 + 1 = 7**。 - "部长"汇总两个"厅长"的数据**:
7 + 7 + 1 = 15**。
- "处长"收到两个"科长"的汇报后,计算**:
最终结果:整个组织共有 15 名干部。
2.1.3 对应到代码逻辑
| 组织角色 | 代码对应 | 功能 |
|---|---|---|
| 科长(叶子节点) | root == NULL |
返回 0;无子节点,不参与计数 |
| 处长、厅长、部长 | 递归调用 | 向下分发任务,向上汇总结果 |
递归本质:
- 分解:将大问题拆解为子问题(每个子树的节点数)。
- 合并:子问题的结果相加,并加上当前节点本身(+1)。
- 终止条件:空指针(NULL)表示无节点,返回 0。
2.2二叉树的叶子结点个数
趁热打铁,我们来看一下叶子节点个数的计算方式
cpp
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if ( root->_left == NULL&&root->_right==NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}与"总结点个数"的递归思路类似,但有一个关键区别:
- 总结点个数:每个节点都算一次(+1),包括非叶子节点。
- 叶子节点个数 :只统计那些左右子树都为空的节点。
省部级领导现在只想知道有多少位"科长"------也就是最基层的干部(叶子节点)。
- 科长(叶子节点) :
- 没有下属,直接报告:"我是科长,我是一个叶子。" → 返回
1。
- 没有下属,直接报告:"我是科长,我是一个叶子。" → 返回
- 处长 :
- 有两个"科长"下属,分别汇报结果:
1和1。 - 自己不是叶子,不计入,只需将两个子树的结果相加 →
1 + 1 = 2。
- 有两个"科长"下属,分别汇报结果:
- 厅长 :
- 有两个"处长",各返回
2,所以总和为2 + 2 = 4。
- 有两个"处长",各返回
- 部长 :
- 两个"厅长"各返回
4,最终结果为4 + 4 = 8。
- 两个"厅长"各返回
最终结果 :共有 8 位科长,即 8 个叶子节点。
2.3计算第k层结点的个数
相比前两个问题,本题的递归逻辑更加复杂,需要引入一个额外参数 k 来追踪当前所在的层级 。我们通过"层层递减"的方式,精准定位目标层的节点数量。
cpp
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (k == 1)
{
return 1;
}
else
{
k--;
}
return BinaryTreeLevelKSize(root->_left, k)+BinaryTreeLevelKSize(root->_right, k);
}- 用
k表示当前目标层数。 - 每向下一层递归,
k就减 1,直到k == 1时,表示当前节点正好位于目标层。 - 此时返回
1,表示该节点是目标层的一个有效节点。
注意:
- 如果
k < 1,说明已经超出树的深度,应返回0。- 但为了简化边界处理,通常在调用时保证
k >= 1。
省部级领导现在想知道有多少位"处长 "------也就是权力体系中的第三层干部(k = 3)
部长(第1层)
- 目标是找第 3 层的节点 → 当前
k = 3 - 不是目标层,需向下查找 →
k--,变为k = 2
厅长(第2层)
- 找
k = 2层的节点 - 不是目标层,继续向下 →
k--,变为k = 1
处长(第3层)
- 找
k = 1层的节点 - 此时
k == 1,说明到达目标层,节点返回1
| 步骤 | 说明 |
|---|---|
if (k == 1) |
判断是否到达目标层,若是,则返回 1 |
k-- |
向下一层递归时,层数减 1 |
return left + right |
汇总左右子树中第 k 层的节点总数 |
关键技巧:
- 递归过程中,
k是"倒计时器":每深入一层,就减 1。 - 只有当
k == 1时,当前节点才被计入结果。 - 这种"递减计数"的方式,巧妙地实现了对特定层级的精确控制。
这个函数展示了递归中状态传递的强大能力:
"我不关心自己是不是目标层,我只负责把'还有几层'的信息传下去,直到有人找到答案。"
三,二叉树的查找
在实际应用中,我们常常需要在二叉树中查找某个特定值的节点。
cpp
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->_data == x)
{
return root;
}
BTNode* ret1 = BinaryTreeFind(root->_left, x);
if (ret1)
{
return ret1;
}
return BinaryTreeFind(root->_right, x);
}3.1采用模式:
- 逐层向下搜索:从根节点开始,依次检查左子树和右子树。
- 一旦找到即返回:只要在任意子树中找到了目标节点,就立即返回结果,不再继续搜索其他分支。
- 短路机制:利用"提前返回"避免不必要的遍历
3.2代码逻辑
| 步骤 | 说明 |
|---|---|
if (root == NULL) |
边界条件:空树无节点可查,返回 NULL |
if (root->_data == x) |
当前节点匹配目标值 → 返回当前节点指针 |
ret1 = BinaryTreeFind(root->_left, x) |
递归搜索左子树 |
if (ret1 != NULL) |
若左子树找到,则直接返回结果(短路) |
return BinaryTreeFind(root->_right, x) |
左边没找到,再去右边找 |
四,判断是否是完全二叉树
这应该是二叉树中最难的部分
4.1思路介绍
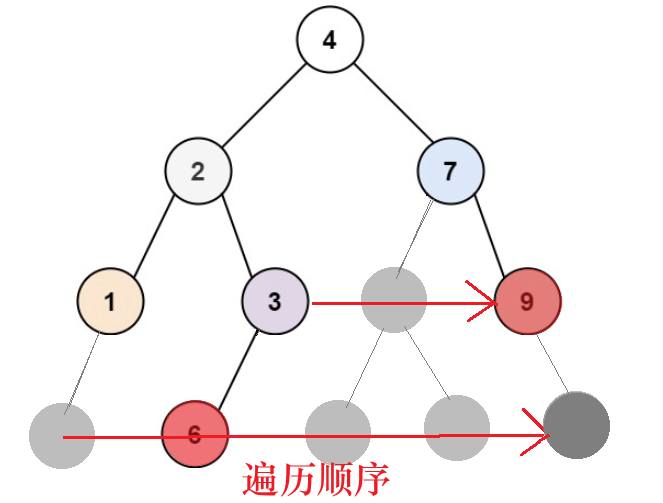
同样采用对列作为缓冲器。如果当我们出队列出到空时:对于完全二叉树而言,空结点后面应该全部都是空结点。如果有非空结点则为非完全二叉树。
4.2原理解释
4.2.1满二叉树的特点:
● 前n-1层全部都h是满结点。
● 第n层可能不是满结点,并且结点从左向右排列。
4.2.2判断规则
- 从根节点开始,逐层入队。
- 当遇到第一个
NULL节点时,后续所有出队的节点都必须是NULL。 - 如果在某个**
NULL** 之后又出现了非空节点,则说明存在"空缺",不是完全二叉树。
4.2.3结合以上------根本原理
- 我们用队列进行层序遍历,把每个节点的左右子节点依次入队(即使为空也入队一个
NULL)。 - 当第一次遇到
NULL时,表示某一层出现了空位。 - 此时若后面还有非空节点,意味着这个空位出现在中间位置,违背了"从左到右连续"的要求。
4.3代码呈现
cpp
bool BinaryTreeComplete(BTNode* root)
{
Queue p;
QueueInit(&p);
if (root)
{
QueuePush(&p, root);
}
while(!QueueEmpty(&p))
{
BTNode*ret=QueueFront(&p);
QueuePop(&p);
if (ret == NULL)
{
break;
}
}
while (!QueueEmpty)
{
BTNode* ret = QueueFront(&p);
QueuePop(&p);
if (ret == NULL)
{
QueueDestroy(&p);
return false;
}
}
QueueDestroy(&p);
return true;
}4.4流程讲解
初始化队列,将根节点入队
循环取出节点,直到遇到第一个 NULL
继续循环,检查剩余节点是否全为 NULL
若有非空 → 返回 false;否则返回 true
五,二叉树的销毁
二叉树的销毁是数据结构中一个经典且基础的操作,几乎在每一次算法面试中都会被考察。
cpp
void BinaryTreeDestory(BTNode* root)
{
if ((root)==NULL)
{
return;
}
BinaryTreeDestory((root)->_left);
BinaryTreeDestory((root)->_right);
free(root);
}5.1关键在于顺序控制
错误做法:先释放根节点,再释放子树 ------ 此时子树指针已失效,会导致段错误(Segmentation Fault)。
正确做法:必须先销毁左右子树,再销毁根节点。
这正是后序遍历(Left → Right → Root)的天然应用场景。
5.2为什么必须用后序遍历
- 如果我们提前释放
A,那么B和C的父指针就变成了野指针。 - 后续访问
B或C时,程序会崩溃。
| 语句 | 功能 |
|---|---|
if (root == NULL) return; |
边界条件:空树无需处理 |
BinaryTreeDestroy(root->_left); |
递归销毁左子树 |
BinaryTreeDestroy(root->_right); |
递归销毁右子树 |
free(root); |
释放当前节点内存 |
好了,本期文章就到这里,如果对你有帮助,还请一键三联支持,我是此方,我们下期再见