028动态规划之字符串DP——算法备赛

字符串DP

回文子串个数

问题描述

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

原题链接

思路分析

定义dp[i][j]表示子串[i,j]是否是一个回文串，它可以由dp[i+1,j-1]得到.

代码

int countSubstrings(string s) {
    int n=s.size();
    vector<vector<bool>>dp(n,vector<bool>(n));
    int ans=0;
    for(int j=0;j<n;j++){
        for(int i=0;i<=j;i++){  
            if(s[i]==s[j]&&(j-i<=2||dp[i+1][j-1])){  //dp[0,j-1][j-1]都计算过
                dp[i][j]=true;
                ans++;
            }
        }
    }
    return ans;
}

中心扩展法

代码

int countSubstrings(string s) {
    int n=s.size();
    int ans=0;
    for(int j=0;j<n;j++){
        int l=j,r=j;  //回文串为奇数时
        while(l>=0&&r<n&&s[l]==s[r]){
            ans++;
            l--;r++;
        }
        l=j,r=j+1;  //回文串为偶数时
        while(l>=0&&r<n&&s[l]==s[r]){
            ans++;
            l--;r++;
        }
    }
    return ans;
}

变成回文串的最少插入字符

蓝桥杯2016年省赛题

问题描述

给定一个字符串s，问最少在s中插入多少个字符，能使s变成回文串。

原题链接

思路分析

对于给定的字符串s，如果其已经是回文串了就是不用再插入了，直接输出0。

定义dp，dp[l][r]表示子串[l,r]最少需要插入的字符数，枚举l，r判断s[l]是否等于s[r]：

• 相等，dp[l][r]就等于dp[l+1][r-1]

• 不相等，那必须插入一个字符了，

  1. 要么 l 左边插入一个s[r],dp[l][r]=dp[l][r-1]+1
  2. 要么 r 右边插入一个s[l],dp[l][r]=dp[l+1][r]+1

  以上两种取最小值就是正确的dp[l][r]。

因为计算dp[l][r]要先计算dp[l+1][r]，dp[l][r-1]，dp[l+1][r-1]，可以采用dfs记忆化搜索较为直观地求解。

代码

#include <bits/stdc++.h>
using namespace std;
string str; 
vector<vector<int>>dp;
int dfs(int l,int r){
  if(l>=r) return 0;
  if(dp[l][r]!=-1) return dp[l][r];

  if(str[l]==str[r]){
    dp[l][r]=dfs(l+1,r-1);
  }else{
    dp[l][r]=min(dfs(l+1,r),dfs(l,r-1))+1;
  }
  return dp[l][r]; 
}
int main()
{
  // 请在此输入您的代码
  cin>>str;
  int n=str.size();
  dp=vector<vector<int>>(n,vector<int>(n,-1));
  cout<<dfs(0,n-1);  //记忆化搜索
  return 0;
}

最大回文子串

问题描述

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

原题链接

Manacher 算法

思路

首先只考虑字符串为奇数的字符串，后续再处理偶数字符串。

定义一个新概念臂长，表示中心扩展算法向外扩展的长度。如果一个位置的最大回文字符串长度为 2 * length + 1 ，其臂长为 length

定义i，i从0遍历到s.size()-1;定义一个j，j为遍历过程中 j 的右臂达到最大右边界（记为right）。

当在位置 i 开始进行中心拓展时，我们可以先找到 i 关于 j 的对称点 2 * j - i （ j-( i - j ) ）。那么如果点 2 * j - i 的臂长等于 n，我们就可以知道，点 i 的臂长至少为 min(j + length - i, n) （优化的关键点）。那么我们就可以直接 跳过 i 到 i + min(j + length - i, n) 这部分，从 i + min(j + length - i, n) + 1 开始拓展。

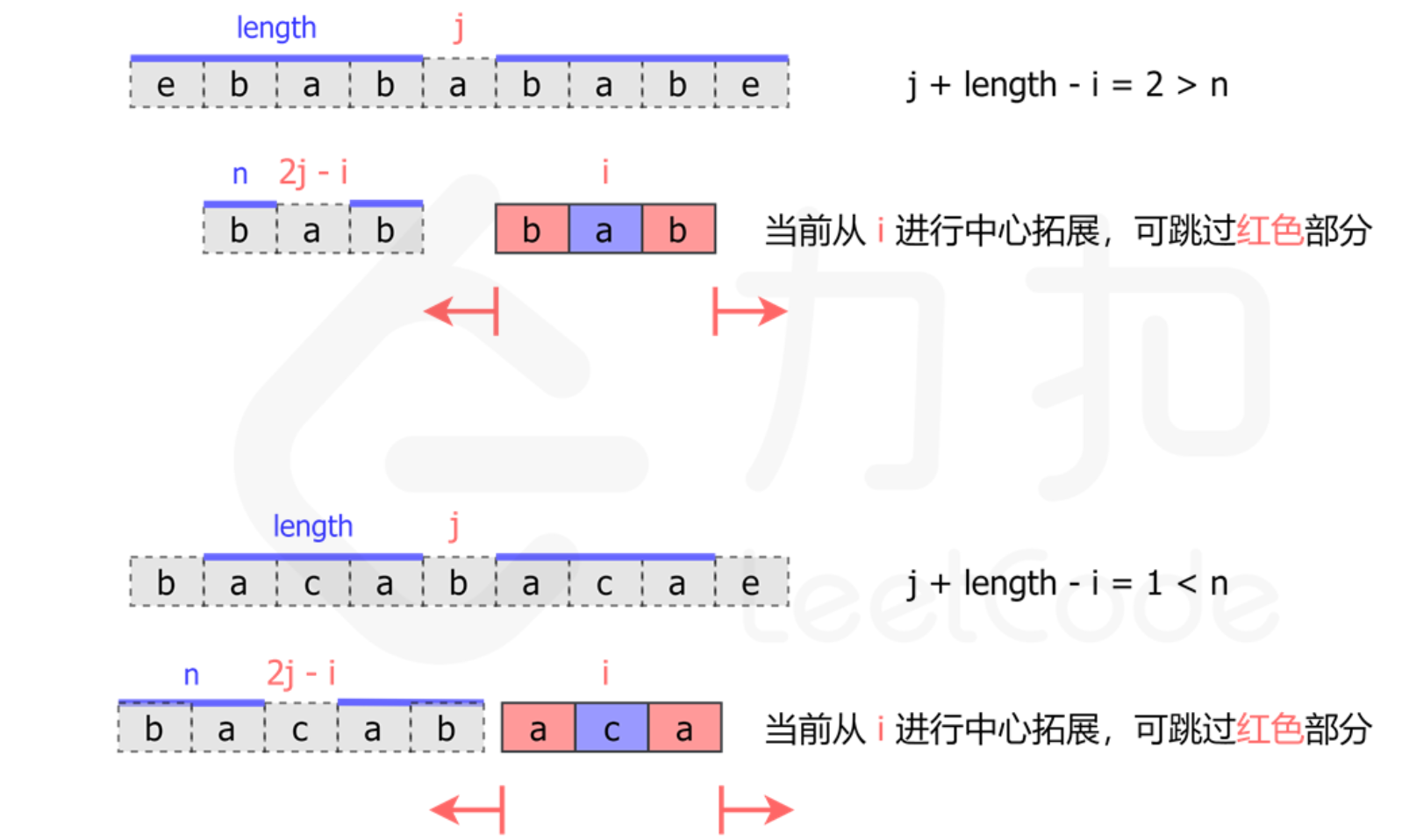
如何处理长度为偶数的回文字符串呢？

我们可以通过一个特别的操作将奇偶数的情况统一起来：我们向字符串的头尾以及每两个字符中间添加一个特殊字符 #，比如字符串 aaba 处理后会变成 #a#a#b#a#。

那么原先长度为偶数的回文字符串 aa 会变成长度为奇数的回文字符串 #a#a#，而长度为奇数的回文字符串 aba 会变成长度仍然为奇数的回文字符串 #a#b#a#，我们就不需要再考虑长度为偶数的回文字符串了。

在最后记录最终结果是时在去掉"#"即可

代码

int expand(const string& s, int left, int right) {  //求[left,right]的中心点的臂长
        while (left >= 0 && right < s.size() && s[left] == s[right]) {
            --left;
            ++right;
        }
        return (right - left - 2) / 2;  //此时的right，left比所求值多扩展了一步，所以要-2
    }

    string longestPalindrome(string s) {
        int start = 0, end = -1;
        string t = "#";
        for (char c: s) {
            t += c;
            t += '#';
        }
        t += '#';
        s = t;

        vector<int> arm_len;
        int right = -1, j = -1;  //定义初始值为-1，可省去起始时的分情况讨论
        for (int i = 0; i < s.size(); ++i) {
            int cur_arm_len;  //臂长
            if (right >= i) {  //i在右边界内，或可利用之前求得的记录求解
                int i_sym = j * 2 - i;  //寻找i关于j对称的点  j-(i-j)
                int min_arm_len = min(arm_len[i_sym], right - i); //点i的最少臂长
                cur_arm_len = expand(s, i - min_arm_len, i + min_arm_len);  //核心
            } else {  //i不在右边界内，直接求臂长
                cur_arm_len = expand(s, i, i);
            }
            arm_len.push_back(cur_arm_len);  //臂长记录
            if (i + cur_arm_len > right) {
                j = i;  //更新最大右边界的中心点
                right = i + cur_arm_len;  //记录右边界
            }
            if (cur_arm_len * 2 + 1 > end - start) {  //更新历史最大值
                start = i - cur_arm_len;  //更新目标的左边界
                end = i + cur_arm_len;  //更新目标的右边界
            }
        }
        string ans;
        for (int i = start; i <= end; ++i) {
            if (s[i] != '#') {
                ans += s[i];
            }
        }
        return ans;
    }

编辑距离

问题描述

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

原题链接

思路分析

定义dp[n+1][m+1]，dp[i][j]表示将word1中前 i 个字符转换为word2中前 j 个字符所需的最小操作数。dp[n][m]就是答案

一般情况下dp[i][j]=min{dp[i-1][j],dp[i][j-1],dp[i][j-1]}+1

min中的三个数+1分别代表以下三种操作

1. dp[i-1][j]+1，在word1的前i-1个字符转换后，删除第i个字符
2. dp[i][j-1]+1，在word1的前 i 个字符转换后，再插入一个字符
3. dp[i-1][j-1]+1，在word1的前 i-1个字符转换后，替换第i个字符

特殊情况 word[i-1]==word[j-1] (也就是word第i个字符与word第j个字符相等时) dp[i][j]可以直接等于dp[i-1][j-1]

dp[i][j]=min{dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]}

代码将两种情况做了合并处理

代码

int minDistance(string word1, string word2) {
        int n=word1.size(),m=word2.size();
       vector<vector<int>>dp(n+1,vector<int>(m+1));
       for(int i=0;i<=n;i++) dp[i][0]=i;
       for(int i=0;i<=m;i++) dp[0][i]=i;
       for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            dp[i][j]=min(min(dp[i][j-1],dp[i-1][j]),dp[i-1][j-1])+1;
            if(word1[i-1]==word2[j-1])
                dp[i][j]=min(dp[i][j],dp[i-1][j-1]);
        }
       }
       return dp[n][m];
    }

接龙序列

原题链接

思路分析

求删除最少的个数，相当于求最长的接龙序列长度

问题便转换为求最长的接龙序列长度

定义dp[10] 其中dp[i]表示当前所有数组成的最后末尾数字为i的最长接龙序列长度，每次更新dp后同时更新历史最长接龙序列长度，最后更新后的结果就是答案。

#include <iostream>
#include <string>
using namespace std;

int dp[10]={0};  //dp[i]存储的是末位数字为i的最长接龙序列。

int main()
{
  // 请在此输入您的代码
  int n;
  cin>>n;
  string s;  //用字符串接收数据，方便求首尾数位数字。本题不关心具体s是什么数值，只关心首尾数字。
  int m=0;
  for(int i=0;i<n;++i){
    cin>>s;
    int x=s[0]-'0',y=s[s.size()-1]-'0';
    dp[y]=max(dp[x]+1,dp[y]);  //对于每个尾数为y的s，可选择接在尾数为x的s的后面，或者不接。取决于能否最大化。
    m=max(m,dp[y]);  //更新历史最值
  }
  cout<<n-m<<endl;
  return 0;
}

子2023

蓝桥杯2023年国赛题

问题描述

原题链接

代码

string nums;
  for(int i=1;i<=2023;i++){
    string t=to_string(i);
    for(int j=0;j<t.size();j++){
      if(t[j]=='0'||t[j]=='2'||t[j]=='3'){  //预处理数据源，将非0,2,3的数字都排除
          nums+=t[j];
      }
    }
  }
  int n=nums.size();
  vector<long long>dp(4);
  for(int i=0;i<n;i++){
   if(nums[i]=='2'){
     dp[0]++;  //'2'子序列的个数，逢'2' +1
     dp[2]+=dp[1];  //'202'子序列的个数，逢'2'+前面'20'的子序列的个数
   }
   else if(nums[i]=='0'){
     dp[1]+=dp[0];  //'20'子序列的个数，逢'0'+前面'2'的子序列个数
   }
   else dp[3]+=dp[2];  //'2023'子序列的个数，逢'3'+前面'202'的子序列的个数
  }
  cout<<dp[3]; 

对字符串进行删除操作的最多次数

问题描述

给你一个长度为 n 的字符串 source ，一个字符串 pattern 且它是 source 的 子序列 ，和一个 有序 整数数组 targetIndices ，整数数组中的元素是 [0, n - 1] 中 互不相同 的数字。

定义一次 操作 为删除 source 中下标为 idx 的一个字符，且需要满足：

• idx 是 targetIndices 中的一个元素。
• 删除字符后，pattern仍然是source的一个 子序列。

执行操作后 不会 改变字符在 source 中的下标位置。比方说，如果从 "acb" 中删除 'c' ，下标为 2 的字符仍然是 'b' 。

请你返回 最多 可以进行多少次删除操作。

子序列指的是在原字符串里删除若干个（也可以不删除）字符后，不改变顺序地连接剩余字符得到的字符串。

原题链接

思路分析

定义 f，f[i][j]表示P(j)为S(i)的子序列，所能删除的最大次数，P(j)表示pattern前j个字符组成的字符串，S(i)表示source前i个字符组成的字符串。

将f中元素初始都为INT_MIN，可使前面有j+1次source[i] == pattern[j]的情况， f[i][j+1] 才会为非负数 f[i + 1][j+1] = f[i][j+1] + is_del才有为正数（才有意义）

数组多一层，可免去i=0，j=0的特殊情况判断。

代码

    int maxRemovals(string source, string pattern, vector<int>& targetIndices) {
        unordered_set<int> st(targetIndices.begin(), targetIndices.end());
        int n = source.length(), m = pattern.length();
        vector<vector<int>> f(n + 1, vector<int>(m + 1, INT_MIN));
        f[0][0] = 0;
        for (int i = 0; i < n; i++) {
            int is_del = st.count(i);  //tergetIndices存在该下标
            f[i + 1][0] = f[i][0] + is_del;  
            for (int j = 0; j < min(i + 1, m); j++) {
                f[i + 1][j + 1] = f[i][j + 1] + is_del;//S[i]至少存在子序列P[j+1]，f[i][j + 1]才不是负数
                if (source[i] == pattern[j]) {  //等于的话，多一种选择。
                    f[i + 1][j + 1] = max(f[i + 1][j + 1], f[i][j]);
                }
            }
        }
        return f[n][m];
    }
//作者：灵茶山艾府

时间复杂度：O(mn)

空间复杂度：O(mn)

空间优化

由于targetIndices是有序的数组，可以用一个指针寻找大于等于i的元素，

由于f[i]只与f[i-1]有关，所以可以用一维数组自我滚动优化空间。

代码

int maxRemovals(string source, string pattern, vector<int>& targetIndices) {
        int m = pattern.length();
        vector<int> f(m + 1,INT_MIN);
        f[0] = 0;
        int k = 0;
        for (int i = 0; i < source.length(); i++) {
            if (k < targetIndices.size() && targetIndices[k] < i) {
                k++;
            }
            int is_del = k < targetIndices.size() && targetIndices[k] == i;
            for (int j = min(i, m - 1); j >= 0; j--) {
                f[j + 1] += is_del;
                if (source[i] == pattern[j]) {
                    f[j + 1] = max(f[j + 1], f[j]);
                }
            }
            f[0] += is_del;
        }
        return f[m];
    }
//作者：灵茶山艾府

时间复杂度：O(mn)

空间复杂度：O(m)