基于因子图与和积算法的MATLAB实现

基于因子图（Factor Graph）与和积算法（Sum-Product Algorithm）的MATLAB实现

一、算法架构设计

1. 因子图建模

因子图由变量节点（Variable Nodes）和因子节点（Factor Nodes）构成二部图：

变量节点 ：表示随机变量（如x1,x2x_1, x_2x1,x2）
因子节点 ：表示变量间的函数关系（如f(x1,x2)f(x_1,x_2)f(x1,x2)）

2. 和积算法流程

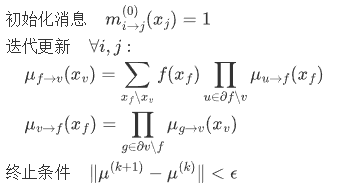
二、MATLAB核心实现

1. 数据结构定义

matlab 复制代码

% 因子图结构体
graph = struct(...
    'var_nodes', {{'x1', 'x2', 'x3'}}, ... % 变量节点
    'fac_nodes', {{@f1, @f2}}, ...        % 因子函数句柄
    'edges', {[1,2; 2,3]});              % 边连接关系

% 消息存储（对数域避免下溢）
log_messages = cell(length(graph.var_nodes), length(graph.fac_nodes));

2. 因子函数定义示例

matlab 复制代码

% 定义因子函数 f1(x1,x2) = exp(-0.5*(x1^2 + x2^2 + 2 * 0.3*x1*x2))
function f = f1(x1, x2)
    cov = [1, 0.3; 0.3, 1]; % 协方差矩阵
    f = mvnpdf([x1, x2], [0,0], cov);
end

% 定义因子函数 f2(x2,x3) = exp(-0.5*(x2^2 + x3^2))
function f = f2(x2, x3)
    cov = [1, 0; 0, 1];
    f = mvnpdf([x2, x3], [0,0], cov);
end

3. 消息传递算法实现

matlab 复制代码

function [log_beliefs, converged] = sum_product(graph, max_iter, epsilon)
    % 初始化消息
    num_vars = numel(graph.var_nodes);
    num_facs = numel(graph.fac_nodes);
    log_messages = cell(num_vars, num_facs);
    for i = 1:num_vars
        for j = 1:num_facs
            log_messages{i,j} = zeros(1, 2); % 假设变量为二元变量
        end
    end
    
    % 迭代更新
    converged = false;
    for iter = 1:max_iter
        log_messages_old = log_messages;
        
        % 因子→变量消息更新
        for f = 1:num_facs
            fac_node = graph.fac_nodes{f};
            connected_vars = find(graph.edges(:,f));
            for v = connected_vars
                % 计算边缘化消息
                product = 0;
                for u = connected_vars
                    if u ~= v
                        product = product + log_messages{u,f};
                    end
                end
                log_message = fac_node(connected_vars{v}) + product;
                log_messages{v,f} = log_message;
            end
        end
        
        % 变量→因子消息更新
        for v = 1:num_vars
            connected_facs = find(graph.edges(:,v));
            for f = connected_facs
                product = sum(log_messages{v,f});
                for u = connected_facs
                    if u ~= f
                        product = product + log_messages{v,u};
                    end
                end
                log_beliefs{v} = log_beliefs{v} + product;
            end
        end
        
        % 收敛判断
        if max(abs(log_messages(:) - log_messages_old(:))) < epsilon
            converged = true;
            break;
        end
    end
end

三、参考

参考代码
- 因子图和和积算法的matlab实现 youwenfan.com/contentcsm/52466.html
仿真案例
- LDPC编解码仿真 github.com/ldpcmatlab/ldpc-code
  基于和积算法的迭代译码实现