0010集成学习(Ensemble Learning)

老欧学视觉2025-12-02 13:14

0010集成学习Ensemble Learning

  • 一、集成学习介绍
  • 二、Bagging（并行集成）
    • [1.1 Bagging思想概述](#1.1 Bagging思想概述)
    • [2.2 代码实现Bagging思想](#2.2 代码实现Bagging思想)
      • [2.2.1 API查看](#2.2.1 API查看)
      • [2.2.2 代码演示Bagging思想](#2.2.2 代码演示Bagging思想)
    • [3.3 随机森林(Random Forest)](#3.3 随机森林(Random Forest))
  • 三、Boosting（串行集成）
    • [1.1 AdaBoost算法](#1.1 AdaBoost算法)
      • [1.1.1 AdaBoost算法原理](#1.1.1 AdaBoost算法原理)
      • [1.1.2 Adaboost算法的直观理解](#1.1.2 Adaboost算法的直观理解)
      • [1.1.3 Adaboost算法的python实现](#1.1.3 Adaboost算法的python实现)
    • [2.2 GBDT算法](#2.2 GBDT算法)
      • [2.2.1 GBDT算法原理](#2.2.1 GBDT算法原理)
      • [2.2.2 GBDT直观理解](#2.2.2 GBDT直观理解)
      • [2.2.3 GBDT算法思想的python实现](#2.2.3 GBDT算法思想的python实现)
    • [3.3 XGBoost算法](#3.3 XGBoost算法)
      • [1.1 算法理解](#1.1 算法理解)
      • [2.2 代码演示](#2.2 代码演示)
  • 四、Bagging、Boosting的区别
  • 五、Stacking思想
    • [1.1 stacking算法](#1.1 stacking算法)
    • [2.2 python代码实现](#2.2 python代码实现)

一、集成学习介绍

  • 集成学习是一种思想，不是算法。其核心是组合多个基础模型的预测结果，以提升整体性能的机器学习方法。将若干个弱学习器(分类器&回归器)组合之后产生一个新学习器。集成算法的成功在于保证弱分类器的多样性
  • 核心思想：
    • 单个模型（如决策树、逻辑回归）易存在偏差或方差问题，集成学习通过 "群体智慧" 弥补短板。
    • 核心逻辑是 "三个臭皮匠顶个诸葛亮"，让多个弱学习器（性能略优于随机猜测的模型）协同，形成强学习器。
  • 常见的集成学习类型：
    • Bagging（并行集成）：多个模型独立训练，结果通过投票或平均合并，代表算法是随机森林。
    • Boosting（串行集成）：模型依次训练，后一个模型专注修正前一个的错误，代表算法有 AdaBoost、XGBoost。
    • Stacking（堆叠集成）：用多个基础模型的输出作为新特征，训练一个元模型（如逻辑回归）做最终预测。

二、Bagging（并行集成）

1.1 Bagging思想概述

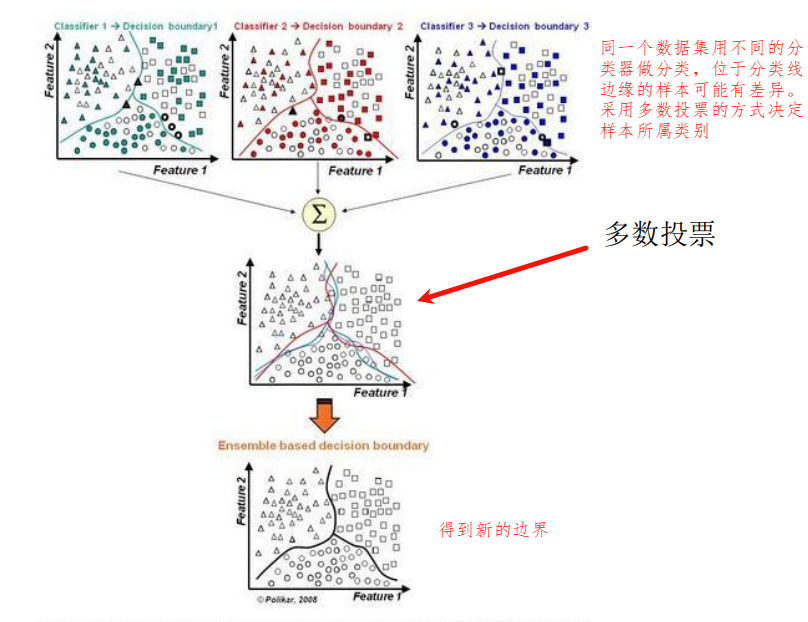
  • Bagging方法又叫做自举汇聚法(Bootstrap Aggregating)，它的思想是：在原始数据集上通过有放回的抽样(bootstrap)的方式，重新选择出S个新数据集来分别训练S个分类器/回归器的集成技术。
    • 有放回的抽样(bootstrap)，举例说明：比如有10个样本，每次抽取1个，重新放回去，连续抽取10次，得到10条样本
  • Bagging方法的弱学习器（基学习器）可以是基本的算法模型，eg: Linear、Ridge(L2惩罚）、Lasso（L1惩罚）、Logistic、Softmax、ID3、C4.5、CART（C表示分类树，A表示回归树）、SVM（SVC和SVR）、KNN等。
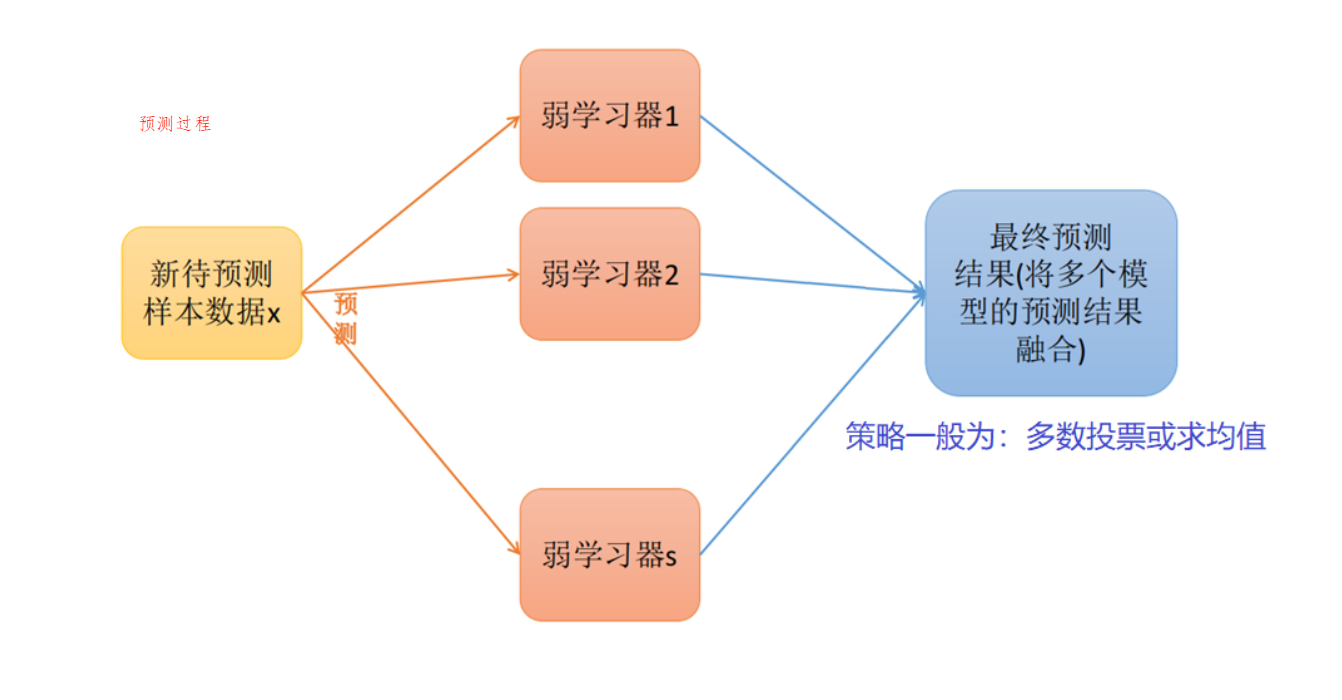
  • Bagging方法训练出来的模型在预测新样本分类/回归的时候，会使用多数投票或者求均值的方式来统计最终的分类/回归结果。
  • Bagging方式是有放回的抽样，并且每个子集的样本数量必须和原始样本数量一致，所以抽取出来的子集中是存在重复数据的，模型训练的时候允许存在重复数据。

2.2 代码实现Bagging思想

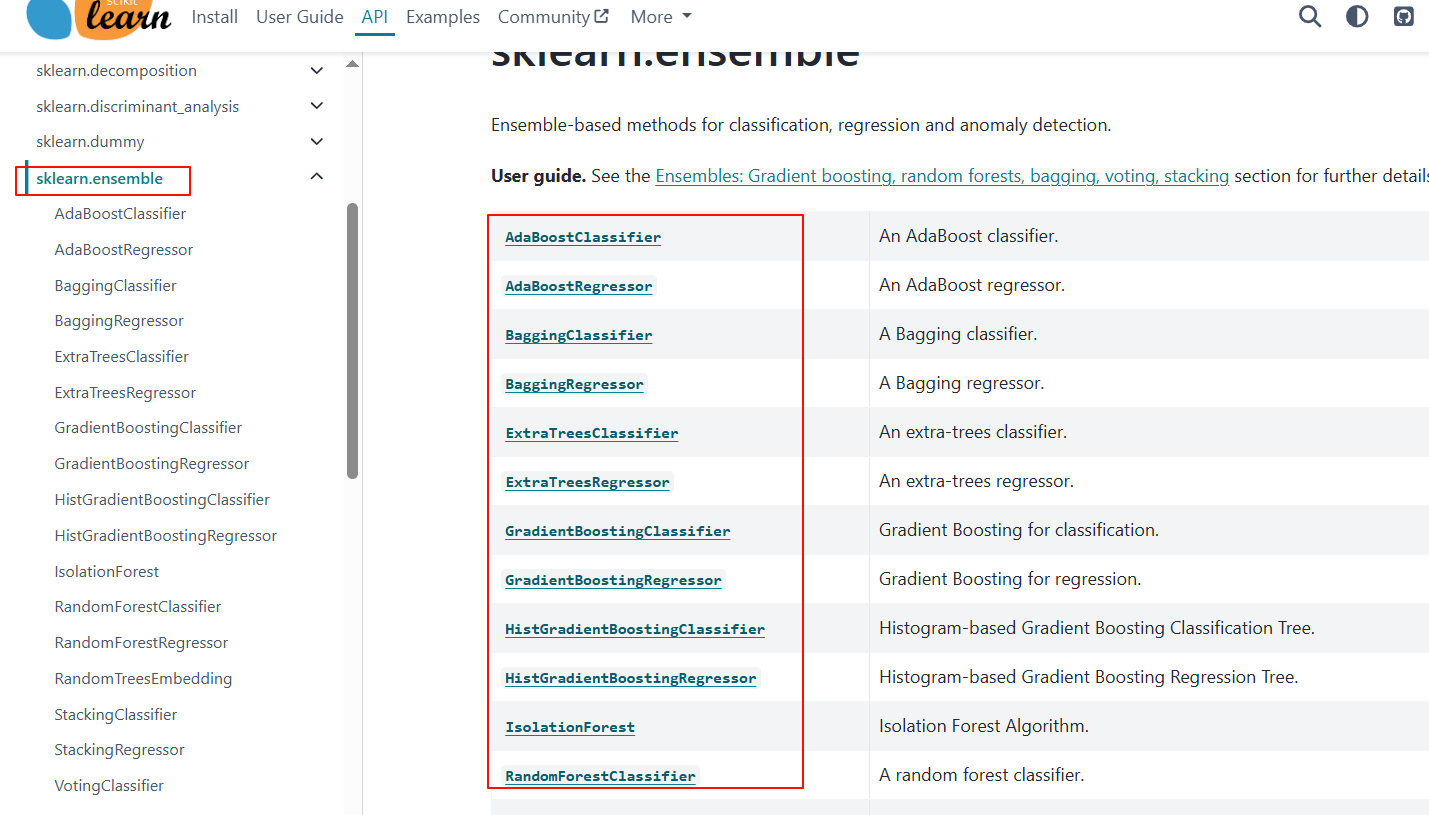
2.2.1 API查看

网址：https://scikit-learn.org/stable/api/sklearn.ensemble.html

2.2.2 代码演示Bagging思想

python 复制代码 
import sys

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor  # 决策树回归器（可通过max_depth控制树深度）
from sklearn.metrics import r2_score  # 用于计算R²决定系数（评估回归模型性能）

'''
bagging 回归
核心思想：通过有放回抽样（bootstrap）生成多个不同的训练集，
每个训练集训练一个弱学习器（此处为深度为1的决策树，即决策树桩），
最终预测结果通过多个弱学习器的预测值取平均得到，降低模型方差，提升稳定性
'''
# 构建示例数据集：包含10个样本，特征X为1-10的整数，目标变量Y为对应响应值
df = pd.DataFrame([[1, 10.56],
                   [2, 27],
                   [3, 39.1],
                   [4, 40.4],
                   [5, 58],
                   [6, 60.5],
                   [7, 79],
                   [8, 87],
                   [9, 90],
                   [10, 95]],
                  columns=['X', 'Y'])  # 定义列名，X为特征列，Y为目标列
# print(df)  # 可选：打印数据集查看数据结构

M = []  # 初始化列表，用于存储训练好的所有弱学习器
n_trees = 200  # 设定要构造的弱学习器（决策树桩）数量

# 循环训练n_trees个弱学习器，核心是bootstrap抽样（有放回抽样）
for i in range(n_trees):
    '''
    DataFrame.sample() 抽样方法参数说明：
    frac=1.0: 抽样比例为100%（即抽样后样本数量与原数据一致）
    replace=True: 允许有放回抽样（bootstrap核心，确保不同训练集存在差异）
    不设置random_state：每次运行抽样结果不同，增强模型随机性
    '''
    tmp = df.sample(frac=1.0, replace=True)  # 对原数据进行有放回抽样，生成临时训练集
    # tmp = tmp.drop_duplicates()  # 可选：去除重复样本（此处注释未启用）
    X = tmp.iloc[:, :-1]  # 提取临时训练集的特征（所有行，除最后一列外）
    Y = tmp.iloc[:, -1]  # 提取临时训练集的目标变量（所有行，最后一列）

    model = DecisionTreeRegressor(max_depth=1)  # 初始化弱学习器：深度为1的决策树（决策树桩）
    model.fit(X, Y)  # 用临时训练集训练弱学习器

    M.append(model)  # 将训练好的弱学习器存入列表M

### 模型预测与性能评估
x = df.iloc[:, :-1]  # 提取全部数据的特征（用于预测）
y = df.iloc[:, -1]  # 提取全部数据的真实目标值（用于评估）

# 1. 单棵决策树桩的性能评估（作为对比基准）
mode01 = DecisionTreeRegressor(max_depth=1)  # 初始化单棵决策树桩
mode01.fit(x, y)  # 用全部数据训练单棵决策树桩
y_hat_01 = mode01.predict(x)  # 单棵树的预测结果
print(y_hat_01)  # 打印单棵树的预测值
print(mode01.score(x, y))  # 打印单棵树的R²分数（sklearn内置评分方法）
print('R2:', r2_score(y, y_hat_01))  # 用r2_score函数计算R²（与上一行结果一致）
print("-" * 100)  # 分隔线，区分单棵树与bagging模型结果

# 2. Bagging集成模型的预测与评估
res = np.zeros(df.shape[0])  # 初始化预测结果数组（长度=样本数量，初始值为0）
for j in M:  # 遍历所有训练好的弱学习器
    res += j.predict(x)  # 累加每个弱学习器的预测值
y_hat = res / n_trees  # 取所有弱学习器预测值的平均值（bagging集成核心）

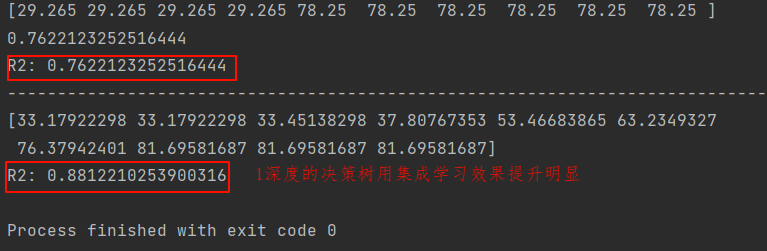
print(y_hat)  # 打印bagging集成模型的预测值
print('R2:', r2_score(y, y_hat))  # 计算并打印bagging模型的R²分数（对比单棵树，通常更高）

运行结果：

3.3 随机森林(Random Forest)

随机森林是在Bagging策略的基础上进行修改后的一种算法

  • 从原始样本集(n个样本)中用Bootstrap采样(有放回重采样)选出n个样本；
  • 使用抽取出来的子数据集(存在重复数据)来训练决策树；从所有属性中随机选择K个属性，属性就是特征的意思，从所有特征里面随机找K个特征，构建特征数据的多样性，从K个属性中选择出最佳分割属性作为当前节点的划分属性，按照这种方式来迭代的创建决策树；
  • 重复以上两步m次，即建立m棵决策树；
  • 这m个决策树形成随机森林，通过投票表决结果决定数据属于那一类(分类任务)；通过求平均值得到最终的预测值(回归任务)。
  • 随机森林的基学习器一定是决策树。 Bagging不一定是决策树。

3.3.1scikit-learn相关参数

3.3.2 代码演示随机森林

数据集见资源绑定

重点理解：pca降维、管道Pipeline、网格调参

python 复制代码 
import pandas as pd
import numpy as np
import sys
# from sklearn.preprocessing import Imputer
from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, MinMaxScaler  ##标准化，归一化
from sklearn.decomposition import PCA
from sklearn.model_selection import GridSearchCV

pd.set_option("display.max_columns", None)

##读取数据
data = pd.read_csv('data/risk_factors_cervical_cancer.csv', sep=',')
# print(data.head())
# print(data.info())
names = data.columns
# print(names)
# sys.exit()
##数据清洗
data.replace('?', np.nan, inplace=True) # 替换？为NAN（not a number不是一个数据）
###使用Imputer进行缺省值的填充 列填充
# imputer = Imputer(missing_values='NaN', strategy='mean', axis=0)
imputer = SimpleImputer()  # 按列取均值，均值填充
data = imputer.fit_transform(data)
data = pd.DataFrame(data, columns=names) # 重新转成dataframe
# print(data.head())
# print(data.info())
# sys.exit()
###获取特征属性X 和目标属性Y
X = data.iloc[:, :-4]  # 最后4列都是标签
Y = data.iloc[:, -4:].astype('int') # 标签要转int
# print(X.info())
# print(Y.info())
# sys.exit()
# 数据分割
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=10)

# 构建一个管道Pipeline ，表示流水线工作先做pca再做RF
# 数据标准化，数据归一化 （数据量纲） 决策树来说我们其实不需要做这个操作
# 标准化：把数据转化为均值为0，方差为1的
# 归一化：把数据压缩到0-1

# PCA降维
models = [Pipeline([('standarscaler', StandardScaler()),  # StandardScaler() 归一化，决策树不用归一化，特征之间没有联系
                    ('pca', PCA()),
                    ('RF', RandomForestClassifier())]),
          Pipeline([
              ('pca', PCA(n_components=0.5)),  # 数据有大量0，要做pca降维，比如40个0，降维后剩余40-0.5=20个
              ('RF', RandomForestClassifier(n_estimators=10, max_depth=20))])  # 10课树，20深度
          ]

###设置参数
params = {'pca__n_components': [0.5, 0.6, 0.7, 0.8, 0.9],
          'RF__n_estimators': [50, 100, 150],
          'RF__max_depth': [1, 3, 5, 7]}
##网格调参
model = GridSearchCV(estimator=models[1], param_grid=params, cv=5)  # cv=5 5则交叉验证
##训练
model.fit(x_train, y_train)
print('最优参数：', model.best_params_)
print('最优模型：', model.best_estimator_)
print('最优模型的分数：', model.best_score_)
print(model.score(x_train, y_train))  # 训练集打分
print(model.score(x_test, y_test))  # 测试集打分

# model = models[1]
# model.fit(x_train, y_train)
# print(model.score(x_train, y_train))
# print(model.score(x_test, y_test))

# ###保存模型
# from sklearn.externals import joblib
# import joblib
# joblib.dump(model,'./model/risk01.m')

三、Boosting（串行集成）

在随机森林的构建过程中，各棵树之间是没有关系的，相对独立的；

在构建的过程中，构建第m棵子树的时候，不会考虑前面的m-1棵树。而Boosting则弥补了这种缺陷。

  • 提升学习（Boosting）是一种机器学习技术，可以用于回归和分类的问题，它每一步产生 弱预测模型(如决策树)，并加权累加到总模型中。
  • 提升技术的意义：如果一个问题存在弱预测模型，那么可以通过提升技术的办法得到一个 强预测模型。
  • 常见的模型有：
    • Adaboost
    • Gradient Boosting(GBT/GBDT/GBRT)

1.1 AdaBoost算法

  • Adaptive Boosting是一种迭代算法。每轮迭代中会在训练集上产生一个新的学习器，然后使用该学习器对所有训练样本进行预测，以评估每个样本的重要性(Informative)。换句话来讲就是，算法/子模型会为每个样本赋予一个权重，每次用训练好的学习器标注/预测各个样本(训练数据)，如果某个样 本点被预测的越正确，则将样本权重降低；否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的权重就越大，也就是说越难区分的样本在 训练过程中会变得越重要；
  • 整个迭代过程直到错误率足够小或者达到一定的迭代次数为止。

1.1.1 AdaBoost算法原理









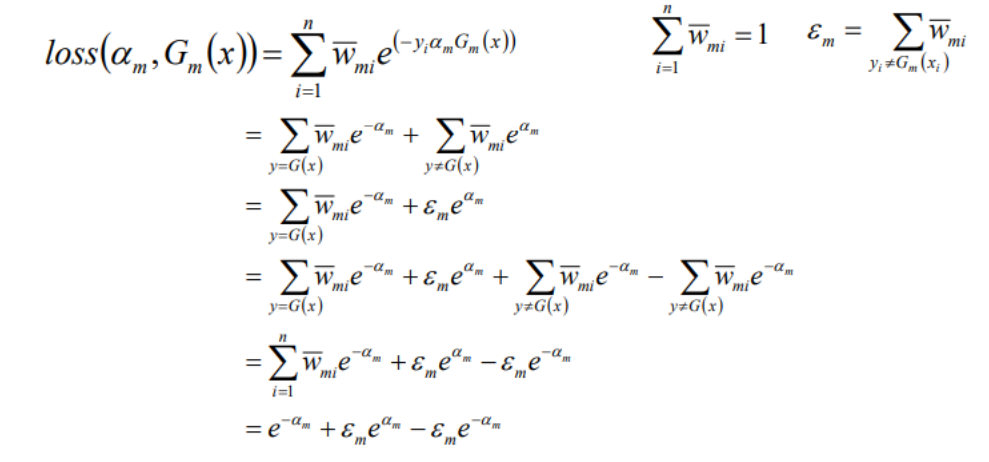
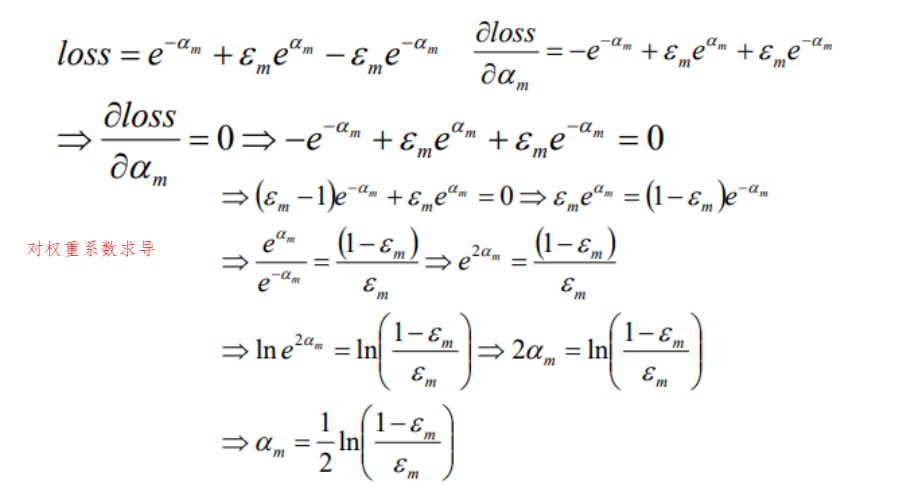
实现过程汇总：

1.1.2 Adaboost算法的直观理解










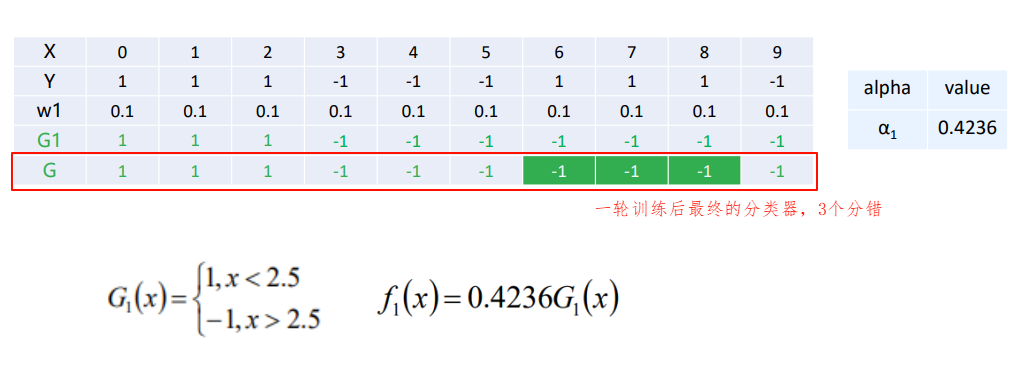
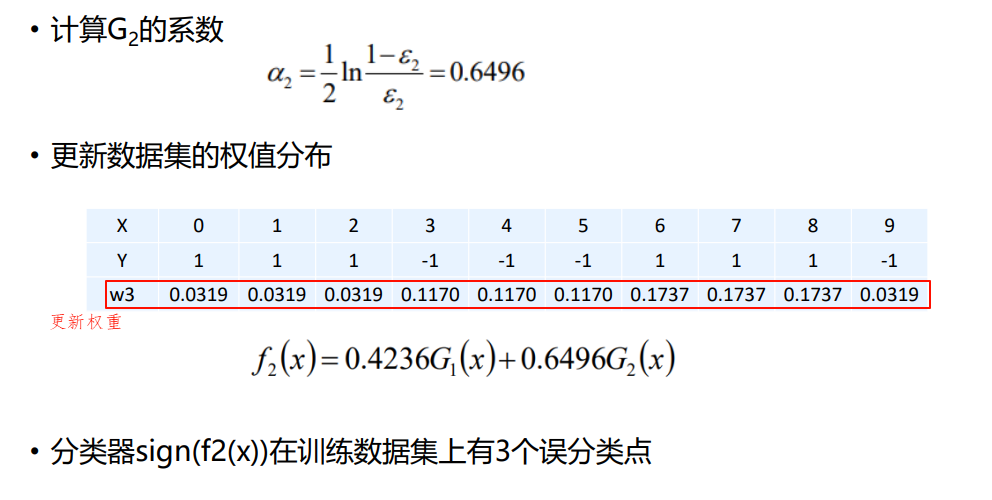
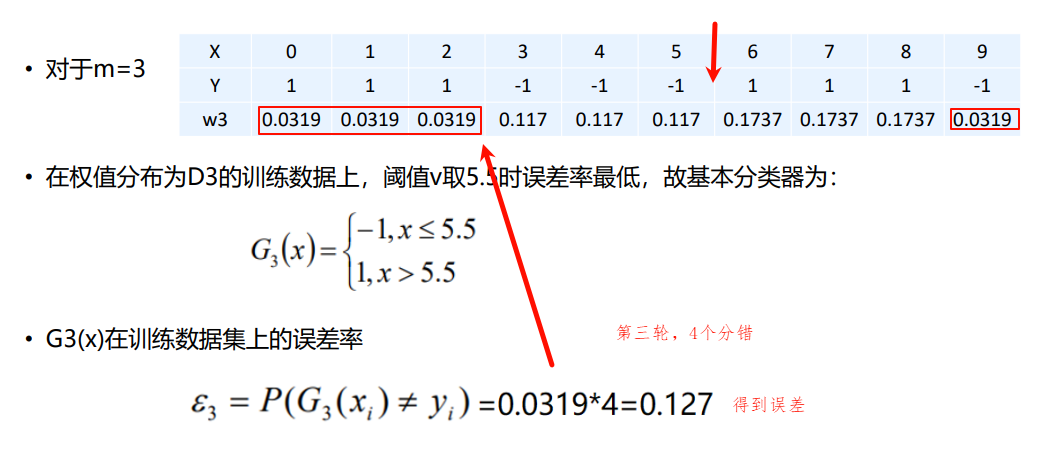
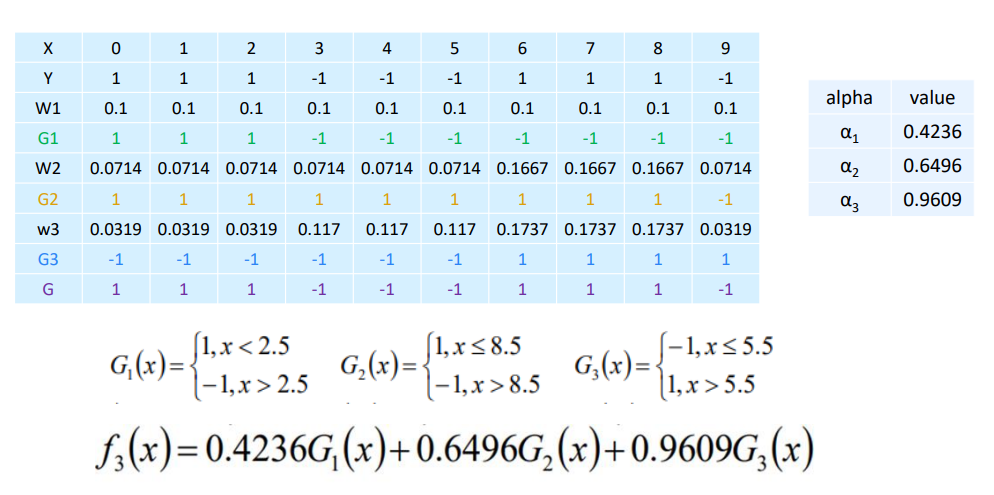
1.1.3 Adaboost算法的python实现

python 复制代码 
import sys
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import f1_score, accuracy_score
# 这种情况下用一个弱分类器去划分，划分不对
df = pd.DataFrame([[0, 1],
                   [1, 1],
                   [2, 1],
                   [3, -1],
                   [4, -1],
                   [5, -1],
                   [6, 1],
                   [7, 1],
                   [8, 1],
                   [9, -1]])
X = df.iloc[:, :-1]
Y = df.iloc[:, -1]

# 第一个弱学习器
# 1、初始化样本权重 第一步：等权重
w0 = np.ones(df.shape[0]) / df.shape[0]
# print(w0)
# sys.exit()
# 2、构造弱分类器G1
model1 = DecisionTreeClassifier(max_depth=1)  # 初始化深度为1的若分类器
model1.fit(X, Y, sample_weight=w0)  # 带着权重去fit训练
# print(model1.predict(X)) # 查看分类情况
# print(model1.predict(X)!=Y)
# print(w1[model1.predict(X)!=Y])
# 3、计算第一次预测完后的误差率
e1 = sum(w0[model1.predict(X) != Y])
# print(e1)
# sys.exit()
# 4、弱学习器G1的权重α1
a1 = 0.5 * np.log((1 - e1) / e1)
# print("a1 =", a1)
# sys.exit()
# 5、第一轮后的强学习器 f = a1*G1
# y_hat = np.sign(a1 * model1.predict(X))
# print(Y.tolist())  # 真实值
# print(y_hat)  # 预测值
# sys.exit()
print("-" * 50)

# 第二个弱学习器G2
# 6、更新样本权重值
w1 = w0 * np.exp(-a1 * Y * model1.predict(X))
# print(w2)
w1 = np.array(w1 / sum(w1))  # 归一化
# print(w1)
# sys.exit()
# 7、训练模型G2
model2 = DecisionTreeClassifier(max_depth=1)
model2.fit(X, Y, sample_weight=w1)
# print(model2.predict(X))
# print(model2.predict(X)!=Y)
# print(w2[model2.predict(X)!=Y])
# 8、误差率e2
e2 = sum(w1[model2.predict(X) != Y])
# print(e2)
# sys.exit()
# 9、求G2的权重α2
a2 = 0.5 * np.log((1 - e2) / e2)
# print("a2 =", a2)
# sys.exit()
# 10、强学习器f = a1*G1+a2*G2
y_hat = np.sign(a1 * model1.predict(X) + a2 * model2.predict(X))
y_hat2 = np.sign(model2.predict(X))
# print(Y.tolist())
# print(y_hat)
# print(y_hat2)
# sys.exit()
# print("*" * 50)
# 第三个弱学习器 G3
# 11、更新样本权重值
# 以下两种写法都是正确的，虽然得到的w2值不同(因为后者没有考虑w0)，但是归一化之后的结果是一致的。
w2 = w1 * np.exp(-Y * a2 * model2.predict(X))
w2 = np.exp(-Y * a1 * model1.predict(X) - Y * a2 * model2.predict(X))
# print(w2)
w2 = np.array(w2 / sum(w2))  #归一化
# print("w2 =", w2)
# sys.exit()
# 12 、训练模型G3
model3 = DecisionTreeClassifier(max_depth=1)
model3.fit(X, Y, sample_weight=w2)
# print(model3.predict(X))
# sys.exit()
# 13、误差率e3
e3 = sum(w2[model3.predict(X) != Y])
# print(e3)
# 14、求G3的权重α3
a3 = 0.5 * np.log((1 - e3) / e3)
# print("a3=", a3)
# sys.exit()
# 预测
# 强学习器f = a1*G1+a2*G2+a3*G3
y_hat = np.sign(a1 * model1.predict(X) + a2 * model2.predict(X) + a3 * model3.predict(X))
y_hat3 = np.sign(model3.predict(X))
print(Y.tolist())
print(y_hat)
print(y_hat3)

print(a1 * model1.predict(X))
print(a2 * model2.predict(X))
print(a3 * model3.predict(X))

把以上代码整理成一个方法或者一个类，循环的方式；最大迭代次数、停止条件的误差率、决策树的超参、底数【2，e】

2.2 GBDT算法

GBDT也是Boosting算法的一种，GBDT和AdaBoost都是加法模型，二者的区别如下：

  1. AdaBoost算法根据前一轮的弱学习器的误差来更新样本权重值，然后进行迭代；GBDT算法根据前一轮的弱学习器的误差来重新计算目标值，然后进行迭代。
  2. AdaBoost算法主要用于解决分类问题，它的基学习器是CART分类树，但AdaBoost也可以进行回归任务的处理，这种变体被称为AdaBoost.R2，它使用CART回归树作为基学习器。而GBDT算法既可以用于解决分类问题，也可以用于解决回归问题，无论用于解决分类问题还是回归问题，
    GBDT算法的底层都是CART回归树。

GBDT的别名：GBT(Gradient Boosting Tree)、GTB(Gradient Tree Boosting)

GBRT(Gradient Boosting Regression Tree)GBDT(Gradient Boosting Decison Tree)、MART(Multiple Additive Regression Tree)

2.2.1 GBDT算法原理



• GBDT回归算法和分类算法的唯一区别是：选择的损失函数不同，因而对应的负梯度值不同，采用的模型初值也不一样。

• 回归算法选择的损失函数一般是均方差(最小二乘)和绝对值误差， 分类算法中一般选择对

数损失函数来表示。


2.2.2 GBDT直观理解


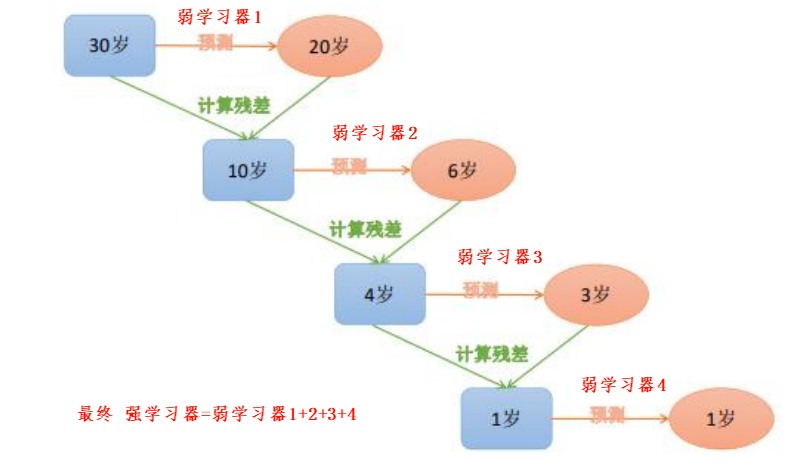
2.2.3 GBDT算法思想的python实现

python 复制代码 
import sys
import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
# 数据
df = pd.DataFrame([[1, 5.56],
                   [2, 5.7],
                   [3, 5.91],
                   [4, 6.4],
                   [5, 6.8],
                   [6, 7.05],
                   [7, 8.9],
                   [8, 8.7],
                   [9, 9],
                   [10, 9.05]],
    columns=['X', 'Y'])
# df = pd.read_csv('./data/boston_housing.data', sep='\s+', header=None)
X = df.iloc[:, :-1]
Y = df.iloc[:, -1]
y = Y  # 保留原始的Y

# Fm = F0+v*f1+v*f2+v*f3+...v*fm

# 1、第一个弱学习器F0，demo是个回归问题
F0 = np.mean(Y)
# F0 = ln(odds)
M = [F0]  # M是最终的强学习器，现在有一个元素
# f1第一棵树 标签（label） Y-F0
Y = Y - F0  # 残差作为梯度，回归（平方和损失）--》得到新的Y
n_trees = 10  # 训练10棵树
learning_rate = 0.6  # 学习率
for i in range(n_trees):
    model = DecisionTreeRegressor(max_depth=1)  # 深度为1的树
    model.fit(X, Y)  # 训练
    Y = Y - learning_rate * model.predict(X)  # 每训练一次更新残差
    M.append(model)  #
# print(M)
# sys.exit()
# 预测
res = np.zeros(df.shape[0])
for j in range(len(M)):
    if j == 0:
        res += M[j]
        # print(res)
    else:
        res += learning_rate * M[j].predict(X)
        # print(res)
print(y)
print(res)
y_hat = res
print(r2_score(y, y_hat))

3.3 XGBoost算法

1.1 算法理解

  • XGBoost是GBDT（Gradient Boosting Decision Tree）梯度提升树的一个改进版 本。

    XGBoost能够更快的、更高效率的训练模型，XGBoost中的X代表的就是 eXtreme（极致）

  • 按照XGBoost发明人陈天奇的介绍： XGBoost是一个可拓展的Tree boosting算法， 被广泛用于数据科学领域

  • GBoost曾经是Kaggle竞赛的传奇------在2015年的時候29个Kaggle冠军队伍中有17队在他们的解决方案中使用了XGboost。人们越来越意识到XGBoost的强大 威力。

  • 官网地址：http://xgboost.readthedocs.io

  • Github源码地址：https://github.com/dmlc/xgboost

  • XGBoost支持开发语言:Python、R、Java、Scala、C++等

  • XGboost的基本组成元素是：决策树；我们将这些决策树称为"弱学习器 "，这些"弱学习器"共同组成了XGboost

  • 组成XGBoost的决策树之间是有先后顺序的；后一棵决策树的生成会考虑 前一棵决策树的预测结果，即将前一棵决策树的偏差考虑在内（在目标函数中有体现）

  • 生成每棵决策树使用的数据集，是整个数据集。所以可以将每棵决策树的生成都看作是一个完整的决策树生成过程





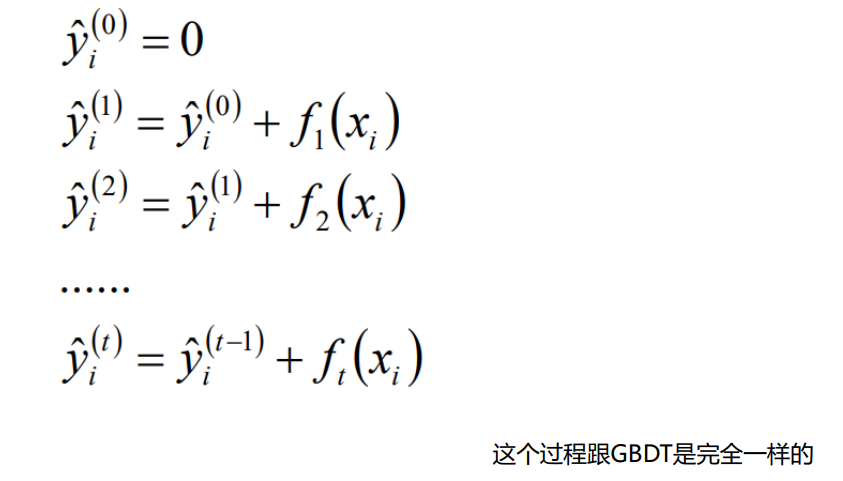
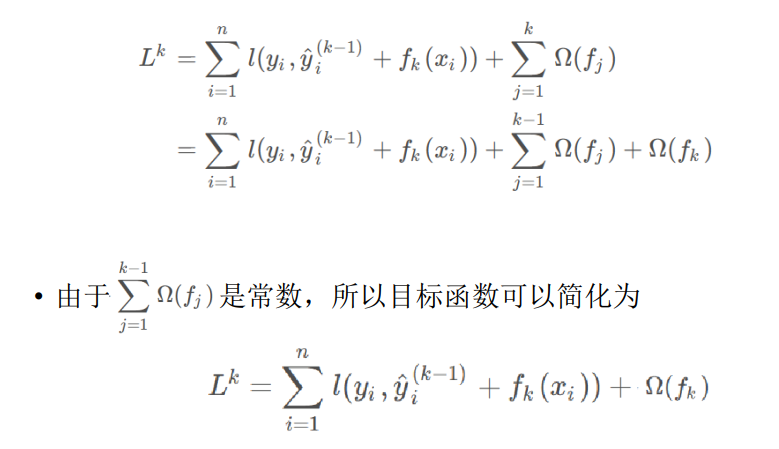
2.2 代码演示

1、环境安装

pip install xgboost -i https://pypi.tuna.tsinghua.edu.cn/simple/

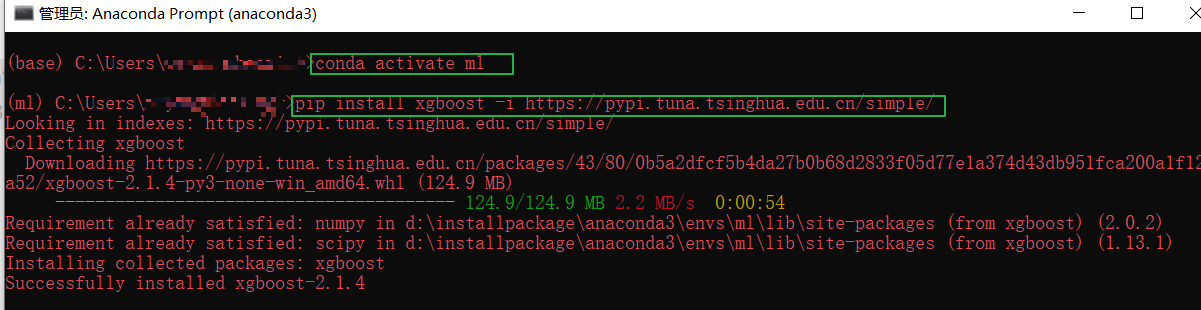
2、XGBoost回归代码示例

python 复制代码 
import xgboost as xgb
from xgboost import plot_importance
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
import pandas as pd

# 导入数据集
data = pd.read_csv('./data/boston_housing.data', sep='\s+', header=None)

# 获取特征属性X和目标属性Y
X = data.iloc[:, :-1]
y = data.iloc[:, -1]

# Xgboost训练过程
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=10)

model = xgb.XGBRegressor(max_depth=5, learning_rate=0.1, n_estimators=160, objective='reg:gamma')
# model = xgb.XGBRegressor(max_depth=5, learning_rate=0.2, n_estimators=100, objective='reg:squarederror')
model.fit(X_train, y_train)


print("训练集上的R^2 = {:.3f} ".format(r2_score(y_train, model.predict(X_train))))
print("测试集上的R^2 = {:.3f} ".format(r2_score(y_test, model.predict(X_test))))

# 绘制出特征重要性的图表，用于帮助我们了解哪些特征对于模型的预测效果影响较大，从而进行特征选择和优化。
plot_importance(model)
plt.show()

3、XGBoost分类代码示例

python 复制代码 
from sklearn.datasets import load_iris
import xgboost as xgb
from xgboost import plot_importance
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import f1_score

# read in the iris data
iris = load_iris()

X = iris.data
y = iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=10)

# 训练模型
model = xgb.XGBClassifier(max_depth=5, learning_rate=0.1, n_estimators=160, objective='multi:softmax')
model.fit(X_train, y_train)

# 对测试集进行预测
ans = model.predict(X_test)

# 计算准确率
cnt1 = 0
cnt2 = 0
for i in range(len(y_test)):
    if ans[i] == y_test[i]:
        cnt1 += 1
    else:
        cnt2 += 1

print("Accuracy: %.2f %% " % (100 * cnt1 / (cnt1 + cnt2)))

score = f1_score(y_test, ans, average='micro')
print("F1 score: %.2f %% " % score)

# 绘制出特征重要性的图表，用于帮助我们了解哪些特征对于模型的预测效果影响较大，从而进行特征选择和优化。
plot_importance(model)
plt.show()

四、Bagging、Boosting的区别

  • 样本选择：Bagging算法是有放回的随机采样；Boosting算法是每一轮训练集不变，只是训练集中的每个样本在分类器中的权重发生变化或者目标属性y发生变化，而权重&y值都是根据上一轮的预测结果进行调整；
  • 样本权重：Bagging使用随机抽样，样本是等权重；Boosting根据样本被分类错误与否不断的调整样本的权重值，分类错误的样本权重大(Adaboost)；
  • 预测函数：Bagging所有预测模型的权重相等；Boosting算法对于误差小的分类器具有更大的权重（Adaboost）；
  • 并行计算：Bagging算法可以并行生成各个基模型；Boosting理论上只能顺序生产，因为后一个模型需要前一个模型的结果；
  • Bagging是减少模型的variance(方差)；Boosting是减少模型的Bias(偏度)。

五、Stacking思想

1.1 stacking算法

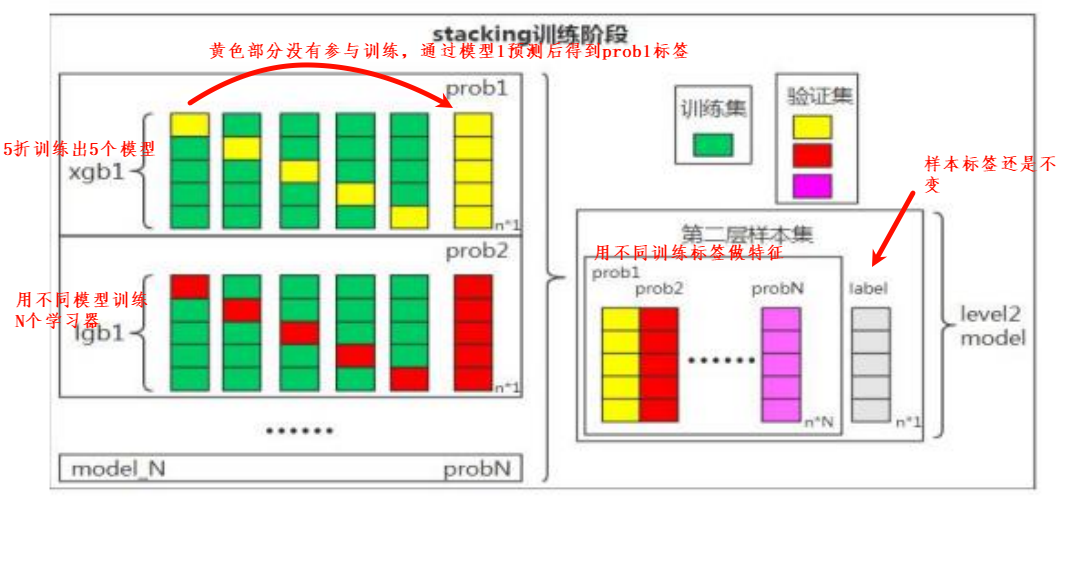
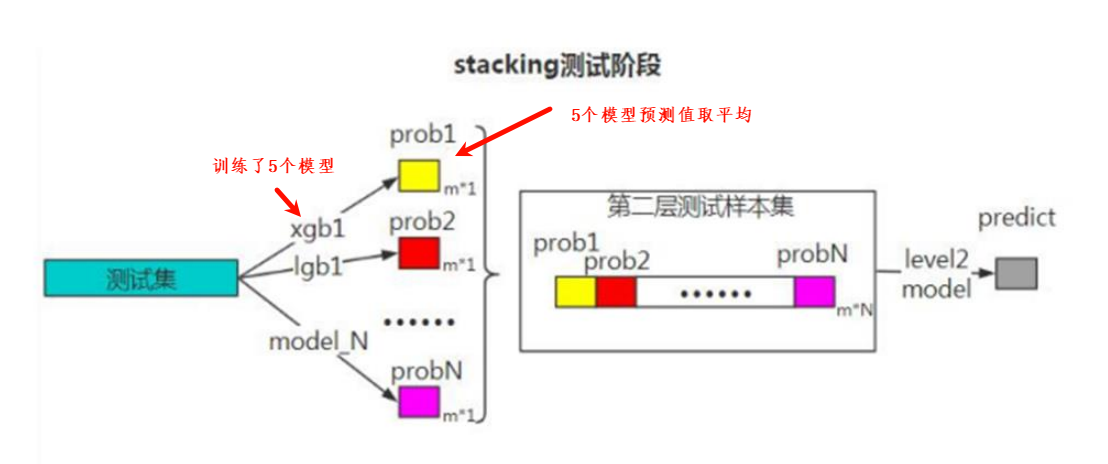
  • Stacking(有时候也称之为stacked generalization)是指训练一个模型用于组合(combine)其他各个模型。即首先我们先训练多个不同的模型，然后再以之前训练的各个模型的输出为输入来训练一个模型，以得到一个最终的输出。
  • 如果可以选用任意一个组合算法，那么理论上，Stacking可以表示前面提到的各种
    Ensemble方法。然而，实际中，我们通常使用单层logistic回归(分类问题)或者Ridge(回归问题)作为组合模型。
  • 注意：Stacking有两层，一层是不同的基学习器（classifiers/regressors）， 第二个是用于组合基学习器的元学习器（meta_classifier/meta_regressor

2.2 python代码实现

python 复制代码 
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import LinearSVC
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.ensemble import StackingClassifier, GradientBoostingClassifier
from sklearn.model_selection import train_test_split
import time
import matplotlib.pyplot as plt
import matplotlib as mpl

mpl.rcParams['font.sans-serif'] = [u'simHei']

X, y = load_iris(return_X_y=True)
estimators = [ # 两个基学习器
     ('rf', RandomForestClassifier(n_estimators=10, random_state=42)),  #  随机森林
     ('svr', make_pipeline(StandardScaler(), LinearSVC(random_state=42)))  # SVR分类器
]
# stacking、softmax、gbdt、rf 数据集在四个模型中的对比
stacking = StackingClassifier( # stacking算法
     estimators=estimators, final_estimator=LogisticRegression()
)
softmax = LogisticRegression(C=0.1, solver='lbfgs', multi_class='multinomial', fit_intercept=False)  # multinomial多分类
gbdt = GradientBoostingClassifier(learning_rate=0.1, n_estimators=100, max_depth=3)
rf = RandomForestClassifier(max_depth=5, n_estimators=150)

X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)

scores_train = []
scores_test = []
models = []
times = []

for clf, modelname in zip([softmax, gbdt, rf, stacking],
                          ['softmax', 'gbdt', 'rf', 'stacking']):
     print('start:%s' % (modelname))
     start = time.time()
     clf.fit(X_train, y_train) # .score(X_test, y_test)  # 训练
     end = time.time()
     score_train = clf.score(X_train, y_train)
     score_test = clf.score(X_test, y_test)
     scores_train.append(score_train)
     scores_test.append(score_test)
     models.append(modelname)
     times.append(end - start)

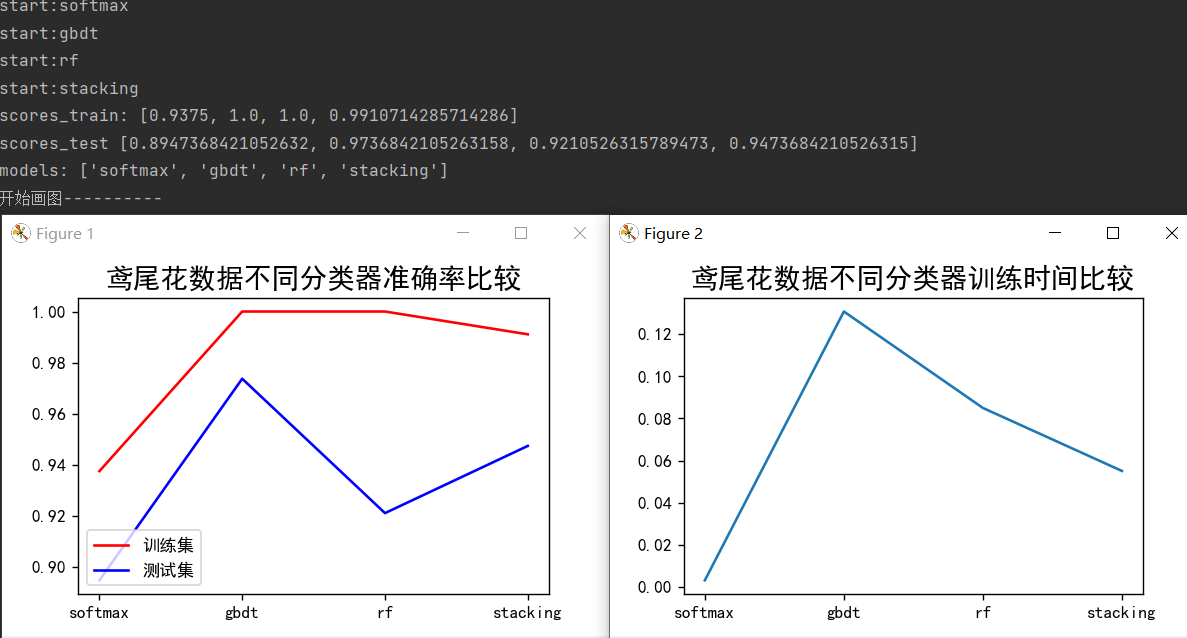
print('scores_train:', scores_train)
print('scores_test', scores_test)
print('models:', models)
print('开始画图----------')

plt.figure(num=1)
plt.plot([0, 1, 2, 3], scores_train, 'r', label=u'训练集')
plt.plot([0, 1, 2, 3], scores_test, 'b', label=u'测试集')
plt.title(u'鸢尾花数据不同分类器准确率比较', fontsize=16)
plt.xticks([0, 1, 2, 3], models, rotation=0)
plt.legend(loc='lower left')

plt.figure(num=2)
plt.plot([0, 1, 2, 3], times)
plt.title(u'鸢尾花数据不同分类器训练时间比较', fontsize=16)
plt.xticks([0, 1, 2, 3], models, rotation=0)
plt.show()

运行结果：

相关推荐
lqqjuly1 小时前
《AI Agent智能体与MCP开发实战》之构建个性化的arXiv科研论文MCP服务实战
人工智能·深度学习
羊仔AI探索1 小时前
GLM-4.6接入Claude Code插件，国内丝滑编程
ide·人工智能·ai·aigc·ai编程
Bdygsl1 小时前
数字图像处理总结 Day 1
人工智能·算法·计算机视觉
墨染星辰云水间1 小时前
机器学习（一）
人工智能·机器学习
张彦峰ZYF1 小时前
Coze文章仿写：智能体 + 工作流实现内容自动生成与插图输出
人工智能·ai·coze dify
Jerry.张蒙1 小时前
SAP传输请求流程：从开发到生产的安全流转
大数据·网络·人工智能·学习·职场和发展·区块链·运维开发
Lethehong1 小时前
openGauss在教育领域的AI实践：基于Java JDBC的学生成绩预测系统
java·开发语言·人工智能·sql·rag
山科智能信息处理实验室1 小时前
PCDreamer：基于多视角扩散先验的点云补全
人工智能
LDG_AGI1 小时前
【推荐系统】深度学习训练框架（六）：PyTorch DDP（DistributedDataParallel）数据并行分布式深度学习原理
人工智能·pytorch·分布式·python·深度学习·算法·spark
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04BongoCat - 跨平台键盘猫动画工具05Linux下V2Ray安装配置指南06本地部署阿里最新开源的Z-Image07Meta第三代“分割一切”模型——SAM 3本地部署教程：首支持文本提示分割，400万概念、30毫秒响应，检测分割追踪一网打尽08Gemini 3.0 Pro Preview 实测报告0946个Nano-banana 精选提示词，持续更新中10【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连