参数优化—序列神经网络

序列数据处理是深度学习领域中的重要研究方向，广泛应用于自然语言处理、语音识别、时间序列分析等任务。在序列神经网络的设计与训练中，参数初始化和归一化技术扮演着至关重要的角色，直接影响模型的收敛速度、泛化能力以及最终性能。参数初始化决定了网络的初始状态，而归一化技术则通过调整网络的输入分布来加速训练过程并缓解梯度消失或爆炸问题。

近年来，随着深度学习模型复杂度的不断提高，特别是在处理长序列数据时，传统的参数初始化和归一化方法面临着新的挑战。研究者们提出了一系列改进的技术，如零值初始化、Xavier 初始化、He 初始化、批归一化、层归一化等，这些方法在序列建模任务中取得了显著的效果。同时，针对序列数据的特点，研究者们也在不断探索新的初始化和归一化策略，以提高序列神经网络的性能和稳定性。

参数初始化技术

零值初始化

零值初始化是一种简单直接的参数初始化方法，将神经网络的所有权重和偏置初始化为零。这种方法在传统观点中被认为是无效的，因为它会导致网络对称性无法打破，使得所有神经元在训练过程中表现相同。然而，近年来的研究表明，在特定条件下，零值初始化可以取得与随机初始化相当甚至更好的效果。

在序列神经网络中，零值初始化面临着更大的挑战，因为序列数据的处理需要网络能够捕捉时间依赖关系。然而，最近的研究提出了几种改进的零值初始化方法，使得其在序列建模任务中变得可行。

零值初始化的理论基础

零值初始化的理论基础在于，通过适当的网络结构设计和训练策略，可以打破对称性并实现有效的学习。传统观点认为，零初始化会导致所有神经元的梯度相同，从而无法进行有效的参数更新。然而，最新研究表明，在某些条件下，特别是在具有残差连接的网络中，零初始化可以通过利用网络的结构特性来打破对称性。

研究者提出，随机初始化可以被视为零初始化框架中的一个特例，通过引入适当的扰动来打破对称性。这种观点为零初始化提供了新的理论基础，并开辟了新的研究方向。

零值初始化在序列神经网络中的应用

在序列神经网络中，零值初始化的应用主要集中在具有残差连接的架构中。2024 年提出的 ZerO 初始化方法证明，在残差网络中使用全零和全一的初始化可以在多种图像分类数据集上取得最先进的性能。这一发现挑战了传统的随机初始化方法，并为序列模型的初始化提供了新思路。

在循环神经网络 (RNN) 中，零值初始化的应用较为有限，因为 RNN 的循环连接容易导致梯度消失或爆炸问题。然而，最新研究表明，在特定条件下，零值初始化可以与其他技术结合使用，如梯度截断或自适应学习率，以提高 RNN 的训练稳定性。

零值初始化的最新进展

2024 年，研究者提出了 "完全相同初始化"(IDInit) 方法，该方法利用类似单位矩阵的结构来有效保持残差网络中主层和子层之间的恒等映射。这种方法通过填充类似单位矩阵的矩阵来解决非方阵权重矩阵中的秩约束问题，并使用随机梯度下降改进了传统单位矩阵的收敛问题。IDInit 在各种设置中增强了稳定性和性能，包括大规模数据集和深度模型。

同年，另一项研究重新评估了零值初始化在深度学习中的有效性，挑战了近五十年来 AI 社区认为零初始化对神经网络无效的误解。研究表明，通过引入适当的方法，即使所有权重和偏置都初始化为零，也能实现成功的学习。实验结果表明，零初始化在多层感知机、卷积神经网络、残差网络、视觉 Transformer 和多层感知机混合器等多种模型中可以匹配甚至超过随机初始化的性能。

此外，零值初始化在注意力机制中的应用也取得了进展。2024 年的研究表明，零初始化注意力可以作为一种有效的微调技术，特别是在序列建模任务中。研究人员证明，零初始化注意力与专家混合模型之间存在联系，并表明线性和非线性提示以及门控函数都可以被最优估计。

随机初始化

随机初始化是深度学习中最常用的参数初始化方法，通过从适当分布中随机采样来初始化网络参数。这种方法能够打破网络的对称性，使不同神经元能够学习不同的特征。随机初始化的关键在于选择合适的分布和参数，以确保信号在网络中的稳定传播。

随机初始化的理论基础

随机初始化的理论基础主要来源于信号传播理论。在深度神经网络中，如果初始化分布的方差不合适，可能导致信号在网络中传播时出现梯度消失或爆炸问题。为了解决这一问题，研究者提出了多种随机初始化方法，如均匀分布初始化、高斯分布初始化等，这些方法通过调整分布的参数来控制信号的方差。

在序列神经网络中，随机初始化面临额外的挑战，因为信号需要在时间维度上传播。循环神经网络中的梯度消失和爆炸问题尤为严重，这使得选择合适的初始化方法变得更加关键。

随机初始化在序列神经网络中的应用

在循环神经网络中，随机初始化通常使用均匀分布或高斯分布。对于传统的 RNN，通常将权重矩阵初始化为小随机值，以避免梯度爆炸。对于 LSTM 和 GRU 等门控循环单元，通常使用更复杂的初始化策略，如将输入到隐藏层的权重矩阵使用均匀分布初始化，而将隐藏层到隐藏层的权重矩阵使用正交初始化。

在 Transformer 架构中，随机初始化通常使用 Xavier或 He 初始化方法，这些方法能够更好地适应自注意力机制的特性。同时，位置编码的初始化也非常重要，通常使用正弦或余弦函数来初始化位置编码，以捕捉序列中的位置信息。

随机初始化的最新进展

2025 年，研究者提出了一种名为 "因子化随机合成器"(Factorized Random Synthesizer) 的方法，该方法通过因子化随机矩阵来初始化神经网络。这种方法在序列建模任务中表现出色，特别是在处理长序列时，能够有效减少计算复杂度并提高模型性能。

同年，另一项研究探索了随机初始化 Transformer的算法能力，发现即使 Transformer 模型是随机初始化的，仅训练输入和输出嵌入层，也能在各种任务上表现出色。这一发现挑战了传统观点，为序列模型的初始化提供了新的思路。

此外，2025 年提出的 RWKV-7"Goose" 架构扩展了增量规则，纳入了向量值状态门控、自适应上下文学习率和改进的值替换机制。这些改进增强了表达能力，实现了有效的状态跟踪，并允许识别所有正则语言，超越了在标准复杂性假设下 Transformer 的理论能力。

Xavier 初始化

Xavier 初始化（也称为 Glorot 初始化）是由 Xavier Glorot 和 Yoshua Bengio 在 2010 年提出的一种参数初始化方法，旨在解决深度神经网络中的梯度消失和爆炸问题。该方法基于信号传播理论，通过调整初始化分布的方差，使得信号在前向传播和反向传播过程中保持稳定的方差。

Xavier 初始化的理论基础

Xavier 初始化的理论基础是信号传播的方差保持原则。假设网络中的每一层都是线性的，并且激活函数是线性的或双曲正切函数 (tanh)，那么为了保持信号在前向传播和反向传播过程中的方差稳定，权重矩阵的方差应该设置为 2/(n_in + n_out)，其中 n_in 是输入神经元的数量，n_out 是输出神经元的数量。

Xavier 初始化通常使用均匀分布或高斯分布。对于均匀分布，参数范围设置为 [-sqrt (6/(n_in + n_out)), sqrt (6/(n_in + n_out))]；对于高斯分布，标准差设置为 sqrt (2/(n_in + n_out))。

Xavier 初始化在序列神经网络中的应用

在序列神经网络中，Xavier 初始化被广泛应用于各种架构，特别是在循环神经网络和 Transformer 中。在RNN 中，Xavier 初始化通常用于初始化输入到隐藏层和隐藏层到隐藏层的权重矩阵，以确保信号在时间步之间的稳定传播。

在 LSTM 和 GRU 中，Xavier 初始化通常用于初始化输入门、遗忘门和输出门的权重矩阵，而循环连接的权重矩阵则通常使用正交初始化，以提高训练的稳定性。

在 Transformer 架构中，Xavier 初始化被用于初始化自注意力机制中的查询、键和值矩阵，以及前馈网络中的权重矩阵。这种初始化方法能够有效减少训练过程中的梯度波动，提高模型的收敛速度。

Xavier 初始化的最新进展

2024 年，研究者提出了局部稳定性条件 (Local Stability Condition, LSC) 理论，该理论扩展了现有的稳定性理论，涵盖了更广泛的深度循环网络家族。研究表明，经典的 Glorot (即 Xavier)、He 和正交初始化方案在应用于前馈全连接神经网络时满足 LSC 条件。然而，在分析深度循环网络时，研究者发现了一种新的指数爆炸源，这种爆炸源来自于深度和时间的矩形网格中的梯度路径计数。为了缓解这一问题，研究者提出了一种新方法，对梯度的时间和深度贡献赋予一半的权重，而不是传统的一权重。

此外，2025年的研究表明，Xavier 初始化在处理长序列时可能存在局限性，特别是在 Transformer 架构中。为了解决这一问题，研究者提出了几种改进的初始化方法，如频率偏置调整的 Xavier 初始化，能够更好地捕捉数据中的不同时间尺度。

He 初始化

He 初始化（也称为 Kaiming 初始化）是由何恺明等人在 2015 年提出的一种参数初始化方法，特别适用于使用 ReLU 激活函数的深度神经网络。该方法是对 Xavier 初始化的改进，能够更好地处理 ReLU 函数的非对称性和零中心特性。

He 初始化的理论基础

He 初始化的理论基础同样基于信号传播的方差保持原则，但针对 ReLU 激活函数进行了优化。由于 ReLU 函数在负区间的输出为零，导致激活值的方差在传播过程中会减半。为了补偿这一效应，He 初始化将权重矩阵的方差设置为 2/n_in，其中 n_in 是输入神经元的数量。

He 初始化通常使用均匀分布或截断高斯分布。对于均匀分布，参数范围设置为 [-sqrt (6/n_in), sqrt (6/n_in)]；对于截断高斯分布，标准差设置为 sqrt (2/n_in)。

He 初始化在序列神经网络中的应用

在序列神经网络中，He 初始化主要应用于使用 ReLU 或其变体作为激活函数的架构。在基于 ReLU 的 RNN 中，He 初始化用于初始化输入到隐藏层和隐藏层到隐藏层的权重矩阵，以确保信号在时间步之间的稳定传播。

在 Transformer 架构中，He 初始化被广泛应用于前馈网络部分，特别是当使用 ReLU 或 GELU 激活函数时。研究表明，使用 He 初始化可以显著提高 Transformer 在长序列建模任务中的性能，如语言建模和机器翻译。

在基于深度学习的语音识别系统中，He 初始化也被证明是有效的，特别是在处理长语音序列时，能够减少梯度消失问题并提高模型的训练稳定性。

He 初始化的最新进展

2024 年，研究者提出了一种基于特征分解的循环神经网络初始化方法，该方法在 tanh-RNN、LSTM 和 GRU 上的性能优于 Xavier 初始化和 Kaiming 初始化（即 He 初始化）以及其他仅 RNN 的初始化方法，如 IRNN 和 sp-RNN。该方法基于对权重矩阵的特征分解，提供了对隐藏状态空间的新视角，并解释了激活函数中保留信息的功能。

同年，另一项研究提出了 GradInit 方法，这是一种自动化且与架构无关的神经网络初始化方法。GradInit 基于一个简单的启发式方法：调整每个网络层的范数，使得使用规定超参数的 SGD 或 Adam 的单步能够产生最小的可能损失值。该方法在各种卷积架构中加速了收敛和测试性能，无论是否具有跳跃连接，甚至在没有归一化层的情况下也是如此。GradInit 还提高了原始 Transformer架构在机器翻译中的稳定性，使得可以使用 Adam 或 SGD 而无需学习率预热。

此外，2023 年的一项调查研究全面概述了深度学习中的参数初始化技术，包括经典方法和最新进展。该研究讨论了这些技术的理论基础、经验性能及其在各种神经网络架构中的应用，并强调了该领域的开放挑战和未来研究方向。

归一化技术

批归一化

批归一化 (Batch Normalization, BN) 是由 Sergey Ioffe 和 Christian Szegedy 在 2015 年提出的一种归一化技术，旨在解决深度学习中的内部协变量偏移问题。该技术通过在每个小批量数据上标准化激活值，使网络训练更加稳定，并允许使用更高的学习率。

批归一化的理论基础

批归一化的理论基础是内部协变量偏移 (Internal Covariate Shift) 的概念，指的是随着网络参数的更新，各层输入分布的变化。这种分布变化会导致训练困难，因为网络需要不断适应新的分布。

批归一化通过在每个小批量数据上计算均值和方差，并对激活值进行标准化，来减少内部协变量偏移。具体来说，对于输入数据 x，批归一化计算：

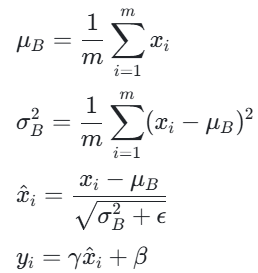
其中，μB和σB2是小批量数据的均值和方差，x^i是标准化后的值，γ和β是可学习的缩放和平移参数，ϵ是一个小常数，用于防止除零错误。

批归一化在序列神经网络中的应用

在序列神经网络中，批归一化的应用面临一些挑战，特别是在处理变长序列和动态计算图时。传统的批归一化在每个时间步独立地应用归一化，这可能导致时间步之间的信息丢失。

为了解决这些问题，研究者提出了几种适用于序列数据的批归一化变体。其中一种方法是在循环神经网络的输入到隐藏层转换中应用批归一化，这可以有效减少输入分布的变化，提高训练稳定性。

另一种方法是在 LSTM 单元中应用批归一化。传统的 LSTM 单元在输入到隐藏层的转换中应用批归一化，而 2019 年提出的增强型 LSTM 与批归一化 (E-LSTM-BN) 方法成功地将批归一化集成到 LSTM 单元的更新中，在序列学习任务中实现了比 LSTM 及其变体更快的收敛速度和更高的分类准确率。

此外，研究者还提出了循环批归一化 (Recurrent Batch Normalization) 方法，该方法对 LSTM 进行了重新参数化，将批归一化的好处带到循环神经网络中。与以往仅将批归一化应用于 RNN 的输入到隐藏层转换的工作不同，该方法证明了对隐藏到隐藏转换进行批归一化是可能且有益的，从而减少了时间步之间的内部协变量偏移。

批归一化的最新进展

2024 年，研究者提出了上下文感知批归一化 (Context-Aware Batch Normalization, CABN) 方法，这是一种新颖的方法，通过结合来自输入序列的上下文信息，使批归一化适应序列数据。CABN 使用轻量级注意力机制基于每个时间步的局部上下文动态调整归一化参数。在各种序列建模任务上的实验结果表明，CABN 优于传统的批归一化和其他归一化技术。

同年，另一项研究提出了高效批归一化 (Efficient Batch Normalization, EBN) 方法，这是批归一化的修改版本，可以高效地处理变长序列。EBN 独立计算每个时间步的统计信息，允许在同一批次中处理不同长度的序列。在各种序列建模任务上的评估表明，EBN 优于传统的批归一化和其他用于变长序列的归一化技术。

此外，2024 年的一项调查研究回顾了批归一化的最新进展，重点关注解决其在特定场景中的局限性的方法，如小批量大小、动态架构和序列数据。该研究讨论了批归一化的各种修改和替代方法，包括层归一化、实例归一化、组归一化及其变体，并探讨了批归一化及其变体的理论基础及其在不同领域的应用。

层归一化

层归一化 (Layer Normalization, LN) 是由 Jimmy Lei Ba、Jamie Ryan Kiros 和 Geoffrey E. Hinton 在 2016 年提出的一种归一化技术，特别适用于循环神经网络和序列建模任务。与批归一化不同，层归一化在单个样本的特征维度上进行归一化，而不是在小批量的样本维度上进行归一化，这使得它更适合处理批量大小可变的序列数据。

层归一化的理论基础

层归一化的理论基础与批归一化类似，都是为了减少内部协变量偏移，加速网络训练。然而，层归一化的计算方式与批归一化有很大不同。对于输入数据 x，层归一化计算：

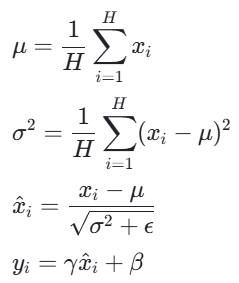
其中，H 是特征维度的大小，μ和σ2是沿着特征维度计算的均值和方差，γ和β是可学习的缩放和平移参数，ϵ是一个小常数，用于防止除零错误。

与批归一化不同，层归一化在每个样本的特征维度上独立计算均值和方差，因此不受批量大小的影响，这使得它特别适合处理序列数据，尤其是在批量大小可变或较小的情况下。

层归一化在序列神经网络中的应用

层归一化在序列神经网络中得到了广泛应用，特别是在循环神经网络和 Transformer 架构中。研究表明，层归一化比批归一化更有效地训练 RNN 在序列建模任务上，如语言建模和语音识别。

在 LSTM 和 GRU 等循环单元中，层归一化可以应用于输入门、遗忘门和输出门的计算，以减少内部协变量偏移，提高训练稳定性。在这种情况下，层归一化通常在每个时间步独立应用，计算当前时间步的输入和隐藏状态的均值和方差。

在 Transformer 架构中，层归一化是标准组件，通常应用于多头注意力模块和前馈网络模块的输出，以稳定训练过程。与批归一化不同，层归一化在 Transformer 中表现出色，特别是在处理长序列时，能够有效减少梯度消失问题。

此外，层归一化还可以用于训练难以用其他归一化技术训练的深层 RNN。研究表明，层归一化可以帮助训练非常深的 RNN，这些 RNN 在使用其他归一化技术时难以训练。

层归一化的最新进展

2024 年，研究者提出了自适应层归一化 (Adaptive Layer Normalization, ALN) 方法，该方法基于序列中每个元素的时间位置自适应地调整归一化参数。ALN 使用一个小型前馈网络来预测每个时间步的缩放和平移参数，使模型能够捕捉数据中随时间变化的统计特性。在各种时间序列预测任务上的评估表明，ALN 优于传统的层归一化和其他归一化技术。

同年，另一项研究提出了元素 wise 层归一化 (Elementwise Layer Normalization, ELN) 方法，这是对 2025 年提出的动态 tanh (DyT) 方法的数学推导和改进。研究表明，DyT 可以作为层归一化的替代，但缺乏理论基础。通过去掉某些近似，研究者获得了一种替代的元素 wise 变换，称为元素 wise 层归一化 (ELN)。实验表明，ELN 比 DyT 更准确地类似于层归一化。

此外，2025 年的一项研究提出了混合归一化 (HybridNorm) 方法，旨在通过混合归一化技术实现稳定高效的 Transformer 训练。该研究探讨了 Transformer 归一化层和语义子空间的独立性，提出了一种新的归一化框架，结合了不同归一化方法的优点。

最后，2024 年的一项研究提出了动态归一化 (Dynamic Normalization, DN) 框架，这是一个用于序列数据的统一框架，结合了批归一化和层归一化的优点。DN 根据输入序列的特征（如长度和统计特性）自适应地在不同归一化策略之间切换。研究表明，DN 可以有效处理变长序列，并在各种序列建模任务上优于现有的归一化技术。

序列神经网络中的参数优化策略

序列数据的挑战

序列数据具有时间依赖性和可变长度的特点，这给参数初始化和归一化带来了特殊的挑战。在序列神经网络中，信号需要在时间维度上传播，这使得梯度消失和爆炸问题更加严重。此外，序列数据的长度可能各不相同，这使得批归一化等依赖固定批量大小的技术难以应用。

在循环神经网络中，这些挑战尤为明显。传统的 RNN 在处理长序列时表现不佳，因为梯度在反向传播过程中会指数级增长或衰减。LSTM 和 GRU 等门控循环单元通过引入门控机制部分解决了这一问题，但仍然面临训练困难，特别是在处理非常长的序列时。

在 Transformer 架构中，虽然自注意力机制可以有效捕捉长距离依赖关系，但参数初始化和归一化仍然是关键问题。研究表明，适当的初始化和归一化可以显著提高 Transformer 在长序列建模任务上的性能。

初始化策略的优化

针对序列数据的特点，研究者提出了多种初始化策略的优化方法。在循环神经网络中，研究者提出了基于特征分解的初始化方法，该方法分析了权重矩阵的特征值和特征向量，提供了对隐藏状态空间的新视角。这种方法在 tanh-RNN、LSTM 和 GRU 上的性能优于传统的 Xavier 初始化和 Kaiming 初始化。

在 Transformer 架构中，研究者提出了多种初始化策略，如频率偏置调整的 HiPPO 初始化，能够更好地捕捉数据中的不同时间尺度。此外，2025 年提出的持久性初始化 (Persistence Initialization) 方法，通过确保未训练模型的初始输出与简单基准模型的输出相同，提高了时间序列预测模型的训练稳定性。

对于状态空间模型 (SSMs)，研究者发现 SSMs 表现出一种隐式偏差，更有效地捕捉低频分量而非高频分量。研究表明，SSM 的初始化赋予了其固有的频率偏差，而传统方式训练模型不会改变这种偏差。基于这一理论，研究者提出了两种调整频率偏差的机制：通过缩放初始化来调整固有频率偏差；或通过应用基于 Sobolev 范数的滤波器来调整梯度对高频输入的敏感性，从而通过训练改变频率偏差。

归一化策略的优化

为了应对序列数据的挑战，研究者提出了多种归一化策略的优化方法。在循环神经网络中，层归一化被证明比批归一化更有效，特别是在处理长序列时。此外，研究者还提出了在 LSTM 单元中应用批归一化的方法，如增强型 LSTM 与批归一化 (E-LSTM-BN)，在序列学习任务中实现了更快的收敛速度和更高的分类准确率。

在 Transformer 架构中，层归一化是标准组件，但研究者也提出了多种改进方法。例如，2024 年提出的上下文感知批归一化 (CABN) 方法，通过结合来自输入序列的上下文信息，使批归一化适应序列数据。CABN 使用轻量级注意力机制基于每个时间步的局部上下文动态调整归一化参数，在各种序列建模任务上表现出色。

对于时间序列预测任务，研究者提出了自适应层归一化 (ALN) 方法，该方法基于序列中每个元素的时间位置自适应地调整归一化参数。ALN 使用一个小型前馈网络来预测每个时间步的缩放和平移参数，使模型能够捕捉数据中随时间变化的统计特性。

此外，2024 年提出的动态归一化 (DN) 框架，结合了批归一化和层归一化的优点，根据输入序列的特征（如长度和统计特性）自适应地在不同归一化策略之间切换。DN 在各种序列建模任务上优于现有的归一化技术，特别是在处理变长序列时表现出色。