目录
[1. 需要B树和B+树原因](#1. 需要B树和B+树原因)
[2. B树(B-树)](#2. B树(B-树))
[2.1. 命名](#2.1. 命名)
[2.2. 特性](#2.2. 特性)
[2.3. 操作](#2.3. 操作)
[3. B+树](#3. B+树)
[3.1. 操作](#3.1. 操作)
1. 需要B树和B+树原因
针对二叉搜索树进行了平衡化的,AVL树和红黑树使得查找、插入、删除数据的效率均降到了log n级别。但是这三位呢,通常都是先把数据全部加载到内存里面,然后在内存中进行处理的数据量,通常不会很大。内存,目前的容量呢一般都在GB级别。比如说现在比较常见的4G8G或者16G。
如果要处理的数据规模非常大,大到内存根本存不下了的时候。那这个时候呢咱们就只能先给它存到硬盘里头 ,因为没办法把大规模的数据全部读到内存当中,所以只能分批次的把需要处理的数据,从硬盘调到内存里进行进一步处理。
为什么一定要读到内存里头呢?不能直接在硬盘上面操作这些数据吗?
操作数据是需要CPU去执行相关的指令的,CPU是不能直接和硬盘进行交互的。硬盘里的数据呢必须先调到内存里头,才能进一步和CPU进行交互。
对数据进行相关的一些处理,那把这个过程呢称作一次硬盘访问 ,也可以叫做一次硬盘IO 。然而这个访问速度是非常慢 ,内存的单次访问时间是纳秒级,但是硬盘的访问呢却是毫秒级(一毫秒等于100万纳秒)。硬盘的访问时间成本是比较高的,访问的次数肯定是越少越好。
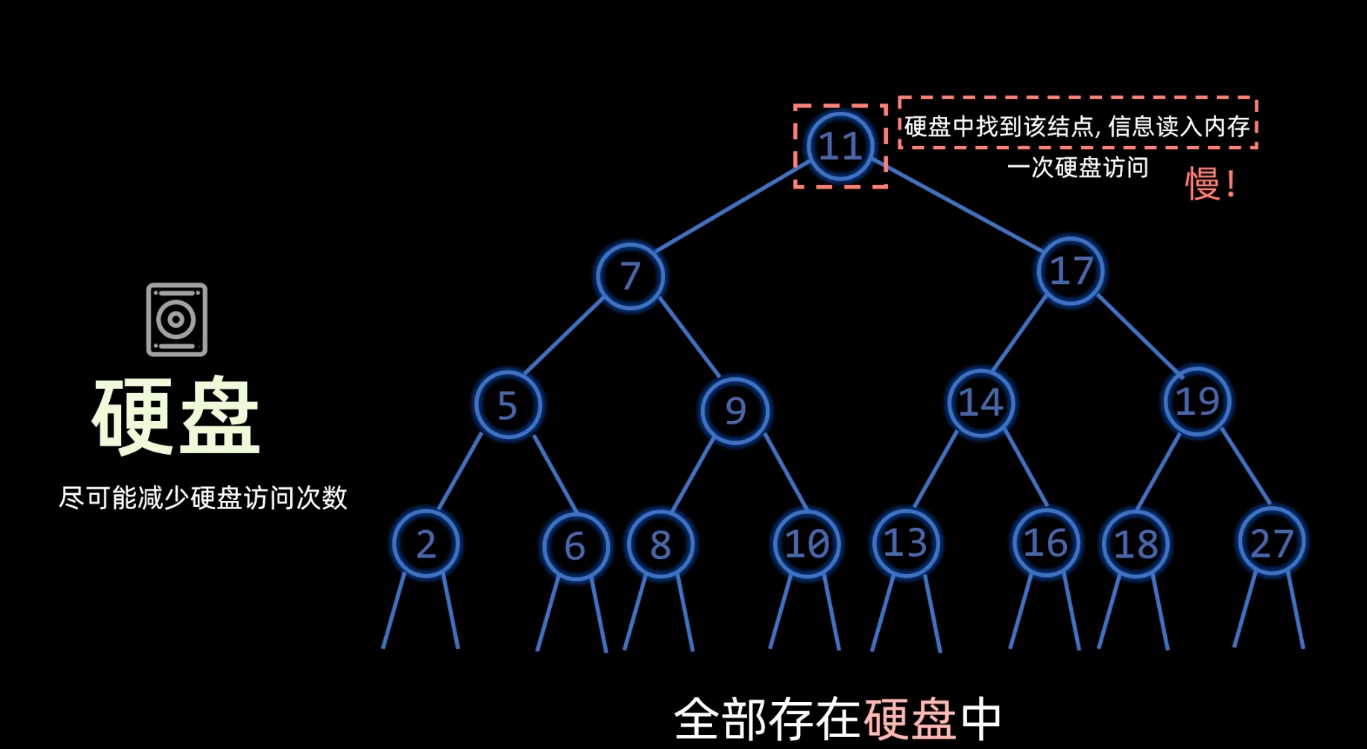
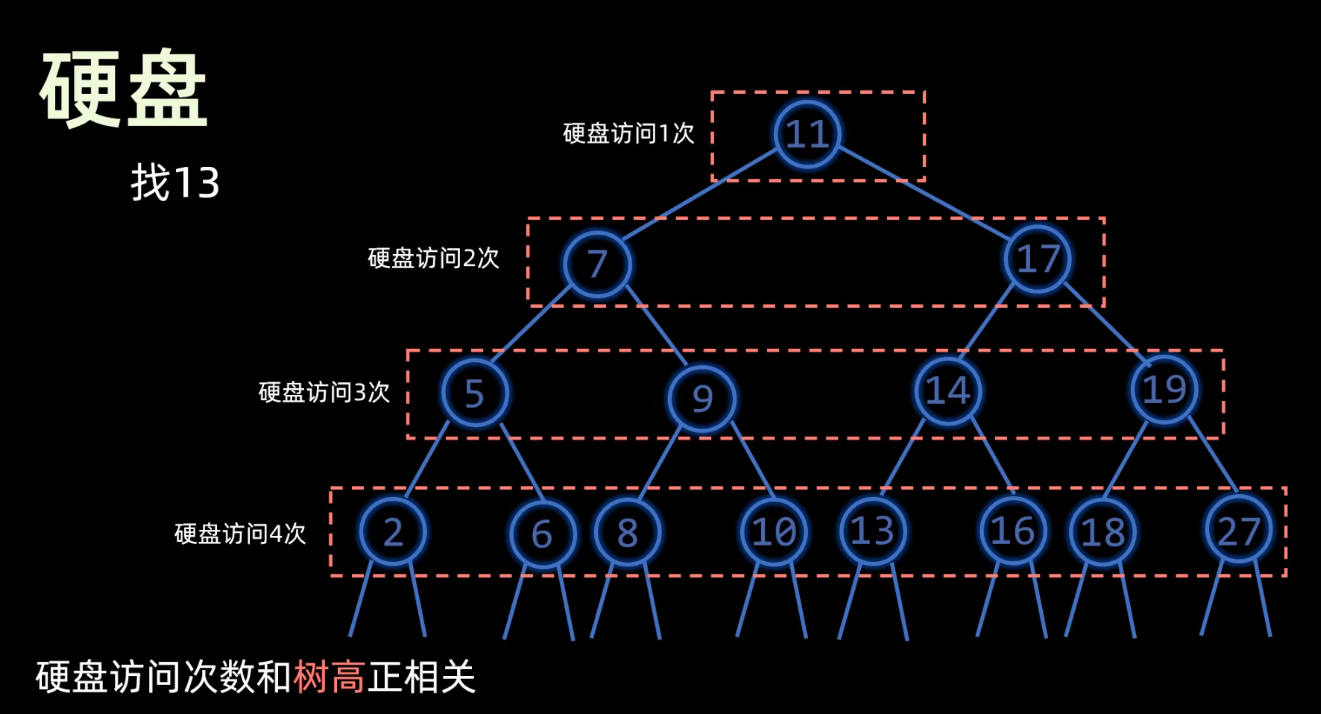
2. B树(B-树)
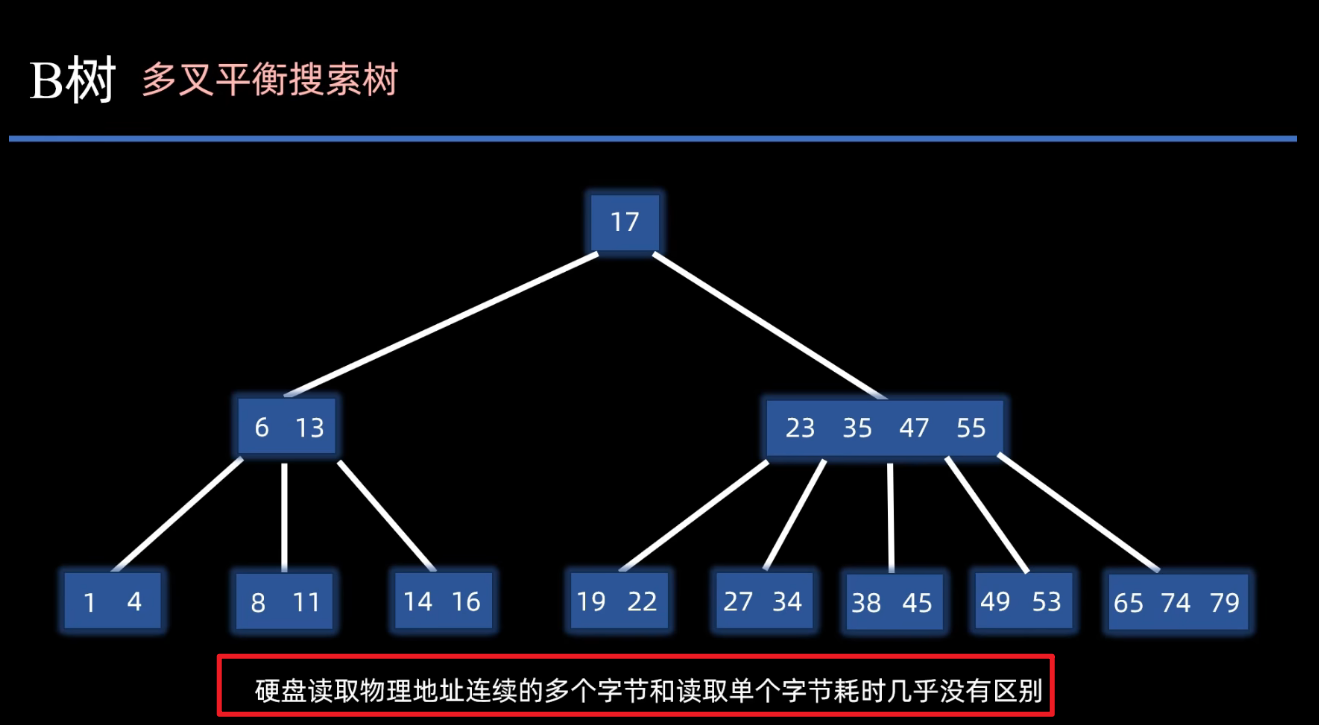
访问节点 是在硬盘上进行,结点内的数据 操作是在内存中进行。
2.1. 命名
有x个分叉称之为 x阶B树
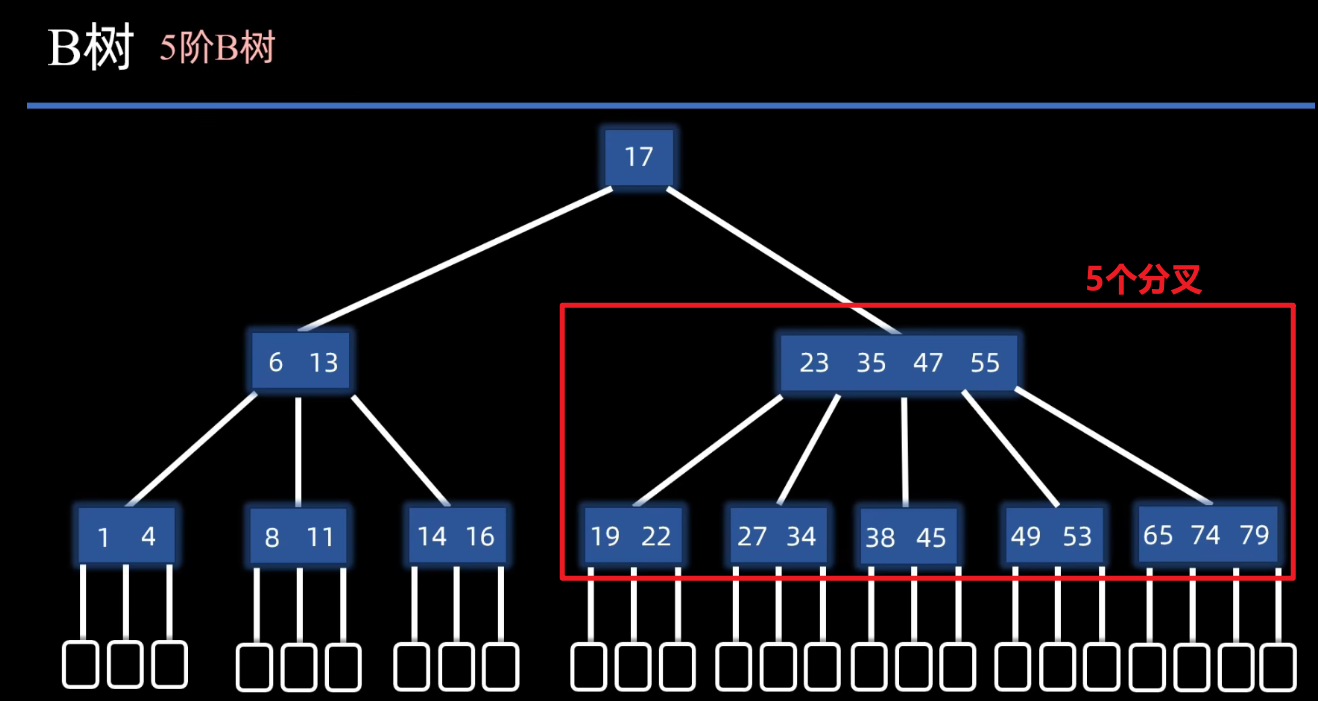
最下面还有一层空节点 ,咱们把这个包含数据的节点呢称为内部节点 ,那下面这些空节点称为外部节点 。这些外部节点哈并没有任何信息哈,他们只是**意味着查找失败,**也叫做失败节点。
关于B树的叶子节点,有的地方呢会把最下面的失败节点叫做叶节点 ,也有的地方把内部节点的最后一层叫做叶节点,本博客后续统一称呼内部节点的最后一层,为叶子节点。
2.2. 特性
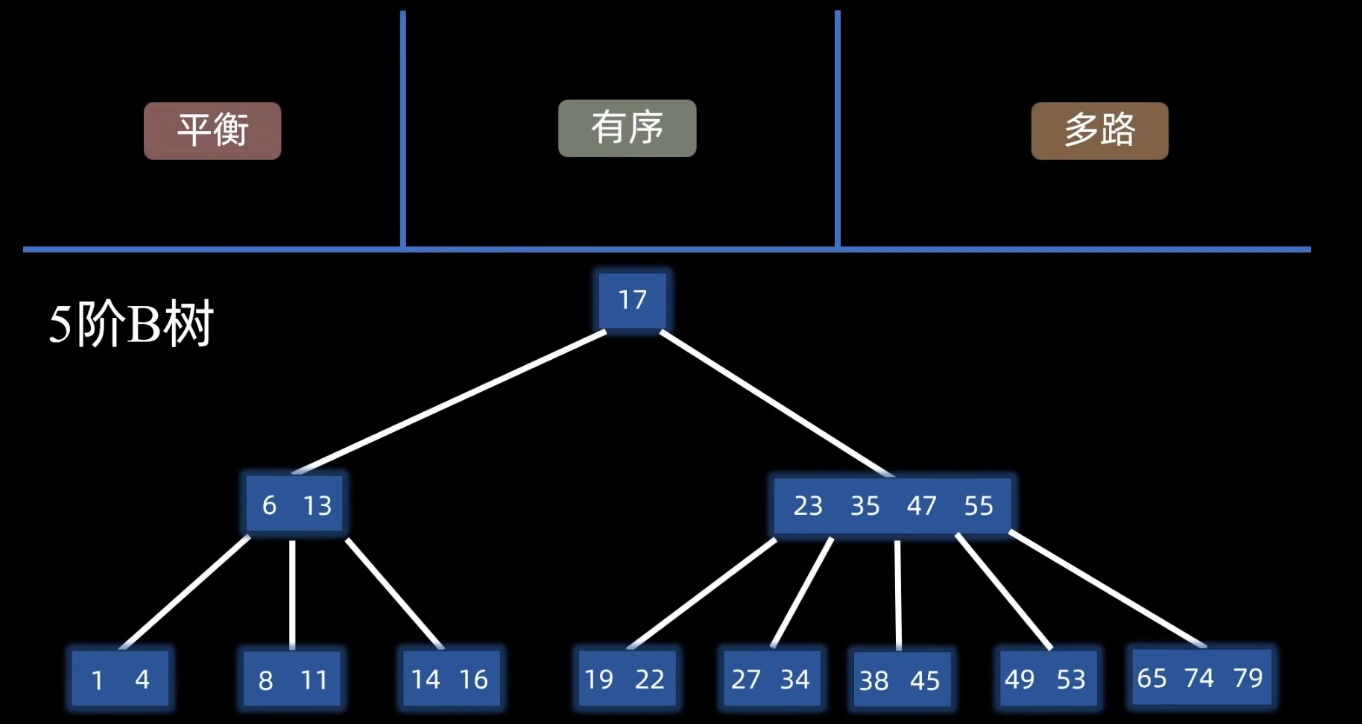
- 平衡: 所有的叶节点都在同一层
- 有序: 结点内有序,也就是任一元素的左子树都小于该元素,右子树大于该元素。
- **多路:**关于m阶B树的结点:
(向上取整,取大于这个的数的最小值)
2.3. 操作
插入

删除
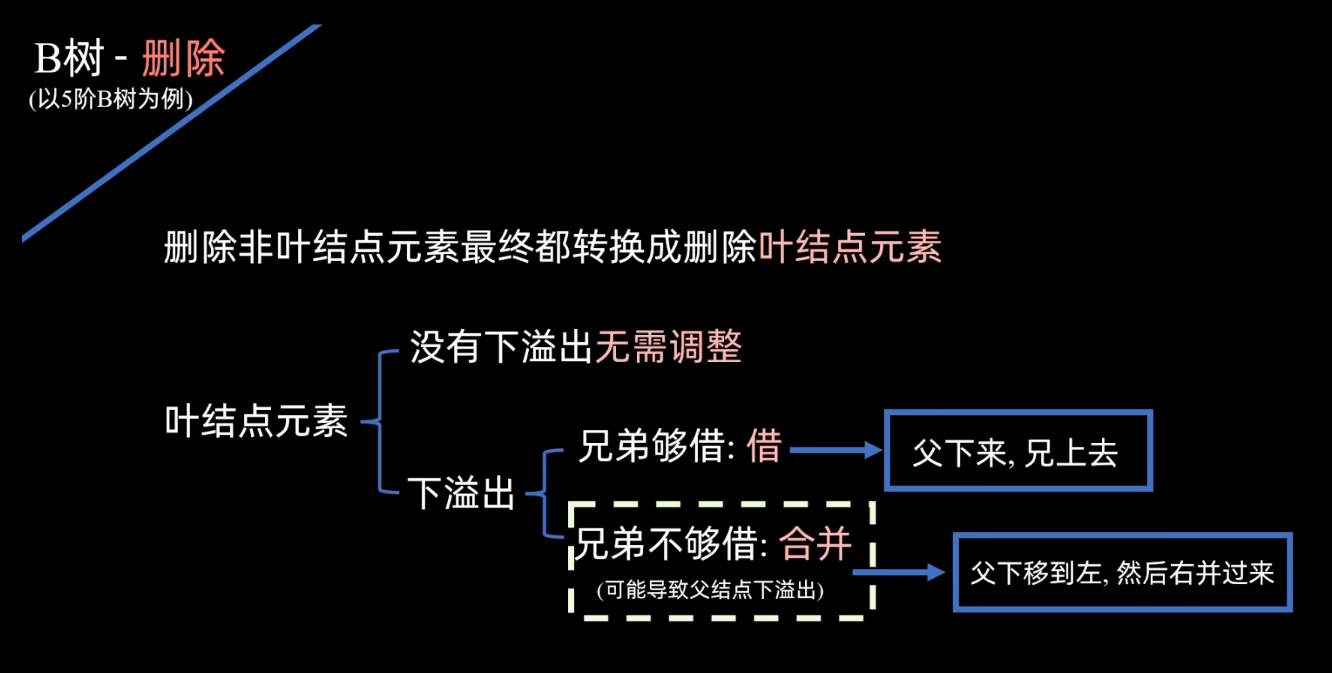
删除的操作,比较容易出现下溢出 的情况。因为删除会少一个元素嘛,所以可能会低于节点元素个数的下限。
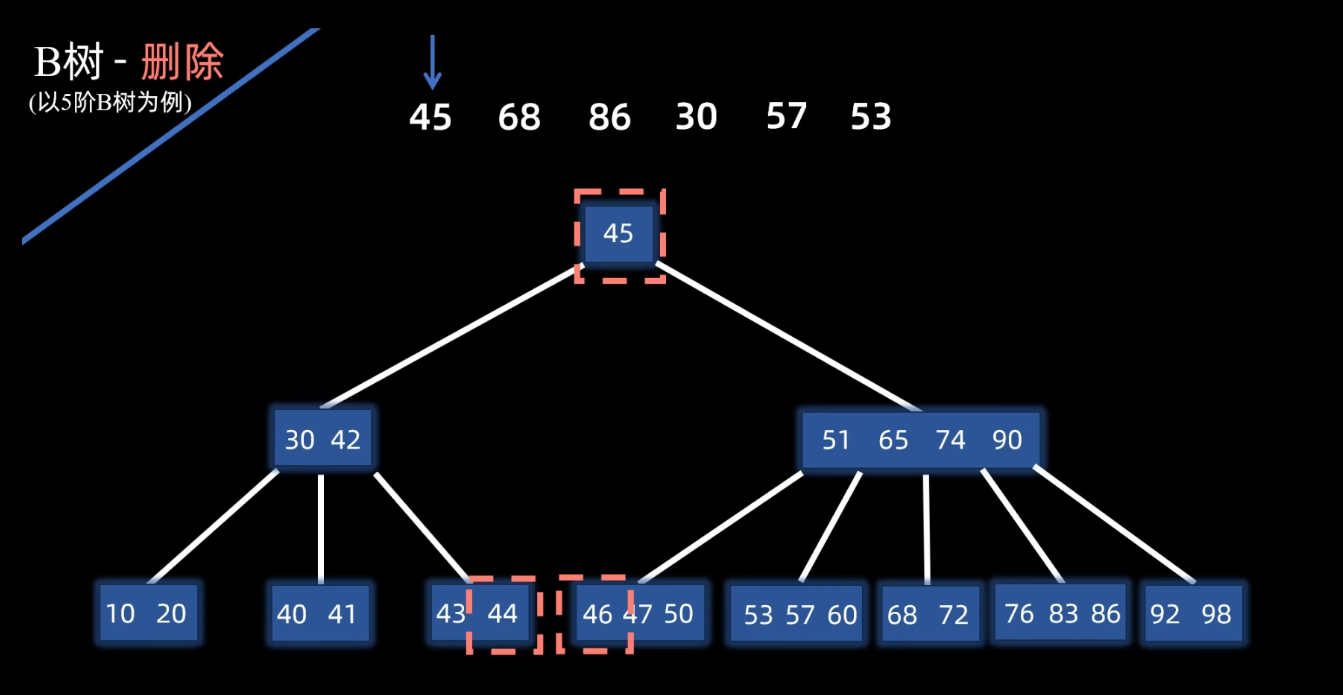
如果删除的是非叶节点上的元素,那需要按照类似于二叉搜索树,左右子树都有的情况,也就是用它的直接前驱或者后继去替换它 。
比如说45的直接前驱呢是44,也就是他左子树中最大的;那直接后继呢是46,也就是他右子树中最小的。
不管是前驱还是后继,都一定落在叶子节点上,那这两个咱们选一个去替换那个45。
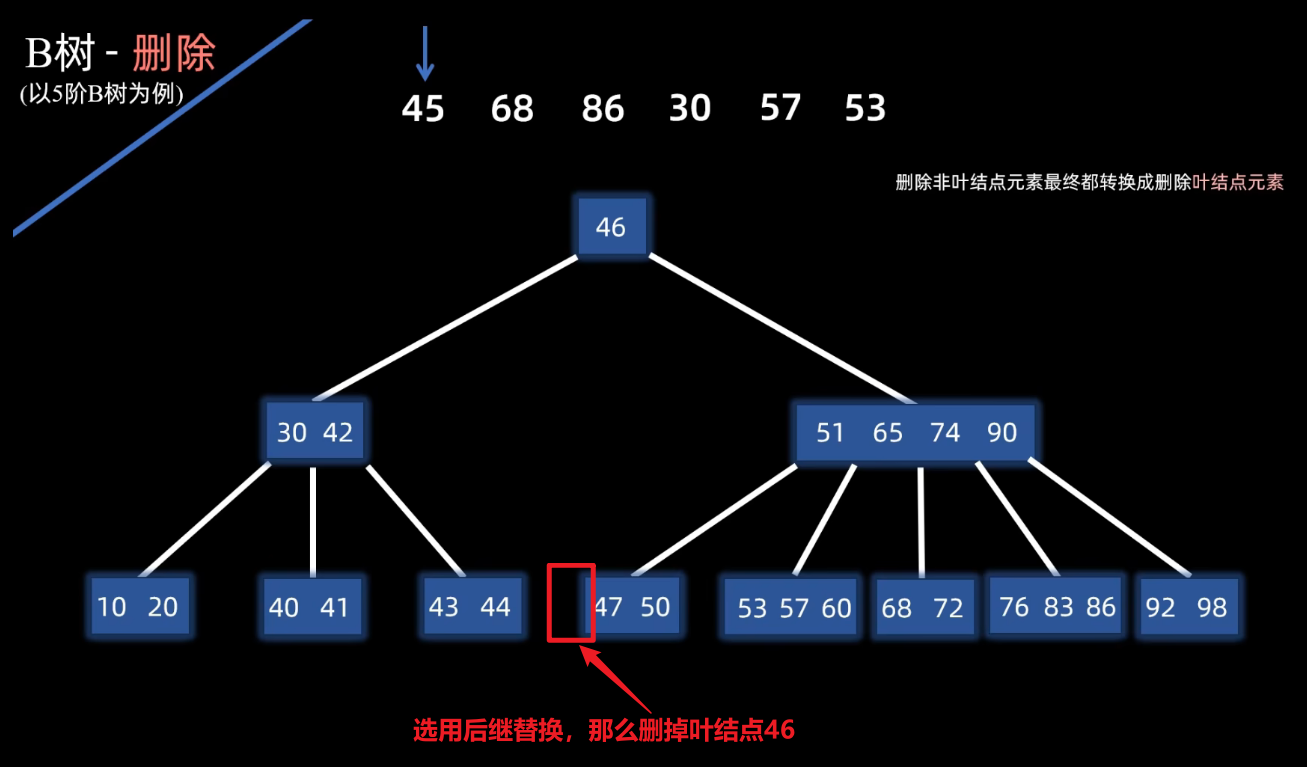
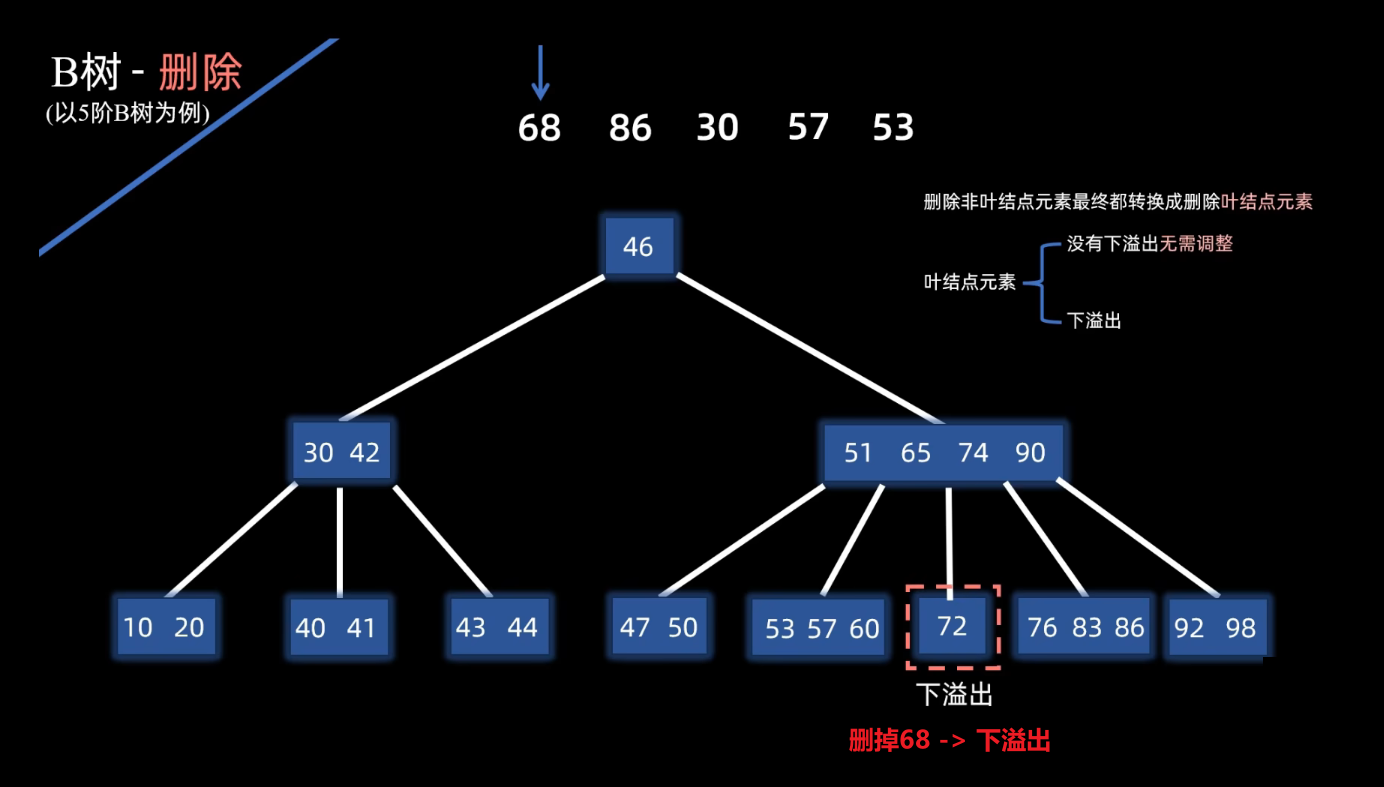
发现出现了下溢出 ,这个时候,尝试和左右兄弟借一个元素 过来。要先看看兄弟够不够借,现在他的左右兄弟呢都有三个元素,就是说都可以借给他一个。那随便选一个兄弟借,左右都可以。当然有时候可能只有左兄弟或者只有右兄弟够 元素借。那就找那个够借的去借。
删除操作总结
- 首先如果删除的是非叶节点上的元素 ,那就先通过前驱或者后继的替换转换成删除叶节点上的元素
- 那如果删除的是叶节点上的元素 ,那么就直接删掉 ,删除之后看看有没有出现下溢出,如果没有下溢出,那不需要任何调整
- 如果下溢出 ,那就需要看左右兄弟够不够借 ,如果兄弟够借元素,那具体来说:就是父元素下移到下一处的节点,然后兄弟元素上去
- 那左右兄弟都不够借 的话,那就需要执行合并操作 ,那具体来说:就是父亲元素先下移到左边的节点,然后右边的节点再合并过来。
- 合并完之后,父节点可能出现连锁反应,也跟着下溢出,那就需要继续看兄弟够不够借,继续进行调整。
- 那如果根节点空 呢,就需要释放掉根节点 ,让合并出来的节点成为新的根节点
3. B+树
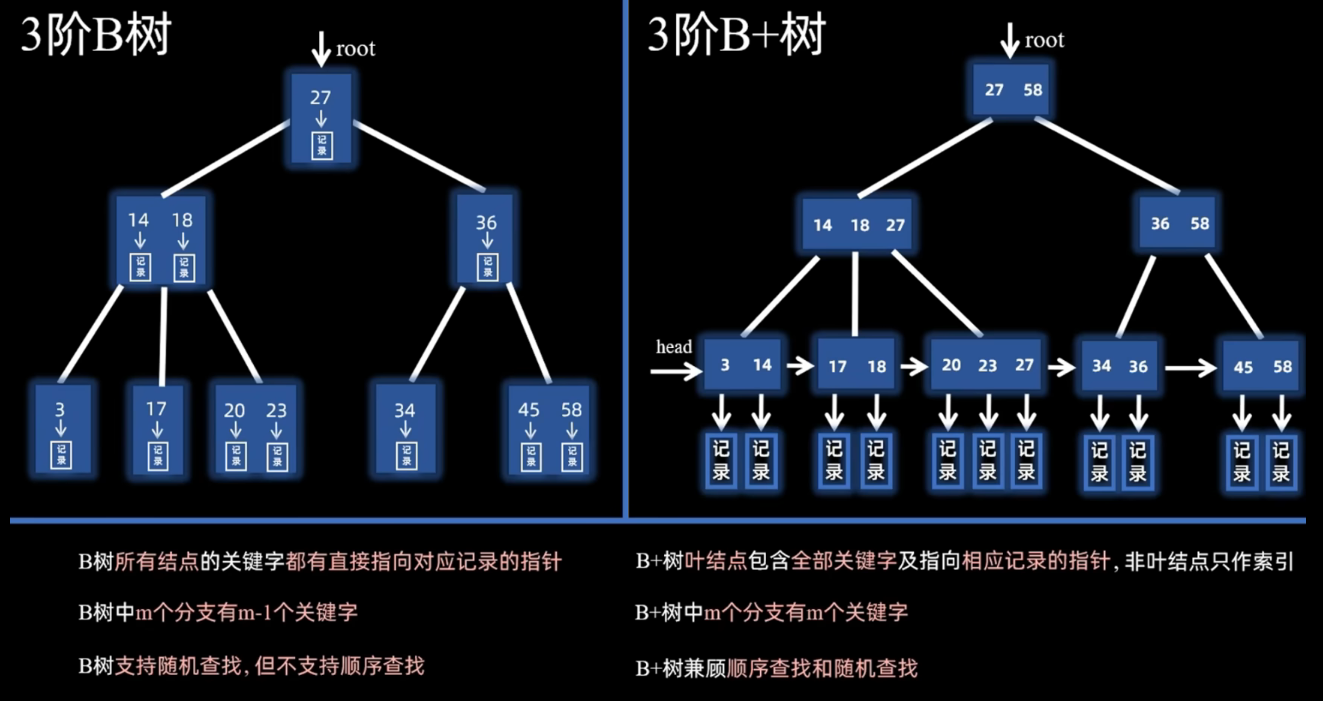
B+树的叶节点层包含了所有的元素 ,同时这些元素是从小到大排列,节点之间是用指针连接成了一个链表的结构 。这样可以很轻松地通过第一个节点前的头指针 来快速的对所有的元素进行顺序遍历 ,而不用像B数那样不得不采用中序遍历的方法,在结点之间来回穿梭,因此B+树常被用作数据库中的索引结构。
实际上每个元素都包含指向记录存储地址的指针 ,此时节点内的元素又被称作关键字 ,通过关键字包含的指针,咱们可以索引到数据库中的某一条记录。
其他的特性呢B树和B+树都是一样的。比如说所有的叶节点都在同一层 ,m阶B+数最多就会有m个分支 。那对于非根节点 ,最少得有一半有分支 ,一半如果不凑整,要向上取整。根节点 ,最少要有两个分支。
3.1. 操作
随机查找
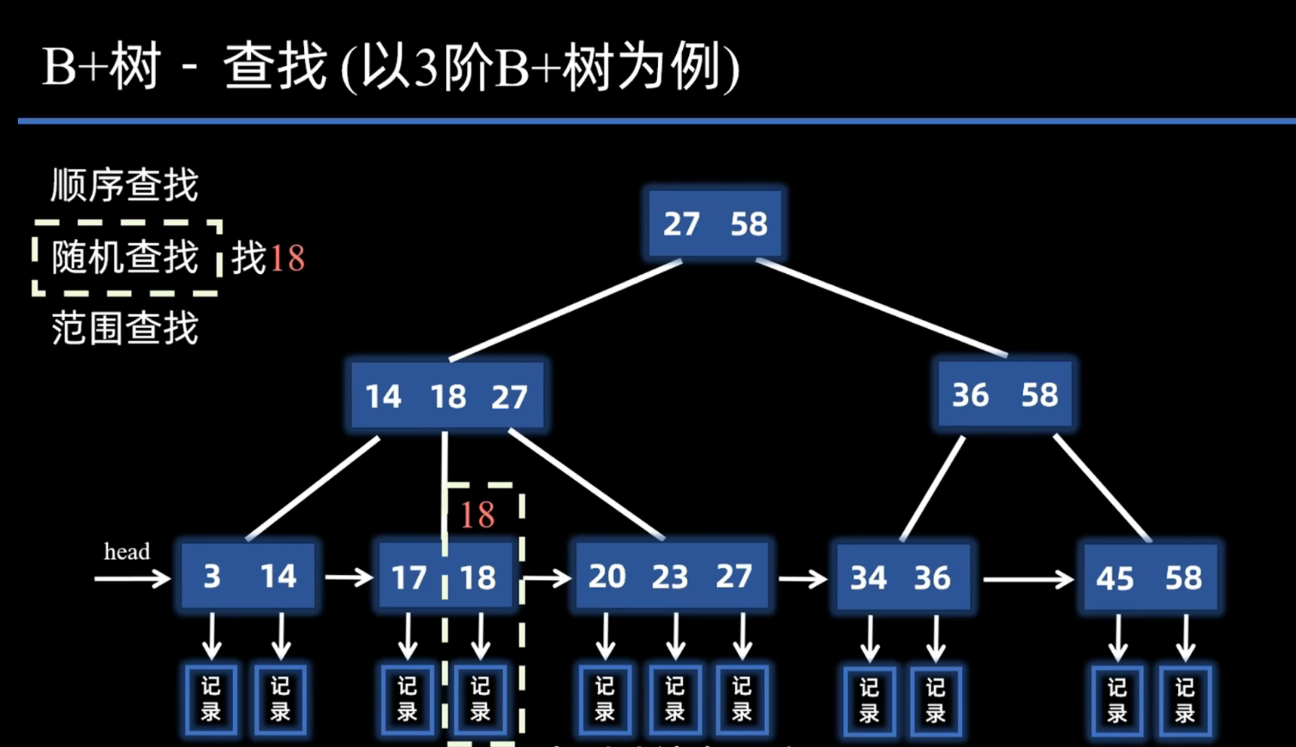
现在要找18对应的记录,先通过root指针找到根节点 ,将其读入内存后,拿18和27进行比较。发现比27小,就走27的子树,然后继续和14比较,发现大于14,那就继续往后。
此时呢发现似乎找到了18,但要注意此时遇到的18它只是用来索引 的,它本身并没有指向记录的指针 。所以说通过它是获取不到对应的记录的,还是需要继续走18的子树,也就是走到叶节点层和17进行比较。发现大于17,继续往后。此时可以通过18这个关键字,索引到对应数据文件中的记录。
因此说B+树的查找,最终一定会落在叶子节点上 ,因为只有叶节点层的关键字 能索引到对应的记录,如果在非叶节点上遇到了相同的关键字,那咱们还是需要继续往下查找,直到叶节点层。
范围查找
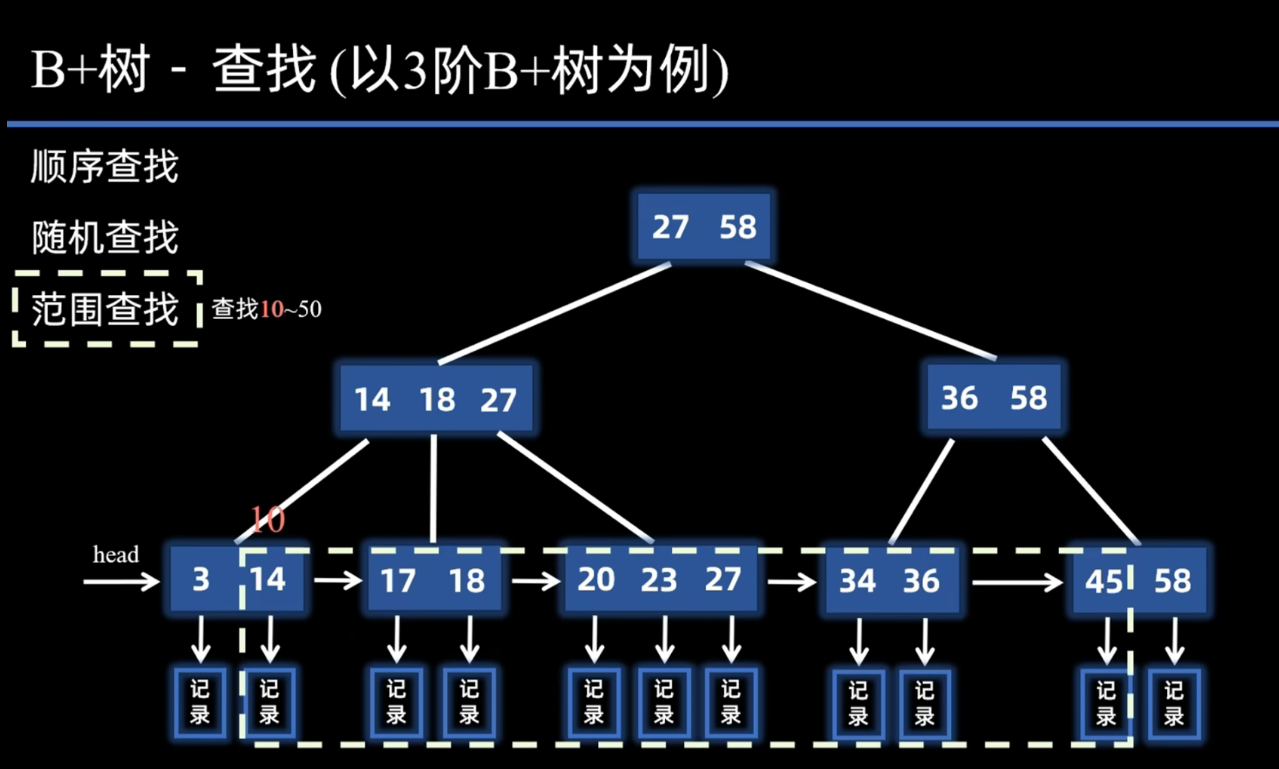
比如要找范围在10~50的所有关键字的记录:
那可以先找到范围起点的位置 ,也就是先找一下10,那还是一样。先和根节点 中的27进行对比,那就走27的子树,然后呢比14小,那就继续往下发现比3大,往后继续。
这个时候发现比14小,同时现在处在叶子节点层, 那么就意味着10其实是不存在的。但是这并没有关系,此时意味着14就是10~50这个范围内的第一个关键字。 那就从14开始,接下来就只需要按照顺序依次往后遍历就可以,直到范围内的最后一个关键字45。
同时还可以通过指针获取到每个关键字对应的记录
