leetcode 3623. 统计梯形的数目 I 中等

圣保罗的大教堂2025-12-03 9:23

给你一个二维整数数组 points，其中 points[i] = [xi, yi] 表示第 i 个点在笛卡尔平面上的坐标。

水平梯形 是一种凸四边形，具有 至少一对水平边（即平行于 x 轴的边）。两条直线平行当且仅当它们的斜率相同。

返回可以从 points 中任意选择四个不同点组成的 水平梯形数量。

由于答案可能非常大，请返回结果对 10^9 + 7 取余数后的值。

示例 1：

输入： points = $\[1,0$ , $2,0$ , $3,0$ , $2,2$ , $3,2$ ]

输出： 3

解释：

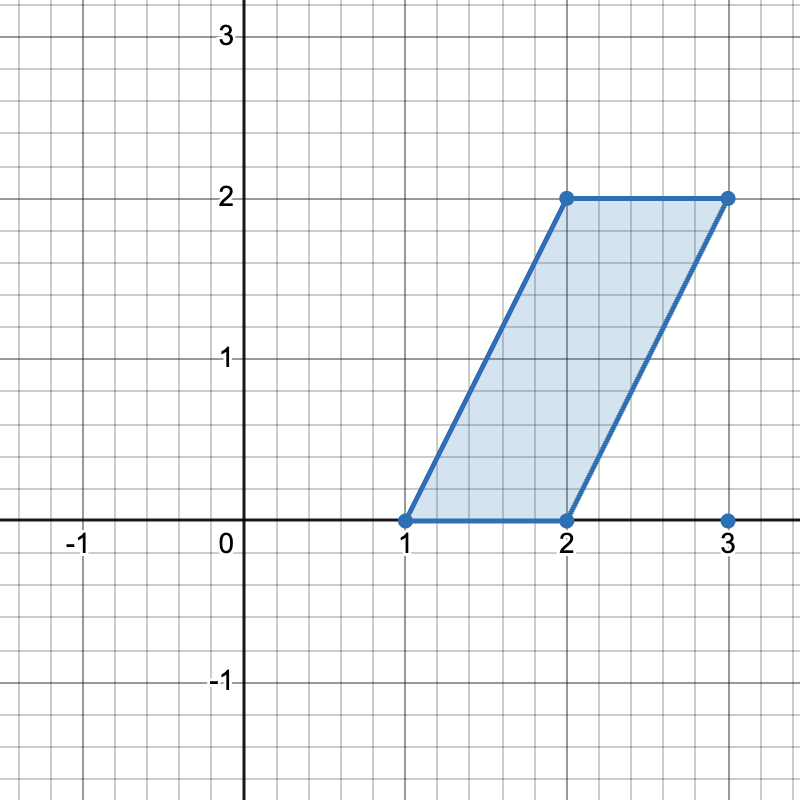
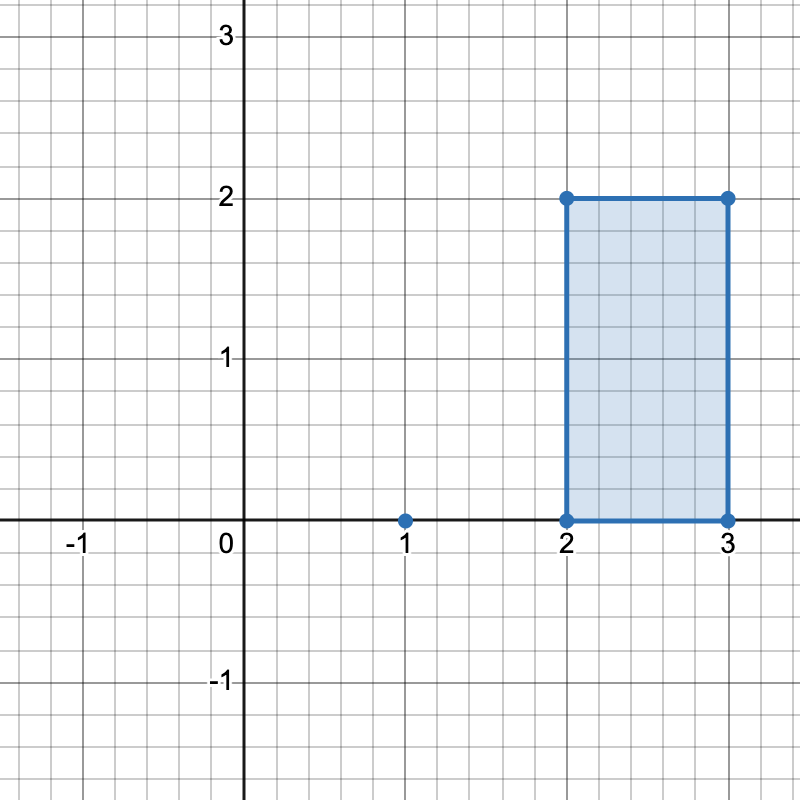
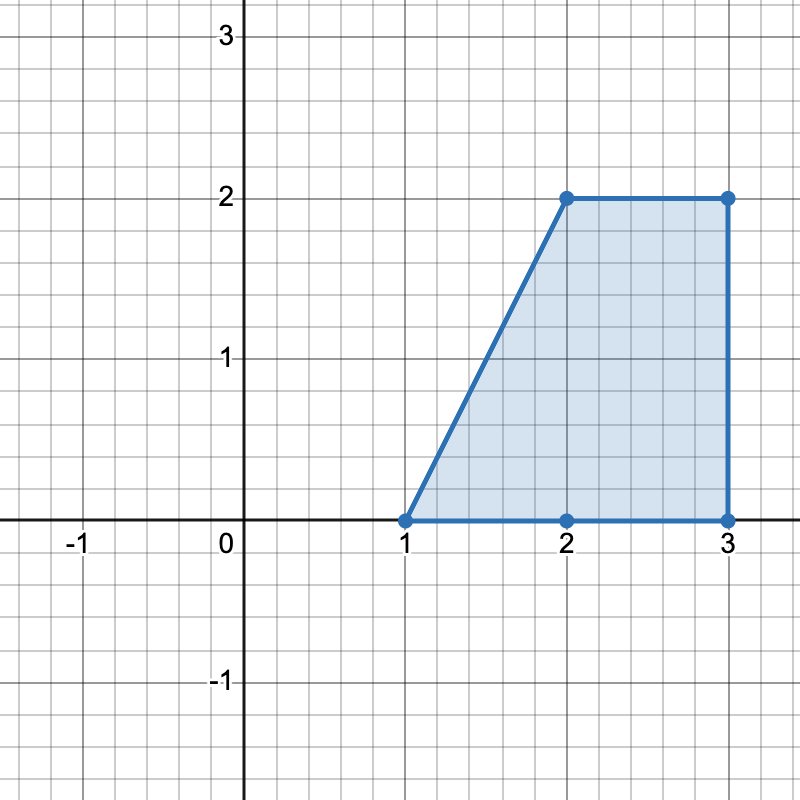
有三种不同方式选择四个点组成一个水平梯形：

使用点 [1,0]、[2,0]、[3,2] 和 [2,2]。
使用点 [2,0]、[3,0]、[3,2] 和 [2,2]。
使用点 [1,0]、[3,0]、[3,2] 和 [2,2]。

示例 2：

输入： points = $\[0,0$ , $1,0$ , $0,1$ , $2,1$ ]

输出： 1

解释：

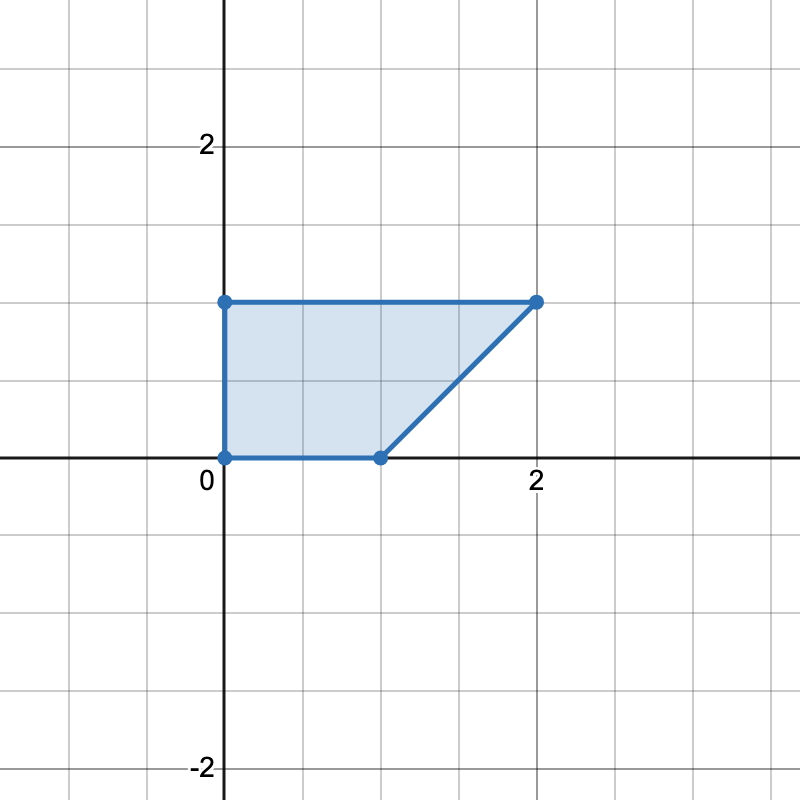
只有一种方式可以组成一个水平梯形。

提示：

4 <= points.length <= 10^5
--10^8 <= xi, yi <= 10^8
所有点两两不同。

分析：题目说明必须要具有至少一对平行于 x 轴的边才算作水平梯形。统计所有具有相同 y 坐标的点数量，之后遍历每一行，如果这一行有 c 个点，那么从 c 个点中选 2 个点，有 c*(c−1)/2 种选法，可以组成一条水平边，即梯形的顶边或底边。之后再取其它另一行，求出另一条水平边的数量 k，相乘后加入答案。

cpp 复制代码

class Solution {
public:
    int countTrapezoids(vector<vector<int>>& points) {
        int mod=1e9+7,n=points.size();
        map<int,int>mp;
        for(int i=0;i<n;++i)
            mp[points[i][1]]++;
            
        long long ans=0,sum=0;
        for(auto it:mp)
        {
            int x=it.second;
            long long temp=1LL*x*(x-1)/2;
            ans+=sum*temp;
            sum+=temp;
        }
        return ans%mod;
    }
};