【cpp知识铺子】map和set的前身-二叉搜索树

爱装代码的小瓶子2025-12-03 16:27

关注我，学习c++不迷路:

个人主页：爱装代码的小瓶子

专栏如下：

  1. c++学习
  2. Linux学习

后续会更新更多有趣的小知识，关注我带你遨游知识世界

期待你的关注。

文章目录

  • [1. 什么是二叉搜索树？](#1. 什么是二叉搜索树？)
  • [2. 二叉搜索树的实现：](#2. 二叉搜索树的实现：)
    • [2.1 不带val值（set）](#2.1 不带val值（set）)
      • [2.1.1 主要结构：](#2.1.1 主要结构：)
      • [2.2.2 插入：](#2.2.2 插入：)
      • [2.2.3 删除函数：](#2.2.3 删除函数：)
      • [2.2.4 其余函数：](#2.2.4 其余函数：)
    • 2.2带val值（map）
  • [3. 总结：](#3. 总结：)

1. 什么是二叉搜索树？

再数据结构中我们学过二叉树还有大小堆这种结构，而二叉搜索树也是一种特殊的结构，他的特点是：右节点永远比父亲节点大，而左节点永远比父亲节点小。这就导致这种树很适合来查找特定的值。

规则总结如下：

  1. 其左子树上所有节点的值都小于这个节点的值。
  2. 其右子树上所有节点的值都大于这个节点的值。
  3. 左子树和右子树也各自都是二叉搜索树。

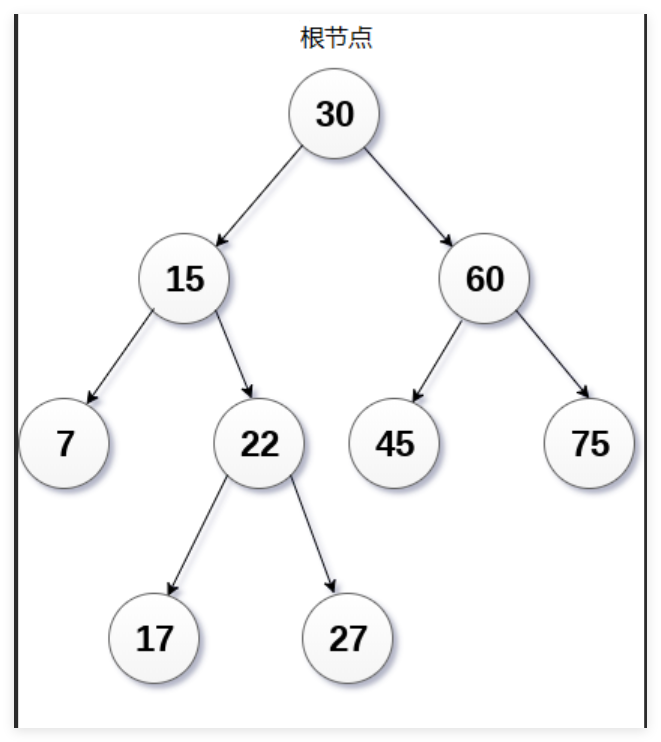
    这种规则在查找的时候巧妙的利用二分法来查找。

2. 二叉搜索树的实现：

2.1 不带val值（set）

2.1.1 主要结构：

cpp 复制代码 
template<class K>
struct BSTNode {
	BSTNode(const K& val)
		:_key(val)
		,_left(nullptr)
		,_right(nullptr)
	{}
	//注意底部接口公开：
	K _key;
	BSTNode<K>* _left;//注意指向左节点
	BSTNode<K>* _right;
};

注意这里我用了struct，这是因为底部接口时公开的。同时注意左节点和右节点都是存贮节点的地址。

cpp 复制代码 
template <class K>
class BSTree {
	//typedef BSTNode<K> Node;也可以用下面的：
	using Node = BSTNode<K>;
		private:
		node* _root = nullptr;
	};
}

再这里我们只需要顶一个根节点，同时后续的值我们将通过插入来完成，插入的同时可以new新的节点。

2.2.2 插入：

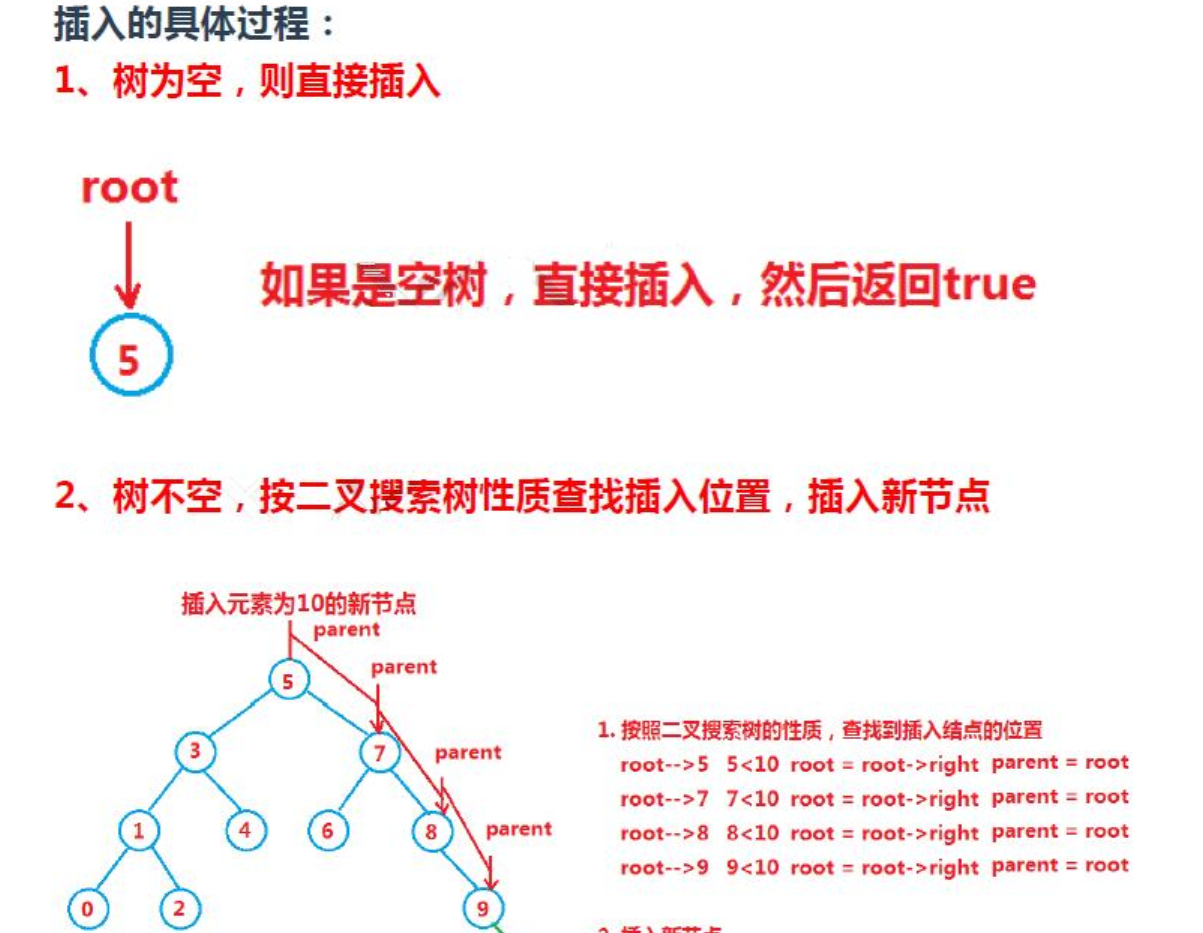
这个也是最主要的函数了，也是理解二叉搜索树的关键。我们在插入的一个值的时候，如果当前这个数为空，直接将new一个新的节点作为根节点。如果没有则进行比较，如果大就进入右子树，如果小则进入左子树，直至cur指向nullptr，同时还要不忘记定义一个变量parent，用来控制插入的方向。最后不要忘记比较一下，如果大就放在右边，如果小就放在parent的左边。

cpp 复制代码 
bool insert(const K& key)
{
	if (_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (key > cur->_key)
		{
			//如果大于就往右走；
			parent = cur;
			cur = cur->_right;
		}
		else if (key < cur->_key)
		{
			//如果小于就往左走；
			parent = cur;
			cur = cur->_left;
		}
		else {
			//相等则不进入。
			return false;
		}
	}
	cur = new Node(key);
	if (key > parent->_key)
		parent->_right = cur;
	else
		parent->_left = cur;
	return true;
}

2.2.3 删除函数：

这个也是比较难的，如果是在叶子节点就很简单，直接删除就好了，但是如果再非叶子节点，这该如何是好呢。我们可以看看这几种情况：

  • 第一种：最简单的：左右节点都为空
  • 第二种：左节点不为空，而右节点为空。
  • 第三种：与第二种恰巧相反，右节点不为空，而左节点为空
  • 第四种：也是最麻烦的，两个同时不为空。

他们的解决方式：

  1. 第一种其实可以归类到第二种或者第三种里面去，可以两个都没有，是可以当作瘸子的。我们可以删除父亲，请爷爷来托管孙子。这里其实也算比较简单的了
  2. 第二种就是父亲左右都不为空，这时候应该怎么办呢，相当于你有两个孙子，一个爷爷带不过来，这时候就需要请到保姆了。我们需要找寻cur右边最小的值，即（右子树最左边的数），随后交换位置。删除replace即可。同时注意链接replace后面的数。

替换法的精髓在于：找一个合适的"替身"来占据节点N的位置，这个替身的值放到N的位置后，能继续保持BST的性质，同时它本身易于被删除。

寻找合适的替身（R）

这个替身R需要满足一个关键条件：它的值必须大于N左子树的所有值，并且小于N右子树的所有值。这样，当R的值被放到N的位置时，整个树的排序关系依然成立。符合条件的有两个候选者：

前驱节点：节点N左子树中的最大值节点，即左子树中的"最右节点"。这个节点是N左子树中最大的，但依然小于N和N右子树的所有节点。

后继节点：节点N右子树中的最小值节点，即右子树中的"最左节点"。这个节点是N右子树中最小的，但依然大于N和N左子树的所有节点。

选择前驱或后继中的任意一个都可以。

"替代"的实际操作：值交换

所谓"用R替代N"，更准确的说法是 交换N和R的节点值。我们只把R的值复制到N的位置上，而N原本的左右孩子关系保持不变。这样，从值的角度来看，N已经被"删除"了（原本的值被覆盖），但树的结构暂时被修改了。

转化问题：删除节点R

完成值交换后，我们的目标就从"删除复杂的节点N"转变为"删除相对简单的节点R"。因为R是原BST中的前驱或后继，它必然具有一个关键特性：至多只有一个孩子。

前驱节点是左子树的最右节点，它不可能有右孩子（否则那个右孩子才会是更大的值，成为前驱）。

后继节点是右子树的最左节点，它不可能有左孩子（否则那个左孩子才会是更小的值，成为后继）。

因此，删除R就退化到了你提到的"情况2或情况3"，即删除一个叶子节点或仅有一个子节点的节点，这可以通过直接删除或子节点替换的方式轻松完成。

代码如下：

cpp 复制代码 
bool Erase(const K& key)
{
	if (_root == nullptr)
	{
		return false;
	}
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (key > cur->_key)
		{
			parent = cur;
			//如果大于就往右走；
			cur = cur->_right;
		}
		else if (key < cur->_key)
		{
			parent = cur;
			//如果小于就往左走；
			cur = cur->_left;
		}
		else {
			//准备删除工作：
			if (cur->_left == nullptr)
			{
				if (parent == nullptr)
				{
					_root = _root->_right;
				}
				else {
					if (cur == parent->_left)
						parent->_left = cur->_right;
					else
						parent->_right = cur->_right;
				}
				delete cur;
				return true;
			}
			else if (cur->_right == nullptr)
			{
				if (parent == nullptr)
				{
					_root = _root->_left;
				}
				else {
					if (cur == parent->_right)
						parent->_right = cur->_left;
					else
						parent->_left = cur->_left;
				}
				delete cur;
				return true;
			}

			else {
				Node* replace = cur->_right;
				Node* replaceParent = cur;
				while (replace->_left)
				{
					//找寻cur的最小右子树，即右子树的最左位置：
					replaceParent = replace;
					replace = replace->_left;
				}
				cur->_key = replace->_key;//赋值给cur
				// 已经在最左边了，只剩下右子树，满足上面的条件2：
				if (replaceParent->_right == replace)
					replaceParent->_right = replace->_right;
				else
					replaceParent->_left = replace->_right;
				delete replace;
				return true;
			}
		}
	}
	return false;//如果没有找到就是找寻失败。
}

2.2.4 其余函数：

我们已经完成了两个最难也是最重要的函数，就是insert函数和pop函数。此时我们可以再建立中序遍历函数，用来满足遍历二叉搜索树。中序遍历就是：左根右，这样排序出来也是有序的一个数组。

在数据结构专栏中我们已经讲过了，这也是分治思想的体现,我们先遍历左边，随后打印根，在遍历右边，如果遇到空，就开始返回。函数实现如下：

cpp 复制代码 
	void _InOrder(Node* root)
	{
		//对二叉搜索树的中序遍历：左根右.
		if (root == nullptr)
			return;
		_InOrder(root->_left);
		//当遇到空的时候返回执行打印该root的值。
		std::cout << root->_key << " ";
		_InOrder(root->_right);
	}

结果我们发现，我们我们无法访问根，这是因为在前面的结构我们也发现了_root是私有的，这时我们可以在封装一次。

cpp 复制代码 
	void InOrder()
	{
		//由于_root是私有，可以在包一层；
		_InOrder(_root);
		std::cout << std::endl;
	}

private:
	void _InOrder(Node* root)
	{
		//对二叉搜索树的中序遍历：左根右.
		if (root == nullptr)
			return;
		_InOrder(root->_left);
		//当遇到空的时候返回执行打印该root的值。
		std::cout << root->_key << " ";
		_InOrder(root->_right);
	}
	Node* _root = nullptr;//默认构造函数生成参数
};

这样就ok了，我们就可以完成对二叉搜索树完成遍历：

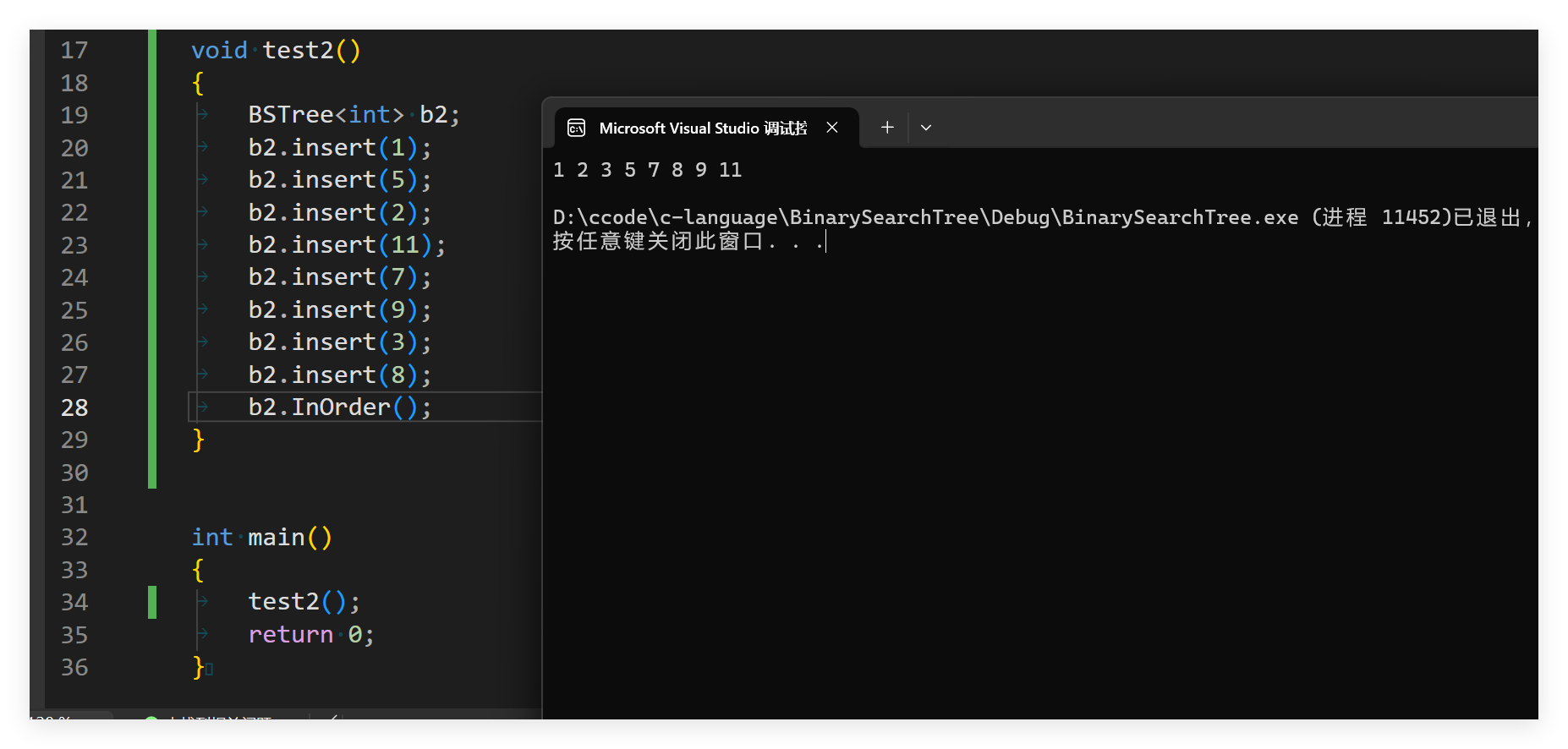
我们可以看出打印出来的数据是有序的，没有问题。

接下来是查询函数，查询指定的值。这样也很找，如果比根大就往右边找，如果小的化就往左边找，如果相等即可返回true。遇到空就是没有找到，最后返回false即可。还是比较简单的。我们来完成：

cpp 复制代码 
	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
				cur = cur->_right;
			else if (key < cur->_key)
				cur = cur->_left;
			else
				return true;
		}
		return false;
	}

2.2带val值（map）

这个我就简单讲讲，这个就加了val，大致的逻辑不变，我在find函数的时候会加一些打印出val值。

我直接给出代码：

cpp 复制代码 
namespace wwh {
	template<class K,class T>
	struct BSNode {
		BSNode(const K& key, const T& val)
			:_key(key)
			, _val(val)
			,_left(nullptr)
			,_right(nullptr)
		{}
		K _key;
		T _val;
		BSNode<K, T>* _left;
		BSNode<K, T>* _right;//一定是指针，不是指针就错了
	};

	template<class K, class T>
	class BSTree {
		using node = BSNode<K,T>;
		//typedef BSNode<k, T> node;
	public:
		
		bool insert(const K& key,const T& val)
		{
			if (_root == nullptr)
			{
				//如果直接是空的，那么就直接插入
				_root = new node(key, val);
				return true;
			}
			node* parent = nullptr;
			node* cur = _root;
			while (cur)
			{
				if (key > cur->_key)
				{
					//大于就往右移：
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else {
					return false;
				}
			}
			cur = new node(key, val);
			if (key > parent->_key)
				parent->_right = cur;
			else
				parent->_left = cur;
			return true;
		}

		bool find(const K& key)
		{
			node* cur = _root;
			if (cur == nullptr)
			{
				return false;
			}
			while (cur)
			{
				if (key > cur->_key)
					cur = cur->_right;
				else if (key < cur->_key)
					cur = cur->_left;
				else {
					std::cout << cur->_key << " " << cur->_val << std::endl;
					return true;
				}
			}
			return false;
		}

		bool Erase(const K& key)
		{
			if (_root == nullptr)
				return false;//空无法删除就放回flase
			node* cur = _root;
			node* parent = nullptr;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else {
					//删除逻辑的具体实现：
					if (cur->_left == nullptr)
					{
						if (parent == nullptr)
							_root = _root->_right;
						else {
							if (cur == parent->_right)
								parent->_right = cur->_right;
							else
								parent->_left = cur->_right;
						}
						delete cur;
						return true;
					}
					else if (cur->_right == nullptr)
					{
						if (parent == nullptr)
							_root = _root->_left;
						else {
							if (cur == parent->_right)
								parent->_right = cur->_left;
							else
								parent->_left = cur->_left;
						}
						delete cur;
						return true;
					}
					else {
						//最复杂的：找到替换的R，完成替换
						node* replace = cur->_right;
						node* replaceParent = cur;
						while (replace->_left)
						{
							replaceParent = replace;
							replace = replace->_left;
						}
						cur->_key = replace->_key;
						//由于已经是最左边了，没有左子树，会带情况1：
						if (replace == replaceParent->_right)
							replaceParent->_right = replace->_right;
						else
							replaceParent->_left = replace->_right;
						delete replace;
						return true;
					}
				}
			}
			return false;
		}

		void InOrder()
		{
			_InOrder(_root);
		}


	private:
		void _InOrder(node* root)
		{
			if (root == nullptr)
				return;
			_InOrder(root->_left);
			std::cout << root->_key << ":" << root->_val << std::endl;
			_InOrder(root->_right);
		}

		node* _root = nullptr;
	};
}

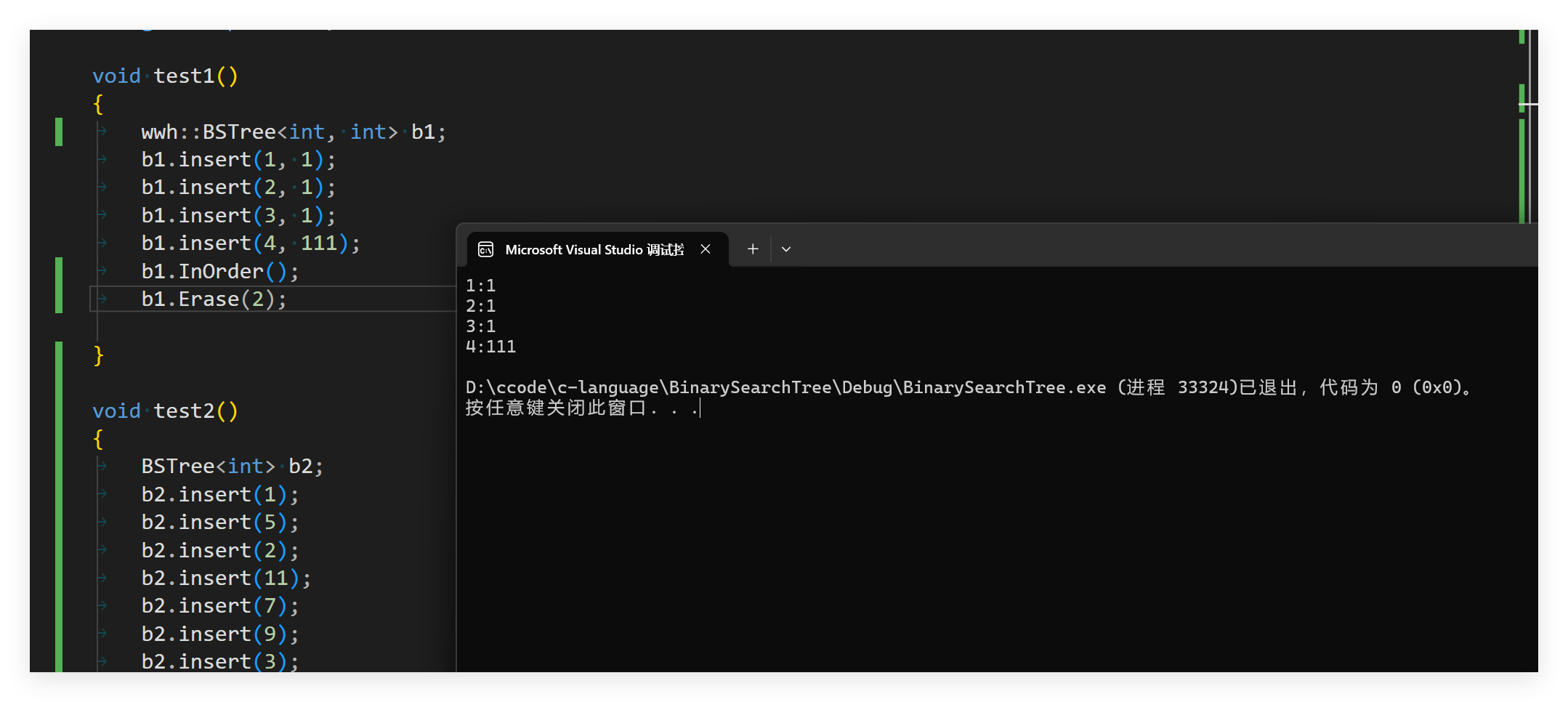
3. 总结：

二叉搜索树的学习是后面map和set的基础，也是未来后面的AVL树和红黑树的学习打上坚固的基础。希望这篇文章对你的学习有帮助。

相关推荐
小白程序员成长日记1 小时前
2025.12.01 力扣每日一题
算法·leetcode·职场和发展
Embedded-Xin1 小时前
Linux架构优化——spdlog实现压缩及异步写日志
android·linux·服务器·c++·架构·嵌入式
TL滕1 小时前
从0开始学算法——第四天（练点题吧）
数据结构·笔记·学习·算法
[J] 一坚1 小时前
华为OD、微软、Google、神州数码、腾讯、中兴、网易有道C/C++字符串、数组、链表、树等笔试真题精粹
c语言·数据结构·c++·算法·链表
我不会插花弄玉1 小时前
c++入门基础【由浅入深-C++】
c++
多则惑少则明1 小时前
【算法题4】找出字符串中的最长回文子串(Java版)
java·开发语言·数据结构·算法
不会编程的小寒1 小时前
C and C++
java·c语言·c++
迷途之人不知返1 小时前
二叉树题目
数据结构·算法
hewayou2 小时前
MFC +Com+ALT工程报 内存泄漏
c++·mfc·内存泄漏·com技术
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03BongoCat - 跨平台键盘猫动画工具04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05本地部署阿里最新开源的Z-Image06【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）07Linux下V2Ray安装配置指南08Meta第三代“分割一切”模型——SAM 3本地部署教程：首支持文本提示分割，400万概念、30毫秒响应，检测分割追踪一网打尽09Labelme从安装到标注：零基础完整指南10【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连