深度学习实战（基于pytroch）系列（四十）长短期记忆（LSTM）从零开始实现

长短期记忆（LSTM）

本节将介绍另一种常用的门控循环神经网络：长短期记忆（long short-term memory，LSTM）。它比上节我们讲的门控循环单元的结构稍微复杂一点。

长短期记忆

LSTM 中引入了3个门，即输入门（input gate）、遗忘门（forget gate）和输出门（output gate），以及与隐藏状态形状相同的记忆细胞（某些文献把记忆细胞当成一种特殊的隐藏状态），从而记录额外的信息。

输入门、遗忘门和输出门

与门控循环单元中的重置门和更新门一样，长短期记忆的门的输入均为当前时间步输入与上一时间步隐藏状态，输出由激活函数为sigmoid函数的全连接层计算得到。如此一来，这3个门元素的值域均为[0,1]。

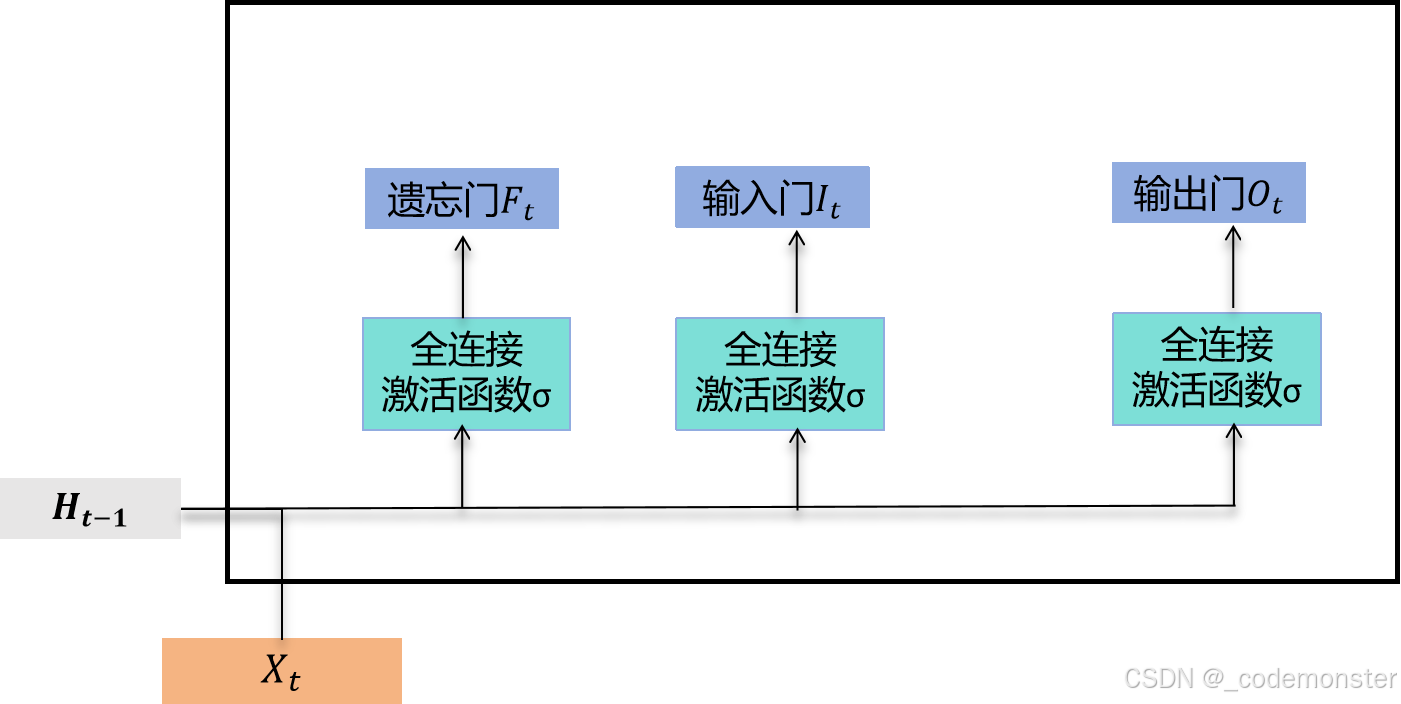
输入门、遗忘门和输出门的计算

具体来说，假设隐藏单元个数为 h，给定时间步 t 的小批量输入 X_t ∈ R^(n×d)（样本数为 n，输入个数为 d）和上一时间步隐藏状态 H_(t-1) ∈ R^(n×h)。时间步 t 的输入门 I_t、遗忘门 F_t 和输出门 O_t 分别计算如下：

I t = σ ( X t W x i + H ( t − 1 ) W h i + b i ) I_t = σ(X_t W_xi + H_(t-1) W_hi + b_i) It=σ(XtWxi+H(t−1)Whi+bi)
F t = σ ( X t W x f + H ( t − 1 ) W h f + b f ) F_t = σ(X_t W_xf + H_(t-1) W_hf + b_f) Ft=σ(XtWxf+H(t−1)Whf+bf)
O t = σ ( X t W x o + H ( t − 1 ) W h o + b o ) O_t = σ(X_t W_xo + H_(t-1) W_ho + b_o) Ot=σ(XtWxo+H(t−1)Who+bo)

其中的 W x i , W x f , W x o ∈ R ( d × h ) 和 W h i , W h f , W h o ∈ R ( h × h ) W_xi, W_xf, W_xo ∈ R^(d×h) 和 W_hi, W_hf, W_ho ∈ R^(h×h) Wxi,Wxf,Wxo∈R(d×h)和Whi,Whf,Who∈R(h×h) 是权重参数， b i , b f , b o ∈ R ( 1 × h ) b_i, b_f, b_o ∈ R^(1×h) bi,bf,bo∈R(1×h)是偏差参数。

候选记忆细胞

接下来，长短期记忆需要计算候选记忆细胞 C̃_t。它的计算与上面介绍的3个门类似，但使用了值域在[-1,1]的tanh函数作为激活函数。

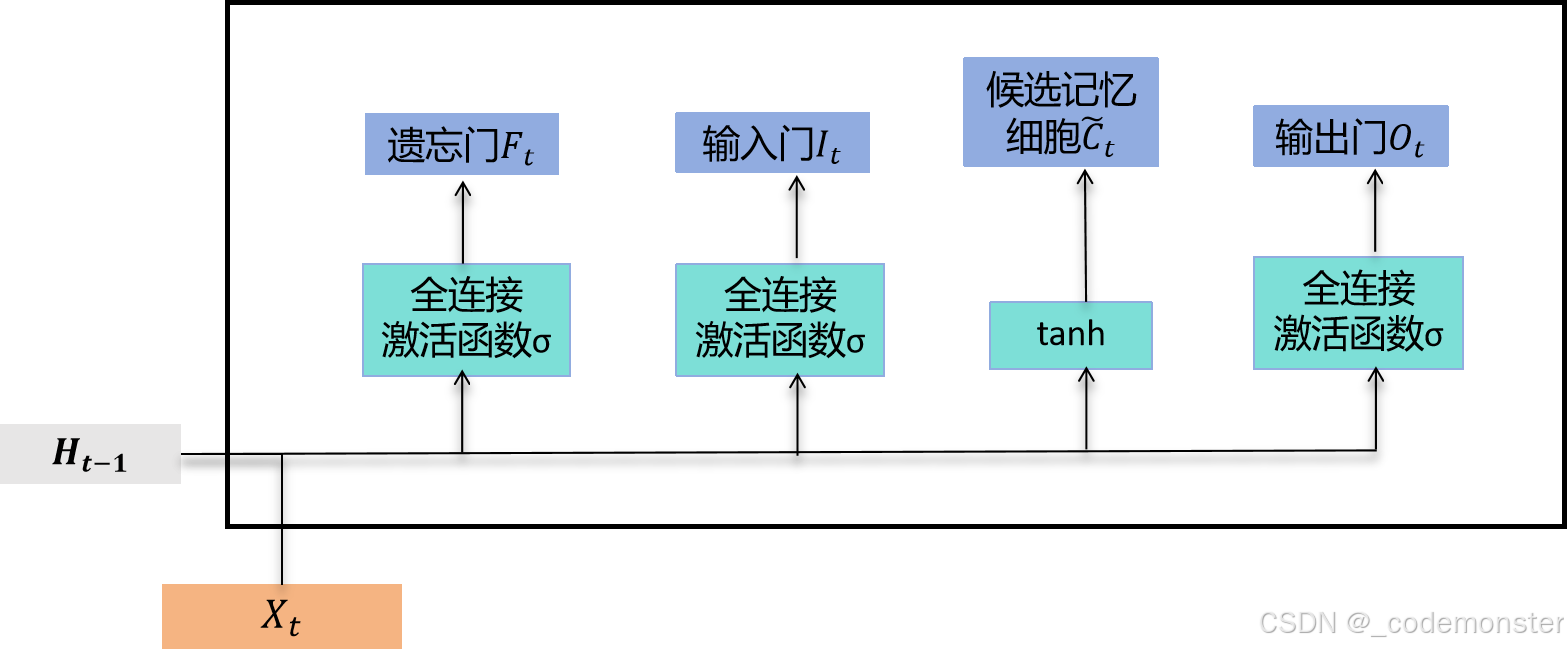
候选记忆细胞的计算

具体来说，时间步 t 的候选记忆细胞 C ~ t C̃_t C~t 的计算为

C ~ t = t a n h ( X t W x c + H ( t − 1 ) W h c + b c ) C̃_t = tanh(X_t W_xc + H_(t-1) W_hc + b_c) C~t=tanh(XtWxc+H(t−1)Whc+bc)

其中 W x c ∈ R ( d × h ) 和 W h c ∈ R ( h × h ) W_xc ∈ R^(d×h) 和 W_hc ∈ R^(h×h) Wxc∈R(d×h)和Whc∈R(h×h) 是权重参数， b c ∈ R ( 1 × h ) b_c ∈ R^(1×h) bc∈R(1×h) 是偏差参数。

记忆细胞

我们可以通过元素值域在[0,1]的输入门、遗忘门和输出门来控制隐藏状态中信息的流动，这一般也是通过使用按元素乘法（符号为 ⊙）来实现的。当前时间步记忆细胞 C_t 的计算组合了上一时间步记忆细胞和当前时间步候选记忆细胞的信息，并通过遗忘门和输入门来控制信息的流动：

C t = F t ⊙ C ( t − 1 ) + I t ⊙ C ~ t C_t = F_t ⊙ C_(t-1) + I_t ⊙ C̃_t Ct=Ft⊙C(t−1)+It⊙C~t

遗忘门控制上一时间步的记忆细胞 C ( t − 1 ) C_(t-1) C(t−1) 中的信息是否传递到当前时间步，而输入门则控制当前时间步的输入通过候选记忆细胞 C ~ t C̃_t C~t 如何流入当前时间步的记忆细胞。如果遗忘门一直近似1且输入门一直近似0，过去的记忆细胞将一直通过时间保存并传递至当前时间步。这个设计可以应对循环神经网络中的梯度衰减问题，并更好地捕捉时间序列中时间步距离较大的依赖关系。

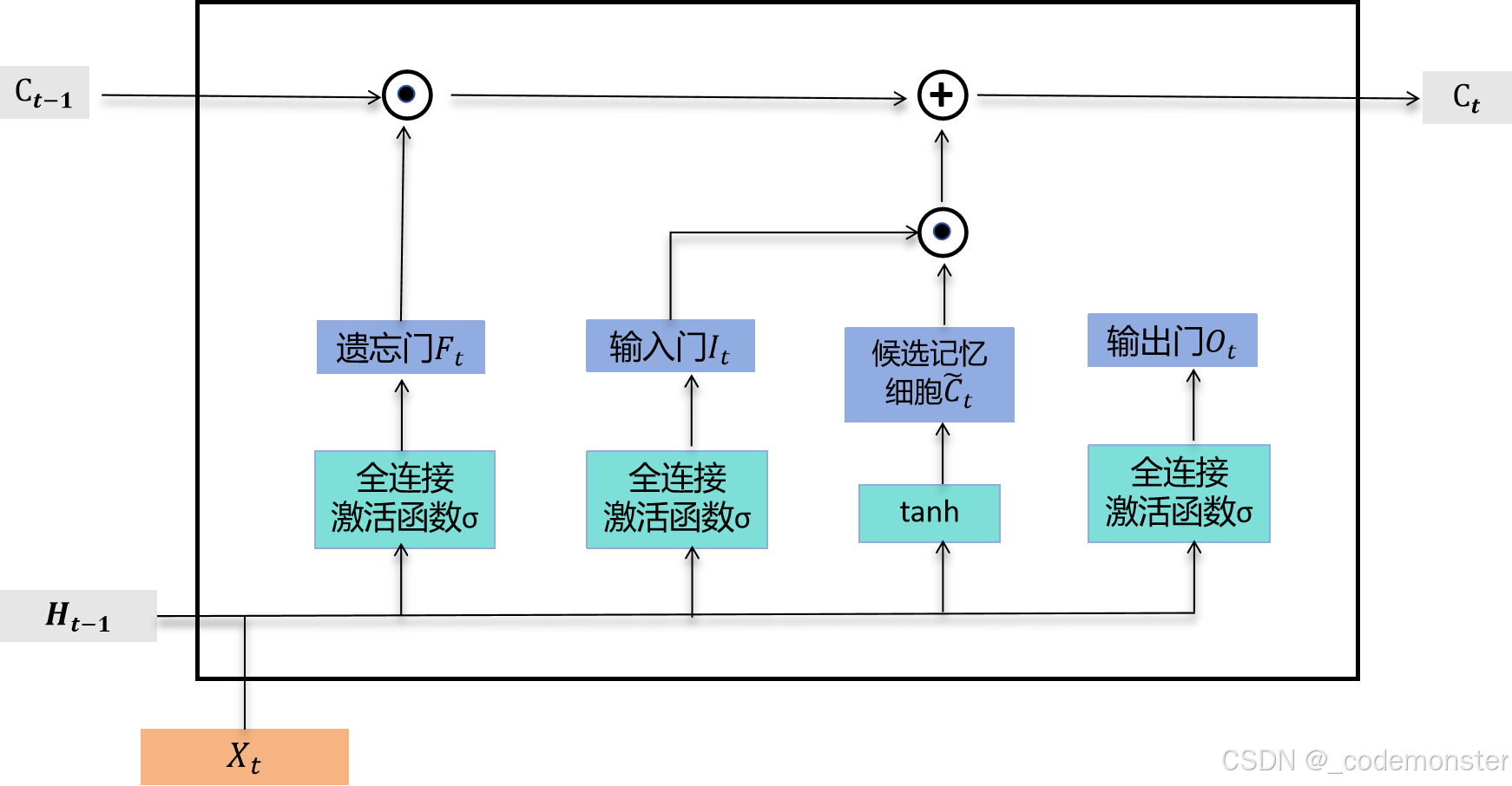
记忆细胞的计算。这里的⊙是按元素乘法

隐藏状态

有了记忆细胞以后，接下来我们还可以通过输出门来控制从记忆细胞到隐藏状态 H t H_t Ht 的信息的流动：

H t = O t ⊙ t a n h ( C t ) H_t = O_t ⊙ tanh(C_t) Ht=Ot⊙tanh(Ct)

这里的tanh函数确保隐藏状态元素值在-1到1之间。需要注意的是，当输出门近似1时，记忆细胞信息将传递到隐藏状态供输出层使用；当输出门近似0时，记忆细胞信息只自己保留。

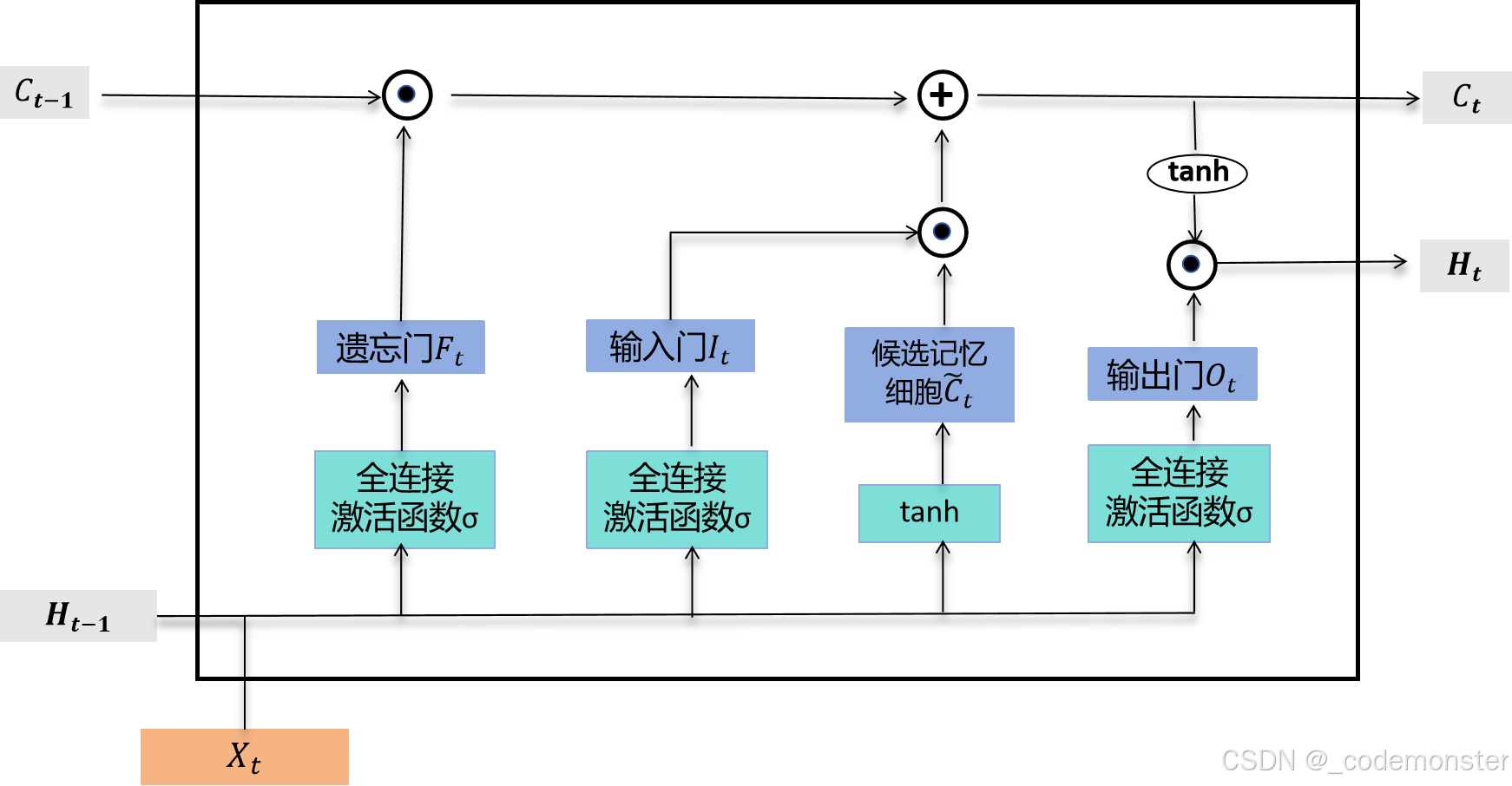
这里的⊙是按元素乘法

读取数据集

下面我们开始实现并展示长短期记忆。和前几节中的实验一样，这里依然使用周杰伦歌词数据集来训练模型作词。

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
import math
import random
import time
import zipfile

def load_data_jay_lyrics():
    with zipfile.ZipFile('../data/jaychou_lyrics.txt.zip') as zin:
        with zin.open('jaychou_lyrics.txt') as f:
            corpus_chars = f.read().decode('utf-8')
    corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')
    corpus_chars = corpus_chars[0:10000]
    idx_to_char = list(set(corpus_chars))
    char_to_idx = {char: i for i, char in enumerate(idx_to_char)}
    vocab_size = len(char_to_idx)
    corpus_indices = [char_to_idx[char] for char in corpus_chars]
    return corpus_indices, char_to_idx, idx_to_char, vocab_size


(corpus_indices, char_to_idx, idx_to_char, vocab_size) = load_data_jay_lyrics()

从零开始实现

我们先介绍如何从零开始实现长短期记忆。

初始化模型参数

下面的代码对模型参数进行初始化。超参数num_hiddens定义了隐藏单元的个数。

python 复制代码

def try_gpu():
    """If GPU is available, return torch.device('cuda'); else return torch.device('cpu')."""
    if torch.cuda.is_available():
        return torch.device('cuda')
    else:
        return torch.device('cpu')

num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
ctx = try_gpu()

def get_params():
    def _one(shape):
        return torch.randn(shape, device=ctx) * 0.01
    
    def _three():
        return (_one((num_inputs, num_hiddens)),
                _one((num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=ctx))
    
    W_xi, W_hi, b_i = _three()  # 输入门参数
    W_xf, W_hf, b_f = _three()  # 遗忘门参数
    W_xo, W_ho, b_o = _three()  # 输出门参数
    W_xc, W_hc, b_c = _three()  # 候选记忆细胞参数
    # 输出层参数
    W_hq = _one((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=ctx)
    # 附上梯度
    params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,
              b_c, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

定义模型

在初始化函数中，长短期记忆的隐藏状态需要返回额外的形状为(批量大小, 隐藏单元个数)的值为0的记忆细胞。

python 复制代码

def init_lstm_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device),
            torch.zeros((batch_size, num_hiddens), device=device))

下面根据长短期记忆的计算表达式定义模型。需要注意的是，只有隐藏状态会传递到输出层，而记忆细胞不参与输出层的计算。

python 复制代码

def lstm(inputs, state, params):
    [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
     W_hq, b_q] = params
    (H, C) = state
    outputs = []
    for X in inputs:
        I = torch.sigmoid(torch.matmul(X, W_xi) + torch.matmul(H, W_hi) + b_i)
        F = torch.sigmoid(torch.matmul(X, W_xf) + torch.matmul(H, W_hf) + b_f)
        O = torch.sigmoid(torch.matmul(X, W_xo) + torch.matmul(H, W_ho) + b_o)
        C_tilda = torch.tanh(torch.matmul(X, W_xc) + torch.matmul(H, W_hc) + b_c)
        C = F * C + I * C_tilda
        H = O * torch.tanh(C)
        Y = torch.matmul(H, W_hq) + b_q
        outputs.append(Y)
    return outputs, (H, C)

训练模型并创作歌词

同上一节一样，我们在训练模型时只使用相邻采样。设置好超参数后，我们将训练模型并根据前缀"分开"和"不分开"分别创作长度为50个字符的一段歌词。

python 复制代码

num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']

我们每过40个迭代周期便根据当前训练的模型创作一段歌词。

python 复制代码

def one_hot(x, n_class, dtype=torch.float32):
    # x shape: (batch_size,), 输出形状: (batch_size, n_class)
    x = x.long()
    res = torch.zeros(x.shape[0], n_class, dtype=dtype, device=x.device)
    res.scatter_(1, x.view(-1, 1), 1)
    return res


def to_onehot(X, n_class):
    # X shape: (batch_size, seq_len), 输出: seq_len个(batch_size, n_class)的Tensor
    return [one_hot(X[:, i], n_class) for i in range(X.shape[1])]


def grad_clipping(params, theta, device):
    norm = torch.tensor([0.0], device=device)
    for param in params:
        norm += (param.grad.data ** 2).sum()
    norm = norm.sqrt().item()
    if norm > theta:
        for param in params:
            param.grad.data *= (theta / norm)


def data_iter_random(corpus_indices, batch_size, num_steps, device=None):
    # 减1是因为输出的索引是相应输入的索引加1
    num_examples = (len(corpus_indices) - 1) // num_steps
    epoch_size = num_examples // batch_size
    example_indices = list(range(num_examples))
    random.shuffle(example_indices)
    
    # 返回从pos开始的长为num_steps的序列
    def _data(pos):
        return corpus_indices[pos: pos + num_steps]
    
    for i in range(epoch_size):
        # 每次读取batch_size个随机样本
        i = i * batch_size
        batch_indices = example_indices[i: i + batch_size]
        X = [_data(j * num_steps) for j in batch_indices]
        Y = [_data(j * num_steps + 1) for j in batch_indices]
        yield torch.tensor(X, device=device), torch.tensor(Y, device=device)

def data_iter_consecutive(corpus_indices, batch_size, num_steps, device=None):
    corpus_indices = torch.tensor(corpus_indices, device=device)
    data_len = len(corpus_indices)
    batch_len = data_len // batch_size
    indices = corpus_indices[0: batch_size * batch_len].reshape(
        batch_size, batch_len)
    epoch_size = (batch_len - 1) // num_steps
    for i in range(epoch_size):
        i = i * num_steps
        X = indices[:, i: i + num_steps]
        Y = indices[:, i + 1: i + num_steps + 1]
        yield X, Y

        
def predict_rnn(prefix, num_chars, rnn, params, init_rnn_state,
                num_hiddens, vocab_size, device, idx_to_char, char_to_idx):
    state = init_rnn_state(1, num_hiddens, device)
    output = [char_to_idx[prefix[0]]]
    for t in range(num_chars + len(prefix) - 1):
        # 将上一时间步的输出作为当前时间步的输入
        X = to_onehot(torch.tensor([[output[-1]]], device=device), vocab_size)
        # 计算输出和更新隐藏状态
        (Y, state) = rnn(X, state, params)
        # 下一个时间步的输入是prefix里的字符或者当前的最佳预测字符
        if t < len(prefix) - 1:
            output.append(char_to_idx[prefix[t + 1]])
        else:
            output.append(int(Y[0].argmax(dim=1).item()))
    return ''.join([idx_to_char[i] for i in output])


def train_and_predict_rnn(rnn, get_params, init_rnn_state, num_hiddens,
                          vocab_size, device, corpus_indices, idx_to_char,
                          char_to_idx, is_random_iter, num_epochs, num_steps,
                          lr, clipping_theta, batch_size, pred_period,
                          pred_len, prefixes):
    if is_random_iter:
        data_iter_fn = data_iter_random
    else:
        data_iter_fn = data_iter_consecutive
    params = get_params()
    loss = nn.CrossEntropyLoss()
    optimizer = optim.SGD(params, lr=lr)
    
    for epoch in range(num_epochs):
        if not is_random_iter:  # 如使用相邻采样，在epoch开始时初始化隐藏状态
            state = init_rnn_state(batch_size, num_hiddens, device)
        l_sum, n, start = 0.0, 0, time.time()
        data_iter = data_iter_fn(corpus_indices, batch_size, num_steps, device)
        for X, Y in data_iter:
            if is_random_iter:  # 如使用随机采样，在每个小批量更新前初始化隐藏状态
                state = init_rnn_state(batch_size, num_hiddens, device)
            else:  # 否则需要使用detach函数从计算图分离隐藏状态
                if isinstance(state, (tuple, list)):
                    for s in state:
                        s.detach_()
                else:
                    state.detach_()
            
            inputs = to_onehot(X, vocab_size)
            # outputs有num_steps个形状为(batch_size, vocab_size)的矩阵
            (outputs, state) = rnn(inputs, state, params)
            # 拼接之后形状为(num_steps * batch_size, vocab_size)
            outputs = torch.cat(outputs, dim=0)
            # Y的形状是(batch_size, num_steps)，转置后再变成长度为
            # batch * num_steps 的向量，这样跟输出的行一一对应
            y = Y.T.reshape(-1)
            
            # 使用交叉熵损失计算平均分类误差
            l = loss(outputs, y.long())
            
            optimizer.zero_grad()
            l.backward()
            grad_clipping(params, clipping_theta, device)  # 裁剪梯度
            optimizer.step()  # 因为误差已经取过均值，梯度不用再做平均
            l_sum += l.item() * y.numel()
            n += y.numel()
        
        if (epoch + 1) % pred_period == 0:
            print('epoch %d, perplexity %f, time %.2f sec' % (
                epoch + 1, math.exp(l_sum / n), time.time() - start))
            for prefix in prefixes:
                print(' -', predict_rnn(
                    prefix, pred_len, rnn, params, init_rnn_state,
                    num_hiddens, vocab_size, device, idx_to_char, char_to_idx))



train_and_predict_rnn(lstm, get_params, init_lstm_state, num_hiddens,
                          vocab_size, ctx, corpus_indices, idx_to_char,
                          char_to_idx, False, num_epochs, num_steps, lr,
                          clipping_theta, batch_size, pred_period, pred_len,
                          prefixes)

输出：

epoch 40, perplexity 211.715574, time 0.12 sec

分开我不不你我你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你

不分开我不不你我你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你你

epoch 80, perplexity 67.906983, time 0.11 sec

分开我想你这你我你不我想想我不要我不要我不要我不要我不要我不要我不要我不要我不要

不分开我想你这你我你不我想想我不要我不要我不要我不要我不要我不要我不要我不要我不要

epoch 120, perplexity 17.289810, time 0.12 sec

分开我想你的生笑我想想你你的我爱听别散你给我想你我想要你我不要你想你爱情了觉快知了

不分开我有你的生笑我想你的生笑像你你你的我有你你你的太笑像通你想我想你你我不了

epoch 160, perplexity 4.462036, time 0.11 sec

分开我已了其实怎我想就这样说对怎么我想是这样我的手空是给是用你么开么我想就没想我的没

不分开我有你分小我我想就这样牵你你开开觉又过了一个秋后知后觉我该好好生活我该好好生活不知

小结

长短期记忆的隐藏层输出包括隐藏状态和记忆细胞。只有隐藏状态会传递到输出层。
长短期记忆的输入门、遗忘门和输出门可以控制信息的流动。
长短期记忆可以应对循环神经网络中的梯度衰减问题，并更好地捕捉时间序列中时间步距离较大的依赖关系。

本系列目录链接