二叉树的层序遍历
题目描述
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
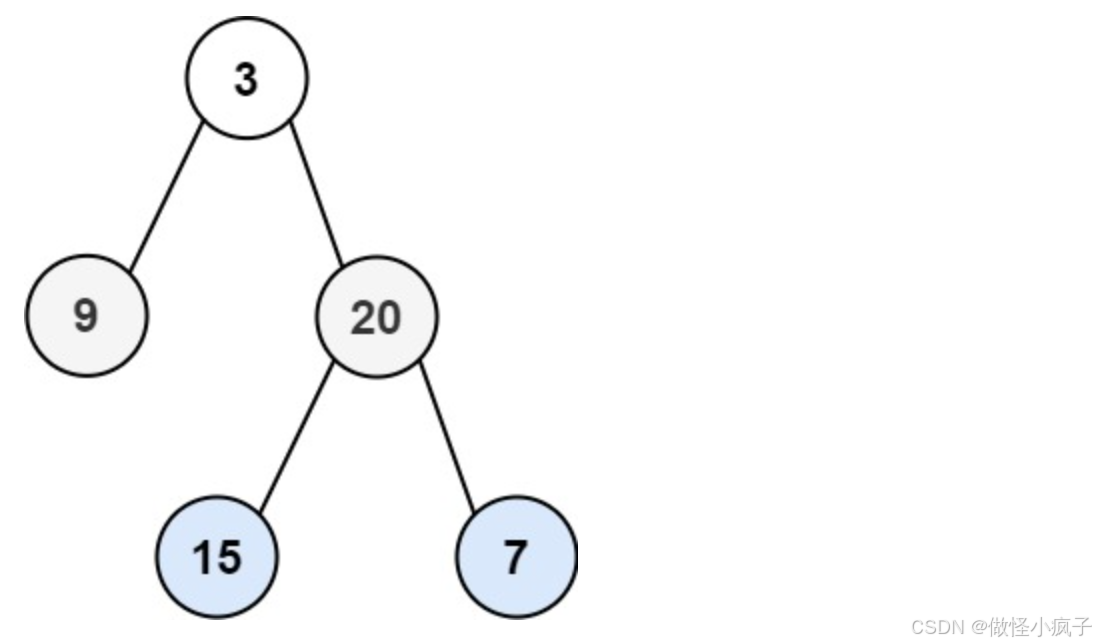
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
求解
一开始直接把节点 push 到ans中了,就报错了,应该是把相关节点放进去。
js
var levelOrder = function(root) {
if (!root) return [];
let ans = [];
let queue = [root];
while (queue.length !== 0) {
const levelSize = queue.length; // 当前层的节点数
let temp = []; // 存节点的值,不是节点
for (let i= 0; i < levelSize; i++) {
let node = queue.shift();
temp.push(node.val);
if (node.left) queue.push(node.left);
if (node.right) queue.push(node.right)
}
ans.push(temp);
}
return ans;
};将有序数组转换为二叉搜索树
题目描述
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。
示例 1:
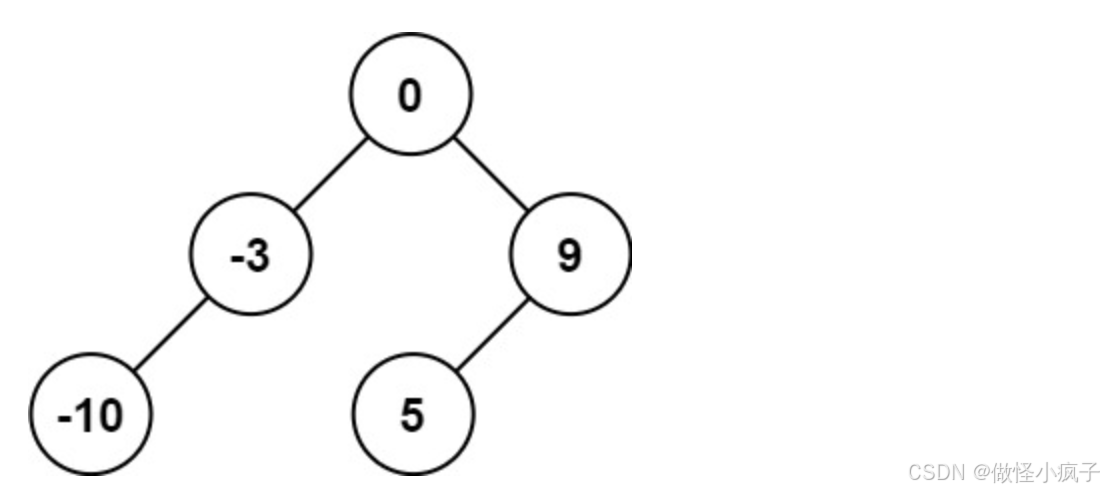
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
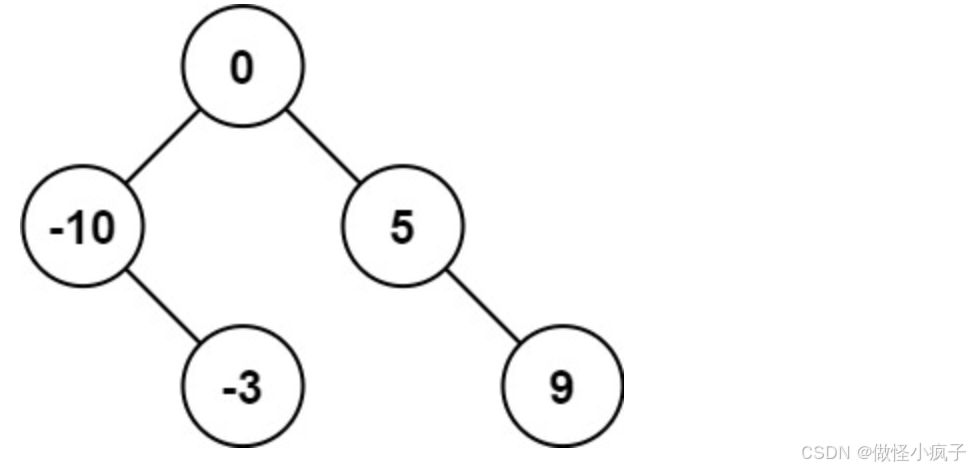
示例 2:
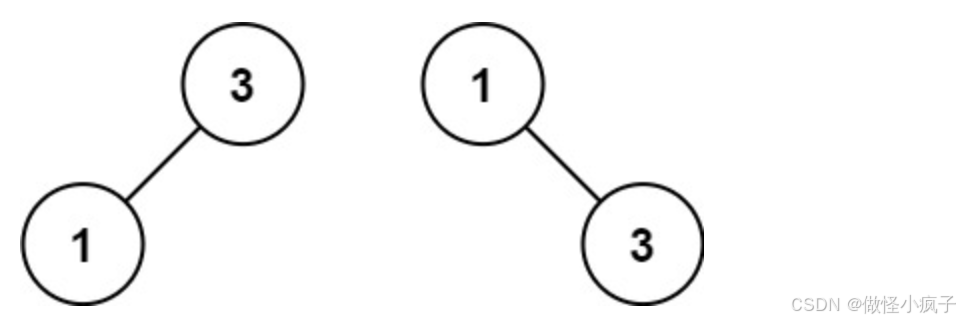
输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按 严格递增 顺序排列
求解
1. 二叉搜索树(BST)是什么?
二叉搜索树(Binary Search Tree,简称 BST),也叫二叉排序树,是一种满足特定规则的二叉树结构,核心特点是便于快速查找、插入、删除操作(平均时间复杂度为 O (logn))。
2. 二叉搜索树的核心规律(性质)
节点值的大小关系:
-
左子树中所有节点的值都小于当前节点的值;
-
右子树中所有节点的值都大于当前节点的值;
-
每个子树本身也必须是一棵二叉搜索树(递归满足上述规则)。
示例:
plaintext
5
/ \
3 7
/ \ / \
2 4 6 8- 节点 5 的左子树(3、2、4)都小于 5,右子树(7、6、8)都大于 5;节点 3 的左子树(2)小于 3,右子树(4)大于 3,以此类推。
- 中序遍历的特性对二叉搜索树进行中序遍历(左→根→右),得到的结果是严格升序的序列。比如上面的例子,中序遍历结果为:2 → 3 → 4 → 5 → 6 → 7 → 8,这是 BST 最关键的特性之一。
- 唯一性(可选)若树中不允许重复值,则任意节点的左右子树值不会等于自身;若允许重复,通常约定重复值放在右子树(或左子树)。
3. 有序数组转二叉搜索树的思路
因为有序数组本身是 BST 的中序遍历结果,要转成 BST,需保证树的平衡性(避免退化成链表),通常采用二分法:
- 取数组中间元素作为根节点(保证左右子树高度差≤1);
- 左半部分数组递归构建左子树;
- 右半部分数组递归构建右子树。
代码:
js
var sortBST = function(nums, head, tail) {
if (head > tail) return null;
let mid = (head + tail) >> 1; // 选择中间位置左边的数字作为根节点
// let mid = (head + tail + 1) >> 1; // 选择中间位置右边的数字作为根节点
let root = new ListNode(nums[mid]);
root.left = sortBST(nums, head, mid - 1);
root.right = sortBST(nums, mid + 1, tail);
return root;
};
var sortedArrayToBST = function(nums) {
// 二分
return sortBST(nums, 0, nums.length - 1)
};