之前涉及机器学习问题的时候,有很多评估指标 那么到底选谁作为主指标很困难(或者说不严谨),这时候我们需要一个客观公正的教练,他可以根据值的分布自行判断谁是最优的。
之前我们介绍了多目标优化-帕累托最优点的思想,他解决的是没有任何指标能在不损害其他指标的前提下更优,筛选非支配解
今天我们来介绍下评价问题,他是专门为这类问题而生的。最主流的方法就是熵权法+TOPSIS,我们来介绍下这个方法。
- **指标的冲突性:**不同的评估指标(如准确率、召回率、F1-Score、AUC等)往往是相互冲突的。一个模型可能在召回率上很高,但在准确率上较差
- 主观性风险: 如果采用人为赋权,权重完全依赖于专家的经验和判断,容易引入人为偏差,难以做到客观公正,
- **缺乏统一标准:**传统的指标筛选(如只看 F1-Score)过于片面,无法对所有指标进行整体的、科学的权衡。
熵权法(Entropy Weight Method): 一种客观赋权法 。它根据指标数据的离散程度(变异性)来确定权重。信息量越大(数据波动越大),权重越高;信息量越小(数据越一致),权重越低。
TOPSIS (Technique for Order Preference by Similarity to ldeal Solution): 一种多目标决策分析方法 。它通过计算每个待评价对象(如不同模型)与理想解 和负理想解 的距离,来确定其相对优劣,从而得到一个科学的排序。
整个方法论可以分为两大阶段:第一阶段:客观赋权(权法) ;第二阶段:综合评价与排序(TOPSIS)。
有很多思路都可以排序:
1.对规范归一化后的矩阵直接指标加和排序
2.每一个模型到理想点的距离(越小越好)
3.每一个模型到负理想点的距离(越大越好)
4.topsis考虑的越多,考虑到了+-理想点的距离
通过TOPSIS结合熵权法,我们成功地:
- 客观赋权:避免了主观判断,让数据(准确率、召回率、训练时间)的波动性决定了它们在评估中的重要程度。
2.综合排序:得到了一个基于所有加权指标的值,该值公正地衡量了每个模型与完美模型(理想解)的相似程度。
是否不用熵权,直接用 TOPSIS 也可以?
TOPSIS 的核心是"距离排序",而熵权法只是用来解决"权重怎么定"的一个插件。可以把熵权法拔掉,换成别的。
1.主观:人为确定权重,但是主观方法亦有差距,有的主观方法更加客观,ahp层次分析法
2.等权重法:不处理
所以熵权法只是赋权的一种方法,可选甚至可以不用。他算是评价问题中重要的环。
评价问题真正核心的是他的评价算法,有三个经典的算法:
- topsis
- **层次分析法(AHP):**主观评价,通过问卷构成判断矩阵,需要满足一致性检验
- **灰色关联度分析法 GRA:**基于几何形状问题,适合小样本
但是核心都是殊途同归,我们一般在机器学习中只会用我今天介绍的这套组合
一、定义指标方向与数据预处理
机器不懂"时间越短越好,准确率越高越好",我们需要手动告诉它哪些是效益型(越大越好),哪些是成本型(越小越好)。同时,为了避免后续计算ln(0)出错,我们需要做一个极小值处理。
python
# --- 模块一:准备工作 ---
# 1. 区分指标类型
# 效益型指标 (越大越好):准确率、召回率、F1、AUC
benefit_cols = ['Accuracy', 'Recall', 'F1-Score', 'AUC']
# 成本型指标 (越小越好):训练时间
cost_cols = ['Training Time (s)']
# 2. 复制一份数据用于计算,保留原始数据用于展示
data_eval = results_df.copy()
# 3. 数据类型转换(确保是浮点数,方便计算)
data_eval = data_eval.astype(float)
print("步骤 1 完成:指标方向已定义。")
print(f"效益型指标 (+): {benefit_cols}")
print(f"成本型指标 (-): {cost_cols}")
二、数据标准化(Normalization)
消除量纲影响。时间的单位是"秒",准确率是"百分比",如果不标准化,数值大的指标(如时间可能是100多)会主导权重计算。我们使用最常用的Min-Max标准化。
python
# --- 模块二:数据标准化 ---
# 为了避免 log(0) 出现,我们加一个极小的数 epsilon
epsilon = 1e-6
# 1. 处理效益型指标 (x - min) / (max - min)
for col in benefit_cols: # 遍历每一个效益型指标列,找到该列的最小值和最大值
min_val = data_eval[col].min()
max_val = data_eval[col].max()
# 如果最大值等于最小值(所有模型表现一样),则设为 1 或 0,防止除以 0
if max_val == min_val:
data_eval[col] = 1.0
else:
data_eval[col] = (data_eval[col] - min_val) / (max_val - min_val)
# 2. 处理成本型指标 (max - x) / (max - min)
for col in cost_cols: # 遍历每一个成本型指标列,找到该列的最小值和最大值
min_val = data_eval[col].min()
max_val = data_eval[col].max()
if max_val == min_val:
data_eval[col] = 1.0
else:
data_eval[col] = (max_val - data_eval[col]) / (max_val - min_val)
# 3. 加上 epsilon 防止后续 log(0) 报错
data_eval = data_eval + epsilon
print("\n步骤 2 完成:数据已标准化(消除了量纲差异)。")
print(data_eval.head())三、熵权法计算权重(Entropy Weights)
利用信息熵原理,计算数据的离散程度。逻辑:数据越分散👉信息量越大👉熵值越小👉权重越高。潜台词:大家都会做的题(指标差异小),不能用来拉开分差(权重低)。
python
# --- 模块三:熵权法计算权重 ---
n, m = data_eval.shape # n是模型数量,m是指标数量
# 1. 计算比重 P_ij
# 即:某模型在某指标下的数值 占 该指标所有模型数值之和 的比例
P = data_eval.div(data_eval.sum(axis=0), axis=1)
# 2. 计算信息熵 E_j
# k 是常数,与样本数 n 有关:k = 1 / ln(n)
k = 1 / np.log(n)
E = -k * (P * np.log(P)).sum(axis=0)
# 3. 计算信息冗余度 d_j
d = 1 - E
# 4. 计算最终权重 w_j
weights = d / d.sum()
# 展示权重结果
weights_df = pd.DataFrame(weights, columns=['Weight']).sort_values(by='Weight', ascending=False)
print(weights_df)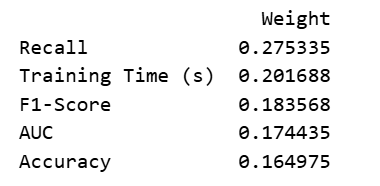
权重越大的指标,说明各模型在该指标上的表现差异越大,对排名的影响也越大。
四、TOPSIS综合评价
- 加权:把刚才算出的权重乘进去
- 找标杆:找出每一列最好的值(理想解)和最差的值(负理想解)
- 算距离:你的模型离"完美"有多远?离"最差"有多远?
- 打分:相对接近度
python
# --- 模块四:TOPSIS 计算与排序 ---
# 1. 构建加权规范化矩阵 V
# 将标准化后的数据 乘以 对应的权重
V = data_eval * weights
# 2. 确定正理想解 (V+) 和 负理想解 (V-)
# 因为我们在模块二已经做过方向处理(成本型转为了效益型),
# 所以这里统一:最大值就是理想解,最小值就是负理想解
V_plus = V.max()
V_minus = V.min()
# 3. 计算欧氏距离
# D+ : 每个模型 与 理想解 的距离
D_plus = np.sqrt(((V - V_plus) ** 2).sum(axis=1))
# D- : 每个模型 与 负理想解 的距离
D_minus = np.sqrt(((V - V_minus) ** 2).sum(axis=1))
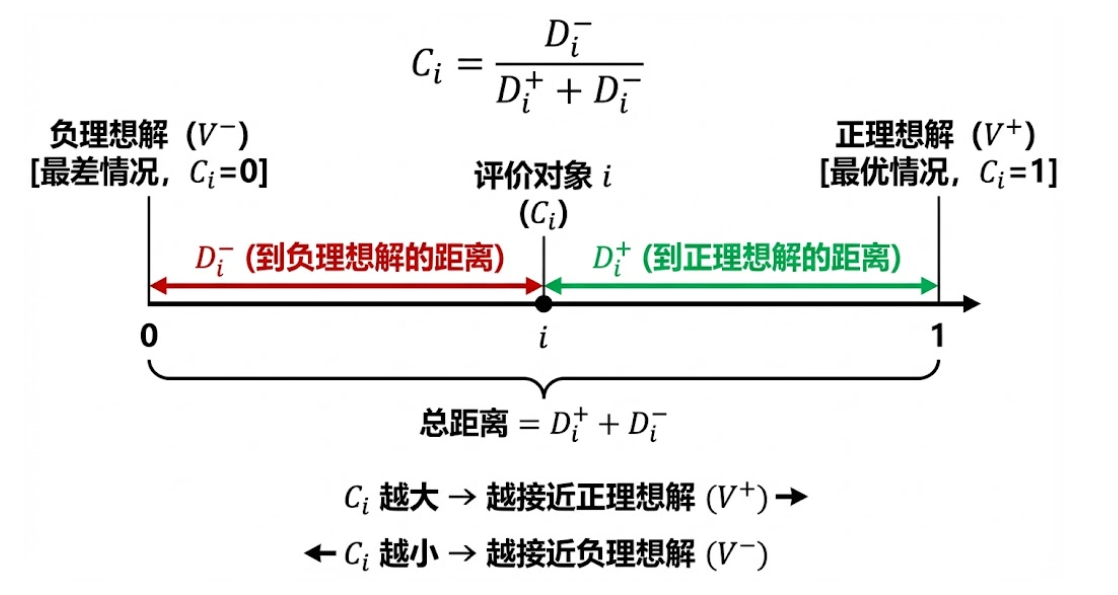
# 4. 计算相对接近度 C_i (最终得分)
# Score = D- / (D+ + D-)
# Score 越接近 1,说明离负理想解越远,离理想解越近 -> 越好
scores = D_minus / (D_plus + D_minus)
# 5. 整理最终结果
final_results = results_df.copy() # 拿回原始数据方便展示
final_results['TOPSIS Score'] = scores
final_results['Rank'] = final_results['TOPSIS Score'].rank(ascending=False).astype(int)
# 按排名排序
final_results = final_results.sort_values(by='Rank')
print("\n步骤 4 完成:最终 TOPSIS 评估排名:")
print(final_results[['Accuracy', 'Recall', 'Training Time (s)', 'TOPSIS Score', 'Rank']])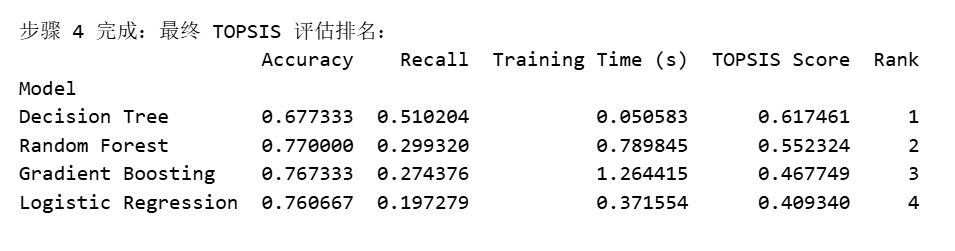
**作业:**对于之前提到的回归问题应用该方法实现
python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
import warnings
warnings.filterwarnings('ignore')
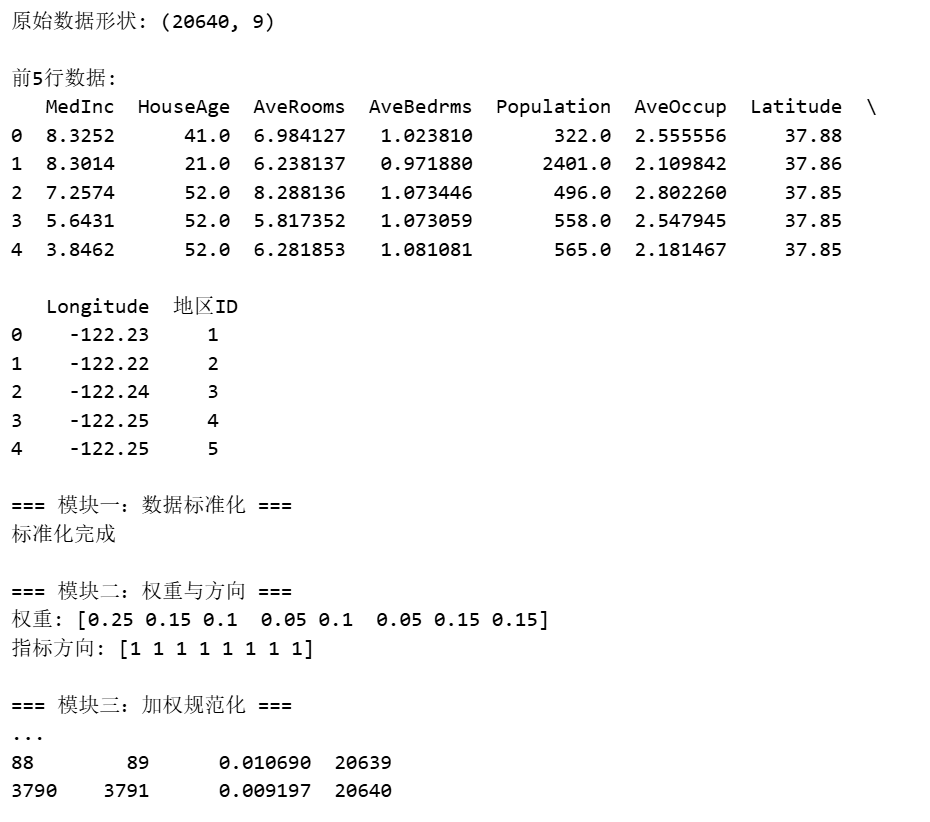
# --- 1. 加载数据 ---
california = fetch_california_housing()
df = pd.DataFrame(california.data, columns=california.feature_names)
df['地区ID'] = range(1, len(df) + 1)
print("原始数据形状:", df.shape)
print("\n前5行数据:")
print(df.head())
# --- 模块一:数据标准化 ---
print("\n=== 模块一:数据标准化 ===")
# 提取特征数据(排除地区ID)
data = df.iloc[:, :-1].values
# 标准化(向量归一化)
norm_data = data / np.sqrt(np.sum(data**2, axis=0))
print("标准化完成")
# --- 模块二:权重设置与方向处理 ---
print("\n=== 模块二:权重与方向 ===")
# 定义权重(可根据需要调整)
weights = np.array([0.25, 0.15, 0.10, 0.05, 0.10, 0.05, 0.15, 0.15])
# 定义指标方向:+1为效益型,-1为成本型
# 实际应用中,经度纬度需要特殊处理,这里简化为效益型
impacts = np.array([1, 1, 1, 1, 1, 1, 1, 1])
# 方向处理:如果是成本型指标,取倒数
for i in range(len(impacts)):
if impacts[i] == -1: # 成本型
norm_data[:, i] = 1 / norm_data[:, i]
print(f"权重: {weights}")
print(f"指标方向: {impacts}")
# --- 模块三:构建加权规范化矩阵 ---
print("\n=== 模块三:加权规范化 ===")
# 构建加权规范化矩阵 V
V = norm_data * weights
print("加权规范化矩阵V的形状:", V.shape)
# --- 模块四:TOPSIS 计算与排序 ---
print("\n=== 模块四:TOPSIS 计算与排序 ===")
# 1. 确定正理想解 (V+) 和 负理想解 (V-)
V_plus = V.max(axis=0) # 每列最大值
V_minus = V.min(axis=0) # 每列最小值
# 2. 计算欧氏距离
D_plus = np.sqrt(((V - V_plus) ** 2).sum(axis=1)) # 与理想解的距离
D_minus = np.sqrt(((V - V_minus) ** 2).sum(axis=1)) # 与负理想解的距离
# 3. 计算相对接近度 C_i (最终得分)
scores = D_minus / (D_plus + D_minus)
# 4. 整理最终结果
results = pd.DataFrame({
'地区ID': df['地区ID'].values,
'TOPSIS_Score': scores
})
# 添加排名
results['Rank'] = results['TOPSIS_Score'].rank(ascending=False).astype(int)
results = results.sort_values(by='Rank')
print("\nTOPSIS评估结果(前20名):")
print(results.head(20))
print("\nTOPSIS评估结果(后20名):")
print(results.tail(20))
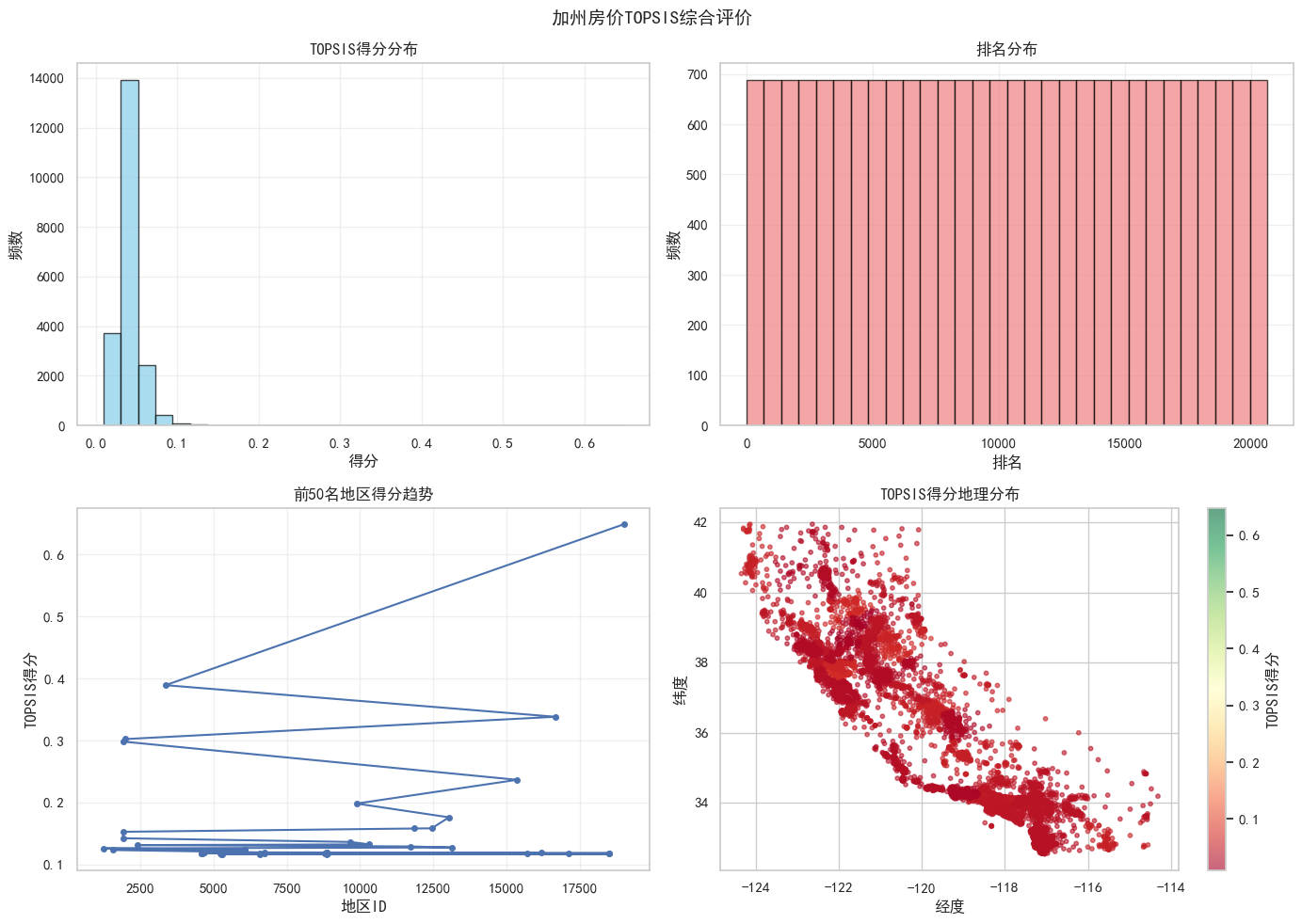
# --- 可视化 ---
print("\n=== 结果可视化 ===")
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
# 1. 得分分布
axes[0, 0].hist(results['TOPSIS_Score'], bins=30, color='skyblue', edgecolor='black', alpha=0.7)
axes[0, 0].set_title('TOPSIS得分分布')
axes[0, 0].set_xlabel('得分')
axes[0, 0].set_ylabel('频数')
axes[0, 0].grid(True, alpha=0.3)
# 2. 排名分布
axes[0, 1].hist(results['Rank'], bins=30, color='lightcoral', edgecolor='black', alpha=0.7)
axes[0, 1].set_title('排名分布')
axes[0, 1].set_xlabel('排名')
axes[0, 1].set_ylabel('频数')
axes[0, 1].grid(True, alpha=0.3)
# 3. 前50名得分趋势
top_50 = results.head(50)
axes[1, 0].plot(top_50['地区ID'], top_50['TOPSIS_Score'], 'b-o', markersize=4)
axes[1, 0].set_title('前50名地区得分趋势')
axes[1, 0].set_xlabel('地区ID')
axes[1, 0].set_ylabel('TOPSIS得分')
axes[1, 0].grid(True, alpha=0.3)
# 4. 地理分布
scatter = axes[1, 1].scatter(df['Longitude'], df['Latitude'],
c=results['TOPSIS_Score'], cmap='RdYlGn',
s=10, alpha=0.6)
axes[1, 1].set_title('TOPSIS得分地理分布')
axes[1, 1].set_xlabel('经度')
axes[1, 1].set_ylabel('纬度')
plt.colorbar(scatter, ax=axes[1, 1], label='TOPSIS得分')
plt.suptitle('加州房价TOPSIS综合评价', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.show()
# --- 结果分析 ---
print("\n=== 结果分析 ===")
print(f"得分统计:")
print(f"最小值: {results['TOPSIS_Score'].min():.4f}")
print(f"平均值: {results['TOPSIS_Score'].mean():.4f}")
print(f"中位数: {results['TOPSIS_Score'].median():.4f}")
print(f"最大值: {results['TOPSIS_Score'].max():.4f}")
print(f"标准差: {results['TOPSIS_Score'].std():.4f}")
# 得分等级划分
results['等级'] = pd.qcut(results['TOPSIS_Score'],
q=4,
labels=['差', '中下', '中上', '优'])
print(f"\n地区等级分布:")
print(results['等级'].value_counts().sort_index())
print(f"\n最优地区 (ID: {results.iloc[0]['地区ID']}):")
print(f" 得分: {results.iloc[0]['TOPSIS_Score']:.4f}")
print(f" 排名: {results.iloc[0]['Rank']}")
print(f"\n最差地区 (ID: {results.iloc[-1]['地区ID']}):")
print(f" 得分: {results.iloc[-1]['TOPSIS_Score']:.4f}")
print(f" 排名: {results.iloc[-1]['Rank']}")
# 保存结果
results.to_csv('california_topsis_results.csv', index=False, encoding='utf-8-sig')
print(f"\n结果已保存到: california_topsis_results.csv")