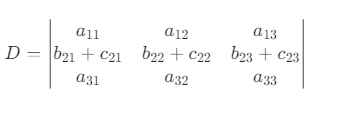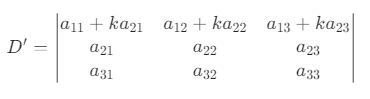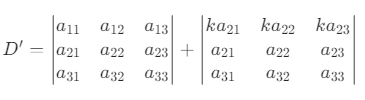转置行列式
把上面行列式按照主对角线翻转后结果如下，使用来表示：
转置后，在转置
性质一：
行列地位相同，对行性质，队列性质
证明：
现有一个上三角行列式如下
转置后为下三角行列式
所以
性质二：
用k乘以D的某一行元素，等于用k乘以D
证明：
如下有一个4阶行列式，结果是主对角线相乘
将第一行元素都乘以 k，第一行第一列为1，其他项目均为0，则行列式如下：
所以
如果有n行都乘以k，则
性质三：
交换两行(列)行列式，D值符号改变
证明：
如下有一个3阶行列式，按行展开，依据列标排列统计逆序数，1后面为0，2后面为0，3后面为0， 则逆序数为0+0+0
第一行和第二行交换，按行展开，依据列标排列统计逆序数，2后面为1，1后面为0，3后面为0， 则逆序数为1+0+0
所以
性质四：
D的某一行为两数之和，则表示成两个行列式的和。
证明：
现有三阶行列式，第二行为第一列为
, 第二行第二列为
根据三阶行列式，展开结果如下：
将每一项拆分为含
上述两部分分别对应两个三阶行列式 D1 和 D2：
因此，
性质五：
将行列式的某一行（列），乘以一个数k加到另一行，行列式的值不变
证明：
构造三阶行列式D
将 D 的第 2 行乘以 k 加到第 1 行，得到新行列式 D′：
根据 "某一行是两数之和的行列式可拆分为两个行列式的和"，将 D′ 拆分为 D1+D2
观察 D2，其第 1 行是第 2 行的 k 倍（两行成比例）。根据行列式性质："若行列式有两行（列）成比例，则行列式值为 0，因此 D2=0。
结合上述结果，D′=D+0=D，即 "将行列式某一行乘以数 k 加到另一行，行列式值不变"
对称行列式
若行列式 D 满足 转置等于自身 （即），则称 D 为对称行列式。
，转置后
，且元素满足 a12=a21=2、a13=a31=3 等。
若行列式 D 满足 转置等于自身 （即 DT=D），则称 D 为对称行列式。
从元素角度看：对称行列式的元素满足 aij=aji（i,j 为任意行、列下标）。
反对称行列式：
若行列式 D 满足 转置等于自身的相反数 （即 ），则称 D 为反对称行列式。
从元素角度看：反对称行列式的元素满足
，转置后
，且主对角线元素均为 0，满足
奇数阶反对称行列式值为 0：
若 D 是 n 阶反对称行列式（n 为奇数），则
偶数阶反对称行列式值为完全平方数：