前言:很久没有更新博客了,大概在4月份就没有更新了,那时候忙着实习,后面忙着比赛,还要处理班级事务(班长),没有太多时间更新,就断更了,现在会慢慢更新的,拾起前面断更的内容,同时也会写一下力扣周赛比较难的题,或者蓝桥杯难的算法题!谢谢大家支持!
题目:
给你一个二维整数数组 points,其中 points[i] = [xi, yi] 表示第 i 个点在笛卡尔平面上的坐标。
返回可以从 points 中任意选择四个不同点组成的梯形的数量。
梯形 是一种凸四边形,具有 至少一对平行边。两条直线平行当且仅当它们的斜率相同。
示例 1:
输入: points = [[-3,2],[3,0],[2,3],[3,2],[2,-3]]
输出: 2
解释:
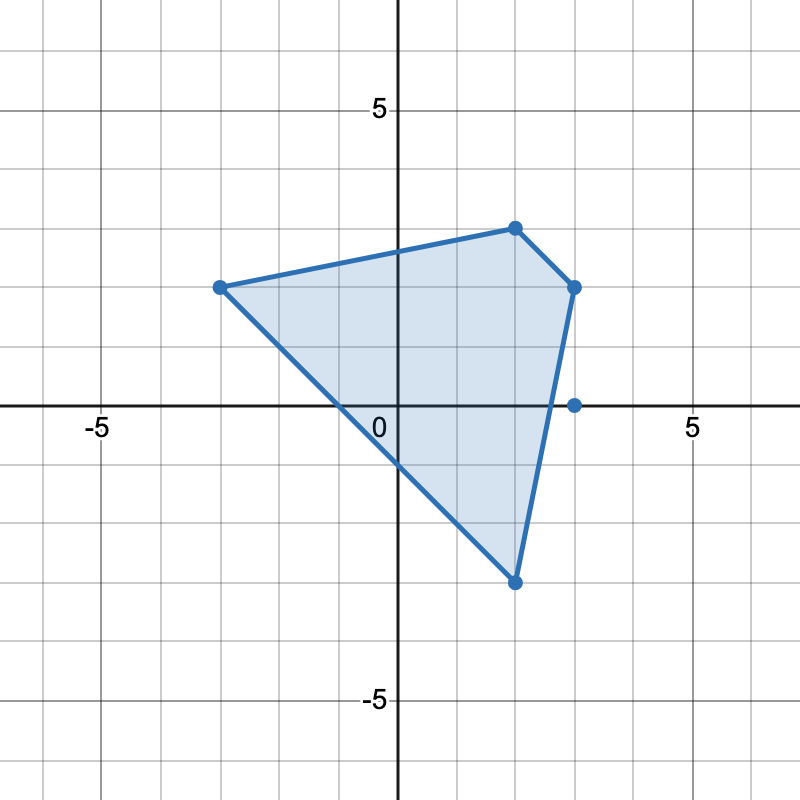
有两种不同方式选择四个点组成一个梯形:
- 点
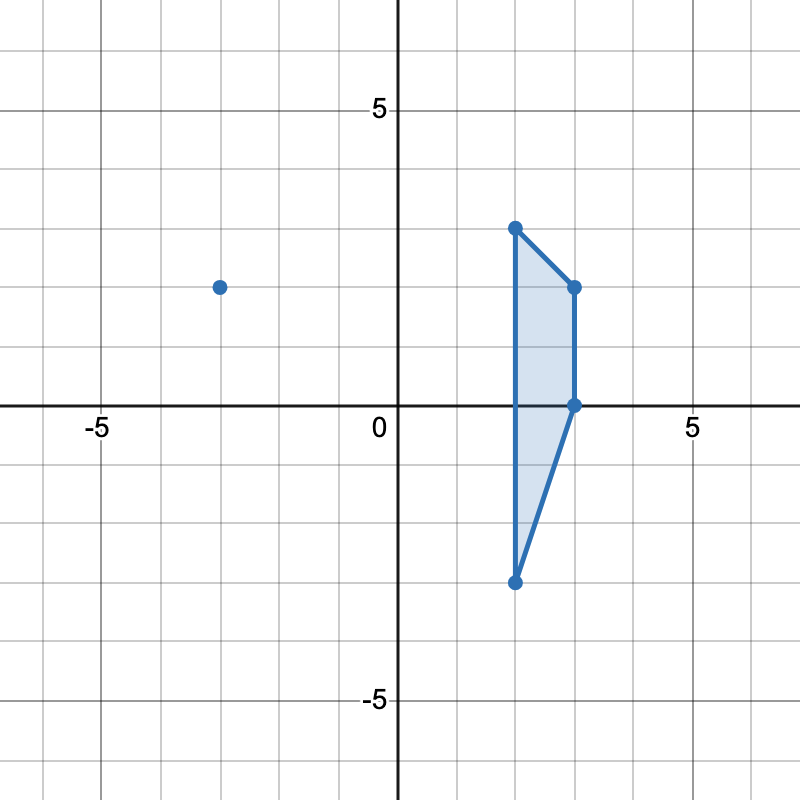
[-3,2], [2,3], [3,2], [2,-3]组成一个梯形。 - 点
[2,3], [3,2], [3,0], [2,-3]组成另一个梯形。
示例 2:
输入: points = [[0,0],[1,0],[0,1],[2,1]]
输出: 1
解释:
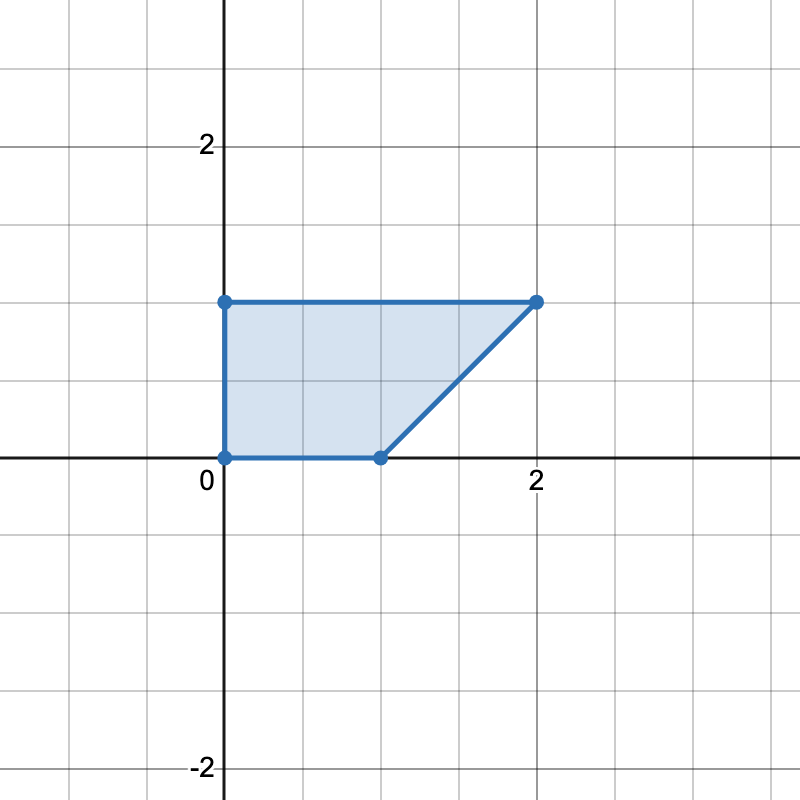
只有一种方式可以组成一个梯形。
提示:
4 <= points.length <= 500--1000 <= xi, yi <= 1000- 所有点两两不同。
与3623. 统计梯形的数目 I不同,但是想法差不多。
题目分析:
第一步:这个题和3623. 统计梯形的数目 I不一样,但是首先肯定可以想到一个斜率,按斜率来分类线段,但是这里有一个问题,就是可能会选同一个斜率,但是共线,这显然不能构成梯形,所有再次引入一个截距b,就是与y轴的交点,这样可以排除同斜率共线的情况,所以定义哈希表时,需要再嵌套一个哈希表,把斜率k,截距b,和这样的线段个数,记录一下。
第二步:线段我们找出来了,然后算总数还是和3623. 统计梯形的数目 I一样的,这里可以参考 灵神(灵茶山艾府)的 枚举右,维护左 的思想,但是这里有一个问题,因为我们按斜率和截距来统计的,所以如果构成的是平行四边形,是计算了两次,因为有两条平行线,所以如果是平行四边形,数量就得减1,但是再判断是不是平行四边形,这里又需要想一下,用平行四边形的特征,两对角线的中点重合,即mid,然后是同一个斜率k,再求个数,所有这里还需要定义哈希表,需要再嵌套一个哈希表,把斜mid,截距k,和这样个数。记录一下。
题目分析完了,就来看代码怎么写。
代码(Java)附注释:
class Solution {
public int countTrapezoids(int[][] points) {
Map<Double,Map<Double,Integer>> cnt = new HashMap<>();
Map<Integer,Map<Double,Integer>> cnt2 = new HashMap<>();
int n = points.length;
for(int i = 0;i<n;i++){
int x = points[i][0],y = points[i][1];
for(int j = 0;j<i;j++){
int x2 = points[j][0],y2 = points[j][1];
int dy = y - y2;
int dx = x - x2;
double k = dx != 0 ? 1.0 * dy / dx : Double.MAX_VALUE;
double b = dx != 0 ? 1.0 * (y*dx - dy*x)/dx : x;
if(k == -0.0){
k = 0.0;
}
if(b == -0.0){
b = 0.0;
}
cnt.computeIfAbsent(k,_ -> new HashMap<>()).merge(b,1,Integer::sum);
int mid = (x + x2 + 2000) * 10000 + (y + y2 + 2000);
cnt2.computeIfAbsent(mid,_ -> new HashMap<>()).merge(k,1,Integer::sum);
}
}
int ans = 0;
for(Map<Double,Integer> m : cnt.values()){
int s = 0;
for(int c : m.values()){
ans += s * c;
s += c;
}
}
for(Map<Double,Integer> m :cnt2.values()){
int s = 0;
for(int c : m.values()){
ans -= s * c;
s += c;
}
}
return ans;
}
}
解析(附图片):
1、哈希表定义
//定义哈希表cnt 斜率 -> 截距 -> 个数
Map<Double,Map<Double,Integer>> cnt = new HashMap<>();
//定义哈希表cnt2 中点 -> 斜率 -> 个数
Map<Integer,Map<Double,Integer>> cnt2 = new HashMap<>();
2、统计斜率和截距,中点和对应的个数
int n = points.length;//数组长度
for(int i = 0;i<n;i++){
int x = points[i][0],y = points[i][1];//点1
for(int j = 0;j<i;j++){
int x2 = points[j][0],y2 = points[j][1];//点2
int dy = y - y2;
int dx = x - x2;
//斜率,三目运算符,不说,dx等于0,就是垂直x轴,这个时候斜率是无穷大,
//其余情况就是两点式计算斜率,此时截距就以x为标识
double k = dx != 0 ? 1.0 * dy / dx : Double.MAX_VALUE;
double b = dx != 0 ? 1.0 * (y*dx - dy*x)/dx : x;
// 归一化 把- 0.0 转换为 0.0
//这里是因为哈希表会把这两个作为不同的值记录
//但实则是同一个,只是点 谁前谁后的问题
if(k == -0.0){
k = 0.0;
}
if(b == -0.0){
b = 0.0;
}
//存值
cnt.computeIfAbsent(k,_ -> new HashMap<>()).merge(b,1,Integer::sum);
//中点计算
int mid = (x + x2 + 2000) * 10000 + (y + y2 + 2000);
//存值
cnt2.computeIfAbsent(mid,_ -> new HashMap<>()).merge(k,1,Integer::sum);
}
}
3、哈希表存值这里细说一下
两个存值的过程是Java 8+ 中非常简洁高效 的写法,用于在嵌套 Map(即 Map<K, Map<V, Integer>>)中安全地累加计数。
第一步:cnt.computeIfAbsent(k, _ -> new HashMap<>())
- 如果
cnt中不存在 keyk,就执行new HashMap<>(),并把结果存入cnt[k] - 如果已存在 ,就直接返回
cnt.get(k) - 返回值是一个
Map<Double, Integer>(即内层 map)
✅ 这避免了手动判断
if (!cnt.containsKey(k)) cnt.put(k, new HashMap<>());
第二步:.merge(b, 1, Integer::sum)
对上一步返回的内层 map 执行:
- 如果
b不存在 ,就插入b → 1 - 如果
b已存在 ,就执行oldValue + 1(因为Integer::sum等价于(a, b) -> a + b)
✅ 这等价于:
map.put(b, map.getOrDefault(b, 0) + 1);,但更函数式、更安全
为什么加 2000?
题目中坐标范围是:
−1000≤x,y≤1000
那么:
x + x2的范围是:-2000到2000y + y2同理
但数组下标或哈希 key 不能为负数,所以我们加上偏移量 2000,将其映射到非负区间:
| 原始值 | 加 2000 后 |
|---|---|
| -2000 | 0 |
| 0 | 2000 |
| 2000 | 4000 |
现在 sumX + 2000 ∈ [0, 4000],共 4001 种可能。
为什么乘以 10000?
我们要把二维坐标 (a, b) 压缩成一个整数,且保证不冲突(唯一性)。
常用方法是:
key=a×M+b
其中 M 必须 大于 b 的最大可能值。
这里:
a = x + x2 + 2000 ∈ [0, 4000]b = y + y2 + 2000 ∈ [0, 4000]
所以只要 M > 4000,就不会冲突。
我选了 M = 10000(足够大,且是整万,便于阅读)。
⚠️ 注意:这不是真正的"中点",而是"两倍中点"的偏移编码
//存值
cnt.computeIfAbsent(k,_ -> new HashMap<>()).merge(b,1,Integer::sum);
//中点计算
int mid = (x + x2 + 2000) * 10000 + (y + y2 + 2000);
//存值
cnt2.computeIfAbsent(mid,_ -> new HashMap<>()).merge(k,1,Integer::sum);
4、计数逻辑详解
第一步:统计所有"斜率相同"的线段对
- 对每个斜率
k,遍历其所有截距组(即不同直线)。 s是之前所有直线上的线段总数。s * c表示:当前直线上的 c 条线段,与之前所有非共线(不同 b)的线段配对。- ✅ 这正好统计了所有不共线的平行线段对!
为什么?因为共线的线段在同一
(k,b)组内,而这里c是按b分开的,所以s和c来自不同直线 → 不共线 → 能构成梯形!
🎉 所以这一步的结果就是:所有梯形数量(包括平行四边形)。
第二步:减去多算的平行四边形
- 对每个中点
mid,遍历其所有斜率组。 s * c表示:中点相同、斜率相同的线段对数量。- 而"中点相同 + 平行" ⇨ 这两条线段是对边,构成平行四边形。
但平行四边形有两对平行边 ,所以在第一步中被算了 2 次 !
而我们只需要算 1 次 ,所以要 减去 1 次。
因此,ans -= 平行四边形数量,最终结果正确。
再 return 返回结果。
int ans = 0;
for(Map<Double,Integer> m : cnt.values()){
int s = 0;
for(int c : m.values()){
ans += s * c;
s += c;
}
}
for(Map<Double,Integer> m :cnt2.values()){
int s = 0;
for(int c : m.values()){
ans -= s * c;
s += c;
}
}
结语:这是力扣周赛一道有难度的算法题,可能没有思路或者没有想清楚,当时有部分人没有写出来或答案不对,思考出现偏差,希望看完之后可以解决你的困惑!一什么问题可以私信或者评论讨论丶,同时有问题或者改进的欢迎指出!