文章目录
- 一、K-Means聚类相关理论
-
- [1. K-Means聚类的核心定义](#1. K-Means聚类的核心定义)
- [2. K-Means聚类的底层核心原理](#2. K-Means聚类的底层核心原理)
-
- [2.1 目标函数:误差平方和(SSE)](#2.1 目标函数:误差平方和(SSE))
- [2.2 核心逻辑:迭代优化的贪心策略](#2.2 核心逻辑:迭代优化的贪心策略)
- [2.3 距离度量的选择逻辑](#2.3 距离度量的选择逻辑)
- [3. K-Means聚类的完整算法流程](#3. K-Means聚类的完整算法流程)
- [4. K-Means聚类的关键问题与解决方案](#4. K-Means聚类的关键问题与解决方案)
-
- [4.1 问题1:如何确定最优簇数K?](#4.1 问题1:如何确定最优簇数K?)
-
- [方法1:肘部法则(Elbow Method)](#方法1:肘部法则(Elbow Method))
- [方法2:轮廓系数(Silhouette Coefficient)](#方法2:轮廓系数(Silhouette Coefficient))
- 方法3:业务场景约束
- [4.2 问题2:初始簇中心如何优化?](#4.2 问题2:初始簇中心如何优化?)
- [4.3 问题3:对异常值敏感如何解决?](#4.3 问题3:对异常值敏感如何解决?)
- [4.4 问题4:不适用于非球形簇如何解决?](#4.4 问题4:不适用于非球形簇如何解决?)
- [5. K-Means聚类的特性与适用场景](#5. K-Means聚类的特性与适用场景)
-
- [5.1 核心特性](#5.1 核心特性)
- [5.2 适用场景](#5.2 适用场景)
- [6. 总结](#6. 总结)
- 二、scikit-learn中k-means聚类相关方法介绍
-
- [1. k-means聚类构造方法](#1. k-means聚类构造方法)
-
- [1.1 方法签名及参数解释](#1.1 方法签名及参数解释)
- [1.2 参数取值说明](#1.2 参数取值说明)
- [2. k-means聚类构造方法返回对象的方法](#2. k-means聚类构造方法返回对象的方法)
- [3. k-means聚类构造方法返回对象的属性](#3. k-means聚类构造方法返回对象的属性)
- [4. k-means聚类模型评估指标](#4. k-means聚类模型评估指标)
- 三、pandas.DataFrame中的绘图方法
-
- [1. 绘图方法介绍](#1. 绘图方法介绍)
- [2. 参数介绍](#2. 参数介绍)
-
- [2.1 图表类型与数据映射参数](#2.1 图表类型与数据映射参数)
- [2.2 图表样式与标签参数](#2.2 图表样式与标签参数)
- [2.3 布局与显示参数](#2.3 布局与显示参数)
- [2.4 特定图表专属参数](#2.4 特定图表专属参数)
- [3. 使用示例](#3. 使用示例)
- 四、基于K-Means的鸢尾花数据聚类分析
-
- [1. 数据挖掘目标](#1. 数据挖掘目标)
- [2. 数据收集与加载](#2. 数据收集与加载)
-
- [2.1 数据集介绍](#2.1 数据集介绍)
- [2.2 数据加载](#2.2 数据加载)
- [3. 探索性数据分析](#3. 探索性数据分析)
-
- [3.1 数据基本信息](#3.1 数据基本信息)
- [3.2 单特征分布分析](#3.2 单特征分布分析)
- [3.2 特征间相关性分析](#3.2 特征间相关性分析)
- [3.3 变异系数分析](#3.3 变异系数分析)
- [4. 数据预处理](#4. 数据预处理)
-
- [4.1 异常值检测与处理](#4.1 异常值检测与处理)
- [4.2 特征标准化](#4.2 特征标准化)
- [5. 模型构建(模型选择、训练)](#5. 模型构建(模型选择、训练))
-
- [5.1 确定最优聚类数k](#5.1 确定最优聚类数k)
- [5.2 K-Means聚类模型构建](#5.2 K-Means聚类模型构建)
- [6. 模型评估](#6. 模型评估)
-
- [6.1 核心评估指标](#6.1 核心评估指标)
- [6.2 聚类结果可视化](#6.2 聚类结果可视化)
-
- [6.2.1 聚类标签分布可视化](#6.2.1 聚类标签分布可视化)
- [6.2.2 聚类效果可视化](#6.2.2 聚类效果可视化)
- [6.2.3 原始尺度的簇中心可视化](#6.2.3 原始尺度的簇中心可视化)
- [6.2.4 标准化后的簇中心可视化](#6.2.4 标准化后的簇中心可视化)
- 五、完整代码
-
- [1. 完整代码](#1. 完整代码)
一、K-Means聚类相关理论
在无监督学习领域,聚类算法是挖掘数据内在结构与隐藏规律的核心工具,而K-Means聚类以其简单直观、高效可扩展的特性,成为工业界和学术界应用最广泛的聚类算法之一。无论是用户画像细分、商品推荐分组,还是图像分割、异常检测,K-Means都能以较低的计算成本快速输出有价值的聚类结果。本文将从核心定义、底层原理、算法流程、关键问题及优化方向等维度,系统梳理K-Means聚类的相关理论,为后续实践应用奠定基础。
1. K-Means聚类的核心定义
K-Means聚类是一种基于"距离度量"的划分式聚类算法,其核心目标是:将给定的N个样本数据,按照特征相似度划分为K个互不重叠的子集(称为"簇",Cluster),使得每个子集中的样本都具有较高的相似度,而不同子集间的样本相似度较低。
从定义中可提炼出K-Means的三个核心要素:
-
预设簇数K:K是算法的输入参数,需由用户根据业务场景或数据特性预先设定,这也是"K-Means"中"K"的由来。例如,在电商用户细分中,若需将用户划分为"高价值""中价值""低价值"三类,则K取值为3。
-
相似度度量:K-Means以"距离"衡量样本间的相似度,距离越小,相似度越高。最常用的距离度量是欧几里得距离(Euclidean Distance),适用于连续型特征数据;此外,也可根据数据类型选择曼哈顿距离(Manhattan Distance)、余弦相似度(Cosine Similarity)等。
-
簇中心(Centroid):每个簇的"代表",是该簇内所有样本特征的均值向量(又称"质心")。K-Means通过迭代更新簇中心,不断优化样本的簇划分结果,最终使簇内样本围绕簇中心聚集。
简单来说,K-Means的本质是"围绕簇中心的样本聚集"------通过反复调整簇中心的位置和样本的簇归属,最终实现"簇内紧凑、簇间分散"的聚类效果。
2. K-Means聚类的底层核心原理
K-Means的聚类过程本质是一个"目标函数优化 "的迭代过程,其底层原理围绕"误差平方和(Sum of Squared Errors, SSE)最小化"展开,通过贪心策略逐步逼近最优聚类结果。
2.1 目标函数:误差平方和(SSE)
K-Means以"簇内样本到其簇中心的距离平方和之和"作为目标函数,称为误差平方和(SSE),其计算公式为:
S S E = Σ (簇 = 1 到 K ) Σ (样本 ∈ 簇) ∣ ∣ x i − μ c ∣ ∣ 2 SSE = Σ(簇=1到K)Σ(样本∈簇)||x_i - μ_c||² SSE=Σ(簇=1到K)Σ(样本∈簇)∣∣xi−μc∣∣2
其中, x i x_i xi是簇c内的第i个样本, μ c μ_c μc是簇c的中心向量, ∣ ∣ ⋅ ∣ ∣ ||·|| ∣∣⋅∣∣表示欧几里得距离。
目标函数SSE的物理意义是"所有样本到其簇中心的整体偏离程度",K-Means的核心任务就是通过迭代优化,找到使SSE最小的K个簇划分方案。SSE越小,说明簇内样本的聚集程度越高,聚类效果越好。
2.2 核心逻辑:迭代优化的贪心策略
K-Means通过"分配-更新"的迭代过程最小化SSE,这是一种典型的贪心策略------每一步迭代都朝着使SSE降低的方向调整,最终收敛到局部最优解。其核心逻辑可拆解为两个关键步骤:
-
样本分配(簇归属更新):在簇中心固定的情况下,将每个样本分配到距离其最近的簇中心所在的簇。这一步通过最小化单个样本到簇中心的距离,直接降低整体SSE。
-
簇中心更新:在样本簇归属固定的情况下,重新计算每个簇的中心向量(即簇内所有样本特征的均值)。由于簇中心是簇内样本的"平均位置",这一步能进一步拉近簇内样本与簇中心的距离,从而降低SSE。
这两个步骤交替进行,直到SSE的下降幅度小于预设阈值(如0.001),或迭代次数达到上限,算法停止并输出最终聚类结果。需要注意的是,K-Means的贪心策略只能保证收敛到局部最优解,而非全局最优解,其最终结果会受初始簇中心选择的影响。
2.3 距离度量的选择逻辑
距离度量直接影响K-Means的聚类效果,需根据数据的特征类型和业务场景合理选择,常见的距离度量及适用场景如下:
-
欧氏距离 :最常用的距离度量,计算公式为 ∣ ∣ x i − x j ∣ ∣ = √ [ Σ ( d = 1 到 D ) ( x i d − x j d ) 2 ] ||x_i - x_j|| = √[Σ(d=1到D)(x_id - x_jd)²] ∣∣xi−xj∣∣=√[Σ(d=1到D)(xid−xjd)2](D为特征维度)。适用于连续型特征数据,且特征量纲一致(如身高、体重等经过标准化后的特征)。
-
曼哈顿距离 :又称"城市街区距离",计算公式为 ∣ ∣ x i − x j ∣ ∣ = Σ ( d = 1 到 D ) ∣ x i d − x j d ∣ ||x_i - x_j|| = Σ(d=1到D)|x_id - x_jd| ∣∣xi−xj∣∣=Σ(d=1到D)∣xid−xjd∣。适用于特征维度多、且关注"绝对差异"的场景(如文本中词频的差异),对异常值的敏感度低于欧几里得距离。
-
余弦相似度 :衡量两个向量的夹角余弦值,取值范围为[-1,1],值越接近1,相似度越高。计算公式为 c o s θ = ( x i ⋅ x j ) / ( ∣ ∣ x i ∣ ∣ ⋅ ∣ ∣ x j ∣ ∣ ) cosθ = (x_i·x_j) / (||x_i||·||x_j||) cosθ=(xi⋅xj)/(∣∣xi∣∣⋅∣∣xj∣∣)。适用于高维稀疏数据(如文本向量、图像特征),关注样本的"方向一致性"而非"数值大小",例如判断两篇文章的主题相似度。
需要特别注意的是,若特征量纲差异较大(如"年龄"范围为0-100,"收入"范围为0-100000),直接使用欧几里得距离会导致"收入"特征的权重被过度放大,因此在聚类前需对特征进行标准化(Standardization)或归一化(Normalization)处理。
3. K-Means聚类的完整算法流程
K-Means的算法流程简洁清晰,核心围绕"初始化簇中心→迭代优化→收敛停止"三个阶段展开,具体步骤如下:
步骤1:数据预处理与参数设置
-
数据清洗:处理原始数据中的缺失值(如用均值/中位数填充)、异常值(如通过箱线图剔除),确保数据质量。
-
特征标准化/归一化 :若特征量纲不一致,对每个特征进行标准化 x ′ = ( x − μ ) / σ x' = (x - μ)/σ x′=(x−μ)/σ 或归一化 x ′ = ( x − m i n ) / ( m a x − m i n ) x' = (x - min)/(max - min) x′=(x−min)/(max−min),消除量纲影响。
-
设置参数:预设簇数K、最大迭代次数(如100次)、收敛阈值(如SSE下降幅度小于1e-4时停止)。
步骤2:初始化K个簇中心
从N个样本中随机选择K个不重复的样本作为初始簇中心。这一步是K-Means的关键------若初始簇中心选择不当(如过于集中),可能导致算法收敛到较差的局部最优解,或迭代次数大幅增加。为优化初始簇中心选择,后续衍生出了K-Means++算法(将在1.5节介绍)。
步骤3:迭代优化(分配-更新)
这是K-Means的核心阶段,通过交替执行"样本分配"和"簇中心更新"两个步骤,逐步降低SSE,具体如下:
子步骤3.1:样本分配(簇归属更新)
对每个样本 x i x_i xi,计算其到K个簇中心的距离(如欧几里得距离),将$x_i¥分配到距离最近的簇中心对应的簇中,更新所有样本的簇归属标签。
子步骤3.2:簇中心更新
对每个簇c,计算该簇内所有样本的特征均值向量,将其作为新的簇中心 μ c μ_c μc,替代原有的簇中心。若某一簇内无样本(极端情况),可重新随机选择一个样本作为该簇的中心。
子步骤3.3:判断收敛条件
计算当前迭代的SSE,并与上一次迭代的SSE进行对比:
-
若SSE的下降幅度小于预设阈值,或簇中心的变化量小于阈值,说明算法已收敛,停止迭代。
-
若未收敛,且迭代次数未达到上限,返回子步骤3.1继续迭代;若达到最大迭代次数仍未收敛,也停止迭代并输出结果。
步骤4:输出聚类结果与评估
算法停止后,输出最终的K个簇划分结果(每个样本的簇归属标签)、各簇的中心向量及最终的SSE值。同时,通过聚类评估指标(如轮廓系数、CH指数)验证聚类效果,若效果不佳,可调整K值或距离度量方式重新执行算法。
4. K-Means聚类的关键问题与解决方案
K-Means虽简单高效,但在实际应用中存在诸多关键问题,如K值难以确定、初始簇中心影响结果、对异常值敏感等。针对这些问题,业界已形成成熟的解决方案,是用好K-Means的核心。
4.1 问题1:如何确定最优簇数K?
K是K-Means的核心参数,但数据本身的"真实簇数"往往未知,盲目设置K值会导致聚类效果偏差。常用的K值确定方法包括:
方法1:肘部法则(Elbow Method)
核心逻辑:随着K值的增加,簇内样本的聚集程度提高,SSE会不断下降;但当K超过数据的真实簇数后,SSE的下降幅度会显著减缓,形成一个"肘部"(Elbow),肘部对应的K值即为最优簇数。
操作步骤:设置K的取值范围(如1到10),对每个K值运行K-Means并计算SSE,以K为横轴、SSE为纵轴绘制折线图,找到折线由陡变缓的"肘部"对应的K值。例如,当K=3时SSE为1000,K=4时SSE为980(下降幅度仅2%),而K=2到K=3时SSE从2000降至1000(下降幅度50%),则K=3为最优值。
方法2:轮廓系数(Silhouette Coefficient)
核心逻辑:从"样本自身的聚类合理性"出发,衡量每个样本的"轮廓系数",所有样本的平均轮廓系数越大,聚类效果越好,对应的K值越优。
轮廓系数的计算逻辑:对样本 x i x_i xi, a i a_i ai是其与簇内其他所有样本的平均距离(簇内相似度), b i b_i bi是其与距离最近的其他簇内所有样本的平均距离(簇间相似度),则 x i x_i xi的轮廓系数为 s i = ( b i − a i ) / m a x ( a i , b i ) s_i = (b_i - a_i)/max(a_i, b_i) si=(bi−ai)/max(ai,bi)。 s i s_i si的取值范围为 [ − 1 , 1 ] [-1,1] [−1,1], s i s_i si越接近1,说明样本聚类越合理;越接近-1,说明样本更适合划分到其他簇。
方法3:业务场景约束
在实际业务中,K值可由业务需求直接确定。例如,电商平台需将商品划分为"热销""平销""滞销"三类,则K=3;金融机构需将客户风险等级划分为"高风险""中风险""低风险",则K=3。这种方法优先满足业务需求,再通过聚类评估指标验证合理性。
4.2 问题2:初始簇中心如何优化?
传统K-Means随机选择初始簇中心,易导致收敛到局部最优解。K-Means++算法通过"距离加权"的方式优化初始簇中心选择,核心思想是"使初始簇中心尽可能分散",具体步骤如下:
-
从样本集中随机选择1个样本作为第一个簇中心 μ 1 μ_1 μ1。
-
对每个样本 x i x_i xi,计算其到已选簇中心的最短距离 D ( x i ) D(x_i) D(xi)(即到最近簇中心的距离)。
-
根据 D ( x i ) D(x_i) D(xi)的平方值进行加权抽样,选择下一个簇中心 μ k ------ D ( x i ) μ_{k}------D(x_i) μk------D(xi)越大的样本,被选中的概率越高,确保新簇中心远离已选中心。
-
重复步骤2和3,直到选择出K个簇中心。
K-Means++通过优化初始簇中心,大幅提升了算法收敛到全局最优解的概率,同时减少了迭代次数,已成为主流的K-Means实现方式(如scikit-learn中的KMeans类默认采用K-Means++初始化)。
4.3 问题3:对异常值敏感如何解决?
K-Means的簇中心是样本均值,而均值对异常值极为敏感------一个极端异常值可能会将簇中心"拉偏",导致整个簇的划分结果失真。解决方案包括:
-
数据预处理剔除异常值:在聚类前,通过箱线图(IQR法则)、Z-score方法等识别并剔除异常值,从源头上减少异常值的影响。
-
使用中位数替代均值作为簇中心:中位数对异常值的抵抗力远强于均值,基于中位数的聚类算法称为K-Medoids(K-中心点算法),适用于异常值较多的场景,但计算成本高于K-Means。
-
引入加权K-Means:为每个样本分配权重,降低异常值的权重(如将异常值权重设为0.1,正常样本权重设为1),从而减少其对簇中心的影响。
4.4 问题4:不适用于非球形簇如何解决?
传统K-Means基于欧几里得距离,仅能有效聚类"球形分布"的簇(即簇内样本围绕中心呈圆形或椭圆形分布),对非球形簇(如环形、条形簇)的聚类效果极差。解决方案包括:
-
使用密度聚类算法辅助:如DBSCAN算法,基于样本的密度分布聚类,无需预设K值,能有效识别任意形状的簇,可先通过DBSCAN确定簇的大致形状和数量,再用K-Means细化聚类。
-
特征空间转换:通过核函数(如RBF核)将原始数据映射到高维特征空间,使非球形簇在高维空间中呈现球形分布,再使用K-Means聚类,即核K-Means(Kernel K-Means)。
5. K-Means聚类的特性与适用场景
明确K-Means的特性及适用场景,是合理选择聚类算法的关键,避免在不适用的场景中强行使用导致效果不佳。
5.1 核心特性
-
优点 :
简单直观,易于理解和实现,开发成本低。
-
计算效率高,时间复杂度为 O ( N ∗ K ∗ D ∗ T ) O(N*K*D*T) O(N∗K∗D∗T)(N为样本数,D为特征维度,T为迭代次数),适用于大规模数据。
-
可扩展性强,支持并行计算(如Spark MLlib中的K-Means实现),能处理百万级甚至亿级样本。
-
聚类结果易于解释,簇中心可直接对应业务含义(如用户簇中心的"消费金额"特征可代表该簇用户的平均消费能力)。
缺点:
-
需预设簇数K,难以准确确定最优K值。
-
对初始簇中心敏感,易收敛到局部最优解。
-
对异常值和噪声数据敏感,影响簇中心的准确性。
-
仅适用于球形分布的簇,对非球形、非凸形簇的聚类效果差。
-
对特征量纲敏感,需提前进行标准化处理。
5.2 适用场景
-
大规模数据的聚类任务:如电商平台的用户行为数据(百万级用户)、互联网日志数据(亿级访问记录),K-Means的高效性使其成为首选。
-
球形簇分布的数据场景:如客户价值细分(基于消费金额、购买频率等特征,客户自然形成高、中、低价值的球形簇)、图像像素聚类(同一物体的像素特征呈球形分布)。
-
业务中K值明确的场景:如根据业务需求将商品划分为固定类别的场景,无需通过算法确定K值,直接应用K-Means即可。
-
快速原型验证场景:在项目初期,需快速验证聚类思路的可行性时,K-Means的简单易用性使其能够快速输出聚类结果,为后续优化提供基准。
6. 总结
K-Means聚类是无监督学习的入门级算法,其"以簇中心为核心的迭代优化"逻辑简单高效,使其在大规模数据聚类任务中占据不可替代的地位。尽管存在需预设K值、对初始中心敏感等缺陷,但通过K-Means++、肘部法则、轮廓系数等优化方法,可有效提升其聚类效果。
二、scikit-learn中k-means聚类相关方法介绍
scikit-learn(sklearn)的sklearn.cluster.KMeans类是实现k-means聚类算法的核心工具,适用于无监督场景下的样本分组。
1. k-means聚类构造方法
k-means聚类的核心逻辑是通过迭代将样本划分为k个簇,使簇内样本相似度最大化、簇间相似度最小化。KMeans类通过参数配置聚类规则,初始化后得到聚类器对象。
1.1 方法签名及参数解释
基础签名:
python
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=8, init='k-means++', n_init='auto', max_iter=300,
tol=0.0001, random_state=None, algorithm='lloyd')核心参数解释:
| 参数名称 | 功能说明 |
|---|---|
n_clusters |
聚类的簇数量(k值),k-means算法的核心参数,决定最终分组数。 |
init |
初始聚类中心的初始化方法,影响算法收敛速度与最终结果。 |
n_init |
不同初始聚类中心的运行次数,取最优结果(最小惯性值)。 |
max_iter |
单次初始化下的最大迭代次数,迭代达到阈值则停止。 |
tol |
迭代收敛的容忍度,当簇中心变化量小于该值时停止迭代。 |
random_state |
随机种子,保证初始化和迭代过程的可复现性。 |
algorithm |
聚类算法的实现方式,影响计算效率和适用场景。 |
verbose |
日志输出级别,0为无输出,大于0时打印迭代过程。 |
copy_x |
是否复制原始数据,避免算法修改输入特征矩阵。 |
max_no_improvement |
连续无改进的迭代次数阈值,超过则提前停止(仅algorithm='elkan'生效)。 |
1.2 参数取值说明
| 参数名称 | 取值类型/范围 | 默认值 | 合法取值 | 取值说明与建议 |
|---|---|---|---|---|
n_clusters |
整数 | 8 | ≥1的整数 | 需结合业务场景或肘部法则确定,无固定最优值,常见范围2-10。 |
init |
字符串/数组 | 'k-means++' | 'k-means++'、'random'、形状为(k, n_features)的数组 | ① 'k-means++':智能初始化,避免初始中心过近,推荐使用;② 'random':随机选k个样本作为初始中心;③ 数组:自定义初始簇中心(需与特征维度匹配)。 |
n_init |
整数/'auto' | 'auto' | 正整数、'auto' | ① 'auto':init='k-means++'时取1,init='random'时取10;② 手动设为5-20,提升结果稳定性(但增加计算量)。 |
max_iter |
整数 | 300 | ≥1的整数 | 常见取值100-500,数据量大或特征多可适当增大,确保收敛。 |
tol |
浮点数 | 1e-4 | ≥0的浮点数 | 常用范围1e-4~1e-2,值越小收敛越严格,计算时间越长。 |
random_state |
整数/None/np.random.RandomState | None | 任意整数、None、RandomState对象 | 设为固定整数(如42)可复现结果,便于参数调优对比。 |
algorithm |
字符串 | 'lloyd' | 'lloyd'、'elkan'、'full' | ① 'lloyd':经典k-means算法,适用大数据,支持稀疏矩阵;② 'elkan':优化版,利用三角不等式减少距离计算,仅适用于稠密数据;③ 'full':等价于'lloyd'。 |
verbose |
整数 | 0 | ≥0的整数 | 0(无输出)、1(简要输出)、2(详细输出),调试时设为1即可。 |
copy_x |
布尔值 | True | True/False | ① True:复制数据,保护原始数据;② False:直接修改数据(节省内存),但原始数据会被覆盖。 |
max_no_improvement |
整数/None | None | ≥1的整数、None | None表示不限制,设为10-20可提前终止无改进的迭代,提升效率(仅elkan算法生效)。 |
2. k-means聚类构造方法返回对象的方法
KMeans初始化并通过fit()训练后,返回的聚类器对象提供一系列方法,覆盖聚类训练、预测、结果转换等核心功能,具体如下:
| 方法名称 | 语法格式 | 功能说明 |
|---|---|---|
fit(X) |
kmeans.fit(X) | 核心训练方法,输入特征矩阵X(形状[n_samples, n_features]),完成聚类迭代,更新簇中心等属性。 |
fit_predict(X) |
labels = kmeans.fit_predict(X) | 训练并直接返回样本的聚类标签(形状[n_samples,]),等价于先fit再predict。 |
predict(X) |
labels = kmeans.predict(X) | 对新样本X预测所属簇标签,需先调用fit()训练模型。 |
transform(X) |
dist = kmeans.transform(X) | 计算每个样本到各簇中心的欧氏距离,返回形状[n_samples, n_clusters]的矩阵。 |
fit_transform(X) |
dist = kmeans.fit_transform(X) | 训练并直接返回样本到簇中心的距离矩阵,等价于先fit再transform。 |
score(X) |
score = kmeans.score(X) | 计算聚类的负惯性值(-inertia_),值越大表示聚类效果越好(簇内越紧凑)。 |
inertia_(属性) |
注:是属性而非方法,此处补充 | 计算簇内平方和(惯性值),即每个样本到其簇中心的欧氏距离平方和,是评估聚类紧凑性的核心指标。 |
get_params() |
params = kmeans.get_params() | 返回模型的参数配置字典,便于查看当前参数或后续调参。 |
set_params(**params) |
kmeans.set_params(n_clusters=5) | 修改模型参数,无需重新初始化对象,支持动态调整(如n_clusters、max_iter)。 |
3. k-means聚类构造方法返回对象的属性
KMeans对象经fit()训练后,生成一系列只读属性,存储聚类核心结果,所有属性需在训练后获取有效值,具体如下:
| 属性名称 | 数据类型 | 功能说明 |
|---|---|---|
cluster_centers_ |
数组(形状[n_clusters, n_features]) | 存储各簇的中心坐标,每个行向量对应一个簇的中心,是聚类的核心结果。 |
labels_ |
数组(形状[n_samples,]) | 存储训练集样本的聚类标签,标签为0~n_clusters-1的整数,对应样本所属簇。 |
inertia_ |
浮点数 | 簇内平方和(惯性值),即所有样本到其簇中心的欧氏距离平方和,值越小簇内越紧凑。 |
n_iter_ |
整数 | 实际迭代次数,若小于max_iter,说明算法提前收敛(簇中心变化≤tol)。 |
n_features_in_ |
整数 | 训练模型时使用的特征数量,与输入X的特征维度一致。 |
feature_names_in_ |
数组(可选) | 训练数据为DataFrame时,存储特征名称;数组形状[n_features_in_]。 |
tol_ |
浮点数 | 实际使用的收敛容忍度(与构造参数tol一致)。 |
核心属性使用说明:
cluster_centers_:可用于解释各簇的特征特征(如簇1的"平均消费金额"为500元),是聚类结果业务解读的核心依据;labels_:可与原始数据合并,分析不同簇的样本分布规律;inertia_:是"肘部法则"确定最优k值的核心指标,需结合不同k值的inertia_曲线判断。
4. k-means聚类模型评估指标
k-means聚类属于无监督学习,无"真实标签"参考,评估核心围绕"簇内紧凑性""簇间分离度"展开,常用指标如下:
| 指标名称 | 计算逻辑 | 取值范围 | 评估标准 | sklearn实现函数 |
|---|---|---|---|---|
| 惯性值(Inertia) | 所有样本到其簇中心的欧氏距离平方和 | [0, +∞) | 值越小,簇内越紧凑;但随k值增大单调递减,需结合肘部法则判断最优k。 | 直接调用kmeans.inertia_,无单独函数 |
| 轮廓系数(Silhouette Score) | 综合簇内紧凑性(a)和簇间分离度(b),计算每个样本的轮廓系数:(b-a)/max(a,b),再取平均值。 | [-1, 1] | 越接近1,聚类效果越好(样本与自身簇紧凑,与其他簇分离);≤0说明聚类重叠严重。 | sklearn.metrics.silhouette_score(X, labels) |
| 戴维斯-布尔丁指数(DBI) | 计算各簇的"簇内散度/簇间距离"的平均值,衡量簇的紧凑性与分离度。 | [0, +∞) | 值越小,聚类效果越好;通常<1为优秀,1~2为良好,>3为较差。 | sklearn.metrics.davies_bouldin_score(X, labels) |
| 卡尔斯基-哈拉巴斯指数(CHI) | 计算"簇间方差和/簇内方差和"×(样本数-簇数)/(簇数-1),反映簇间分离度。 | [0, +∞) | 值越大,聚类效果越好;对噪声和异常值较敏感。 | sklearn.metrics.calinski_harabasz_score(X, labels) |
三、pandas.DataFrame中的绘图方法
1. 绘图方法介绍
pandas.DataFrame 内置了 plot() 方法(基于 matplotlib 封装),无需额外导入绘图库即可快速实现数据可视化,支持多种常见图表类型,满足数据分析中的快速探索需求。其核心优势是与 DataFrame 数据结构深度兼容,能直接读取列/行数据作为绘图数据源,无需手动处理数据格式转换。
常用的图表类型通过 kind 参数指定,核心支持以下几种:
- 折线图(line):默认类型,适合展示数据随时间或有序维度的变化趋势,例如时序数据的波动情况。
- 柱状图(bar/barh) :
bar为垂直柱状图,barh为水平柱状图,适合对比不同类别数据的数值大小,支持分组对比。 - 直方图(hist):用于展示数据的分布特征,自动对数据进行分箱统计,直观呈现数据集中趋势和离散程度。
- 散点图(scatter) :需指定
x和y列,用于分析两个变量之间的相关性,例如身高与体重的关联关系。 - 箱线图(box):展示数据的四分位数、中位数和异常值,快速识别数据中的离群点和分布离散度。
- 饼图(pie) :需配合
y参数指定数值列,展示各类别数据占总体的比例,要求数据非负且总和有实际意义。
2. 参数介绍
DataFrame.plot() 方法的参数丰富,可灵活控制图表样式、布局和数据映射,核心常用参数如下(按功能分类)。
2.1 图表类型与数据映射参数
| 参数名 | 作用 | 可选值/说明 |
|---|---|---|
kind |
指定图表类型 | 默认为 'line',可选 'bar'/'barh'/'hist'/'scatter'/'box'/'pie'/'kde' 等 |
x |
指定x轴数据源(仅散点图、柱状图等需显式指定) | DataFrame 列名或数组 |
y |
指定y轴数据源 | DataFrame 列名(单个或列表)、数组,饼图需指定单个数值列 |
data |
可选,指定绘图数据源 | 若未指定,默认使用调用 plot() 的 DataFrame |
2.2 图表样式与标签参数
| 参数名 | 作用 | 可选值/说明 |
|---|---|---|
title |
设置图表标题 | 字符串,支持换行(\n) |
xlabel/ylabel |
设置x轴/y轴标签 | 字符串 |
color |
设置线条/填充颜色 | 单个颜色值(如 'red'、'#FF0000')或颜色列表(对应多列数据) |
alpha |
设置颜色透明度 | 浮点数(0~1),0为完全透明,1为不透明 |
linestyle |
设置线条样式(仅折线图) | 默认为 '-'(实线),可选 '--'(虚线)、':'(点线)、'-.'(点划线) |
linewidth |
设置线条宽度(仅折线图) | 正整数 |
marker |
设置数据点标记(仅折线图、散点图) | 如 'o'(圆点)、's'(正方形)、'^'(三角形) |
2.3 布局与显示参数
| 参数名 | 作用 | 可选值/说明 |
|---|---|---|
figsize |
设置图表尺寸 | 元组 (宽度, 高度),单位为英寸(如 (10, 6)) |
grid |
是否显示网格线 | 布尔值(默认 False),可指定 grid=True 显示 |
legend |
是否显示图例 | 布尔值(默认 True,多列数据时自动生成),False 隐藏图例 |
subplots |
是否将多列数据拆分为子图 | 布尔值(默认 False),True 时每列数据对应一个子图 |
layout |
子图布局(仅 subplots=True 时生效) |
元组 (行数, 列数),如 (2, 2) 表示2行2列子图 |
2.4 特定图表专属参数
| 参数名 | 适用图表 | 作用 | 可选值/说明 |
|---|---|---|---|
bins |
直方图 | 指定分箱数量 | 正整数(默认自动分箱) |
autopct |
饼图 | 显示百分比标签 | 格式化字符串(如 '%1.1f%%' 表示保留1位小数) |
startangle |
饼图 | 设置起始角度 | 整数(默认0°,顺时针旋转) |
bins |
直方图 | 数据分箱数 | 整数或数组(指定分箱边界) |
vert |
直方图/柱状图 | 是否垂直显示 | 布尔值(默认 True,直方图设为 False 则水平显示) |
3. 使用示例
示例代码(以常见图表为例):
python
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 构造示例数据
data = pd.DataFrame({
'A': np.random.randn(100).cumsum(), # 累积和模拟时序数据
'B': np.random.randint(10, 50, 100), # 随机整数数据
'C': np.random.choice(['X', 'Y', 'Z'], 100), # 分类数据
'D': np.random.normal(50, 10, 100) # 正态分布数据
})
# 1. 折线图(默认):展示A列时序趋势
# data['A'].plot(title='A列时序变化趋势')
# 综合参数示例:定制化折线图
data['A'].plot(
kind='line', # 图表类型
title='A列时序趋势(定制样式)', # 标题
xlabel='索引', ylabel='数值', # 轴标签
color='#2E86AB', linewidth=2, linestyle='--', # 线条样式
marker='o', markersize=4, # 数据点标记
figsize=(10, 4), grid=True, alpha=0.8 # 布局与透明度
)
# 2. 垂直柱状图:对比前10行A、B列数据
data[['A', 'B']].head(10).plot(kind='bar', title='A、B列前10行数据对比')
# 3. 直方图:展示D列数据分布
data['D'].plot(kind='hist', bins=15, title='D列数据分布')
# 4. 散点图:分析A与B的相关性
data.plot(kind='scatter', x='A', y='B', title='A与B的散点图')
# 5. 箱线图:展示A、B列数据分布特征
data[['A', 'B']].plot(kind='box', title='A、B列箱线图')
# 6. 饼图:展示C列各类别占比
data['C'].value_counts().plot(kind='pie', autopct='%1.1f%%', title='C列类别占比')
plt.show()四、基于K-Means的鸢尾花数据聚类分析
K-Means是无监督学习中最经典的聚类算法之一,核心思想是通过迭代将样本划分为指定数量的簇,使簇内样本相似度最大化、簇间相似度最小化。鸢尾花数据集作为机器学习经典数据集,特征维度低、数据分布规律,非常适合用于K-Means聚类的实战分析。本文将从数据挖掘目标出发,完成数据收集加载、预处理、聚类建模、结果评估全流程,清晰展示K-Means在鸢尾花数据上的应用效果。
1. 数据挖掘目标
本次基于K-Means的鸢尾花数据聚类分析,核心目标分为以下3点:
- 验证聚类有效性:鸢尾花数据集包含3类已知品种的样本(山鸢尾、变色鸢尾、维吉尼亚鸢尾),通过K-Means聚类将样本划分为3个簇,验证无监督聚类结果与真实品种标签的匹配度,评估K-Means算法的聚类效果;
- 挖掘特征规律:分析聚类后各簇的特征分布(如花瓣长度、萼片宽度等),总结不同簇的核心特征差异,解读聚类结果的业务意义;
- 掌握K-Means实战流程:完整落地"数据加载→预处理→模型构建→参数调优→结果评估→可视化"的K-Means聚类流程,形成可复用的无监督分析模板。
2. 数据收集与加载
2.1 数据集介绍
本示例使用的鸢尾花数据集(Iris Dataset) 是机器学习领域最经典的数据集之一,由英国统计学家和生物学家罗纳德·费希尔(Ronald Fisher)于1936年提出,常被用于分类、聚类算法的验证与演示。
| 字段名称(英文) | 中文含义 | 数据类型 | 单位 | 说明 |
|---|---|---|---|---|
sepal length (cm) |
花萼长度 | 浮点数 | 厘米 | 花朵最外层保护结构的长度 |
sepal width (cm) |
花萼宽度 | 浮点数 | 厘米 | 花萼的横向宽度 |
petal length (cm) |
花瓣长度 | 浮点数 | 厘米 | 花朵内层显眼部分的长度 |
petal width (cm) |
花瓣宽度 | 浮点数 | 厘米 | 花瓣的横向宽度 |
species |
类别标签 | 对象 | --- | 3个类别标签:setosa(山鸢尾,标签0)、versicolor(变色鸢尾,标签1)、virginica(维吉尼亚鸢尾,标签2) |
所有特征均为形态学测量值,具有明确的生物学意义,且数值范围相近,适合直接用于建模(必要时可标准化)。
2.2 数据加载
鸢尾花数据集已内置在scikit-learn的datasets模块中,可直接调用加载,无需手动下载。
python
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.datasets import load_breast_cancer, load_iris
from sklearn.tree import DecisionTreeClassifier
# 设置中文字体正常显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置Pandas全局选项
pd.set_option('display.max_columns', None)
pd.set_option('display.width', None)
pd.set_option('display.max_colwidth', 50)
pd.set_option('display.expand_frame_repr', False)
# ====================加载数据====================
# 加载鸢尾花数据集
iris = load_iris()
# 转换为DataFrame
df_iris = pd.DataFrame(
data=iris.data, # 特征矩阵
columns=iris.feature_names # 特征名称
)
# 添加真实品种标签列(用于后续对比聚类结果)
df_iris['species'] = iris.target
# 将数字标签映射为品种名称(提升可读性)
df_iris['species_name'] = (df_iris['species'].map({
0: '山鸢尾',
1: '变色鸢尾',
2: '维吉尼亚鸢尾'
}))3. 探索性数据分析
探索性数据分析(EDA)是聚类建模前的核心环节,旨在通过统计分析和可视化手段挖掘数据内在规律------包括特征分布特征、特征间关联关系及不同品种的特征差异,为后续K-Means聚类的参数设置、结果解读提供依据。
3.1 数据基本信息
在聚类建模前,首先对鸢尾花数据集的基础信息进行梳理,明确数据规模、结构、完整性与统计特征,为后续分析奠定基础。
python
# ====================数据基本信息====================
# 基础信息探索
print("=== 鸢尾花数据集基础信息 ===")
print(f"数据集形状:{df_iris.shape}(样本数×特征数)")
print("\n=== 数据前5行预览 ===")
print(df_iris.head())
print("\n=== 数据类型与缺失值检查 ===")
print(df_iris.info()) # 无缺失值,特征均为浮点型
print("\n=== 特征统计描述 ===")
print(df_iris.describe().round(2)) # 查看特征的均值、标准差等鸢尾花数据集共包含150个样本,每个样本对应4个数值型特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度),以及2个标签列(species为数值型品种标签、species_name为文字型品种名称),整体结构清晰规范。
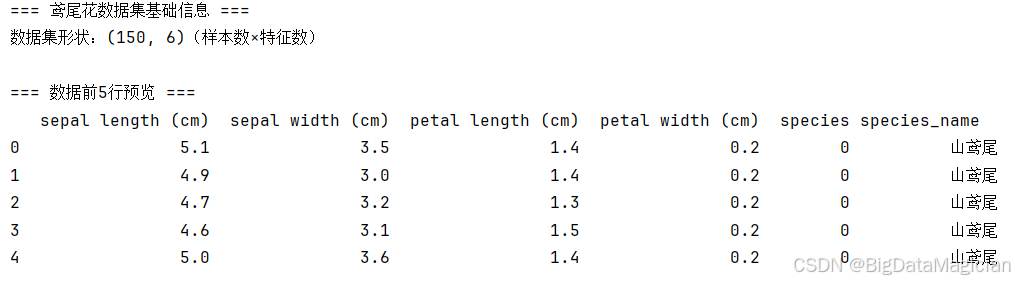
通过数据类型与缺失值检查可知,所有特征列均无缺失值,4个形态特征为浮点型,标签列分别为整数型与字符型,数据质量较高,无需进行缺失值填充等预处理操作。

从统计描述结果可见,不同特征的数值范围差异较大(如花瓣长度最小值1.0cm、最大值6.9cm,标准差达1.77),花萼宽度的波动相对较小(标准差0.44);各特征的均值与中位数(50%分位数)接近,说明多数特征的分布相对对称,无极端偏离的异常值。
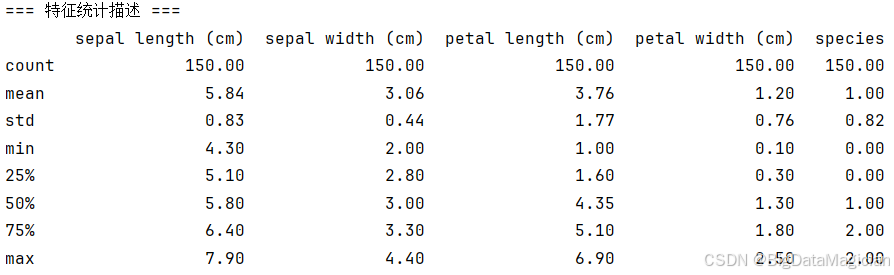
3.2 单特征分布分析
单特征分布是挖掘数据内在规律的基础环节,通过核密度估计图(KDE)可直观呈现鸢尾花4个形态特征的整体分布形态,为后续聚类的"簇划分依据"提供参考。本次分析针对花萼长度、花萼宽度、花瓣长度、花瓣宽度4个特征,分别绘制核密度曲线,以观察各特征的集中趋势与离散特性。可视化中对每个特征单独生成核密度图(填充式曲线更清晰展示分布区间),并开启单独归一化避免样本量干扰。
python
# ====================单特征分布分析====================
import matplotlib.pyplot as plt
import seaborn as sns
# 绘制核密度图,KDE:核密度估计
plt.figure(figsize=(15, 10))
feature = df_iris.columns[:-2]
for i in range(len(feature)):
plt.subplot(2, 2, i + 1)
sns.kdeplot(
data=df_iris,
x=feature[i],
fill=True,
common_norm=False, # 每个类别单独归一化
alpha=0.5
)
plt.title(f'按类别的 {feature[i]} 核密度估计图')
plt.xlabel(feature[i])
plt.tight_layout()
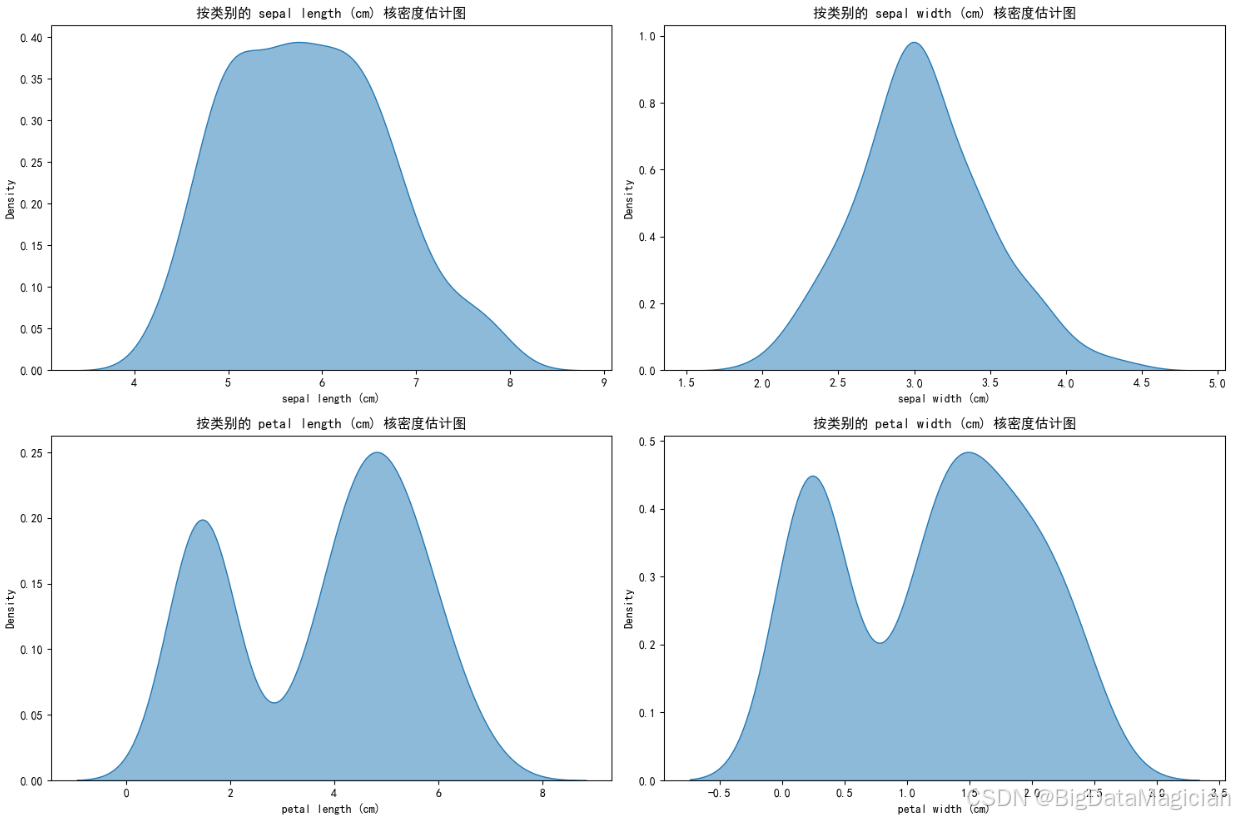
plt.savefig('单特征分布核密度估计图.png')从结果可总结出两个核心特征:
(1)分布形态差异
4个形态特征的分布形态呈现明显分化:
- 花萼长度、花萼宽度的核密度曲线呈单峰对称形态,符合近似正态分布的特征,说明这两个特征的数值集中在均值附近,离散程度相对温和;
- 花瓣长度、花瓣宽度的核密度曲线呈现双峰形态,曲线中间存在明显的"低谷"区域------这是鸢尾花不同品种在花瓣形态上差异显著的直接体现,两类峰值分别对应不同品种的特征集中区间。
(2)特征离散特性
不同特征的离散程度差异较大:
- 花萼相关特征(长度、宽度)的分布区间相对紧凑,曲线峰值较高,说明多数样本的花萼尺寸集中在较小范围内;
- 花瓣相关特征(长度、宽度)的分布区间更宽,且因"双峰"结构呈现明显的"两极分化",这也暗示花瓣特征更可能成为区分不同样本群体的核心依据。
这一结果为后续K-Means聚类提供了重要线索:花瓣特征的"双峰分布"意味着数据天然存在群体划分的基础,聚类过程中这些特征将成为区分不同簇的关键驱动因素。
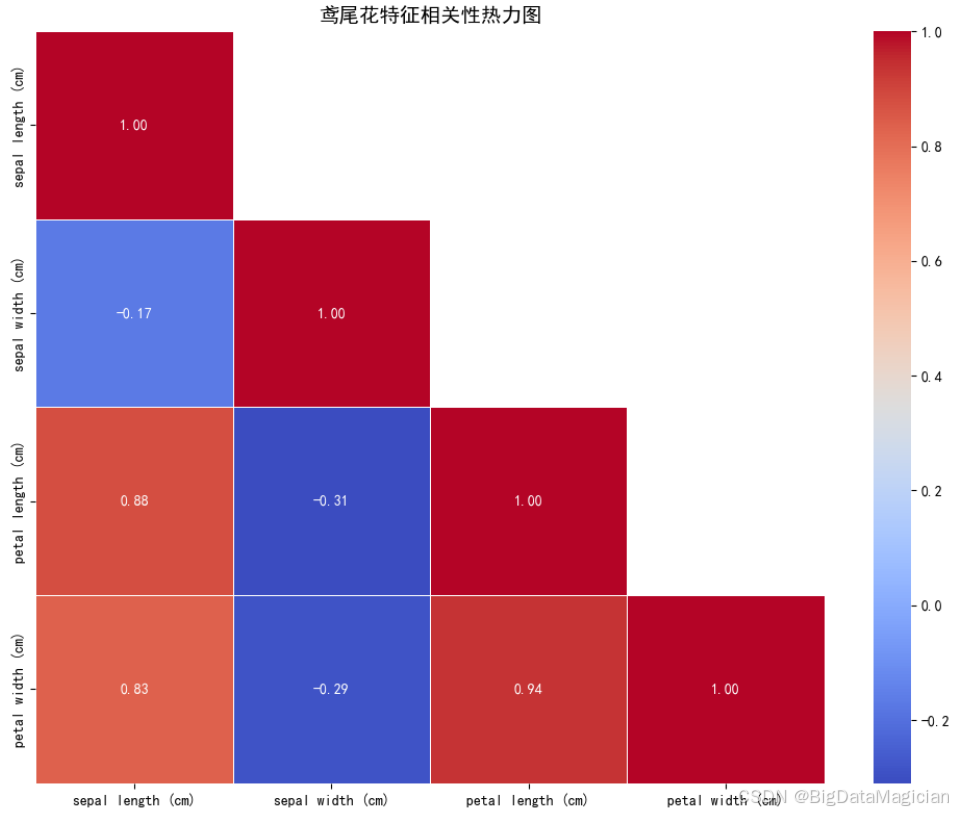
3.2 特征间相关性分析
特征间的相关性是聚类分析的关键参考------高相关特征会强化该维度对聚类结果的影响,而低相关特征则体现了数据的多维度差异。本次通过斯皮尔曼相关系数结合热力图,分析鸢尾花4个形态特征的线性关联程度。可视化中隐藏了热力图的上三角区域(避免信息重复),以颜色深浅+数值标注的方式呈现相关系数(红色代表正相关、蓝色代表负相关,数值越接近±1关联越强)。
python
# ===================特征间相关性分析====================
import matplotlib.pyplot as plt
import seaborn as sns
features = df_iris.columns[:-2]
# 全局特征相关性热力图(不区分品种)
plt.figure(figsize=(10, 8))
# 计算特征间的皮尔逊相关系数
corr_matrix = df_iris[features].corr(method='spearman')
# 绘制热力图
mask = np.triu(m=np.ones_like(corr_matrix, dtype=bool), k=1) # 隐藏上三角(避免重复)
sns.heatmap(data=corr_matrix, mask=mask, annot=True, fmt='.2f', cmap='coolwarm', linewidths=0.5)
plt.title('鸢尾花特征相关性热力图', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.savefig('特征间全局相关性.png')从相关性分析热力图可以看出,花瓣相关特征之间及其与花萼长度呈现出显著的正相关关系------花瓣长度与花瓣宽度的相关系数高达0.94,几乎呈线性关联;同时,二者与花萼长度的相关系数也分别达到0.88和0.83。这表明鸢尾花的花瓣尺寸与花萼长度存在明显的协同变化趋势,花瓣越长或越宽,花萼通常也越长。花萼宽度与其他特征的关联较弱,表现为弱负相关(与花萼长度、花瓣长度、花瓣宽度的相关系数分别为-0.17、-0.31和-0.29),说明其变化相对独立。这一特性在K-Means聚类中具有重要意义,强相关的花瓣特征与花萼长度共同强化了"花部整体尺寸"这一聚类主维度,而花萼宽度的独立性则可能为簇的细分提供额外的判别信息。
3.3 变异系数分析
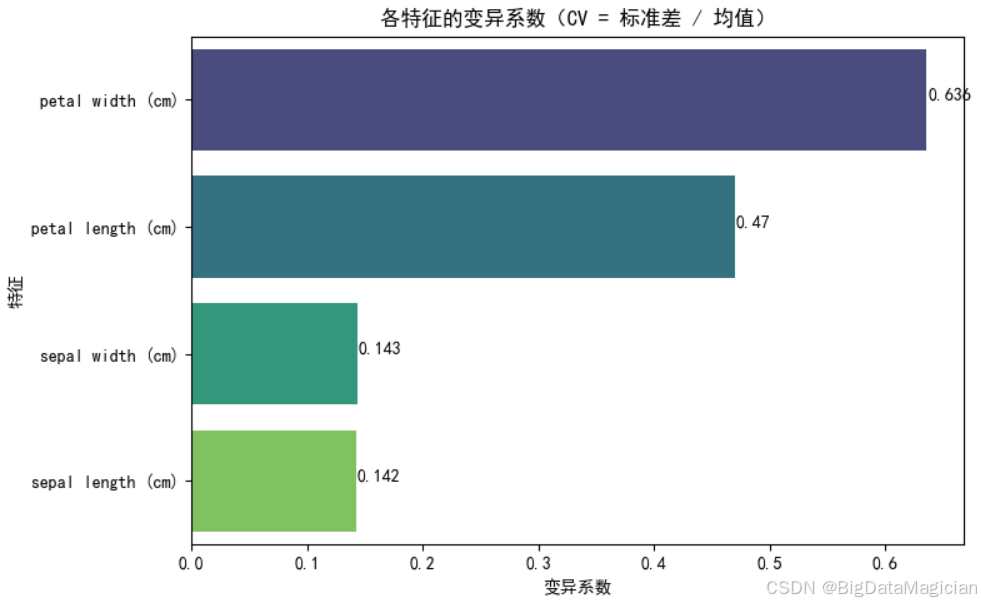
变异系数(CV)是衡量特征离散程度的标准化指标,可消除特征尺度差异的影响,更客观地对比不同特征的波动程度------变异系数越大,说明该特征在样本间的差异越显著,越可能成为聚类的区分依据。本次分析计算了鸢尾花4个形态特征的变异系数,并以条形图可视化排序结果。
python
# ===================特征变异系数分析====================
# 计算各特征的变异系数(反映离散程度,变异系数=标准差/均值)
cv_data = []
for feat in df_iris.columns[:-2]:
cv = df_iris[feat].std() / df_iris[feat].mean()
cv_data.append({'特征': feat, '变异系数': round(cv, 3)})
cv_df = pd.DataFrame(cv_data).sort_values('变异系数', ascending=False)
print("各特征变异系数(离散程度):")
print(cv_df)
plt.figure(figsize=(8, 5))
sns.barplot(data=cv_df, x='变异系数', y='特征', hue='特征', palette='viridis')
# 添加数值标签
for index, value in enumerate(cv_df['变异系数']):
plt.text(x=value + 0.001, y=index, s=value)
plt.title('各特征的变异系数(CV = 标准差 / 均值)')
plt.xlabel('变异系数')
plt.ylabel('特征')
plt.tight_layout()
plt.savefig('变异系数条形图.png')从图中可明确特征的离散程度差异,花瓣宽度的变异系数达0.636,花瓣长度的变异系数为0.47,二者是所有特征中离散程度最高的------这意味着不同样本的花瓣尺寸差异显著,与之前单特征分布的"双峰"规律一致;花萼宽度(0.143)与花萼长度(0.142)的变异系数接近且数值较小,说明这两个特征在样本间的波动相对温和,个体差异不明显。
这一结果进一步强化了"花瓣特征是区分鸢尾花群体核心依据"的结论,高变异系数的特征包含更丰富的群体差异信息,将成为K-Means聚类中"簇划分"的主要驱动维度;而低变异系数的萼片特征则更多体现样本的共性,对聚类结果的影响相对有限。
4. 数据预处理
K-Means聚类算法基于欧氏距离计算样本相似度,对特征的尺度和分布敏感------若不同特征的数值范围差异较大(如"花瓣长度"以厘米为单位,"花瓣宽度"以毫米为单位),会导致距离计算偏向数值范围大的特征,影响聚类结果的公平性。因此,在建模前需对数据进行标准化预处理,消除特征尺度差异,同时验证数据无异常值干扰,确保聚类结果的可靠性。
4.1 异常值检测与处理
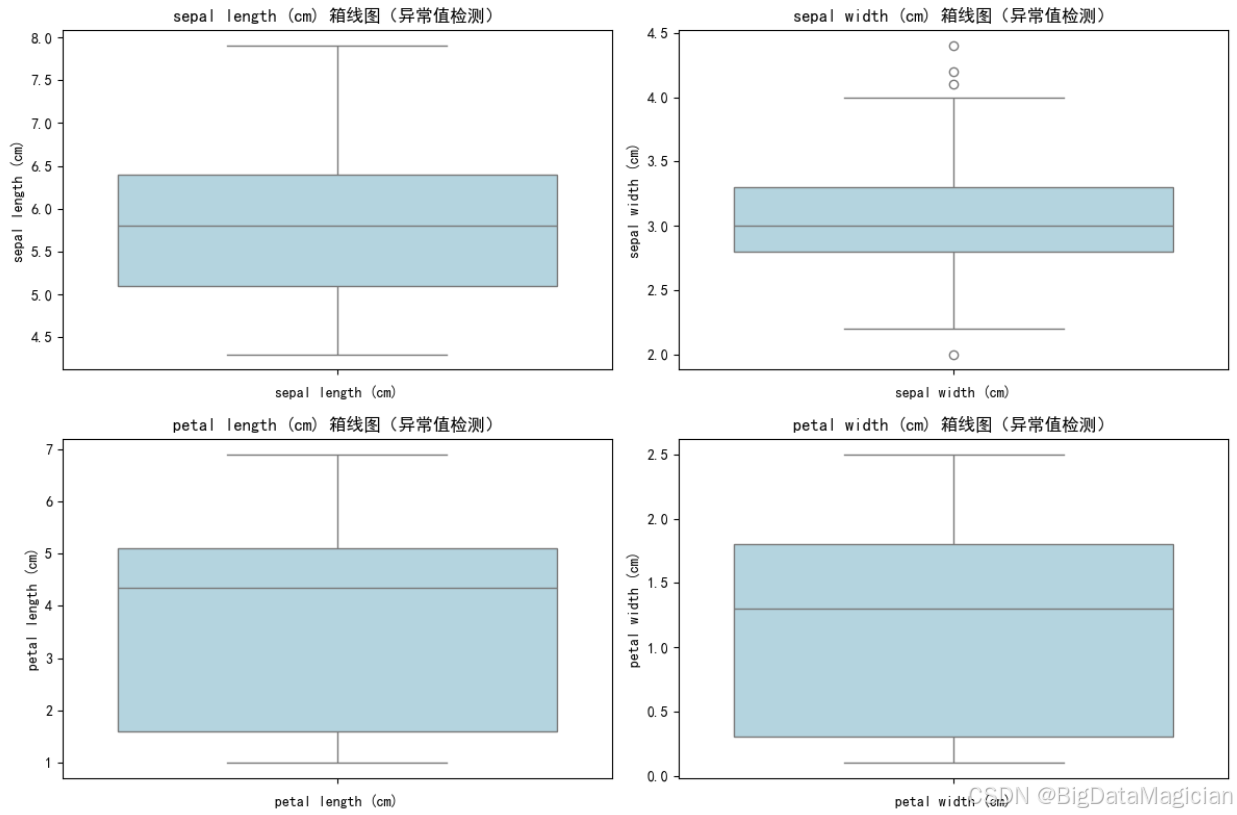
异常值会干扰K-Means聚类中心的计算(聚类对极值敏感),因此需在建模前通过箱线图法识别并评估异常值的影响。箱线图基于四分位距(IQR)判定异常值,当样本值超出"Q1-1.5×IQR"(下界)或"Q3+1.5×IQR"(上界)时,判定为异常值。本次分析对4个形态特征分别绘制箱线图,并定量统计异常值数量与占比。
python
# ====================异常值检测与处理====================
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# 提取4个形态特征
features = df_iris.columns[:-2]
# 绘制箱线图检测异常值
plt.figure(figsize=(12, 8))
for i, feat in enumerate(features):
plt.subplot(2, 2, i + 1)
sns.boxplot(data=df_iris, y=feat, color='lightblue')
plt.title(f'{feat} 箱线图(异常值检测)')
plt.xlabel(feat)
plt.tight_layout()
plt.savefig('特征箱线图_异常值检测.png')
# 定量计算异常值数量
outlier_info = {}
for feat in features:
# 计算四分位数和IQR
Q1 = df_iris[feat].quantile(0.25)
Q3 = df_iris[feat].quantile(0.75)
IQR = Q3 - Q1
# 异常值判定条件
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
# 统计异常值数量
outliers = df_iris[(df_iris[feat] < lower_bound) | (df_iris[feat] > upper_bound)]
outlier_info[feat] = {
'下界': round(lower_bound, 2),
'上界': round(upper_bound, 2),
'异常值数量': len(outliers),
'异常值占比': f'{round(len(outliers) / len(df_iris) * 100, 2)}%'
}
# 输出异常值统计结果
outlier_df = pd.DataFrame(outlier_info).T
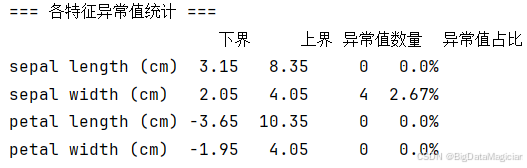
print("=== 各特征异常值统计 ===")
print(outlier_df)从图中可以看到,箱线图中仅"花萼宽度"出现少量离散的异常值点,花萼长度、花瓣长度、花瓣宽度的箱线图无明显超出上下界的点;
从图中可以看到,花萼宽度的异常值数量为4个,占比不足3%,其余特征无异常值。结合鸢尾花的生物学特性,花萼宽度的异常值属于"合理的个体形态差异"(数值仅略偏离正常区间),并非数据错误。考虑到异常值占比极低且不影响整体数据分布,本次选择保留异常值,避免因删除样本破坏数据集的完整性,同时保证后续聚类结果更贴合实际样本的形态差异。
4.2 特征标准化
K-Means聚类的核心是基于样本间的距离(如欧氏距离)划分簇,而特征尺度差异会导致距离计算偏向数值范围大的特征(如鸢尾花的花瓣长度数值波动大于花萼宽度,未标准化时会主导距离计算)。因此,需通过标准化消除特征尺度的影响,保证各特征在聚类中权重均衡。本次采用Z-Score标准化,将4个形态特征转换为"均值为0、标准差为1"的标准正态分布。
python
# ====================特征标准化====================
from sklearn.preprocessing import StandardScaler
# 提取特征矩阵(仅保留4个形态特征)
X = df_iris[features].values
# 初始化标准化器
scaler = StandardScaler()
# 拟合并转换数据
X_scaled = scaler.fit_transform(X)
# 将标准化后的数据转换为DataFrame,便于后续分析
df_iris_scaled = pd.DataFrame(
X_scaled,
columns=features
)
# 保留标签列(用于后续对比聚类结果)
df_iris_scaled['species'] = df_iris['species']
df_iris_scaled['species_name'] = df_iris['species_name']
# 验证标准化效果
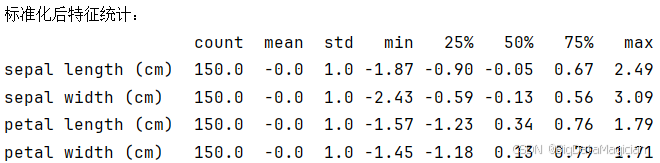
print("标准化后特征统计:")
print(df_iris_scaled[features].describe().T.round(2))从标准化后的特征统计结果可见,所有特征的均值均接近0,标准差统一为1,成功消除了原特征间的尺度差异;各特征的极值(min/max)分布在-2.5~3.5区间内,数值范围一致,确保后续距离计算中各特征的贡献度对等。标准化后的特征矩阵既保留了原特征的分布形态与相对差异,又避免了尺度偏差对聚类结果的干扰,为K-Means聚类提供了公平的特征输入。
5. 模型构建(模型选择、训练)
5.1 确定最优聚类数k
聚类数k是K-Means的核心参数,直接决定簇的划分结果。本次通过肘部法则 (基于惯性值)和轮廓系数(基于簇内紧凑度与簇间分离度)结合的方式,从"簇内相似度"和"簇间区分度"两个维度筛选最优k值,测试范围为2~10。
python
# ====================肘部法和轮廓系数法则确定最优k值====================
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score
# 测试k值范围:2~10
k_range = range(2, 11)
# 存储不同k值的惯性值
inertias = []
# 存储不同k值的轮廓系数
sil_scores = []
for k in k_range:
kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
kmeans.fit(X_scaled)
inertias.append(kmeans.inertia_)
labels = kmeans.predict(X_scaled)
sil_score = silhouette_score(X_scaled, labels)
sil_scores.append(sil_score)
df_k = pd.DataFrame({
'k': k_range,
'惯性值': inertias,
'轮廓系数': sil_scores
})
print(f"各k值对应的惯性值和轮廓系数:\n{df_k}")
# 绘制肘部法则图
plt.figure(figsize=(14, 5))
plt.subplot(1, 2, 1)
plt.plot(k_range, inertias, 'o-', color='#2E86AB', linewidth=2, markersize=8)
for x, y in zip(k_range, inertias):
plt.text(x=x, y=y + 3, s=f'{y:.2f}')
plt.title('K-Means肘部法则图(惯性值 vs k值)')
plt.xlabel('聚类数k', fontsize=12)
plt.ylabel('惯性值(Inertia)', fontsize=12)
plt.xticks(k_range)
plt.grid(alpha=0.3)
# 绘制轮廓系数曲线
plt.subplot(1, 2, 2)
plt.plot(k_range, sil_scores, 'o-', color='#F18F01', linewidth=2, markersize=8)
for x, y in zip(k_range, sil_scores):
plt.text(x=x, y=y + 0.01, s=f'{y:.3f}', ha='center')
plt.title('K-Means轮廓系数图(轮廓系数 vs k值)', fontsize=14, fontweight='bold')
plt.xlabel('聚类数k', fontsize=12)
plt.ylabel('轮廓系数(Silhouette Score)', fontsize=12)
plt.xticks(k_range)
plt.grid(alpha=0.3)
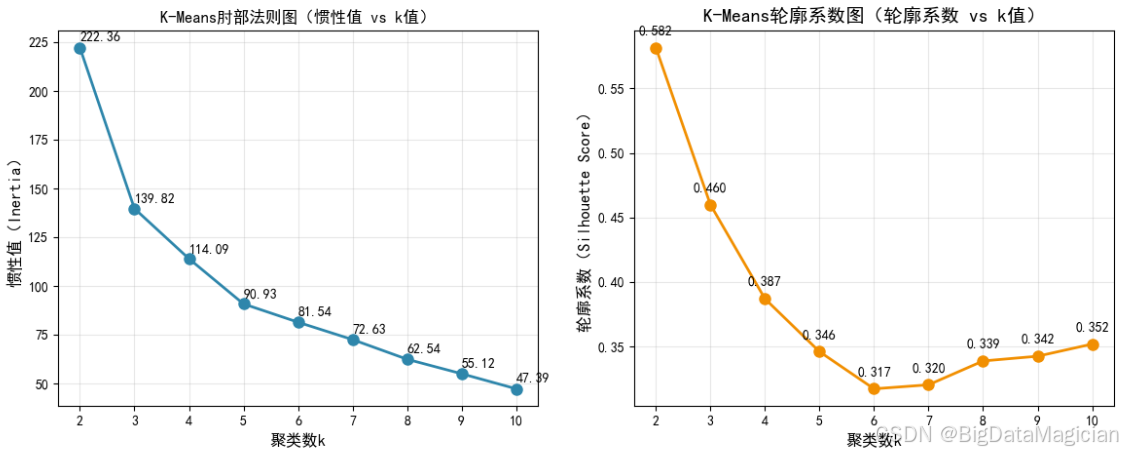
plt.savefig('KMeans肘部法则图和轮廓系数图.png')肘部法则(惯性值分析) :惯性值代表簇内所有样本到其簇中心的欧氏距离平方和,值越小说明簇内样本越紧凑;当k从2增加到4时,惯性值从222.36快速下降(k=2→3:下降83.08;k=3→4:下降25.73),说明簇内紧凑度提升明显;当k≥4后,惯性值的下降幅度逐渐放缓(如k=4→5仅下降19.16),曲线出现"肘部拐点",提示k=3~4是簇内紧凑度的合理临界点。
轮廓系数分析:轮廓系数的取值范围为[-1,1],值越接近1说明簇内样本越紧凑、簇间区分度越高;当k=2时,轮廓系数达0.682(最高值),但对应簇数与鸢尾花实际3个品种不符;当k=3时,轮廓系数为0.460(处于较高水平),既保证了簇的区分度,又与数据的实际类别数量一致;当k>3后,轮廓系数持续下降(k=6时降至0.317),说明簇划分过细导致簇间差异模糊。
结合鸢尾花数据集的实际品种数(3类),最终确定最优聚类数k=3------该k值既满足肘部法则的紧凑度要求,又具备较高的轮廓系数,同时契合数据的真实类别分布。
5.2 K-Means聚类模型构建
基于最优聚类数( k=3 ),初始化K-Means模型并在标准化后的特征矩阵上完成训练,输出聚类标签、簇中心(含标准化与原始尺度)等核心结果,为后续分析提供依据。
python
# ====================K-Means模型训练====================
from sklearn.cluster import KMeans
# 初始化K-Means模型(最优k=3)
kmeans = KMeans(n_clusters=3, random_state=42, n_init=10)
# 训练模型(输入标准化后的特征矩阵)
kmeans.fit(X_scaled)
# 获取聚类核心结果
cluster_labels = kmeans.labels_ # 所有样本的聚类标签(0/1/2)
cluster_centers = kmeans.cluster_centers_ # 3个簇的中心(标准化后,维度:3×4)
inertia = kmeans.inertia_ # 最终惯性值(簇内紧凑度指标)
# 将聚类标签合并到预处理后的DataFrame,便于后续分析
df_iris_scaled['cluster_label'] = cluster_labels
df_iris_scaled.to_csv('标准化后的聚类结果.csv', index=False)
df_iris_new = df_iris.copy()
df_iris_new['cluster_label'] = cluster_labels
df_iris_new.to_csv('原始数据的聚类结果.csv', index=False)
# 输出训练结果摘要
print("=== K-Means模型训练结果 ===")
print(f"最终聚类标签分布:\n{pd.Series(cluster_labels).value_counts().sort_index()}")
print(f"\n模型最终惯性值:{inertia:.2f}")
print(f"\n标准化后的簇中心:")
cluster_centers_scaled = pd.DataFrame(
cluster_centers,
columns=df_iris.columns[:-2], # 特征名称
index=[f'簇{i + 1}' for i in range(3)] # 簇名称
)
print(cluster_centers_scaled.round(3))
# 簇中心逆标准化(还原为原始尺度cm,便于业务解读)
cluster_centers_original = scaler.inverse_transform(cluster_centers)
cluster_centers_original = pd.DataFrame(
cluster_centers_original,
columns=df_iris.columns[:-2],
index=[f'簇{i + 1}' for i in range(3)]
)
print(f"\n原始尺度的簇中心(单位:cm):")
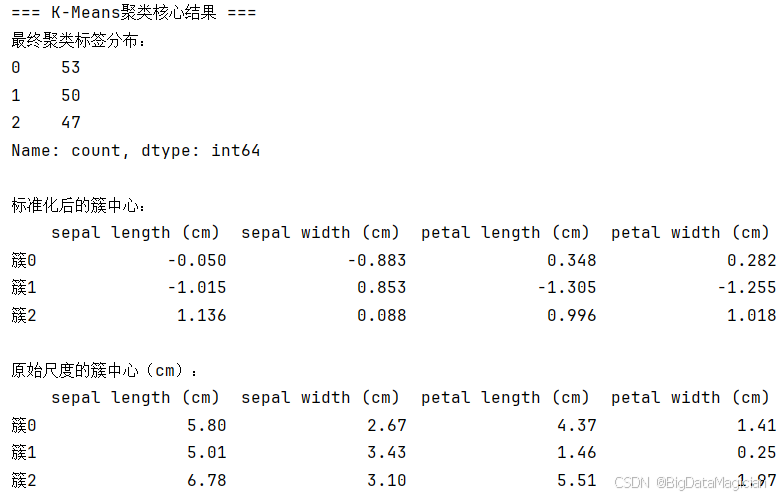
print(cluster_centers_original.round(2))聚类标签分布:最终聚类标签(0/1/2)的样本数量分布相对均衡,簇0包含53个样本、簇1包含50个样本、簇2包含47个样本,无极端不平衡的簇划分,说明聚类结果的样本分布较为合理。
簇中心解读 :簇中心是每个簇的"代表样本",分别提供标准化与原始尺度两种形式(原始尺度更贴合业务认知)。标准化后的簇中心 体现各特征在簇内的相对偏离程度(如簇1的花瓣长度、宽度标准化值均接近-1.3,远低于均值;簇2的花瓣长度、宽度标准化值接近1.0,远高于均值);原始尺度的簇中心(单位:cm) 中,簇1的花萼宽度(3.43)最大,花瓣长度(1.46)、宽度(0.25)最小,对应"山鸢尾"的形态特征;簇2的花萼长度(6.78)、花瓣长度(5.51)、花瓣宽度(1.97)均最大,对应"维吉尼亚鸢尾"的形态特征;簇0的各特征数值介于簇1与簇2之间,对应"变色鸢尾"的形态特征。
这一结果与鸢尾花的实际品种形态规律高度一致,说明K-Means模型成功捕捉到了数据的天然群体划分。
6. 模型评估
K-Means聚类为无监督学习,评估需结合"量化指标(簇内紧凑度+簇间分离度)""真实标签匹配度""可视化验证"三个维度,全面验证聚类效果的合理性。
6.1 核心评估指标
通过惯性值、轮廓系数、DBI指数、CHI指数四个指标,从"簇内紧凑度""综合质量""簇间分离度""方差占比"四个维度全面评估K-Means聚类结果的质量。
- 惯性值(Inertia):簇内紧凑度,值越小越好;
- 轮廓系数(Silhouette Score):综合簇内紧凑度与簇间分离度,越接近1越好;
- 戴维斯-布尔丁指数(DBI):簇间分离度与簇内紧凑度的比值,值越小越好;
- 卡尔斯基-哈拉巴斯指数(CHI):簇间方差与簇内方差的比值,值越大越好。
python
# ====================核心评估指标====================
from sklearn.metrics import silhouette_score, davies_bouldin_score, calinski_harabasz_score
print("=== 核心评估指标 ===")
# 计算核心量化指标
print(f"惯性值(簇内紧凑度): {round(inertia, 2)}")
print(f"轮廓系数(综合质量): {round(silhouette_score(X_scaled, cluster_labels), 3)}")
print(f"DBI指数(簇间分离度): {round(davies_bouldin_score(X_scaled, cluster_labels), 3)}")
print(f"CHI指数(簇间/簇内方差比): {round(calinski_harabasz_score(X_scaled, cluster_labels), 2)}")- 惯性值(139.82):代表簇内所有样本到其簇中心的距离平方和,该值处于合理区间(结合k=3的肘部法则结果),说明簇内样本的紧凑度较好;
- 轮廓系数(0.46):处于[0,1]区间的中等水平,既体现了簇内样本的紧凑性,也保证了簇间的区分度,符合聚类任务的预期质量;
- DBI指数(0.834):该指数越小代表簇间分离度越好,0.834的数值说明各簇之间的重叠程度较低,划分边界清晰;
- CHI指数(241.9):代表簇间方差与簇内方差的比值,值越大说明簇间差异越显著,241.9的高数值进一步验证了聚类结果的有效性。
综合来看,这组指标共同表明本次K-Means聚类(k=3)的结果既保证了簇内样本的聚集性,又实现了簇间样本的区分度,整体聚类质量良好。

6.2 聚类结果可视化
6.2.1 聚类标签分布可视化
聚类标签分布可反映各簇的样本数量均衡性,是评估聚类结果合理性的基础指标之一。本次通过柱状图展示3个簇的样本数量分布。
python
# ====================聚类标签分布可视化====================
df_cluster_labels = pd.Series(cluster_labels).value_counts().reset_index()
df_cluster_labels.columns = ['类别', '数量']
df_cluster_labels['类别'] = df_cluster_labels['类别'].map({
0: '簇1',
1: '簇2',
2: '簇3'
})
print("\n聚类标签分布:")
print(df_cluster_labels)
plt.figure(figsize=(6, 4))
sns.barplot(x='类别', hue='类别', y='数量', data=df_cluster_labels, palette='Set3')
for x, y in zip(df_cluster_labels['类别'], df_cluster_labels['数量']):
plt.text(x=x, y=y, s=y, ha='center', va='bottom')
plt.title('聚类标签分布')
plt.xlabel('类别')
plt.ylabel('数量')
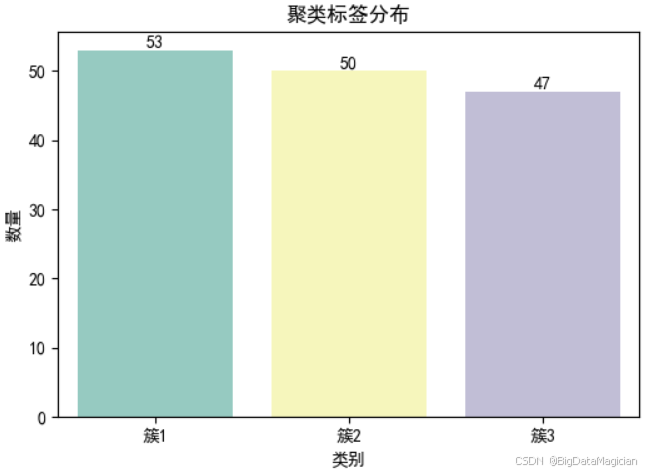
plt.savefig('./聚类标签分布柱状图.png')从图中可见,簇1包含53个样本、簇2包含50个样本、簇3包含47个样本------各簇的样本数量差异较小(最大差值仅6个),分布相对均衡,无"簇样本量极少/极多"的极端情况。这种均衡的分布说明K-Means聚类(k=3)未出现"簇划分偏向某一群体"的问题,进一步验证了聚类结果的稳定性与合理性。
6.2.2 聚类效果可视化
采用散点图矩阵(Pairplot)结合对角线核密度图,从"特征两两组合+单特征分布"双维度直观展示聚类效果,不同颜色代表不同簇。
python
# ====================聚类效果可视化散点图====================
plt.figure(figsize=(8, 8))
feature_names = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)', 'cluster_label']
# 绘制所有特征的散点图矩阵
sns.pairplot(
data=df_iris_scaled[feature_names],
hue='cluster_label',
palette='Set2',
corner=True, # 只显示下三角,避免重复
diag_kind='kde' # 对角线用核密度图
)
plt.tight_layout()
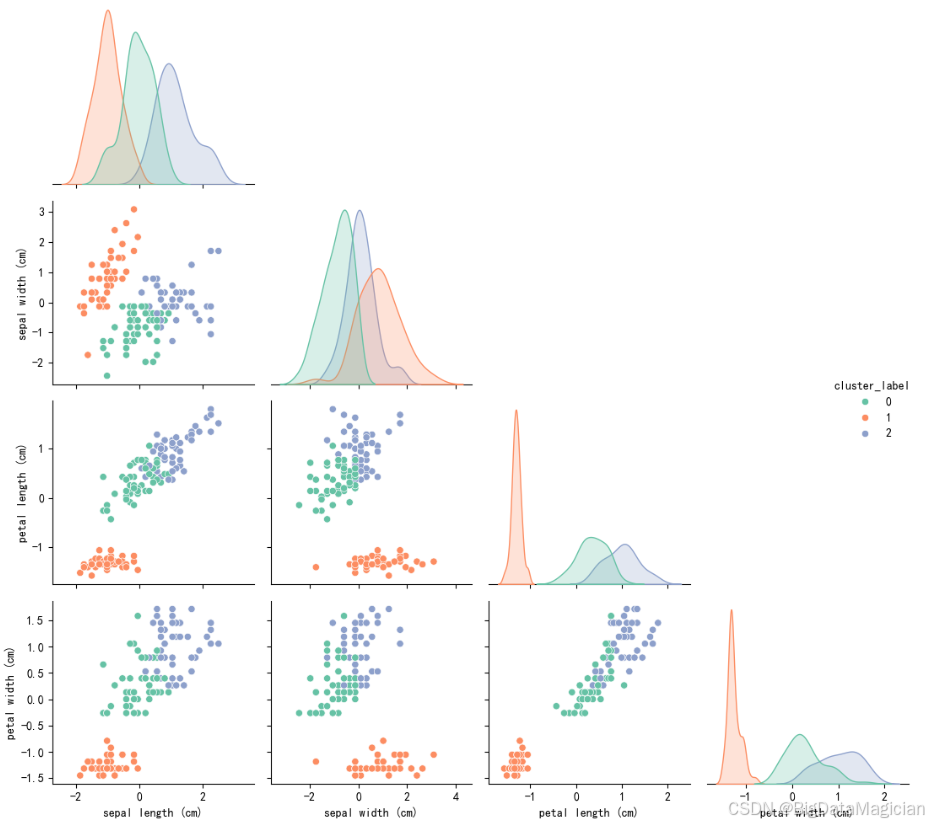
plt.savefig('KMeans聚类效果散点图.png')- 散点图区域(下三角):不同簇的样本在特征组合下呈现明显的聚集性------以"花瓣长度-花瓣宽度"组合为例,橙色样本(簇1)集中在左下角、青色样本(簇0)集中在中间区域、蓝色样本(簇2)集中在右上角,三类几乎无重叠,体现了簇间的强区分度;
- 核密度图区域(对角线):各簇的单特征分布边界清晰(如花瓣长度的核密度图呈现三个独立峰值),与聚类前的单特征分布规律一致,验证了簇内样本的紧凑性。
这一可视化结果直观印证了K-Means聚类的有效性,样本按形态特征自然划分为三个独立群体,与鸢尾花的实际品种分类高度契合。
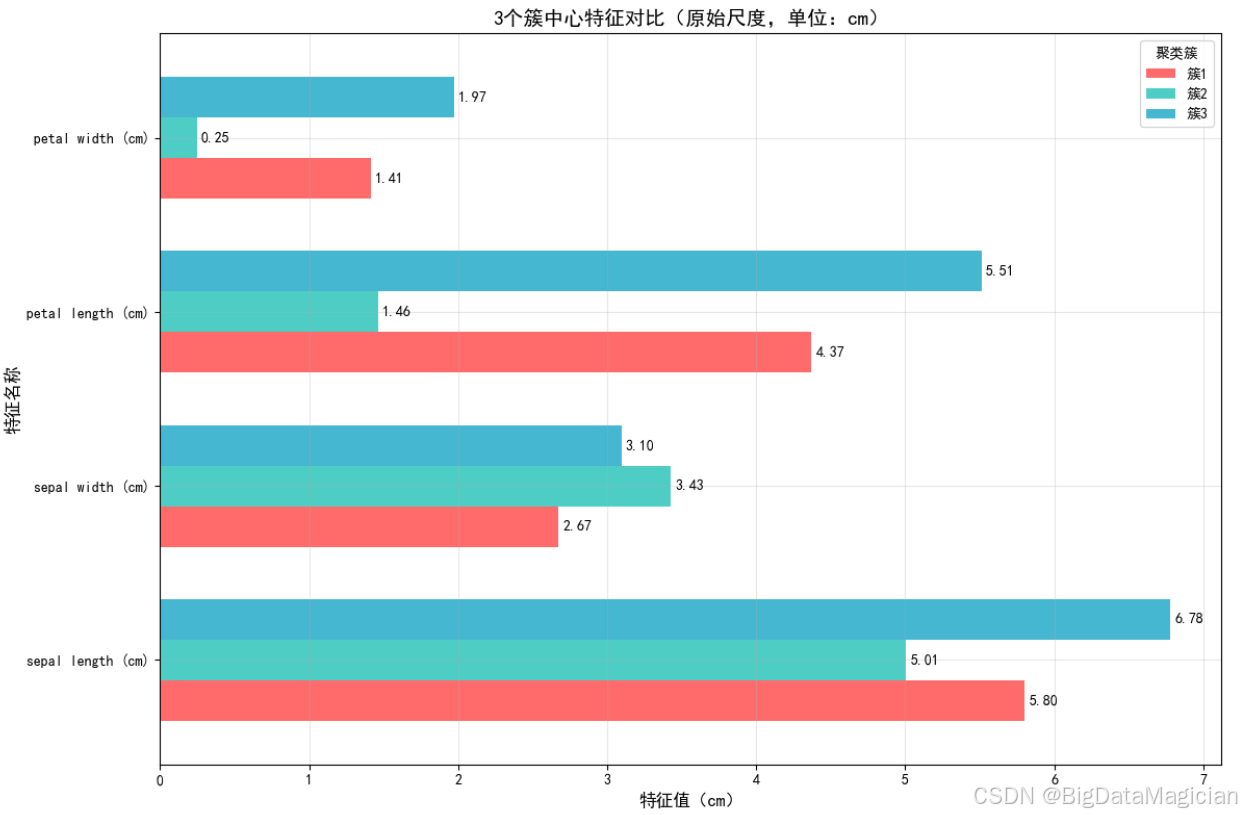
6.2.3 原始尺度的簇中心可视化
为更直观地对比不同簇的形态特征差异,将3个簇的原始尺度中心以水平柱状图展示(不同颜色代表不同簇),并标注具体特征数值。
python
# ====================原始尺度的簇中心可视化====================
import numpy as np
# 簇中心特征柱状图(原始尺度)
plt.figure(figsize=(12, 8))
ax = cluster_centers_original.T.plot(
kind='barh',
color=['#FF6B6B', '#4ECDC4', '#45B7D1'],
width=0.7,
figsize=(12, 8)
)
# 添加数值文本注释
for container in ax.containers:
ax.bar_label(container, fmt='%.2f', padding=3, fontsize=10)
plt.title('3个簇中心特征对比(原始尺度,单位:cm)', fontsize=14, fontweight='bold')
plt.xlabel('特征值(cm)', fontsize=12)
plt.ylabel('特征名称', fontsize=12)
plt.legend(title='聚类簇', loc='upper right')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.savefig('簇中心特征对比条形图.png')从图中可清晰区分各簇的核心形态特征:
- 簇2(青绿色):花萼宽度(3.43cm)显著大于另外两个簇,花瓣长度(1.46cm)、花瓣宽度(0.25cm)为三者中最小,对应"山鸢尾"的紧凑花瓣特征;
- 簇3(浅蓝色):花萼长度(6.78cm)、花瓣长度(5.51cm)、花瓣宽度(1.97cm)均为三者中最大,对应"维吉尼亚鸢尾"的舒展花部形态;
- 簇1(红色):所有特征数值均介于簇2与簇3之间(如花瓣长度4.37cm、花瓣宽度1.41cm),对应"变色鸢尾"的过渡形态特征。
这种特征差异与鸢尾花实际品种的形态规律完全吻合,直观验证了K-Means聚类结果的合理性------簇的划分准确捕捉了不同品种鸢尾花的核心形态差异。
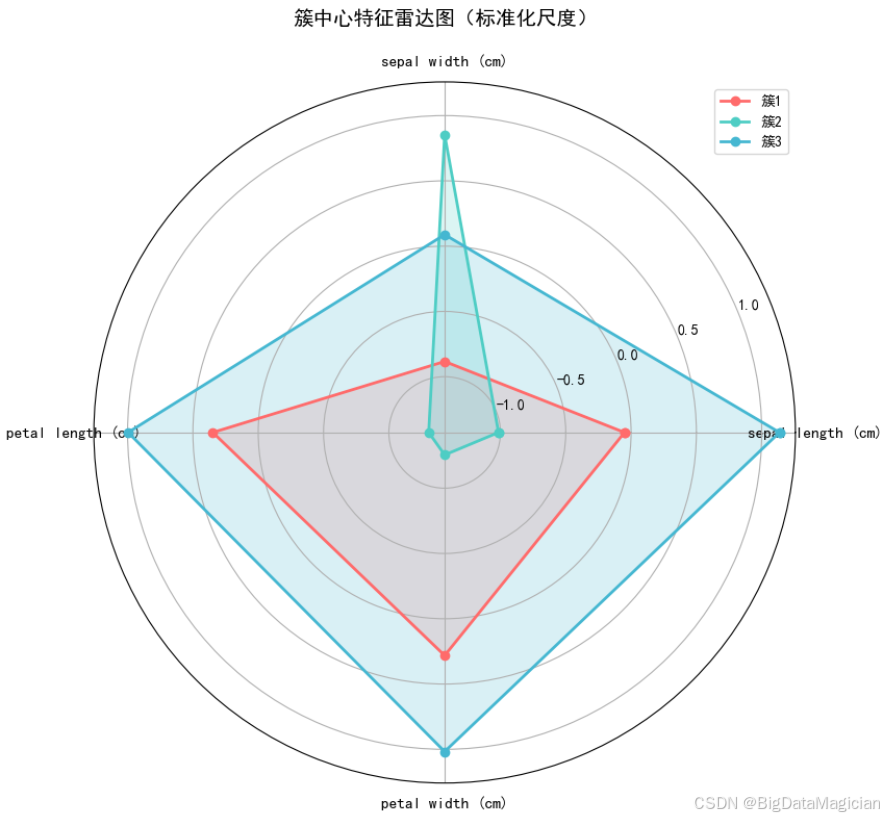
6.2.4 标准化后的簇中心可视化
为消除特征尺度差异的干扰,采用雷达图展示标准化后的簇中心特征,更直观地对比各簇在不同特征维度上的相对差异(雷达图的径向距离代表特征偏离均值的程度)。
python
# ====================标准化后的簇中心可视化====================
# 簇中心特征雷达图(标准化尺度,消除量纲影响)
plt.figure(figsize=(10, 8))
# 标准化后的簇中心数据
centers_scaled = cluster_centers
# 特征名称
features = df_iris.columns[:-2]
# 雷达图角度设置
angles = np.linspace(start=0, stop=2 * np.pi, num=len(features), endpoint=False).tolist()
angles += angles[:1] # 闭合雷达图
# 循环绘制每个簇的雷达图
colors = ['#FF6B6B', '#4ECDC4', '#45B7D1']
for i, (center, color) in enumerate(zip(centers_scaled, colors)):
values = center.tolist()
values += values[:1] # 闭合数据
plt.polar(angles, values, label=f'簇{i + 1}', color=color, linewidth=2, marker='o')
plt.fill(angles, values, color=color, alpha=0.2)
# 调整雷达图样式
plt.xticks(ticks=angles[:-1], labels=features, fontsize=11)
# plt.yticks([]) # 隐藏径向刻度
plt.title('簇中心特征雷达图(标准化尺度)', fontsize=14, pad=20)
plt.legend()
plt.tight_layout()
plt.savefig('簇中心特征雷达图.png')从图中可观察到各簇的"特征轮廓"差异显著:
- 簇2(青绿色):在"花萼宽度"维度显著向外延伸(偏离均值最多),但在"花瓣长度""花瓣宽度"维度明显向内收缩(远低于均值),形成了"宽萼片+窄花瓣"的特征轮廓;
- 簇3(浅蓝色):在"花萼长度""花瓣长度""花瓣宽度"维度均大幅向外延伸,是所有簇中特征值整体偏高的簇,对应"大尺寸花部"的轮廓;
- 簇1(红色):各特征维度的径向距离均介于簇2与簇3之间,呈现"中等尺寸花部"的均衡轮廓。
这种标准化后的特征轮廓差异,进一步验证了K-Means聚类对不同鸢尾花群体的区分能力------各簇的特征组合模式清晰,聚类结果的簇间区分度较高。
五、完整代码
1. 完整代码
python
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.datasets import load_iris
# 设置中文字体正常显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置Pandas全局选项
pd.set_option('display.max_columns', None)
pd.set_option('display.width', None)
pd.set_option('display.max_colwidth', 50)
pd.set_option('display.expand_frame_repr', False)
# ====================加载数据====================
# 加载鸢尾花数据集
iris = load_iris()
# 转换为DataFrame
df_iris = pd.DataFrame(
data=iris.data, # 特征矩阵
columns=iris.feature_names # 特征名称
)
# 添加真实品种标签列(用于后续对比聚类结果)
df_iris['species'] = iris.target
# 将数字标签映射为品种名称(提升可读性)
df_iris['species_name'] = (df_iris['species'].map({
0: '山鸢尾',
1: '变色鸢尾',
2: '维吉尼亚鸢尾'
}))
# ====================探索性数据分析====================
# ====================数据基本信息====================
# 基础信息探索
print("=== 鸢尾花数据集基础信息 ===")
print(f"数据集形状:{df_iris.shape}(样本数×特征数)")
print("\n=== 数据前5行预览 ===")
print(df_iris.head())
print("\n=== 数据类型与缺失值检查 ===")
print(df_iris.info()) # 无缺失值,特征均为浮点型
print("\n=== 特征统计描述 ===")
print(df_iris.describe().round(2)) # 查看特征的均值、标准差等
print("\n=== 各品种样本数量分布 ===")
print(df_iris['species_name'].value_counts())
# ====================单特征分布分析====================
import matplotlib.pyplot as plt
import seaborn as sns
# 绘制核密度图,KDE:核密度估计
plt.figure(figsize=(15, 10))
feature = df_iris.columns[:-2]
for i in range(len(feature)):
plt.subplot(2, 2, i + 1)
sns.kdeplot(
data=df_iris,
x=feature[i],
fill=True,
common_norm=False, # 每个类别单独归一化
alpha=0.5
)
plt.title(f'按类别的 {feature[i]} 核密度估计图')
plt.xlabel(feature[i])
plt.tight_layout()
plt.savefig('单特征分布核密度估计图.png')
# ===================特征间相关性分析====================
import matplotlib.pyplot as plt
import seaborn as sns
features = df_iris.columns[:-2]
# 全局特征相关性热力图(不区分品种)
plt.figure(figsize=(10, 8))
# 计算特征间的皮尔逊相关系数
corr_matrix = df_iris[features].corr(method='spearman')
# 绘制热力图
mask = np.triu(m=np.ones_like(corr_matrix, dtype=bool), k=1) # 隐藏上三角(避免重复)
sns.heatmap(data=corr_matrix, mask=mask, annot=True, fmt='.2f', cmap='coolwarm', linewidths=0.5)
plt.title('鸢尾花特征相关性热力图', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.savefig('特征间相关性.png')
# ===================特征变异系数分析====================
# 计算各特征的变异系数(反映离散程度,变异系数=标准差/均值)
cv_data = []
for feat in df_iris.columns[:-2]:
cv = df_iris[feat].std() / df_iris[feat].mean()
cv_data.append({'特征': feat, '变异系数': round(cv, 3)})
cv_df = pd.DataFrame(cv_data).sort_values('变异系数', ascending=False)
print("各特征变异系数(离散程度):")
print(cv_df)
plt.figure(figsize=(8, 5))
sns.barplot(data=cv_df, x='变异系数', y='特征', hue='特征', palette='viridis')
# 添加数值标签
for index, value in enumerate(cv_df['变异系数']):
plt.text(x=value + 0.001, y=index, s=value)
plt.title('各特征的变异系数(CV = 标准差 / 均值)')
plt.xlabel('变异系数')
plt.ylabel('特征')
plt.tight_layout()
plt.savefig('变异系数条形图.png')
# ====================异常值检测与处理====================
import seaborn as sns
import matplotlib.pyplot as plt
# 提取4个形态特征
features = df_iris.columns[:-2]
# 绘制箱线图检测异常值
plt.figure(figsize=(12, 8))
for i, feat in enumerate(features):
plt.subplot(2, 2, i + 1)
sns.boxplot(data=df_iris, y=feat, color='lightblue')
plt.title(f'{feat} 箱线图(异常值检测)')
plt.xlabel(feat)
plt.tight_layout()
plt.savefig('特征箱线图_异常值检测.png')
# 定量计算异常值数量
outlier_info = {}
for feat in features:
# 计算四分位数和IQR
Q1 = df_iris[feat].quantile(0.25)
Q3 = df_iris[feat].quantile(0.75)
IQR = Q3 - Q1
# 异常值判定条件
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
# 统计异常值数量
outliers = df_iris[(df_iris[feat] < lower_bound) | (df_iris[feat] > upper_bound)]
outlier_info[feat] = {
'下界': round(lower_bound, 2),
'上界': round(upper_bound, 2),
'异常值数量': len(outliers),
'异常值占比': f'{round(len(outliers) / len(df_iris) * 100, 2)}%'
}
# 输出异常值统计结果
outlier_df = pd.DataFrame(outlier_info).T
print("=== 各特征异常值统计 ===")
print(outlier_df)
# ====================特征标准化====================
from sklearn.preprocessing import StandardScaler
# 提取特征矩阵(仅保留4个形态特征)
X = df_iris[features].values
# 初始化标准化器
scaler = StandardScaler()
# 拟合并转换数据
X_scaled = scaler.fit_transform(X)
# 将标准化后的数据转换为DataFrame,便于后续分析
df_iris_scaled = pd.DataFrame(
X_scaled,
columns=features
)
# 保留标签列(用于后续对比聚类结果)
df_iris_scaled['species'] = df_iris['species']
df_iris_scaled['species_name'] = df_iris['species_name']
# 验证标准化效果
print("标准化后特征统计:")
print(df_iris_scaled[features].describe().T.round(2))
# ====================肘部法和轮廓系数法则确定最优k值====================
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score
# 测试k值范围:2~10
k_range = range(2, 11)
# 存储不同k值的惯性值
inertias = []
# 存储不同k值的轮廓系数
sil_scores = []
for k in k_range:
kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
kmeans.fit(X_scaled)
inertias.append(kmeans.inertia_)
labels = kmeans.predict(X_scaled)
sil_score = silhouette_score(X_scaled, labels)
sil_scores.append(sil_score)
df_k = pd.DataFrame({
'k': k_range,
'惯性值': inertias,
'轮廓系数': sil_scores
})
print(f"各k值对应的惯性值和轮廓系数:\n{df_k}")
# 绘制肘部法则图
plt.figure(figsize=(14, 5))
plt.subplot(1, 2, 1)
plt.plot(k_range, inertias, 'o-', color='#2E86AB', linewidth=2, markersize=8)
for x, y in zip(k_range, inertias):
plt.text(x=x, y=y + 3, s=f'{y:.2f}')
plt.title('K-Means肘部法则图(惯性值 vs k值)')
plt.xlabel('聚类数k', fontsize=12)
plt.ylabel('惯性值(Inertia)', fontsize=12)
plt.xticks(k_range)
plt.grid(alpha=0.3)
# 绘制轮廓系数曲线
plt.subplot(1, 2, 2)
plt.plot(k_range, sil_scores, 'o-', color='#F18F01', linewidth=2, markersize=8)
for x, y in zip(k_range, sil_scores):
plt.text(x=x, y=y + 0.01, s=f'{y:.3f}', ha='center')
plt.title('K-Means轮廓系数图(轮廓系数 vs k值)', fontsize=14, fontweight='bold')
plt.xlabel('聚类数k', fontsize=12)
plt.ylabel('轮廓系数(Silhouette Score)', fontsize=12)
plt.xticks(k_range)
plt.grid(alpha=0.3)
plt.savefig('KMeans肘部法则图和轮廓系数图.png')
# ====================K-Means模型训练====================
from sklearn.cluster import KMeans
# 初始化K-Means模型(最优k=3)
kmeans = KMeans(n_clusters=3, random_state=42, n_init=10)
# 训练模型(输入标准化后的特征矩阵)
kmeans.fit(X_scaled)
# 获取聚类核心结果
cluster_labels = kmeans.labels_ # 所有样本的聚类标签(0/1/2)
cluster_centers = kmeans.cluster_centers_ # 3个簇的中心(标准化后,维度:3×4)
inertia = kmeans.inertia_ # 最终惯性值(簇内紧凑度指标)
# 将聚类标签合并到预处理后的DataFrame,便于后续分析
df_iris_scaled['cluster_label'] = cluster_labels
df_iris_scaled.to_csv('标准化后的聚类结果.csv', index=False)
df_iris_new = df_iris.copy()
df_iris_new['cluster_label'] = cluster_labels
df_iris_new.to_csv('原始数据的聚类结果.csv', index=False)
# 输出训练结果摘要
print("=== K-Means模型训练结果 ===")
print(f"最终聚类标签分布:\n{pd.Series(cluster_labels).value_counts().sort_index()}")
print(f"\n模型最终惯性值:{inertia:.2f}")
print(f"\n标准化后的簇中心:")
cluster_centers_scaled = pd.DataFrame(
cluster_centers,
columns=df_iris.columns[:-2], # 特征名称
index=[f'簇{i + 1}' for i in range(3)] # 簇名称
)
print(cluster_centers_scaled.round(3))
# 簇中心逆标准化(还原为原始尺度cm,便于业务解读)
cluster_centers_original = scaler.inverse_transform(cluster_centers)
cluster_centers_original = pd.DataFrame(
cluster_centers_original,
columns=df_iris.columns[:-2],
index=[f'簇{i + 1}' for i in range(3)]
)
print(f"\n原始尺度的簇中心(单位:cm):")
print(cluster_centers_original.round(2))
# ====================核心评估指标====================
from sklearn.metrics import silhouette_score, davies_bouldin_score, calinski_harabasz_score
print("=== 核心评估指标 ===")
# 计算核心量化指标
print(f"惯性值(簇内紧凑度): {round(inertia, 2)}")
print(f"轮廓系数(综合质量): {round(silhouette_score(X_scaled, cluster_labels), 3)}")
print(f"DBI指数(簇间分离度): {round(davies_bouldin_score(X_scaled, cluster_labels), 3)}")
print(f"CHI指数(簇间/簇内方差比): {round(calinski_harabasz_score(X_scaled, cluster_labels), 2)}")
# ====================聚类标签分布可视化====================
df_cluster_labels = pd.Series(cluster_labels).value_counts().reset_index()
df_cluster_labels.columns = ['类别', '数量']
df_cluster_labels['类别'] = df_cluster_labels['类别'].map({
0: '簇1',
1: '簇2',
2: '簇3'
})
print("\n聚类标签分布:")
print(df_cluster_labels)
plt.figure(figsize=(6, 4))
sns.barplot(x='类别', hue='类别', y='数量', data=df_cluster_labels, palette='Set3')
for x, y in zip(df_cluster_labels['类别'], df_cluster_labels['数量']):
plt.text(x=x, y=y, s=y, ha='center', va='bottom')
plt.title('聚类标签分布')
plt.xlabel('类别')
plt.ylabel('数量')
plt.savefig('./聚类标签分布柱状图.png')
# ====================聚类效果可视化散点图====================
plt.figure(figsize=(8, 8))
feature_names = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)', 'cluster_label']
# 绘制所有特征的散点图矩阵(快速查看多特征关系)
sns.pairplot(
data=df_iris_scaled[feature_names],
hue='cluster_label',
palette='Set2',
corner=True, # 只显示下三角,避免重复
diag_kind='kde' # 对角线用核密度图
)
plt.tight_layout()
plt.savefig('KMeans聚类效果散点图.png')
# ====================原始尺度的簇中心可视化====================
import numpy as np
# 簇中心特征柱状图(原始尺度)
plt.figure(figsize=(12, 8))
ax = cluster_centers_original.T.plot(
kind='barh',
color=['#FF6B6B', '#4ECDC4', '#45B7D1'],
width=0.7,
figsize=(12, 8)
)
# 添加数值文本注释
for container in ax.containers:
ax.bar_label(container, fmt='%.2f', padding=3, fontsize=10)
plt.title('3个簇中心特征对比(原始尺度,单位:cm)', fontsize=14, fontweight='bold')
plt.xlabel('特征值(cm)', fontsize=12)
plt.ylabel('特征名称', fontsize=12)
plt.legend(title='聚类簇', loc='upper right')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.savefig('簇中心特征对比条形图.png')
# ====================标准化后的簇中心可视化====================
# 簇中心特征雷达图(标准化尺度,消除量纲影响)
plt.figure(figsize=(10, 8))
# 标准化后的簇中心数据
centers_scaled = cluster_centers
# 特征名称
features = df_iris.columns[:-2]
# 雷达图角度设置
angles = np.linspace(start=0, stop=2 * np.pi, num=len(features), endpoint=False).tolist()
angles += angles[:1] # 闭合雷达图
# 循环绘制每个簇的雷达图
colors = ['#FF6B6B', '#4ECDC4', '#45B7D1']
for i, (center, color) in enumerate(zip(centers_scaled, colors)):
values = center.tolist()
values += values[:1] # 闭合数据
plt.polar(angles, values, label=f'簇{i + 1}', color=color, linewidth=2, marker='o')
plt.fill(angles, values, color=color, alpha=0.2)
# 调整雷达图样式
plt.xticks(ticks=angles[:-1], labels=features, fontsize=11)
# plt.yticks([]) # 隐藏径向刻度
plt.title('簇中心特征雷达图(标准化尺度)', fontsize=14, pad=20)
plt.legend()
plt.tight_layout()
plt.savefig('簇中心特征雷达图.png')