目录
- [1 二叉平衡树的概念](#1 二叉平衡树的概念)
- [2 二叉平衡树的结构](#2 二叉平衡树的结构)
- [3 二叉平衡树的插入](#3 二叉平衡树的插入)
-
- [3.1 插入](#3.1 插入)
- [3.2 旋转](#3.2 旋转)
-
- [3.2.1 右单旋](#3.2.1 右单旋)
- [3.2.2 左单旋](#3.2.2 左单旋)
- [3.2.3 右左双旋](#3.2.3 右左双旋)
- [3.2.4 左右双旋](#3.2.4 左右双旋)
- [4 二叉平衡树的查找](#4 二叉平衡树的查找)
- [5 二叉平衡树的代码](#5 二叉平衡树的代码)
1 二叉平衡树的概念
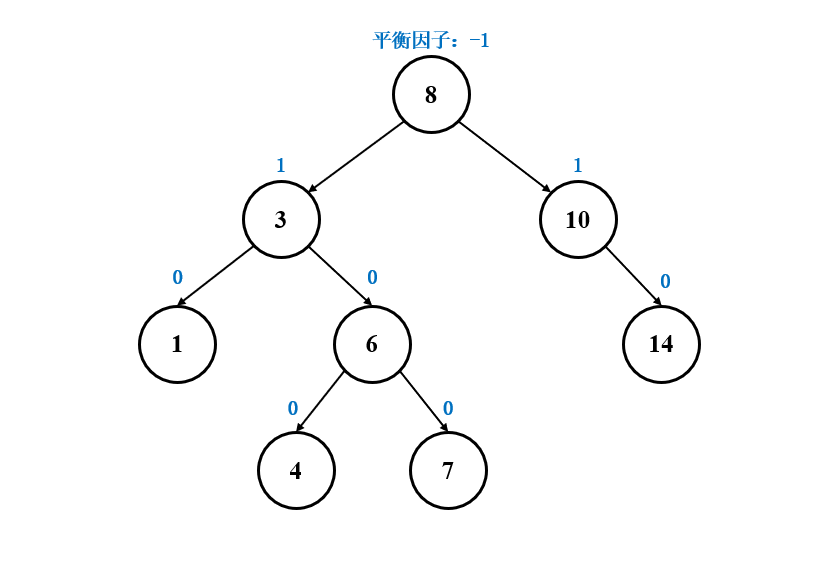
二叉平衡树,也叫 AVL 树,它的特性是树中的每个结点,左右子树高度差的绝对值不超过 1 ,它可以是一棵空树
在 AVL 树中,有个概念叫做平衡因子,它是一个结点左右子树高度的差,一般来说,如果一棵树是 AVL 树,那么它每个结点的平衡因子都不会超过 1,由于 AVL 树对平衡的限制,它的高度一般维持在 log2N 左右,所以它增删查的效率为 O(logN)
2 二叉平衡树的结构
二叉平衡树后续的操作需要找到父结点,所以在这里实现为三叉链的结构,加入平衡因子是为了通过平衡因子来判断是否平衡,维护二叉平衡树平衡的特性
cpp
//AVL树的结点
template<class K, class V>
class AVLTreeNode
{
pair<K, V> _kv; //存储的键值对
AVLTreeNode<K, V>* _left; //指向左孩子的指针
AVLTreeNode<K, V>* _right; //指向右孩子的指针
AVLTreeNode<K, V>* _parent; //指向父结点的指针
int _balanceFactor; //平衡因子
AVLTreeNode(const pair<K, V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_balanceFactor(0)
{}
};
//AVL树本体
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode Node;
public:
//...
private:
Node* _root; //根节点指针
};3 二叉平衡树的插入
3.1 插入
二叉平衡树在进行插入时,要按照 二叉排序树(BST) 的方式来进行插入,假设要插入的值为 x,当前结点的值为 val:
- x > val,向右子树移动来寻找插入点
- x < val,向左子树移动来寻找插入点
- x == val,由于有重复的值,所以不进行插入
当找到空结点时,将 x 插入至对应的位置
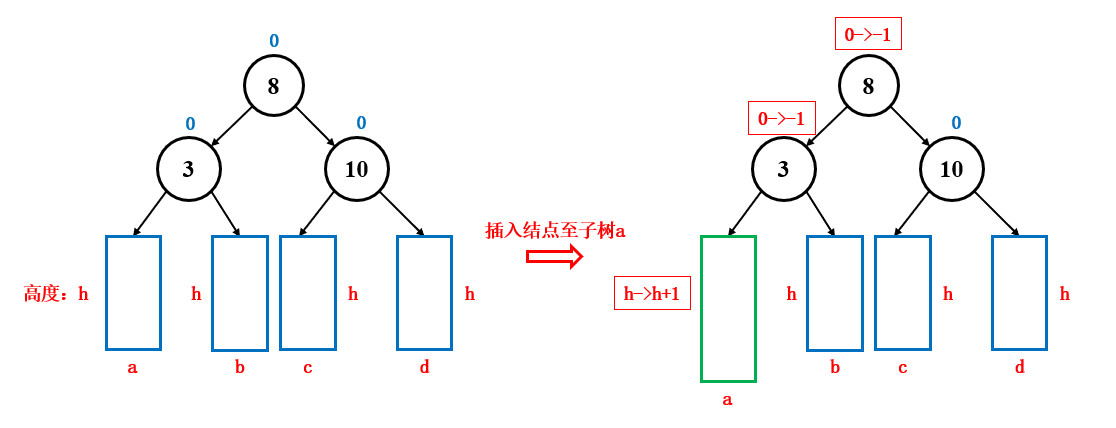
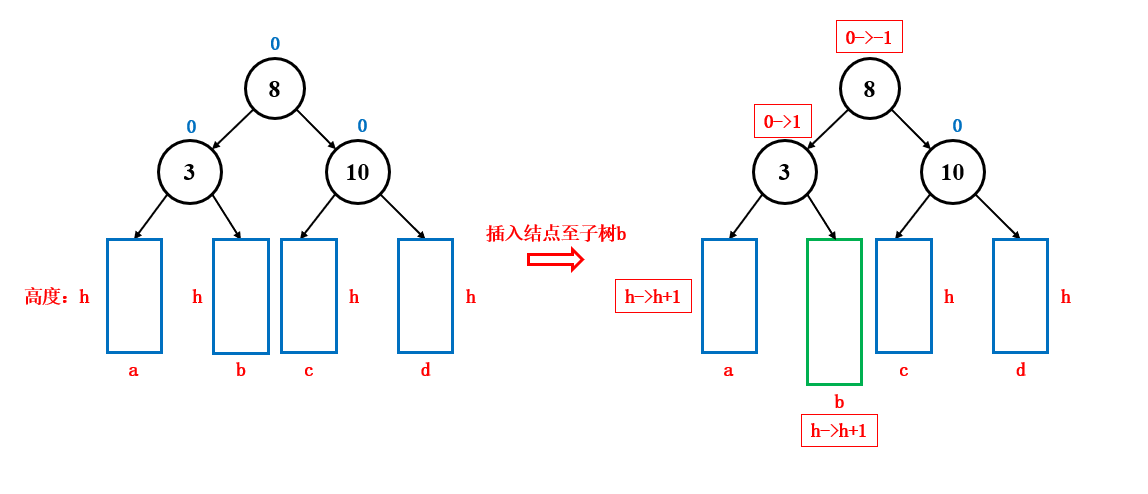
插入完成之后,由于子树中多了一个结点,所以要对父结点平衡因子进行修改,修改时,在这里采用右子树高度 - 左子树高度的方式:
- 左子树****中新增一个结点,左子树高度加一,右子树的高度不变,那么平衡因子就需要 减一
- 右子树****中新增一个结点,右子树高度加一,左子树的高度不变,那么平衡因子就需要 加一
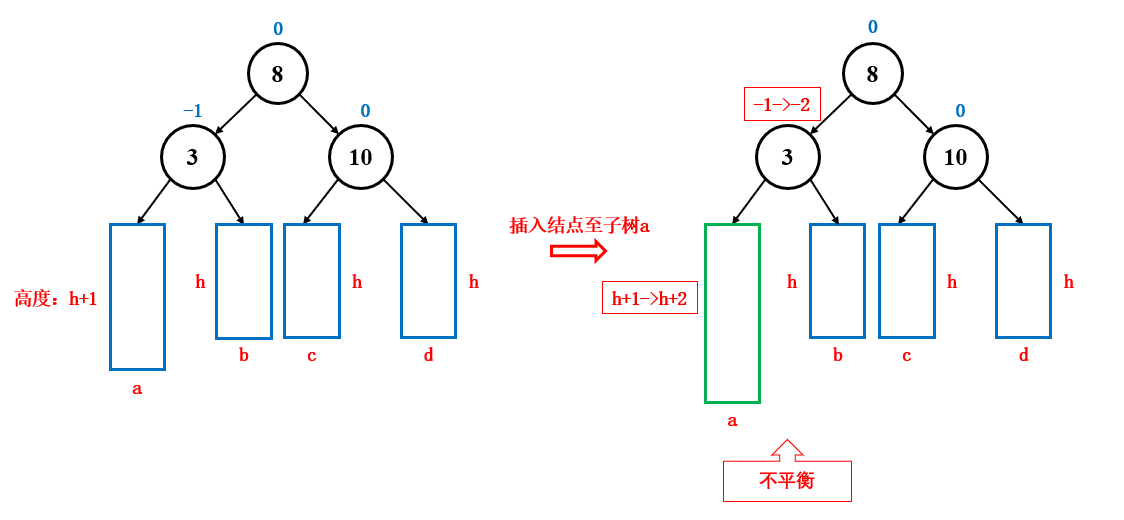
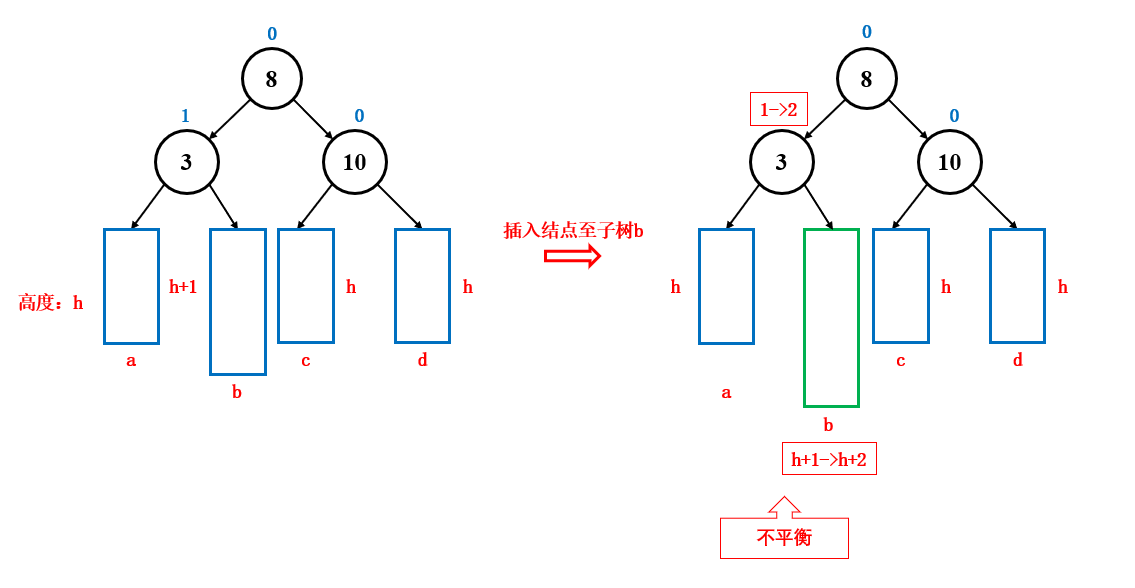
平衡因子的变化,会决定是否进行旋转,是否继续向上更新平衡因子:
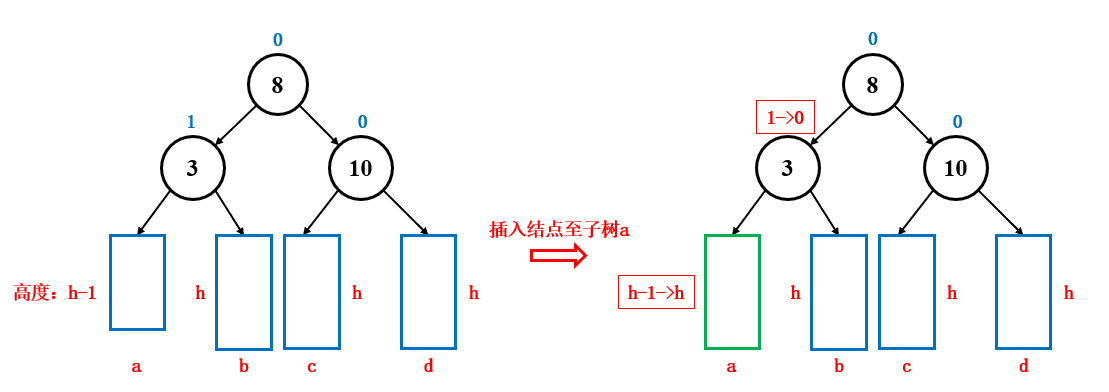
- 如果平衡因子变成了 0 ,说明原来的平衡因子是 1 或 -1 ,子树两边一高一低 ,此时插入了一个结点到左子树或右子树中,导致左子树或右子树高度加一,子树两边一样高,这个时候不会影响到更上层的父结点,所以不需要继续向上更新平衡因子
- 如果平衡因子变成了 1 或 -1 ,说明原来平衡因子是 0,子树两边一样高 ,此时插入了一个结点到左子树或右子树中,导致左子树或右子树高度加一,子树两边一高一低,那么会影响至更上层的父结点,所以还要向上更新,直到平衡因子为 0,最坏可能需要更新至根节点
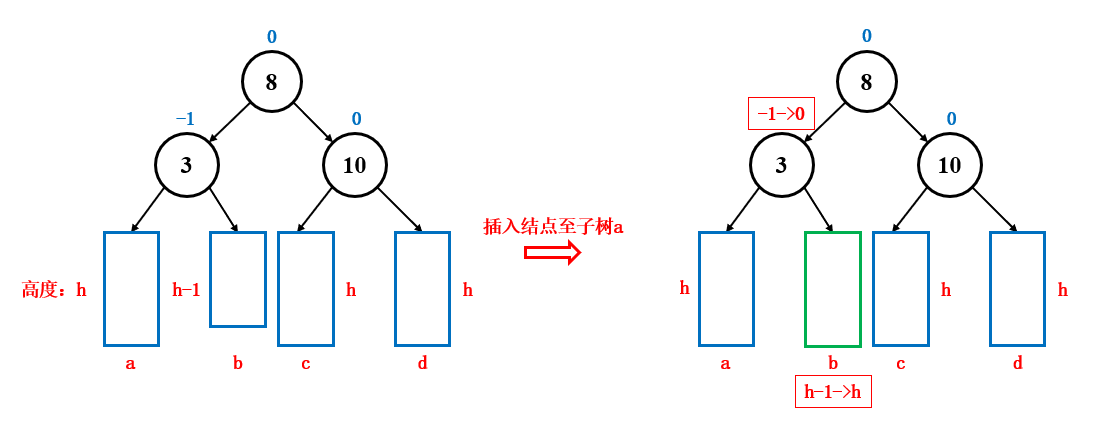
- 如果平衡因子变成了 2 或 -2 ,说明原来的平衡因子是 1 或 -1 ,子树两边一高一低 ,此时又往高的那一侧插入了一个结点,导致它变的更高了,这时候就发生了不平衡,需要进行旋转 ,通过旋转让子树恢复平衡,由于旋转较为复杂,所以在下面另起一个章节进行说明
插入实现(无旋转):
cpp
bool Insert(const pair<K, V>& kv)
{
if (!_root)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kv.first > cur->_kv.first) //大于向右子树移动
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first) //小于向左子树移动
{
parent = cur;
cur = cur->_left;
}
else //等于则不进行插入,去重
{
return false;
}
}
cur = new Node(kv);
cur->_parent = parent;
if (cur->_kv.first < parent->_kv.first) //在父结点的左子树中插入
{
parent->_left = cur;
}
else if (cur->_kv.first > parent->_kv.first) //在父结点的右子树中插入
{
parent->_right = cur;
}
while (parent)
{
//更新父结点的平衡因子
if (cur == parent->_left)
{
parent->_balanceFactor--;
}
else if (cur == parent->_right)
{
parent->_balanceFactor++;
}
if (parent->_balanceFactor == 0)
{
break;
}
else if (parent->_balanceFactor == 1 || parent->_balanceFactor == -1) //平衡因子是1或-1
{
//继续向上更新
cur = parent;
parent = parent->_parent;
}
else if (parent->_balanceFactor == 2 || parent->_balanceFactor == -2) //平衡因子是2或-2
{
//旋转
//...
}
}
return true;
}3.2 旋转
如果插入后,父结点的平衡因子是 2 或 -2,此时就要进行旋转操作,旋转主要有右单旋,左单旋,右左双旋和左右双旋四种情况,但是不管使用哪种旋转的方式,最终的目的都是使树恢复平衡
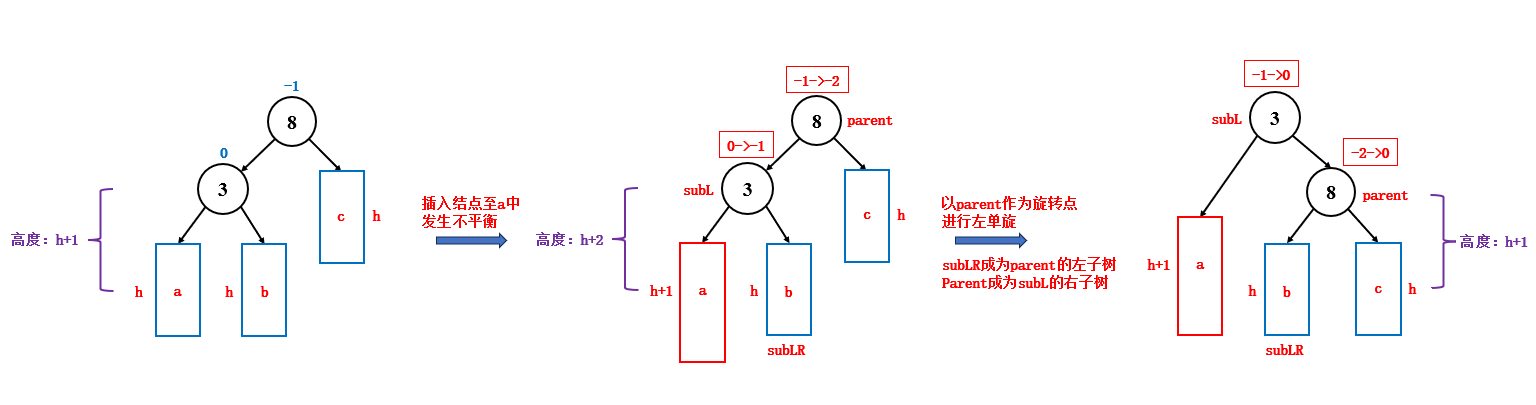
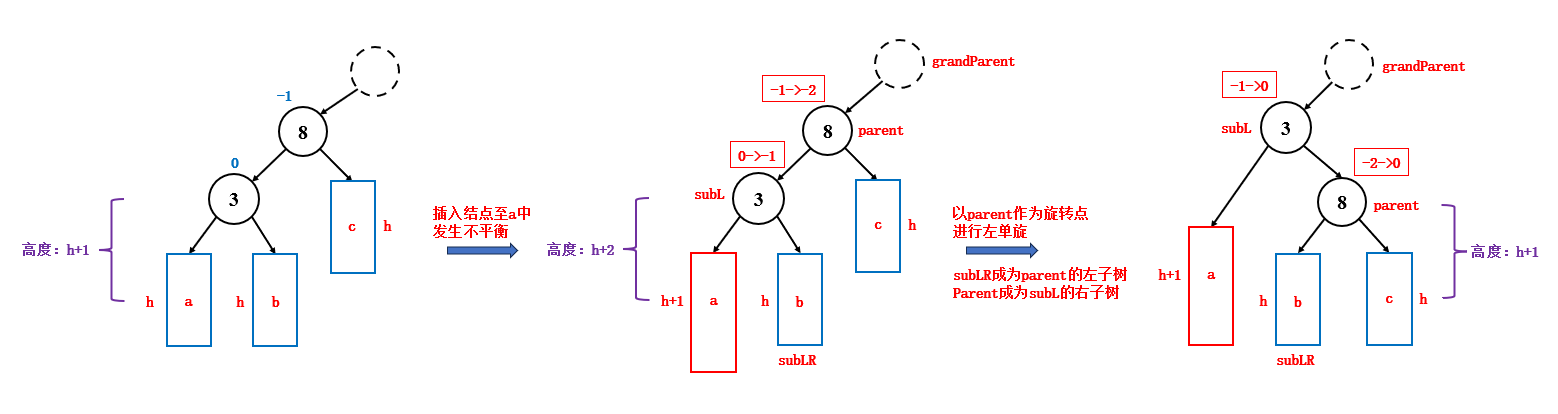
3.2.1 右单旋
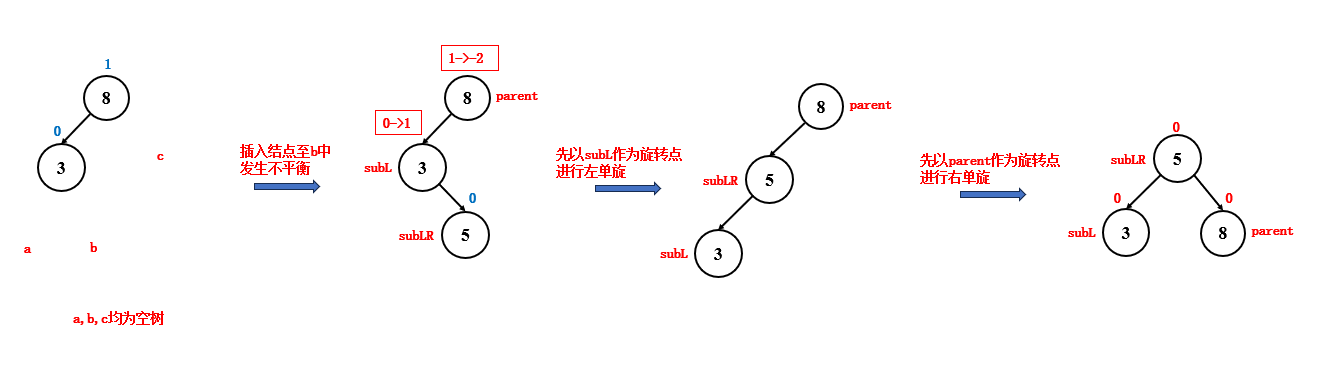
如果新插入的结点位于父结点左子树的左子树中,并且此时发生了不平衡,那么就说明,该子树太高了,此时要进行右单旋来调整平衡,右单旋时,结点的变化如下:
- 旋转时,如果 parent 是整棵树的根节点,那么旋转完成后,subL 会成为整棵树的根节点
- 旋转时,如果 parent 不是整棵树的根节点,而是当前子树的根节点,那么旋转完成后,subL 会成为新的子树的根节点,此时需要更改祖父结点 grandParent 的指向
- 旋转时,subLR 可能为空,所以需要进行判断,subLR 不为空,才更新它的父结点
右单旋代码实现:
cpp
//右单旋
void RotateToRight(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* grandParent = parent->_parent;
//更新子树
parent->_left = subLR;
subL->_right = parent;
parent->_parent = subL;
if (subLR)
subLR->_parent = parent;
if (parent == _root) //父结点是根节点,更新根节点
{
_root = subL;
subL->_parent = nullptr;
}
else //如果父结点不是根节点,那么要更新组父结点
{
subL->_parent = grandParent;
if (grandParent->_left == parent)
{
grandParent->_left = subL;
}
else if (grandParent->_right == parent)
{
grandParent->_right = subL;
}
}
//旋转后一定平衡,更新平衡因子
subL->_balanceFactor = 0;
parent->_balanceFactor = 0;
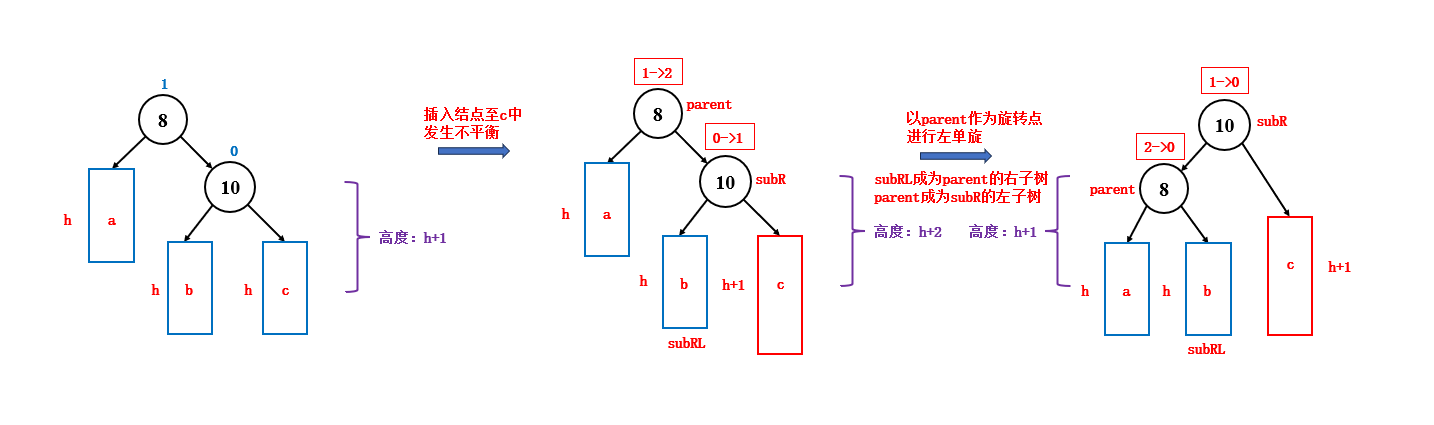
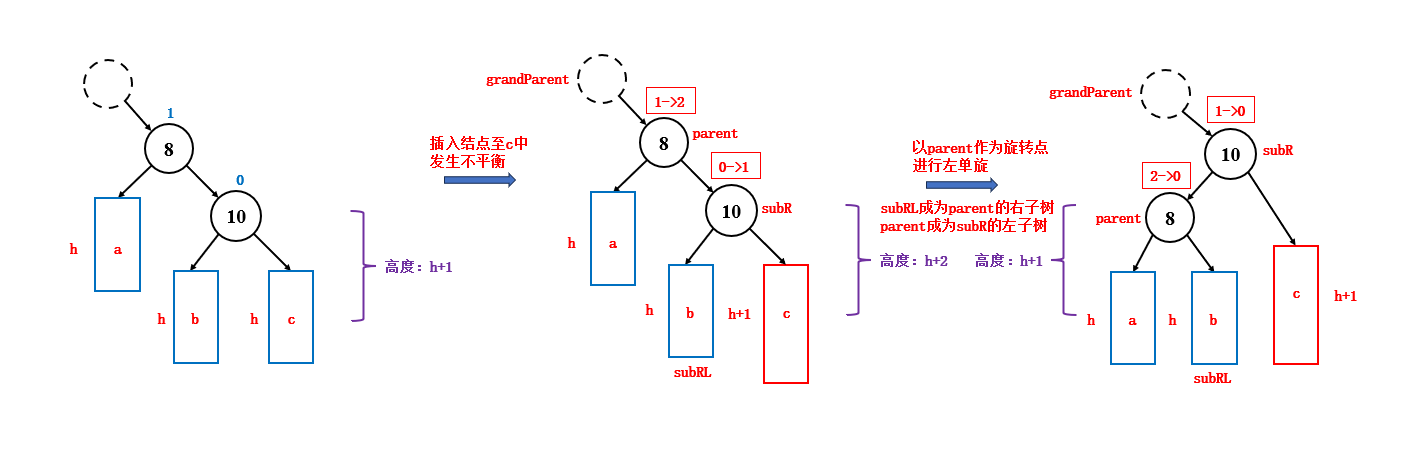
}3.2.2 左单旋
如果新插入的结点位于父结点右子树的右子树中,并且此时发生了不平衡,那么就说明,该子树太高了,此时要进行左单旋来调整平衡,左单旋时,结点的变化如下:
- 旋转时,如果 parent 是整棵树的根节点,那么旋转完成后,subR 会成为整棵树的根节点
- 旋转时,如果 parent 不是整棵树的根节点,而是当前子树的根节点,那么旋转完成后,subR 会成为新的子树的根节点,此时需要更改祖父结点 grandParent 的指向
- 旋转时,subRL 可能为空,所以需要进行判断,subRL 不为空,才更新它的父结点
左单旋代码实现:
cpp
//左单旋
void RotateToLeft(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* grandParent = parent->_parent;
//更新子树
subR->_left = parent;
parent->_right = subRL;
parent->_parent = subR;
if (subRL)
subRL->_parent = parent;
if (parent == _root) //父结点是根节点,更新根节点
{
_root = subR;
subR->_parent = nullptr;
}
else //如果父结点不是根节点,那么要更新组父结点
{
subR->_parent = grandParent;
if (grandParent->_left == parent)
{
grandParent->_left = subR;
}
else if (grandParent->_right == parent)
{
grandParent->_right = subR;
}
}
//旋转后一定平衡,更新平衡因子
subR->_balanceFactor = 0;
parent->_balanceFactor = 0;
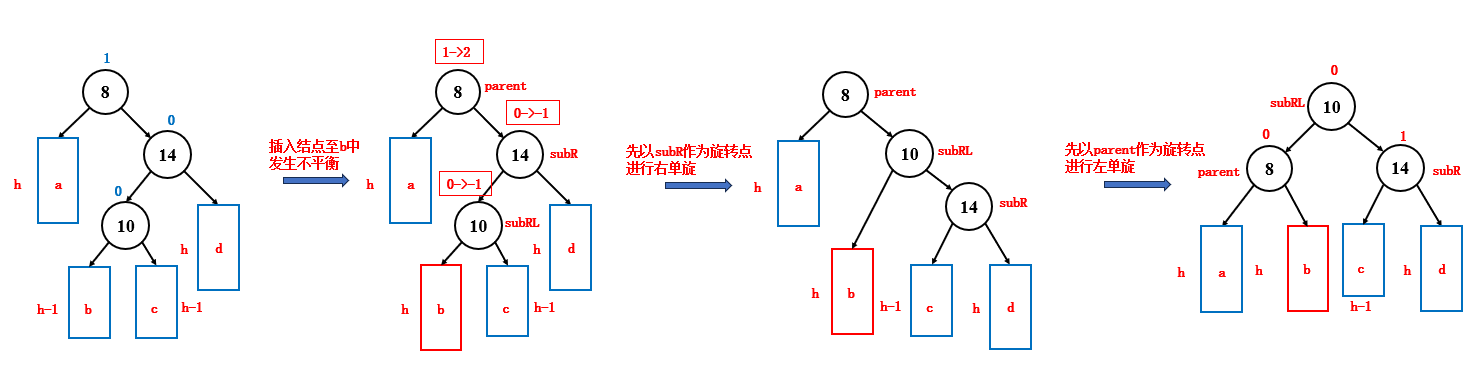
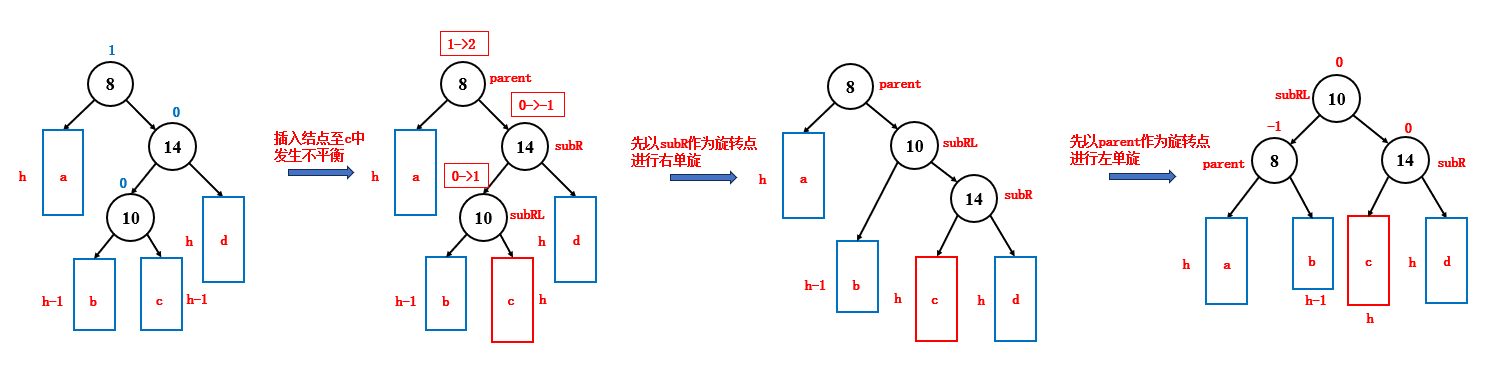
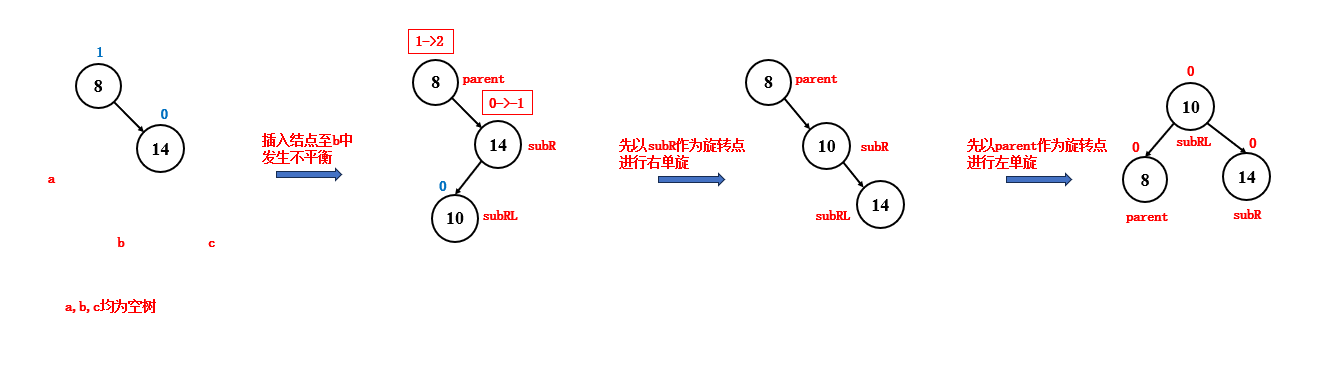
}3.2.3 右左双旋
如果新插入的结点位于父结点右子树的左子树中,并且此时发生了不平衡,就要进行右左双旋来调整平衡,右左双旋时,结点和平衡因子的变化如下:
subRL 的平衡因子,说明了新结点插入到了 b 中还是 c 中,会直接影响到最后 parent,subRL,subR 的平衡因子,因为 b 和 c 这两棵子树旋转后的位置是不一样的
- subRL 平衡因子为 -1,那么最后 parent 平衡因子为 0,subRL 平衡因子为1,subR 平衡因子为 0
- subRL 平衡因子为 1,那么最后 parent 平衡因子为 -1,subRL 平衡因子为 0,subR 平衡因子为 0
- subRL 平衡因子为 0,那么最后 parent 平衡因子为 0,subRL 平衡因子为 0,subR 平衡因子为 0
右左双旋代码实现:
cpp
//右左双旋
void RotateToRightThenToLeft(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int balanceFactor = subRL->_balanceFactor;
RotateToRight(subR);
RotateToLeft(parent);
//subRL平衡因子决定最后的平衡因子
if (balanceFactor == -1)
{
subRL->_balanceFactor = 0;
parent->_balanceFactor = 0;
subR->_balanceFactor = 1;
}
else if (balanceFactor == 1)
{
subRL->_balanceFactor = 0;
parent->_balanceFactor = -1;
subR->_balanceFactor = 0;
}
else if (balanceFactor == 0)
{
subRL->_balanceFactor = 0;
parent->_balanceFactor = -1;
subR->_balanceFactor = 0;
}
}3.2.4 左右双旋
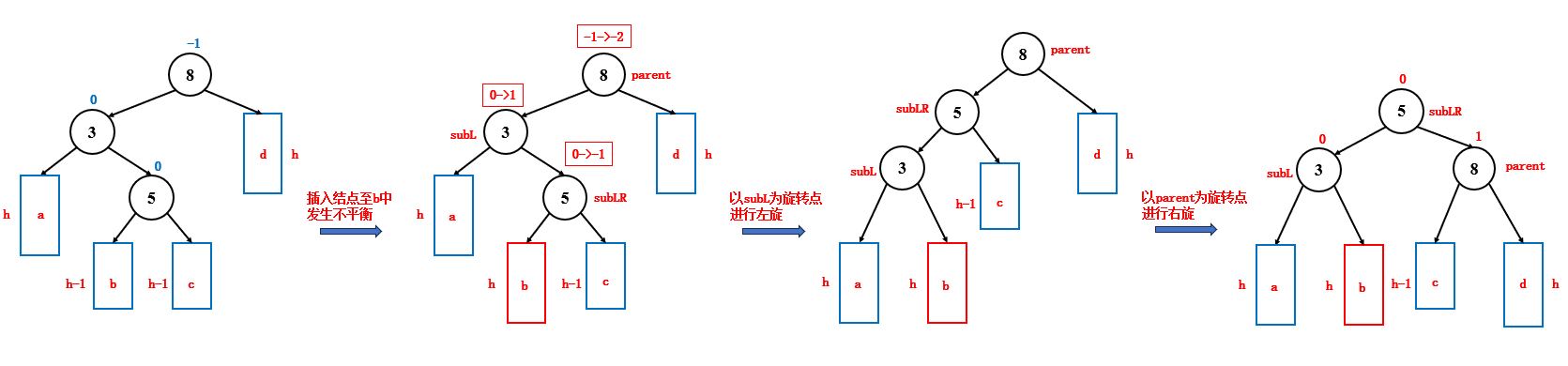
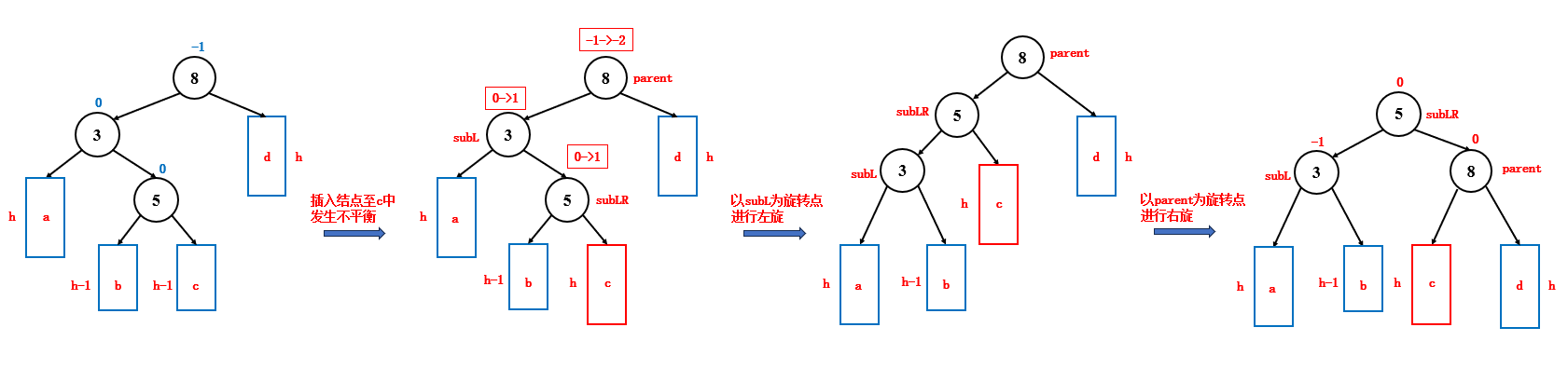
如果新插入的结点位于父结点左子树的右子树中,并且此时发生了不平衡,就要进行左右双旋来调整平衡,左右双旋时,结点和平衡因子的变化如下:
subLR 的平衡因子,说明了新结点插入到了 b 中还是 c 中,会直接影响到最后 parent,subLR,subL 的平衡因子,因为 b 和 c 这两棵子树旋转后的位置是不一样的
- subLR 平衡因子为 -1,那么最后 parent 平衡因子为 0,subLR 平衡因子为1,subL 平衡因子为 0
- subLR 平衡因子为 1,那么最后 parent 平衡因子为 -1,subLR 平衡因子为 0,subL 平衡因子为 0
- subLR 平衡因子为 0,那么最后 parent 平衡因子为 0,subLR 平衡因子为 0,subL 平衡因子为 0
左右双旋代码实现:
cpp
void RotateToLeftThenToRight(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int balanceFactor = subLR->_balanceFactor;
RotateToLeft(subL);
RotateToRight(parent);
if (balanceFactor == -1)
{
subLR->_balanceFactor = 0;
parent->_balanceFactor = 1;
subL->_balanceFactor = 0;
}
else if (balanceFactor == 1)
{
subLR->_balanceFactor = 0;
parent->_balanceFactor = 0;
subL->_balanceFactor = -1;
}
else if (balanceFactor == 0)
{
subLR->_balanceFactor = 0;
parent->_balanceFactor = 0;
subL->_balanceFactor = 0;
}
else
{
assert(false);
}
}4 二叉平衡树的查找
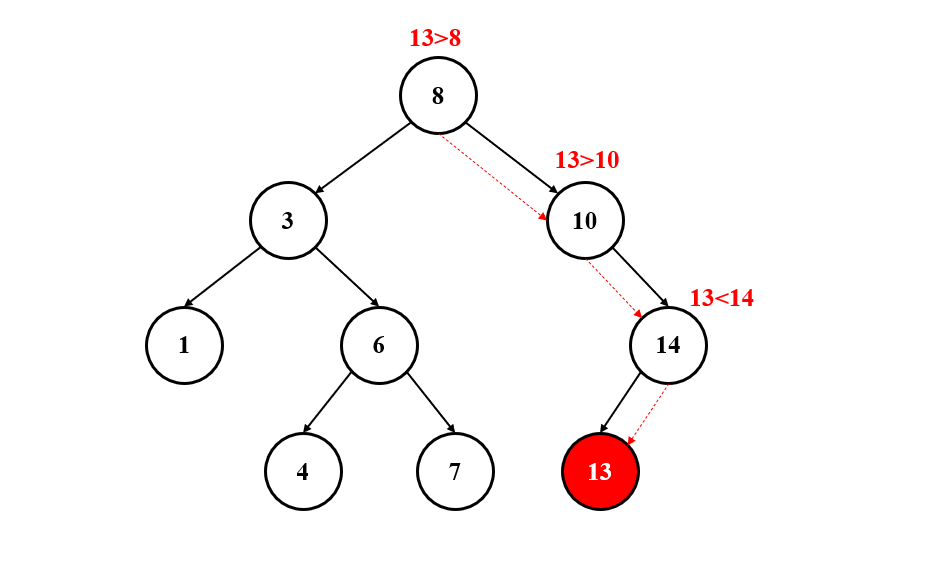
二叉平衡树的查找十分简单,与二叉排序树类似,只需要使用传入函数的值 key 与结点的值进行对比,在树中进行移动即可:
- key < 结点的值,向左子树移动
- key > 结点的值,向右子树移动
- key == 结点的值,查找到返回 true
- 未查找到返回 false
cpp
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key > cur->_kv.first)
{
cur = cur->_right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}5 二叉平衡树的代码
cpp
//AVL树的结点
template<class K, class V>
struct AVLTreeNode
{
pair<K, V> _kv; //存储的键值对
AVLTreeNode<K, V>* _left; //指向左孩子的指针
AVLTreeNode<K, V>* _right; //指向右孩子的指针
AVLTreeNode<K, V>* _parent; //指向父结点的指针
int _balanceFactor; //平衡因子
AVLTreeNode(const pair<K, V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_balanceFactor(0)
{}
};
//AVL树本体
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
//查找
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key > cur->_kv.first)
{
cur = cur->_right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
//插入
bool Insert(const pair<K, V>& kv)
{
if (!_root)
{
_root = new Node(kv);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kv.first > cur->_kv.first) //大于向右子树移动
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first) //小于向左子树移动
{
parent = cur;
cur = cur->_left;
}
else //等于则不进行插入,去重
{
return false;
}
}
cur = new Node(kv);
cur->_parent = parent;
if (cur->_kv.first < parent->_kv.first) //在父结点的左子树中插入
{
parent->_left = cur;
}
else if (cur->_kv.first > parent->_kv.first) //在父结点的右子树中插入
{
parent->_right = cur;
}
while (parent)
{
//更新父结点的平衡因子
if (cur == parent->_left)
{
parent->_balanceFactor--;
}
else if (cur == parent->_right)
{
parent->_balanceFactor++;
}
if (parent->_balanceFactor == 0)
{
break;
}
else if (parent->_balanceFactor == 1 || parent->_balanceFactor == -1) //平衡因子是1或-1
{
//继续向上更新
cur = parent;
parent = parent->_parent;
}
else if (parent->_balanceFactor == 2 || parent->_balanceFactor == -2) //平衡因子是2或-2
{
//旋转
if (cur->_balanceFactor == -1 && cur == parent->_left) //插入在左子树的左子树中不平衡
{
RotateToRight(parent);
}
else if (cur->_balanceFactor == 1 && cur == parent->_right) //插入在右子树的右子树中不平衡
{
RotateToLeft(parent);
}
else if (cur->_balanceFactor == -1 && cur == parent->_right) //右左双旋
{
RotateToRightThenToLeft(parent);
}
else if (cur->_balanceFactor == 1 && cur == parent->_left) //左右双旋
{
RotateToLeftThenToRight(parent);
}
else
{
assert(false);
}
}
else
{
assert(false);
}
}
return true;
}
//右单旋
void RotateToRight(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* grandParent = parent->_parent;
//更新子树
subL->_right = parent;
parent->_left = subLR;
parent->_parent = subL;
if (subLR)
subLR->_parent = parent;
if (parent == _root) //父结点是根节点,更新根节点
{
_root = subL;
subL->_parent = nullptr;
}
else //如果父结点不是根节点,那么要更新组父结点
{
subL->_parent = grandParent;
if (grandParent->_left == parent)
{
grandParent->_left = subL;
}
else if (grandParent->_right == parent)
{
grandParent->_right = subL;
}
}
subL->_balanceFactor = 0;
parent->_balanceFactor = 0;
}
//左单旋
void RotateToLeft(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* grandParent = parent->_parent;
//更新子树
subR->_left = parent;
parent->_right = subRL;
parent->_parent = subR;
if (subRL)
subRL->_parent = parent;
if (parent == _root) //父结点是根节点,更新根节点
{
_root = subR;
subR->_parent = nullptr;
}
else //如果父结点不是根节点,那么要更新组父结点
{
subR->_parent = grandParent;
if (grandParent->_left == parent)
{
grandParent->_left = subR;
}
else if (grandParent->_right == parent)
{
grandParent->_right = subR;
}
}
//旋转后一定平衡,更新平衡因子
subR->_balanceFactor = 0;
parent->_balanceFactor = 0;
}
//右左双旋
void RotateToRightThenToLeft(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int balanceFactor = subRL->_balanceFactor;
RotateToRight(subR);
RotateToLeft(parent);
//subRL平衡因子决定最后的平衡因子
if (balanceFactor == -1)
{
subRL->_balanceFactor = 0;
parent->_balanceFactor = 0;
subR->_balanceFactor = 1;
}
else if (balanceFactor == 1)
{
subRL->_balanceFactor = 0;
parent->_balanceFactor = -1;
subR->_balanceFactor = 0;
}
else if (balanceFactor == 0)
{
subRL->_balanceFactor = 0;
parent->_balanceFactor = -1;
subR->_balanceFactor = 0;
}
else
{
assert(false);
}
}
//左右双旋
void RotateToLeftThenToRight(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int balanceFactor = subLR->_balanceFactor;
RotateToLeft(subL);
RotateToRight(parent);
if (balanceFactor == -1)
{
subLR->_balanceFactor = 0;
parent->_balanceFactor = 1;
subL->_balanceFactor = 0;
}
else if (balanceFactor == 1)
{
subLR->_balanceFactor = 0;
parent->_balanceFactor = 0;
subL->_balanceFactor = -1;
}
else if (balanceFactor == 0)
{
subLR->_balanceFactor = 0;
parent->_balanceFactor = 0;
subL->_balanceFactor = 0;
}
else
{
assert(false);
}
}
private:
Node* _root = nullptr;
};