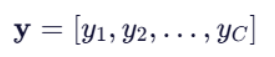本文系统性地梳理PyTorch交叉熵损失的完整知识体系:从Softmax的数学原理,到信息论基础,再到CrossEntropyLoss的每个细节及API介绍,最后通过代码验证。构建清晰的理解框架,彻底解决相关困惑。
目录:
[4、nn.CrossEntropyLoss 的 y_true 是什么样](#4、nn.CrossEntropyLoss 的 y_true 是什么样)
[5、nn.CrossEntropyLoss - API介绍](#5、nn.CrossEntropyLoss - API介绍)
[6、CrossEntropyLoss需要 long(torch.int64)](#6、CrossEntropyLoss需要 long(torch.int64))
1、Softmax 激活函数
Softmax就是将网络输出的logits通过Softmax函数,映射成为(0,1)的值,而这些值的累和为1(满足概率的性质),那么我们将它理解成概率,选取概率最大(也就是值对应最大的)节点,作为我们的预测目标类别。
非常好的问题!我们来一步步解释:全连接神经网络(Fully Connected Neural Network)最后一层的输出是什么?是不是一定为 1?和 logits 有什么关系?
✅ 简短回答:
-
最后一层的输出不一定是 1。
-
最后一层的原始输出就是 logits(未归一化的分数)。
-
logits 的维度 = 类别数(比如 4 分类 → 输出是 4 个实数)。
-
只有经过 Softmax 后,输出才是概率分布(总和为 1)。
🧠 详细解释
1. 什么是 logits?
Logits 是模型最后一层(通常是线性层,即 nn.Linear)直接输出的未归一化分数 。它们可以是任意实数(正、负、很大或很小),不需要加起来等于 1。
例如,对于一个 4 分类任务:
python
# 假设最后一层是 nn.Linear(in_features=..., out_features=4)
logits = model(x) # shape: [batch_size, 4]
# 某个样本的 logits 可能是: [-0.5, 2.3, 1.0, -1.2]这些值本身没有概率意义 ,但它们的相对大小决定了哪个类别更可能。
2. 全连接网络的最后一层结构
假设网络结构如下(以单个样本为例):
-
输入:3 个特征 →
[x1, x2, x3] -
隐藏层:若干全连接层(比如 64 → 32 神经元)
-
输出层 :
nn.Linear(32, 4)→ 输出 4 个值(对应 4 个类别)
这个输出层没有激活函数 (或者说是恒等激活),所以它的输出就是 logits。
🔸 关键点:分类任务中,最后一层通常不加激活函数(如 ReLU、Sigmoid) ,因为后续的损失函数(如
CrossEntropyLoss)或 Softmax 会处理它。
3. 什么时候输出"和为 1"?
只有当你对 logits 应用 Softmax之后,才会得到概率分布,此时:
-
每个值 ∈ (0, 1)
-
所有值之和 = 1
python
import torch
logits = torch.tensor([-0.5, 2.3, 1.0, -1.2])
probs = torch.softmax(logits, dim=-1)
print(probs) # e.g., [0.03, 0.62, 0.17, 0.01]
print(probs.sum()) # tensor(1.)4. 训练时通常不用显式计算 Softmax !
PyTorch 的 nn.CrossEntropyLoss 内部已经做了两件事:
-
对输入(logits)自动应用 log-softmax
-
再计算 负对数似然损失(NLLLoss)
所以你训练时直接传 logits 给损失函数即可:
python
criterion = nn.CrossEntropyLoss()
loss = criterion(logits.unsqueeze(0), target) # logits shape: [1, 4], target: [0]✅ 这样做更高效、数值更稳定,也避免了重复计算 Softmax 。
📌 总结对比
| 阶段 | 输出名称 | 是否归一化 | 和是否为 1 | 用途 |
|---|---|---|---|---|
| 最后一层线性输出 | logits | ❌ 否 | ❌ 不一定 | 传给损失函数或 Softmax |
| 经过 Softmax 后 | probabilities | ✅ 是 | ✅ 是 | 用于预测概率、可视化 |
💡 举个完整例子(4 分类,输入 3 特征)
python
import torch
import torch.nn as nn
# 定义简单网络
model = nn.Sequential(
nn.Linear(3, 10), # 输入3特征 → 10隐藏单元
nn.ReLU(),
nn.Linear(10, 4) # 输出4个logits(4分类)
)
x = torch.randn(1, 3) # 一个样本,3个特征
logits = model(x) # shape: [1, 4]
print("logits:", logits) # 如: [[-0.2, 1.5, 0.8, -0.9]]
print("sum of logits:", logits.sum()) # 不等于1!
probs = torch.softmax(logits, dim=-1)
print("probabilities:", probs) # 如: [[0.12, 0.58, 0.28, 0.02]]
print("sum of probs:", probs.sum()) # = 1.0torch.softmax 是怎么计算的?
🎯 背景设定
-
你有一个 4 分类问题(即类别数 K = 4)。
-
某个样本经过模型(比如一个全连接层)后,输出了一个 长度为 4 的 logits 向量,例如:
logits = [2.0, 1.0, 1.5, 3.0] # 这是模型原始输出,未归一化💡 注意:你说"有 3 个特征",这通常是指输入特征维度 。但
Softmax是作用在模型输出(logits) 上的,而 logits 的维度等于类别数(这里是 4)。所以不管输入有几个特征,只要输出是 4 维,Softmax就会在这 4 个值上操作。
🔢 Softmax 公式
对 logits 向量 ,
Softmax计算每个类别的概率为:
其中 K = 4(4 分类)。
🧮 举个例子
假设 logits 是:
python
import torch
logits = torch.tensor([2.0, 1.0, 1.5, 3.0])应用 Softmax(通常在最后一个维度,dim=-1):
python
probs = torch.softmax(logits, dim=-1) # 原始得分(logits)越高,经过 Softmax 函数转换后对应的概率就越大
print(probs)计算过程如下:
1. 计算指数:
2. 求和:
3. 归一化:
所以输出概率大约是:
python
[0.213, 0.078, 0.129, 0.580]这些值加起来为 1,符合概率分布。
✅ 回到你的例子
你说预测结果是 [0.1, 0.1, 0.2, 0.6],这是完全可能的!只要对应的 logits 经过 Softmax 后得到这个分布即可。例如,logits 可能是类似 [0, 0, 1, 2] 这样的值(具体数值可通过反推得到)。
⚠️ 注意事项
-
Softmax作用于 logits(未归一化的分数),不是原始输入特征。 -
输入特征维度(如你提到的 3 个特征)会影响模型如何生成 logits,但
Softmax本身只关心 logits 的维度(必须等于类别数)。 -
在 PyTorch 中,通常在分类模型最后用
torch.softmax(..., dim=-1),或直接用CrossEntropyLoss(它内部自动做Softmax + log + NLL)。
💡 小技巧:数值稳定性
实际实现中,PyTorch 会对 logits 减去最大值以避免指数溢出:
python
# 等价于 torch.softmax(z, dim=-1)
z = logits - logits.max(dim=-1, keepdim=True).values
probs = torch.exp(z) / torch.exp(z).sum(dim=-1, keepdim=True)示例代码:
python
import torch
# 共 10 个类,每个类别得分分别为
y = torch.tensor(data=[[0.2, 0.02, 0.15, 0.15, 1.3, 0.5, 0.06, 1.1, 0.05, 3.75],
[0.2, 0.02, 0.15, 3.75, 1.3, 0.5, 0.06, 1.1, 0.05, 0.15]])
# Softmax 激活函数转换成概率值, 根据得分把类别得分转为对应 概率, 总概率和为 1
# dim: 指定在哪一个维度上进行归一化(即对哪个维度做求和为 1 的操作)
y_softmax = torch.softmax(input=y, dim=1) # dim=1:对每一行(即每个样本的 10 个 logits)做 Softmax → 每一行的概率和为 1。
print(y_softmax)
# tensor([[0.0212, 0.0177, 0.0202, 0.0202, 0.0638, 0.0287, 0.0185, 0.0522, 0.0183, 0.7392],
# [0.0212, 0.0177, 0.0202, 0.7392, 0.0638, 0.0287, 0.0185, 0.0522, 0.0183, 0.0202]])
y_softmax2 = torch.softmax(input=y, dim=0) # dim=0:对每一列做 Softmax → 每一列的两个值加起来为 1(这在分类任务中通常没有意义)。
print(y_softmax2)
# tensor([[0.5000, 0.5000, 0.5000, 0.0266, 0.5000, 0.5000, 0.5000, 0.5000, 0.5000, 0.9734],
# [0.5000, 0.5000, 0.5000, 0.9734, 0.5000, 0.5000, 0.5000, 0.5000, 0.5000, 0.0266]])解释:
Softmax 是一种常用于多分类任务的激活函数,它将一组实数(通常称为"logits")转换为概率分布------即每个元素变为非负数,且所有元素之和为 1。
Softmax 的计算公式
对于一个向量 ,其 Softmax 输出为:
为了数值稳定性,实际计算中通常会减去最大值(PyTorch 内部已自动处理):
这样可以避免指数爆炸(如 虽不大,但若输入是 1000 就会溢出)。
dim 参数的作用
在 PyTorch 中,torch.softmax(input, dim=...) 的 dim 参数指定在哪一个维度上进行归一化(即对哪个维度做求和为 1 的操作)。
-
对于 二维张量 (如你的例子:形状为
[2, 10],表示 2 个样本,每个有 10 个类别):-
dim=1:对每一行(即每个样本的 10 个 logits)做 Softmax → 每一行的概率和为 1。 -
dim=0:对每一列做 Softmax → 每一列的两个值加起来为 1(这在分类任务中通常没有意义)。
-
✅ 在分类任务中,几乎总是用 dim=1(对类别维度归一化)。
代码示例解析
python
y = torch.tensor([[0.2, 0.02, ..., 3.75],
[0.2, 0.02, ..., 0.15]]) # shape: (2, 10)
y_softmax = torch.softmax(y, dim=1)-
对第 0 行:将
[0.2, 0.02, ..., 3.75]转换为一个 10 维概率分布,其中 3.75 对应的位置概率最大。 -
对第 1 行:
3.75出现在第 3 位(索引 3),所以该位置的概率最高。 -
每一行的 10 个数加起来都等于 1。
你可以验证:
python
print(y_softmax.sum(dim=1)) # 输出: tensor([1., 1.])用最直观的方式 解释 dim=0 和 dim=1 在 torch.softmax 中的区别,结合例子(2 行 10 列的张量)一步步说明。
🧱 先看数据形状
python
y = torch.tensor([[0.2, 0.02, 0.15, 0.15, 1.3, 0.5, 0.06, 1.1, 0.05, 3.75], # ← 第0个样本
[0.2, 0.02, 0.15, 3.75, 1.3, 0.5, 0.06, 1.1, 0.05, 0.15]]) # ← 第1个样本-
形状是
(2, 10):2 个样本,每个有 10 个类别得分(logits) -
我们希望:每个样本自己的 10 个得分 → 转成一个概率分布(和为 1)
这正是 dim=1 的作用!
✅ 情况一:dim=1(最常用)
"对每一行内部做 Softmax"
-
操作维度:第 1 维(列方向)
-
对 第 0 行 的 10 个数做 Softmax → 得到 10 个概率,加起来 = 1
-
对 第 1 行 的 10 个数做 Softmax → 得到另 10 个概率,加起来 = 1
🧠 理解口诀:
dim=1→ "按行归一化",每行自己变成概率分布。
✅ 这就是分类任务的标准做法!
❓情况二:dim=0(很少用在分类中)
"对每一列内部做 Softmax"
-
操作维度:第 0 维(行方向)
-
看 第 0 列 :有两个数
[0.2, 0.2]→ Softmax 后变成两个概率,加起来 = 1 -
看 第 1 列 :
[0.02, 0.02]→ Softmax 后也是两个数,和 = 1 -
......一直到第 9 列
🧠 理解口诀:
dim=0→ "按列归一化",每列自己变成概率分布。
⚠️ 但在分类任务中,两个不同样本的同一类别之间没有"竞争关系",所以这样没意义!
🔍 举个具体数字例子
假设简化版 y 只有 2 行 3 列:
python
y = [[1, 2, 3],
[4, 5, 6]]➤ softmax(y, dim=1):
-
第0行:softmax([1,2,3]) → [~0.09, ~0.24, ~0.67](和=1)
-
第1行:softmax([4,5,6]) → [~0.09, ~0.24, ~0.67](和=1)
-
结果形状仍是 (2,3)
➤ softmax(y, dim=0):
-
第0列:softmax([1,4]) → [e¹/(e¹+e⁴), e⁴/(e¹+e⁴)] ≈ [0.05, 0.95]
-
第1列:softmax([2,5]) → ≈ [0.05, 0.95]
-
第2列:softmax([3,6]) → ≈ [0.05, 0.95]
-
结果也是 (2,3),但每列和为1,不是每行!
📌 总结一句话
dim= |
含义 | 应用场景 |
|---|---|---|
1 |
对每个样本的类别得分做归一化 → 每行和为1 | ✅ 多分类任务(标准用法) |
0 |
对每个类别在所有样本上的得分做归一化 → 每列和为1 | ❌ 分类中几乎不用 |
💡 记住:你有多少个样本,就有多少个独立的概率分布 。所以要在"样本内部"归一化 → 用
dim=1(当数据是[batch_size, num_classes]时)。
✅ 验证小技巧
运行这行代码就能看清:
python
print("dim=1 时每行和:", torch.softmax(y, dim=1).sum(dim=1)) # → [1., 1.]
print("dim=0 时每列和:", torch.softmax(y, dim=0).sum(dim=0)) # → [1., 1., ..., 1.] (共10个1)总结
| 项目 | 说明 |
|---|---|
| Softmax 作用 | 将 logits 转为概率分布 |
| 公式核心 | |
dim 含义 |
在哪个维度上做归一化(使该维度上的元素和为 1) |
| 分类任务常用 | dim=1(对每个样本的类别维度归一化) |
💡 提示:在 PyTorch 中,如果你使用
CrossEntropyLoss,不需要手动加 Softmax,因为它内部已经结合了 LogSoftmax 和 NLLLoss,直接输入原始 logits 即可。
2、信息量、熵、交叉熵
🎯 核心概念:衡量"惊讶程度"
想象你是一个天气预报员,交叉熵就是在衡量你的预测让观众有多"惊讶"。
📚 基础理解
- 信息量
-
如果我说"太阳从东边升起",你不会惊讶 → 信息量小
-
如果我说"今天下雪了"(在夏天),你会很惊讶 → 信息量大
数学表达:信息量 = -log(概率)
- 熵(Entropy)
-
衡量事件本身的不确定性
-
比如抛硬币:正反面各50%,不确定性很高
-
比如太阳升起:100%从东边,不确定性为0
- 交叉熵(Cross Entropy)
用你的预测分布,去衡量真实事件发生时的平均惊讶程度
🍎 具体例子
例1:水果分类
真实情况:这是一个苹果
| 预测 | 概率 | 惊讶程度计算 |
|---|---|---|
| 认为是苹果 | 90% | -log(0.9) ≈ 0.1 (不太惊讶) |
| 认为是橙子 | 8% | -log(0.08) ≈ 2.5 (很惊讶) |
| 认为是香蕉 | 2% | -log(0.02) ≈ 3.9 (非常惊讶) |
交叉熵 ≈ 0.1(因为真实是苹果,我们只关心这个)
例2:考试成绩预测
真实情况:学生考了A等
你的预测:
-
A: 30% → -log(0.3) ≈ 1.20
-
B: 50% → -log(0.5) ≈ 0.69
-
C: 20% → -log(0.2) ≈ 1.61
交叉熵 = 1.20(因为真实是A,只用A的惊讶程度)
🔄 在机器学习中的应用
多分类问题
真实标签:猫
模型预测:狗:30%, 猫:60%, 鸟:10%
交叉熵 = -log(0.6) ≈ 0.51
真实标签:猫
模型预测:狗:10%, 猫:85%, 鸟:5%
交叉熵 = -log(0.85) ≈ 0.16第二个预测更好,交叉熵更小!
💡 关键特性
-
非负性:交叉熵 ≥ 0
-
不对称性:用预测分布衡量真实分布 ≠ 反过来
-
完美预测:当预测概率=100%时,交叉熵=0
-
惩罚自信的错误:如果错误但很自信,惩罚很大
🎯 核心思想总结
交叉熵回答的问题是: "如果我按照我的预测分布来相信世界,当真实事件发生时,我平均会有多惊讶?"
在机器学习中:
-
目标:让交叉熵最小化
-
意义:让模型的预测分布尽可能接近真实分布
-
效果:模型会对正确的类别给出高概率,对错误类别给出低概率
3、CrossEntropyLoss
一、目标:让模型"猜得准"
假设你训练一个模型来做图像分类,比如判断一张图是「猫」「狗」还是「鸟」。 模型看到图片后,会输出一个"猜测"------比如:
-
猫:30%
-
狗:60%
-
鸟:10%
而真实答案是「狗」。
我们希望:当真实答案是某个类别时,模型给这个类别的概率越高越好 。 如果猜错了(比如把「狗」说成「猫」概率最高),就要"惩罚"它------这个"惩罚"的大小,就是损失(loss)。
二、怎么量化"惩罚"?------引入交叉熵
交叉熵(Cross-Entropy)是一种衡量两个概率分布差异的方法。
在分类问题中:
-
真实分布:只有一个类别是 100%,其他都是 0。 比如真实是「狗」→ 真实分布 = [0, 1, 0]
-
预测分布:模型输出的概率,比如 [0.3, 0.6, 0.1]
交叉熵公式(对单个样本,不是对所有样本):
也可以写成:
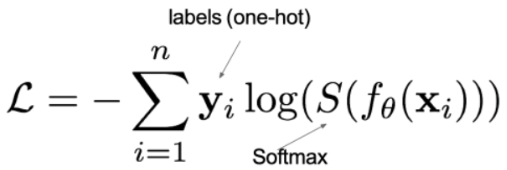
其中:
是真实分布的第 i 个值(只有正确类别是 1,其余是 0),就是 one-hot 编码
对于 C 个类别,真实分布是一个长度为 C 的向量:
是模型预测的第 i 个类别的概率,即模型认为该样本属于第 i 个类别的概率 ,就是经过 Softmax 函数得到的概率,比如 Softmax 后 ≈
[0.76, 0.05, 0.19]
因为真实分布中只有一个 1,其余都是 0
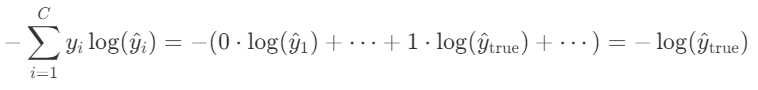
所以求和后其实只剩一项,在标准多分类任务中,交叉熵损失的真正公式是这个:
👉 也就是说:只看模型给"正确答案"分配的概率是多少,然后取负对数!
例子:
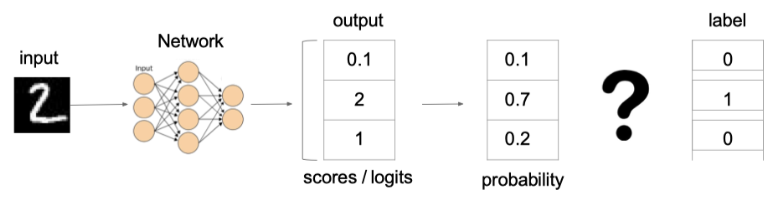
上图中的交叉熵损失为:
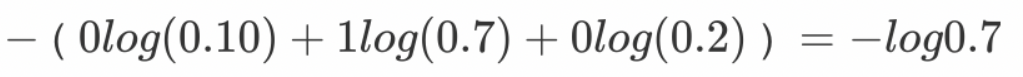
从概率角度理解,我们的目的是最小化正确类别所对应的预测概率的对数的负值(损失值最小),如下图所示:
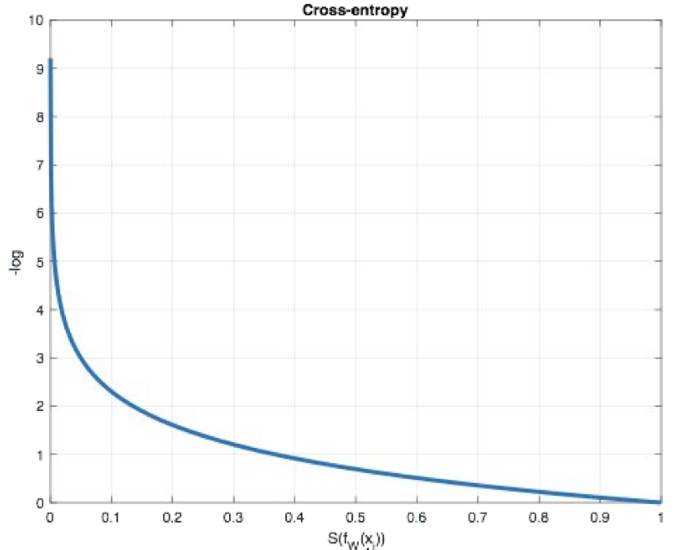
三、为什么用 -log(p)?
我们来看看这个函数的性质:
| 模型给正确类别的概率 p | 损失 |
|---|---|
| 1.0(完全猜对) | 0 |
| 0.9 | ≈0.11 |
| 0.5 | ≈0.69 |
| 0.1 | ≈2.30 |
| 0.01 | ≈4.61 |
✅ 特点:
-
概率越高 → 损失越小(理想情况损失为 0)
-
概率越低 → 损失急剧增大(严厉惩罚错误)
而且,对数函数在优化时梯度性质好,适合梯度下降。
四、实际中,模型不直接输出概率!
你可能会问:模型输出的是 logits(比如 [2.1, -0.5, 1.0]),不是概率啊?
没错!但 CrossEntropyLoss 把两步合并了:
- 先对 logits 做 Softmax→ 变成概率分布
(Softmax 能保证所有输出加起来为 1,且都是正数)
- 再计算交叉熵
所以,你喂给 CrossEntropyLoss 的是原始分数(logits),它内部自动处理成概率再算 loss。
💡 这样做不仅方便,还能避免数值不稳定(比如直接对 Softmax 后的小概率取 log 容易溢出)。
五、举个生活化的例子 🌰
想象你在考试,老师问:"这张图是猫、狗还是鸟?"
-
如果你非常确定是狗,写"狗:99%",结果真是狗 → 老师给你高分(loss 很小)
-
如果你瞎猜"狗:33%",结果真是狗 → 老师觉得你不太行(loss 中等)
-
如果你坚定地说"猫:90%",结果是狗 → 老师很生气(loss 很大!)
CrossEntropyLoss 就是这位"打分老师",根据你对正确答案的信心程度来打分。
六、总结一句话
CrossEntropyLoss 衡量的是:模型对正确类别的"自信程度"。越自信且正确,损失越小;越不自信或错误,损失越大。
它是分类任务的"黄金标准"损失函数,几乎所有的图像分类、文本分类等都用它。
4、nn.CrossEntropyLoss 的 y_true 是什么样
✅ 真实标签(y_true)只有「一种正确形式」用于 CrossEntropyLoss
在 PyTorch 的 nn.CrossEntropyLoss 中,y_true 必须是「类别索引」(整数),而不是概率、得分或 one-hot 向量。
正确的 y_true 形式(对 CrossEntropyLoss):
-
类型:整数(long)
-
形状:
(N,),其中 N 是样本数量 -
值:每个元素是 0 到 C−1 之间的整数,表示该样本属于哪一类
✅ 例子(3 分类,2 个样本):
y_true = [1, 0] # 第一个样本是第1类,第二个是第0类🔸 这对应于你所说的"分类结果",但它不是数组
[1, 0, 0],而是单个整数0表示"第0类"。
❌ 下面这些形式 不能直接用于 CrossEntropyLoss:
1. One-hot 编码 (如 [1, 0, 0])
这是你提到的"真实分布 = [1, 0, 0]"的形式。 虽然从数学上讲,交叉熵确实是在比较两个概率分布(真实分布 vs 预测分布),但 PyTorch 的 CrossEntropyLoss 并不要求你传入这个 one-hot 向量。
为什么?
-
因为 one-hot 向量中只有一个 1,其余都是 0,信息完全等价于"类别索引"。
-
用整数索引更节省内存、计算更快。
👉 所以:[1, 0, 0] → 应该写成 0;[0, 1, 0] → 写成 1
2. 得分/ logits(如 [1.2, 4.5, 6.7])
这是模型输出的形式(y_pred) ,绝不能用作 y_true!
-
y_true是真实标签,必须是确定的类别(人类标注的结果),不可能是连续得分。 -
如果你有"软标签"(比如 [0.2, 0.3, 0.5] 表示不确定),那属于标签平滑(label smoothing) 或 知识蒸馏 场景,这时也不能用标准
CrossEntropyLoss,而要用其他方式(比如手动计算 KL 散度或使用F.kl_div)。
📌 总结对比表
| 标签形式 | 示例(3分类) | 能否用于 nn.CrossEntropyLoss 的 y_true? |
说明 |
|---|---|---|---|
| 类别索引(整数) | [1, 0] |
✅ 可以(标准用法) | 每个样本一个整数 |
| One-hot 向量 | [[0,1,0], [1,0,0]] |
❌ 不可以 | 需转换为索引:[1, 0] |
| 连续得分 / logits | [[1.2,4.5,6.7], ...] |
❌ 绝对不可以 | 这是 y_pred 的格式 |
| 软概率(非 one-hot) | [[0.2,0.3,0.5], ...] |
❌ 标准 CrossEntropyLoss 不支持 | 需自定义损失函数 |
💡 补充:什么时候会用到 one-hot 形式的"真实分布"?
只有在以下情况才需要:
-
你自己实现交叉熵损失
-
使用
BCEWithLogitsLoss(用于多标签分类) -
做 label smoothing(标签平滑):把
[1,0,0]变成[0.9, 0.05, 0.05] -
知识蒸馏:用 teacher 模型输出的概率作为 soft label
CrossEntropyLoss :
y_true= 类别索引(整数)BCEWithLogitsLoss (二分类):
y_true= one-hot样式MSELoss (回归):
y_true= 连续值
但在标准的多分类任务中 ,y_true 就是一个整数类别标签,简洁高效。
| 形式 | 例子 | 适用损失函数 | 特点 |
|---|---|---|---|
| 类别标签 | [1, 2, 0] |
CrossEntropyLoss | 简洁,内存小 |
| One-hot | [[0,1,0],[0,0,1],[1,0,0]] |
BCELoss等 | 直观,但冗余 |
✅ 记住一句话:
给
nn.CrossEntropyLoss的y_true,永远是"第几类"的整数编号,不是向量,不是分数,不是概率。
5、nn.CrossEntropyLoss - API介绍
🔧 一、基本定义
python
torch.nn.CrossEntropyLoss(
weight=None, # 给不同类别分配不同权重,常用于类别不平衡场景
size_average=None,
ignore_index=-100, # 忽略某些标签
reduce=None,
reduction='mean' # 控制如何聚合每个样本的 loss
)⚠️ 注意:
size_average和reduce已废弃,统一用reduction控制。
📥 二、输入要求(最重要!)
| 参数 | 形状 | 类型 | 说明 |
|---|---|---|---|
input(即 y_pred) |
(N, C) 或 (N, C, d1, d2, ...) |
float |
模型原始 logits(未经过 Softmax) • N: batch size • C: 类别数 |
target(即 y_true) |
(N,) 或 (N, d1, d2, ...) |
long(整数) |
真实类别索引(0 到 C−1) |
✅ 关键点:
-
input不需要做 Softmax!CrossEntropyLoss 内部会自动处理。 -
target必须是 整数类型(如torch.long),不能是 float 或 one-hot。
⚙️ 三、主要参数详解
1. reduction(最常用)
控制如何聚合每个样本的 loss:
-
'none':返回每个样本的 loss,形状同target -
'mean':返回所有样本 loss 的平均值(默认) -
'sum':返回所有样本 loss 的总和
第一种:reduction='none'
✅ 公式:

💡 输出:
-
形状:
(N,) -
每个元素是单个样本的损失
-
不聚合,保留所有信息
📌 用途:
-
分析每个样本的 loss 大小
-
自定义加权、mask、或做异常检测
第二种:reduction='sum'
✅ 公式:
💡 输出:
-
标量(scalar)
-
所有样本 loss 的总和
📌 用途:
-
需要精确控制梯度总量(如某些理论推导)
-
与 batch size 相关,不适合直接比较不同 batch 的 loss
第三种:reduction='mean'(默认)
✅ 公式:
💡 输出:
-
标量
-
平均每个样本的损失
📌 用途:
-
最常用! 因为 loss 值不随 batch size 变化,便于调试和监控
-
训练时稳定、可比性强
📊 表格
| reduction | 公式 | 输出形状 | 是否推荐 |
|---|---|---|---|
'none' |
(N,) |
特殊需求用 | |
'sum' |
()(标量) |
少用 | |
'mean' |
()(标量) |
✅ 强烈推荐 |
python
# 示例
criterion = nn.CrossEntropyLoss(reduction='mean') # 默认
criterion = nn.CrossEntropyLoss(reduction='sum')
criterion = nn.CrossEntropyLoss(reduction='none') # 返回 [loss1, loss2, ...]2. weight(处理类别不平衡)
-
类型:1D 张量,长度 = 类别数 C
-
用途:给不同类别分配不同权重,常用于类别不平衡场景
每个样本损失乘以其类别权重
则:
- 再按
reduction聚合(但分母仍是样本数,不是权重和)
python
# 比如3分类,第2类样本少,给更高权重
weight = torch.tensor([1.0, 1.0, 5.0]) # 当样本真实标签是类别 2 时,其 loss 会被乘以 5。
criterion = nn.CrossEntropyLoss(weight=weight)3. ignore_index
-
类型:整数(默认
-100) -
用途:忽略某些标签 (常用于 NLP 中的 padding)。在所有
target里,凡是值等于ignore_index的位置,一律不计入损失 ,既不参与求和,也不参与求平均,反向传播时这些位置梯度直接为0。
忽略某些样本(比如 padding)
设有效样本数为
'mean'实际是:
python
# 比如标签中 -1 表示无效位置,不想让它参与 loss 计算
# criterion = nn.CrossEntropyLoss(ignore_index=2) # 忽略真实标签为 类别2 对应的样本
# 忽略真实标签为2的样本
criterion = nn.CrossEntropyLoss(ignore_index=2)
# 忽略填充标签-100
criterion = nn.CrossEntropyLoss(ignore_index=-100)
# 忽略背景类别0
criterion = nn.CrossEntropyLoss(ignore_index=0)
criterion = nn.CrossEntropyLoss(ignore_index=-1)
y_true = torch.tensor([1, 2, -1]) # 第3个样本被忽略✅ 被忽略的样本不会计入
mean或sum(即分母或总数会跳过它)
🧪 四、完整使用示例
场景:3 分类,batch_size=2
python
import torch
import torch.nn as nn
# 模型输出(logits),不需要 Softmax!
y_pred = torch.tensor([[2.0, 1.0, 0.1], # 样本1
[0.5, 1.5, 0.2]], # 样本2
dtype=torch.float32)
# 真实标签:样本1 属于第0类,样本2 属于第1类
y_true = torch.tensor([0, 1], dtype=torch.long) # 必须是 long!
# 创建损失函数
criterion = nn.CrossEntropyLoss(reduction='mean')
# 计算 loss
loss = criterion(y_pred, y_true)
print("Loss:", loss.item())输出(大致):
python
Loss: 0.894🔍 内部计算过程:
对每个样本做 Softmax → 得到概率
取真实类别对应的概率 → 取负对数
按
reduction方式聚合
🚫 五、常见错误 & 注意事项
| 错误 | 原因 | 解决方法 |
|---|---|---|
RuntimeError: expected scalar type Long but found Float |
y_true 是 float 类型 |
改为 torch.long |
IndexError: Target ... out of bounds |
y_true 中有 ≥C 或 <0 的值 |
检查标签范围是否在 [0, C-1] |
| loss 值非常大(如 >10) | 模型初期预测很差,或标签错位 | 检查 y_true 是否与类别对齐 |
| 用了 Softmax 再传入 | 多此一举,且可能导致数值不稳定 | 不要提前做 Softmax! |
📌 六、与其他损失函数对比
| 损失函数 | 适用任务 | y_true 格式 |
y_pred 格式 |
|---|---|---|---|
CrossEntropyLoss |
多分类(单标签) | 整数索引 | logits(未归一化) |
BCEWithLogitsLoss |
多标签分类 / 二分类 | 0/1 float(或 one-hot) | logits |
NLLLoss |
多分类 | 整数索引 | 已取 log 的概率(log_softmax 输出) |
💡
CrossEntropyLoss(input, target)等价于:
F.nll_loss(F.log_softmax(input, dim=1), target)
✅ 总结:正确使用步骤
-
模型输出 logits(不要加 Softmax)
-
真实标签用整数 (0, 1, 2, ..., C-1),类型为
torch.long -
创建
nn.CrossEntropyLoss(),按需设置reduction、weight、ignore_index -
调用
loss = criterion(y_pred, y_true) -
反向传播:
loss.backward()
如果你正在写训练循环,典型代码如下:
python
model = MyModel()
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters())
for x, y in dataloader: # y 是整数标签,shape=(N,)
pred = model(x) # pred shape=(N, C)
loss = criterion(pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()6、CrossEntropyLoss需要 long(torch.int64)
CrossEntropyLoss 标签类型要求
-
必须使用
torch.long(即torch.int64)nn.CrossEntropyLoss要求目标标签(target)是 64位整数类型,用于表示类别索引(如 0, 1, 2, ...)。 -
常见错误类型:
-
❌
torch.float32:浮点数,不能作为类别索引 -
❌
torch.int8/torch.int32:位宽不足,PyTorch 不接受
-
-
正确写法:
pythony = torch.tensor(labels, dtype=torch.long) # y = torch.tensor(labels, dtype=torch.int64) criterion = nn.CrossEntropyLoss() loss = criterion(y_predict, y_true) # y_true 必须是 long, 即 torch.int64 -
原因 : PyTorch 内部实现依赖
long类型进行索引操作,这是框架的硬性约定。
💡 记住口诀:分类标签用 long,其他类型会报错。
7、示例代码:
python
import torch
import torch.nn as nn
y_true = torch.tensor(data=[1, 2, 0]) # 3分类,`y_true` 必须是「类别索引」(整数)
print(y_true.dtype) # torch.int64
# 假设已经得到 logits 得分, 注意, 这不是Softmax得到的概率!
y_predict = torch.tensor(data=
[[1.2, 2.3, 5.6], # 样本0:类别2得分最高
[2.2, 5.6, 1.1], # 样本1:类别1得分最高
[1.1, 0.9, 6.66]]) # 样本2:类别2得分最高
print(f'使用 Softmax 得到的概率: \n{torch.softmax(y_predict, dim=1)}')
# tensor([[0.0117, 0.0352, 0.9531],
# [0.0320, 0.9574, 0.0106],
# [0.0038, 0.0031, 0.9930]])
# 【 Entropy n.熵 】
criterion = nn.CrossEntropyLoss()
loss = criterion(y_predict, y_true)
print(loss) # tensor(4.4862)