力扣hot100刷题记录（12.2）

35、LRU缓存

思路：双向链表+哈希表，双向链表存放put的元素，哈希表映射key的节点。

cpp 复制代码

class LRUCache {
public:
    int capacity;
    list<pair<int, int>> cache_list;
    unordered_map<int, list<pair<int, int>>::iterator> key_to_iter;

    LRUCache(int capacity) : capacity(capacity) {
        
    }
    
    int get(int key) {
        auto umap_iter = key_to_iter.find(key);
        if(umap_iter == key_to_iter.end()) return -1;

        auto list_iter = umap_iter->second;
        int value = list_iter->second;
        cache_list.erase(list_iter);
        cache_list.emplace_front(key, value);
        key_to_iter[key] = cache_list.begin();

        return value;
    }
    
    void put(int key, int value) {
        auto umap_iter = key_to_iter.find(key);
        if(umap_iter != key_to_iter.end()) {
            auto list_iter = umap_iter->second;

            cache_list.erase(list_iter);
            cache_list.emplace_front(key, value);
            key_to_iter[key] = cache_list.begin();
            return;
        }
        cache_list.emplace_front(key, value);
        key_to_iter[key] = cache_list.begin();
        if(key_to_iter.size() > capacity) {
            key_to_iter.erase(cache_list.back().first);
            cache_list.pop_back();
        }

    }
};

36、二叉树中序遍历

思路：递归法，中序遍历；迭代法，左子数不断入栈，然后不断出栈顶，如果有右子数便也压入栈，不然就不断出栈。

cpp 复制代码

// 递归
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        Traversal(root, res);
        return res;
    }

    void Traversal(TreeNode* root, vector<int> &res){
        if(root == nullptr)
            return;
        Traversal(root->left, res);
        res.push_back(root->val);
        Traversal(root->right, res);
    }
};

// 迭代
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;
        while(root || !stk.empty()){
            while(root){
                stk.push(root);
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            res.push_back(root->val);
            root = root->right;
        }
        return res;
    }
};

37、二叉树最大深度

思路：递归，从下而上统计左侧和右侧的深度再作比较，再往上传递。

cpp 复制代码

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(!root)
            return 0;
        int left_max = maxDepth(root->left);
        int right_max = maxDepth(root->right);
        return max(left_max, right_max) + 1;
    }
};

38、翻转二叉树

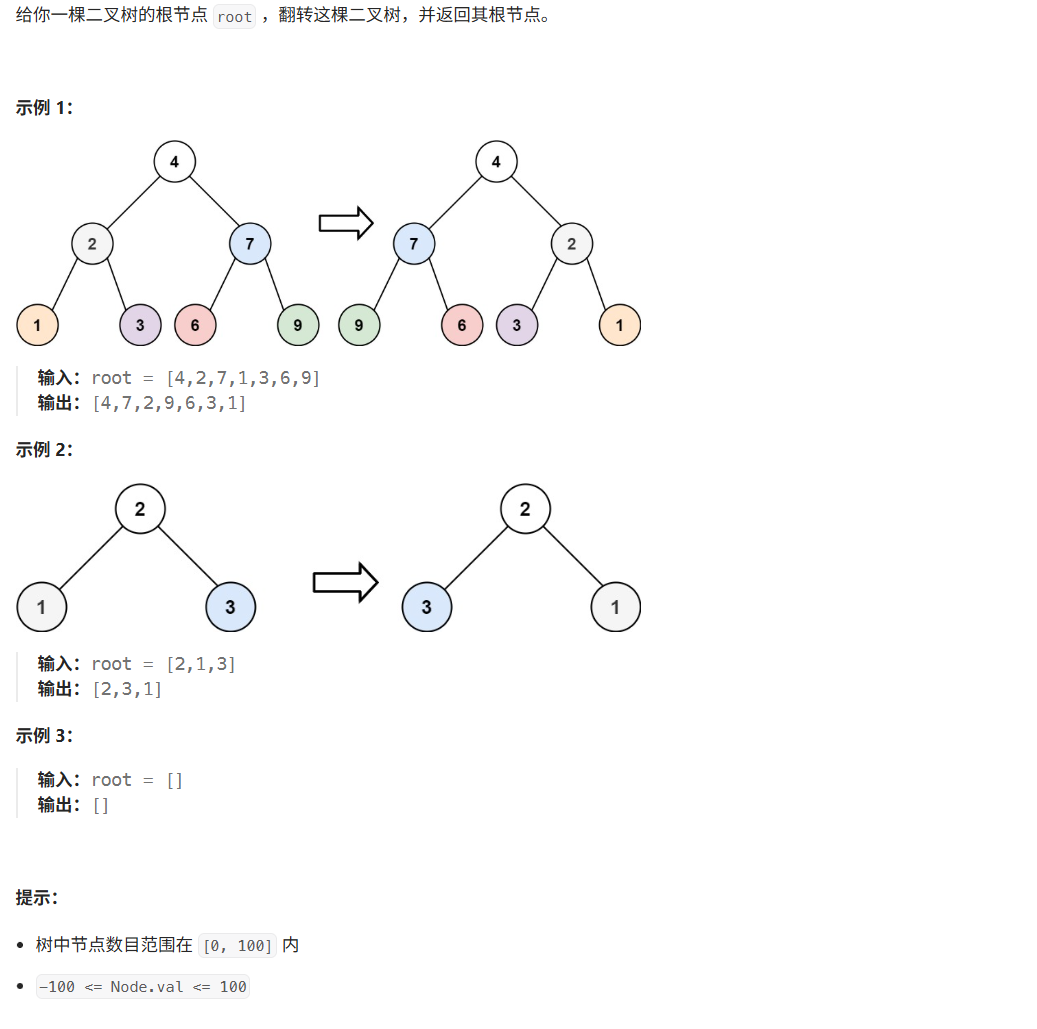思路：递归，每次获取子节点左右子节点，呼唤即可。

cpp 复制代码

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (!root) return nullptr;

        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);

        root->left = right;
        root->right = left;
        
        return root;
    }
};

39、对称二叉树

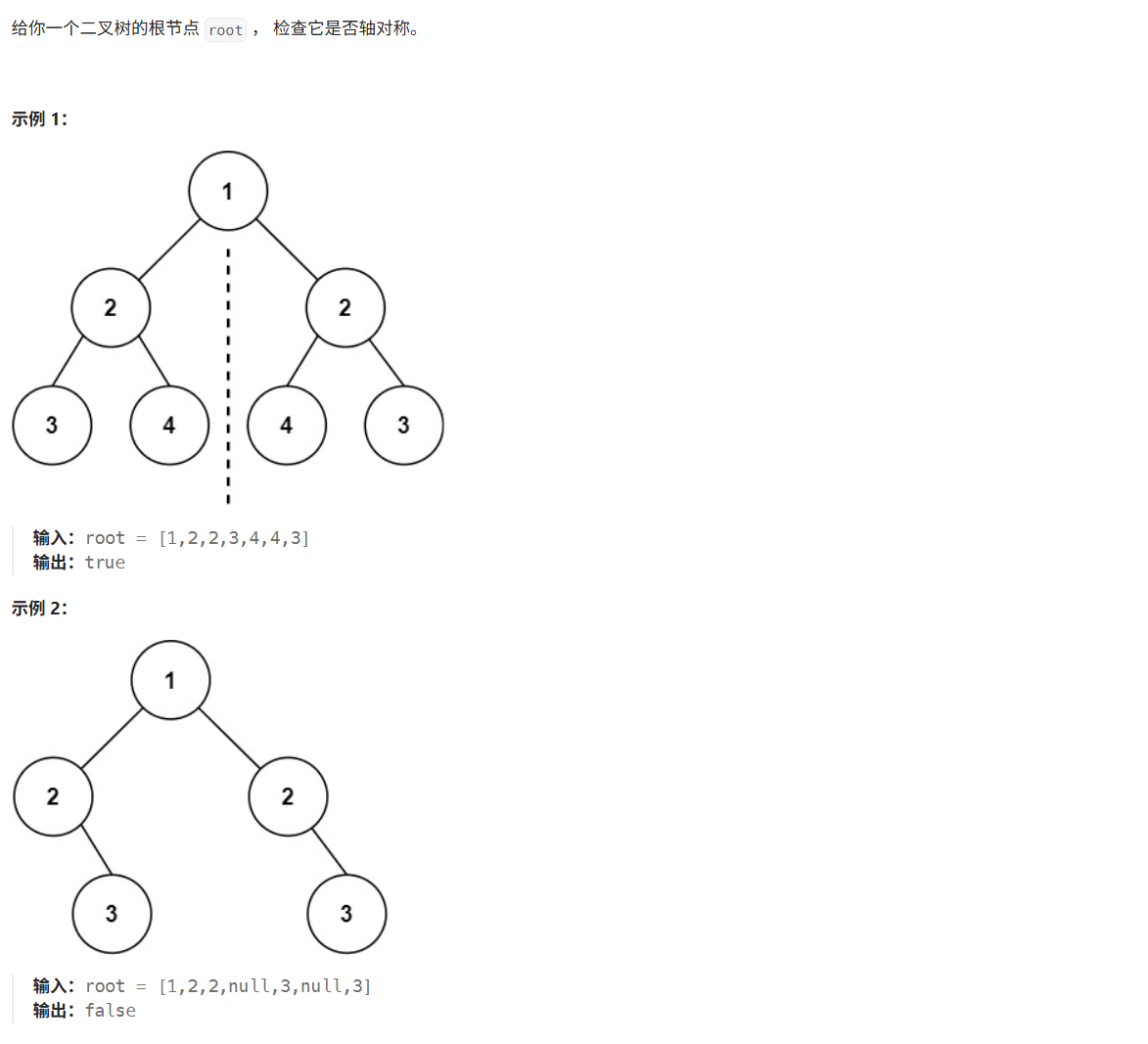
思路：递归法，自下而上，判断左子节点和右子节点、左子节点的左子节点和右子节点的右子节点、左子节点的右子节点和右子节点的左子节点的值是否相同。同时可以采用迭代法层序遍历判断回文数组，不过注意如果是有子节点空节点需要添加标记。

cpp 复制代码

// 递归法
class Solution {
    bool isSameTree(TreeNode* p, TreeNode* q){
        if(q == nullptr || p == nullptr)
            return p == q;

        if(!isSameTree(q->left, p->right))
            return false;
        if(!isSameTree(q->right, p->left))
            return false;
        if(p->val != q->val)
            return false;
        
        return true;

    }


public:
    bool isSymmetric(TreeNode* root) {
        return isSameTree(root->left, root->right);
    }
};

// 迭代法
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(!root) return true;

        deque<TreeNode*> dq = {root};
        while(!dq.empty()){  
            vector<int> val;
            int n = dq.size();
            while(n--){
                TreeNode* node = dq.front();
                dq.pop_front();
                if(!node){
                    val.push_back(INT_MIN);
                }else{
                    val.push_back(node->val);
                    dq.push_back(node->left);
                    dq.push_back(node->right);
                }            
            }
            vector<int> now = val;
            reverse(val.begin(), val.end());
            if(now != val) return false;
        }
        return true;
    }
};

40、二叉树的直径

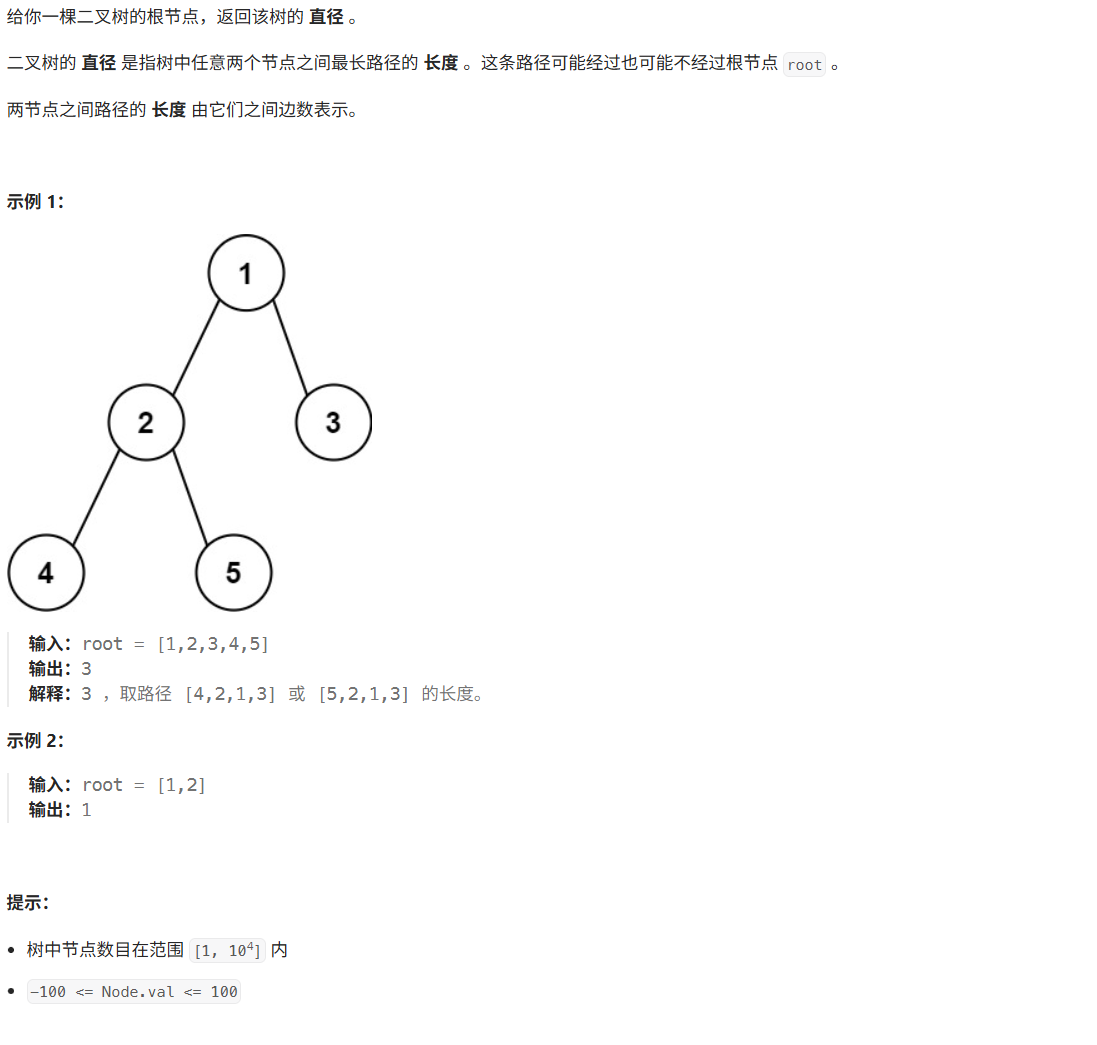
思路：和二叉树最大深度类似，只是这次统计是左侧+右侧深度之和的最大值。

cpp 复制代码

class Solution {
public:
    int ans = 0;

    int diameterOfBinaryTree(TreeNode* root) {
        if(!root) return 0;
        maxDepth(root);
        return ans;
    }

    int maxDepth(TreeNode* root) {
        if(!root) return 0;
        int left_max = maxDepth(root->left);
        int right_max = maxDepth(root->right);
        ans = max(left_max + right_max, ans);
        return max(left_max, right_max) + 1;
    }
};

41、二叉树层序遍历

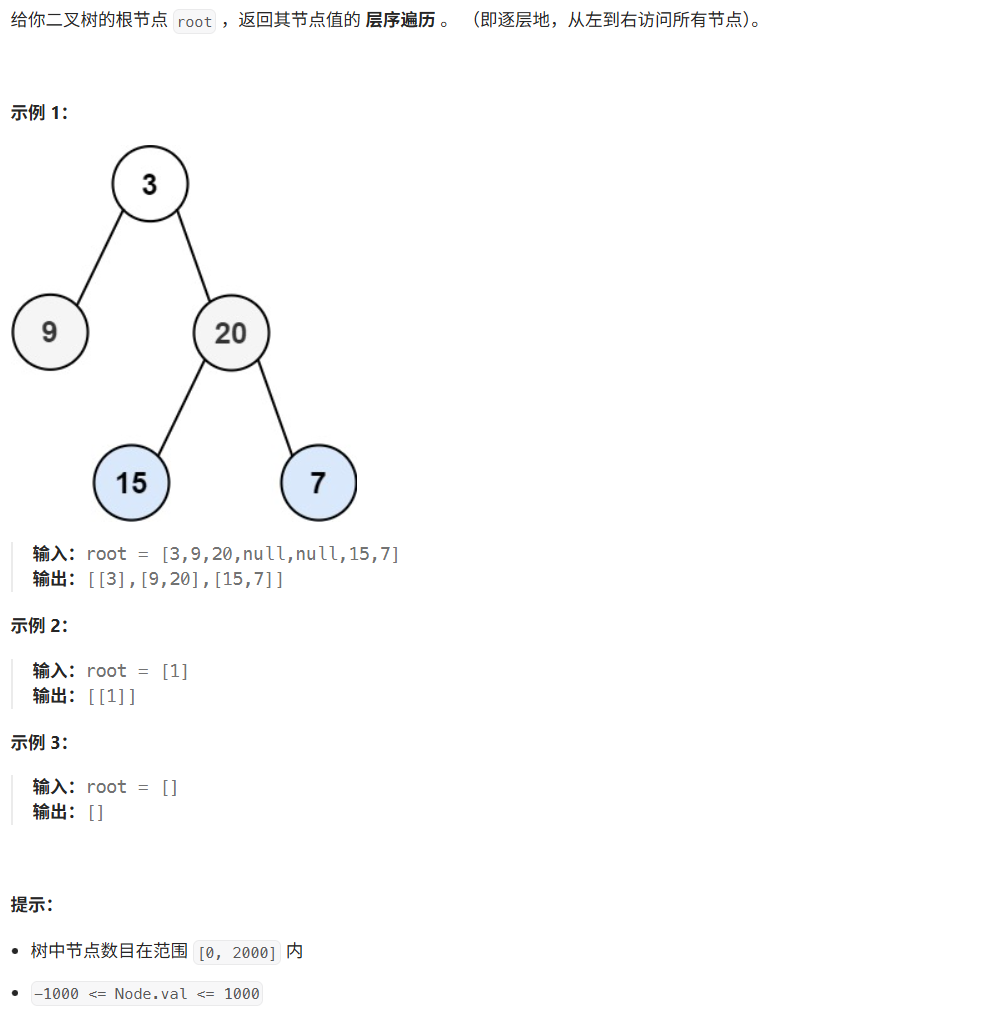
思路：递归法，每次递归向深度对应的数组添加节点值，再向左节点和右节点递归。迭代法，使用双向队列存储每层的节点，记录每层每个节点的值；记录一个节点的值后，把其左节点和右节点（如果有）加到双向队列，再删除双向队列里的原节点，以此循环直到双向队列为空。

cpp 复制代码

// 递归
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        pre(root, 0, ans);
        return ans;
    }

    void pre(TreeNode* root, int depth, vector<vector<int>>& ans){
        if(!root)
            return;
        if(depth >= ans.size())
            ans.push_back(vector<int> {});
        
        ans[depth].push_back(root->val);
        pre(root->left, depth + 1, ans);
        pre(root->right, depth + 1, ans);
    }
};


//迭代
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root){
        if(!root) return vector<vector<int>>{};
        vector<vector<int>> ans;
        deque<TreeNode*> dq = {root};
        while(!dq.empty()){
            vector<int> val;
            int n = dq.size();
            while(n--){
                TreeNode* node = dq.front();
                dq.pop_front();
                val.push_back(node->val);
                if(node->left) dq.push_back(node->left);
                if(node->right) dq.push_back(node->right);
            }            
            ans.push_back(val);
        }
        return ans;
    }
};