INT301 Bio-computation 生物计算（神经网络）Pt.10 联想存储器与HOPFIELD网络

文章目录

[1. 联想记忆](#1. 联想记忆)
- [1.1 计算机内存的访问方式](#1.1 计算机内存的访问方式)
- [1.2 联想存储器（Associative Memory）和模式联想（Pattern Association）](#1.2 联想存储器（Associative Memory）和模式联想（Pattern Association）)
- - [1.2.1 联想存储器（Associative Memories）](#1.2.1 联想存储器（Associative Memories）)
  - [1.2.2 存储模式（Stored Patterns）](#1.2.2 存储模式（Stored Patterns）)
  - [1.2.3 简单的联想记忆](#1.2.3 简单的联想记忆)
  - - [1.2.3.1 示例1 异联想（Hetero-associative）记忆网络](#1.2.3.1 示例1 异联想（Hetero-associative）记忆网络)
    - [1.2.3.2 示例2 自联想（Auto-associative）记忆网络](#1.2.3.2 示例2 自联想（Auto-associative）记忆网络)
[2. Hopfield网络](#2. Hopfield网络)
- [2.1 Hopfield网络的架构](#2.1 Hopfield网络的架构)
- [2.2 离散Hopfield网络的工作原理](#2.2 离散Hopfield网络的工作原理)
- [2.3 示例](#2.3 示例)
- [2.4 应用实例](#2.4 应用实例)
- [2.5 以三神经元的离散Hopfield网络为例](#2.5 以三神经元的离散Hopfield网络为例)
- - [2.5.1 更多示例：示例1 计算权重矩阵](#2.5.1 更多示例：示例1 计算权重矩阵)
  - [2.5.2 更多示例：示例2虚假状态（spurious state）](#2.5.2 更多示例：示例2虚假状态（spurious state）)
- [2.6 Hopfield网络的局限性](#2.6 Hopfield网络的局限性)

1. 联想记忆

1.1 计算机内存的访问方式

标准的计算机内存是通过分配的地址来访问的。内存中的每个存储单元都有一个唯一的地址，就像每个房子都有一个门牌号一样。CPU（中央处理器）可以通过这些地址来找到并操作内存中的数据。

当用户在计算机上搜索一个文件时，CPU需要将用户的请求（比如文件名等）转换成一个具体的数值指令。然后，CPU会在内存中搜索与该指令对应的地址，找到对应的文件数据。这个过程就像是根据门牌号找到具体的房子一样，CPU通过地址来定位内存中的数据。

计算机的内存通常被称为RAM。它的特点是随机存取，即可以随机地读写内存中的任何位置，而不需要按顺序访问。这使得CPU可以快速地获取和存储数据，从而提高计算机的运行效率。RAM是一种易失性存储器，当计算机断电后，存储在RAM中的数据会丢失。

1.2 联想存储器（Associative Memory）和模式联想（Pattern Association）

联想存储器（Associative Memory）是一种内容可寻址的结构。这意味着它可以根据存储内容本身来访问数据，而不是通过传统的物理地址来访问。

也就是说，你可以直接提供一个数据模式（pattern），存储器会自动找到与这个模式匹配的内容并返回。

例如，如果你在联想存储器中存储了一些用户的个人信息，当你提供一个用户的姓名时，存储器可以直接找到与这个姓名相关的所有信息，而不需要知道这些信息存储在哪个具体的地址上。

联想存储器通常与模式联想（Pattern Association）密切相关。联想存储器的核心功能是通过输入模式来找到相关的输出模式，这种功能的基础就是模式联想。

模式联想的类型有很多：

相似性（Similarity）：联想存储器可以将相似的模式关联起来。例如，如果你输入一个模式"苹果"，它可能会联想出"橙子"或"香蕉"，因为这些模式在语义或特征上是相似的。
对比性（Contrary）：联想存储器也可以将相反的模式关联起来。例如，"热"和"冷"、"高"和"低"等。
空间接近性（Spatial Proximity）：如果两个模式在空间上接近，联想存储器可以将它们关联起来。例如，在图像识别中，相邻的像素或物体特征可能会被关联。
时间连续性（Temporal Succession）：如果两个模式在时间上连续出现，联想存储器也可以将它们关联起来。例如，在视频或音频处理中，连续的帧或音符可能会被关联。

联想回忆（Associative Recall）是联想存储器的一个重要功能，它允许用户通过部分模式或不完整的模式来回忆完整的模式。具体来说：

唤起相关模式（Evoke Associated Patterns）：当你提供一个模式时，联想存储器可以唤起与之相关的其他模式。例如，输入"苹果"，可能会唤起"水果"、"红色"、"甜"等相关的模式。
通过部分模式回忆（Recall a Pattern by Part of It）：即使你只提供了一个模式的一部分，联想存储器也可以回忆出完整的模式。例如，你只输入"苹"，它也可以回忆出"苹果"。
处理不完整或噪声模式（Evoke/Recall with Incomplete/Noisy Patterns）：联想存储器的一个强大特性是它能够处理不完整或带有噪声的输入模式。即使输入的模式不完整或有错误，它仍然可以找到最接近的匹配模式并回忆出完整的模式。例如，输入"aple"（拼写错误），它仍然可以回忆出"苹果"。

1.2.1 联想存储器（Associative Memories）

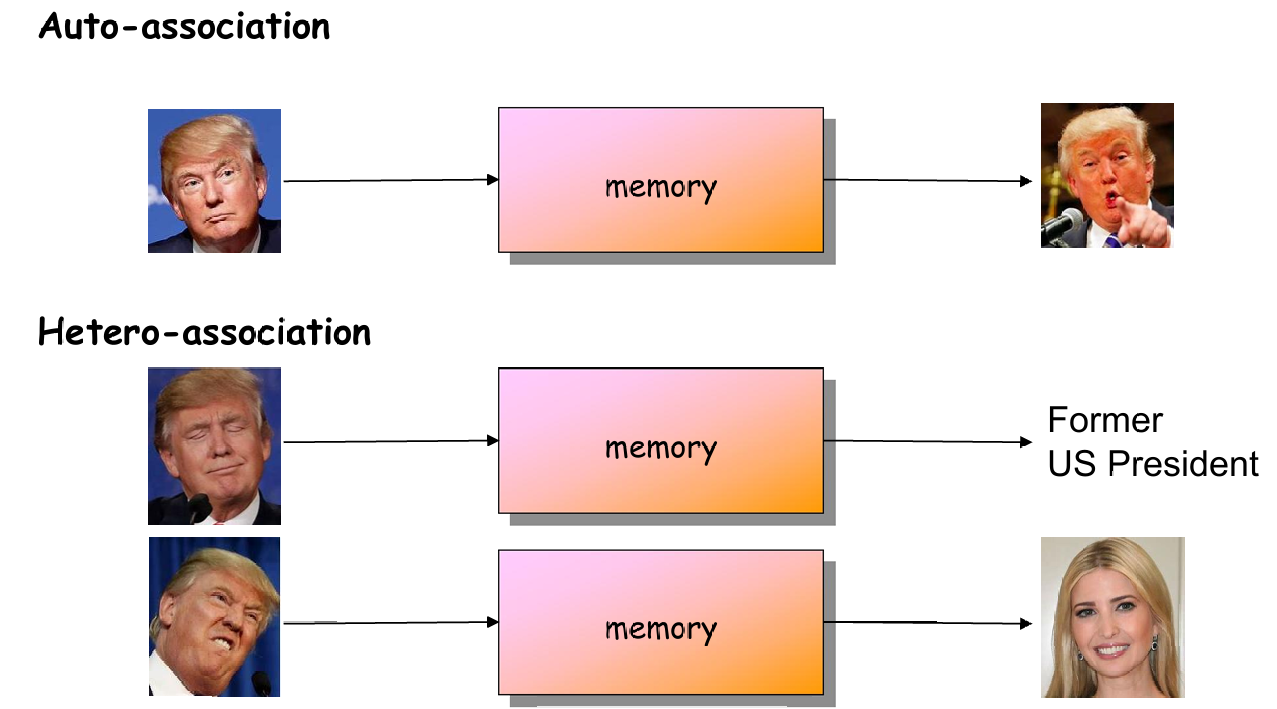
联想存储器（Associative Memories）有两种主要类型：自联想（Auto-associative）和异联想（Hetero-associative）。

自联想存储器（Auto-associative Memory）：
定义：自联想存储器是一种特殊的联想存储器，它的输入模式和输出模式是相同的。也就是说，它主要用于回忆和恢复之前存储的模式。
功能：当输入一个模式时，自联想存储器会检索出之前存储的、最接近当前输入模式的完整模式。这种存储器的主要用途是纠正输入错误或补充不完整的输入模式。
举例：
假设你存储了一个模式"apple"，然后输入了一个不完整的模式"apl"。自联想存储器会识别出"apl"与"apple"最接近，并返回完整的"apple"。
这种存储器在数据纠错、图像修复（如修复损坏的图像）和记忆恢复（如回忆模糊的记忆）等场景中非常有用。
异联想存储器（Hetero-associative Memory）：
定义：异联想存储器的输入模式和输出模式是不同的。它不仅在内容上不同，而且可能在类型和格式上也不同。
功能：这种存储器的主要作用是根据输入模式关联到一个完全不同的输出模式。输入模式和输出模式之间存在一种预定义的映射关系。
举例：
假设你输入一个模式"apple"，异联想存储器可能会返回一个完全不同的模式，比如"fruit"或"red"。
输入模式可以是一个单词，输出模式可以是一个图像；或者输入模式是一个图像，输出模式可以是一段文字描述。这种灵活性使得异联想存储器在多种应用中非常有用，如图像识别、自然语言处理和数据库查询。

下图也展示了两者的区别。

1.2.2 存储模式（Stored Patterns）

下图展示了一组存储的模式对。这些模式对是预先存储在联想记忆中的数据。

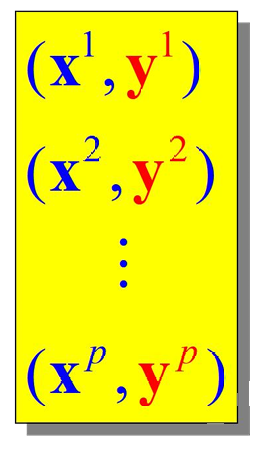
x i x^i xi和 y i y^i yi分别表示输入模式和输出模式。
x i ∈ R n x^i∈R^n xi∈Rn，这表示输入模式 x i x^i xi是一个 n n n维实数向量。
y i ∈ R n y^i∈R^n yi∈Rn，这表示输出模式 y i y^i yi是一个 n n n维实数向量。

自联想（Autoassociative）：

自联想记忆的定义为 x i ≡ y i x^i \equiv y^i xi≡yi

异联想（Heteroassociative）：

异联想记忆的定义为 x i ≠ y i x^i \neq y^i xi=yi

1.2.3 简单的联想记忆

下面展示一个简单的联想记忆网络。

这个简单的联想记忆网络是一个单层网络。它包含非线性单元，只有一个输入层。

这个结构类似于用于分类的简单神经网络。

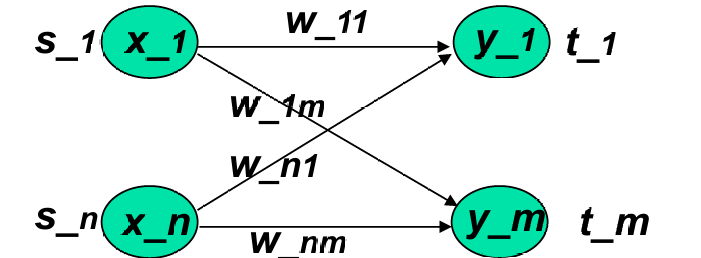
学习的目标有：

权重集合：学习的目标是获得一组权重 w i j w_{ij} wij。
训练模式对：这些权重是从一组训练模式对 s : t {s:t} s:t中学习得到的。
输入输出关系：当输入模式 s s s应用于输入层时，输出层会计算出 t t t。

这里的算法类似于Hebbian学习，Hebbian学习是一种神经科学理论，强调"一起激活的神经元会连接在一起"。在这种学习方式中，如果两个神经元同时激活，它们之间的连接会得到加强。

算法适用于处理二值（0或1）或双极（-1或1）模式。

对于每个训练样本 s : t s:t s:t ，权重的更新量 Δ w i j Δw_{ij} Δwij由输入 s i s_i si 和输出 t j t_j tj的乘积决定，即 Δ w i j = s i ⋅ t j Δw_{ij}=s_i⋅t_j Δwij=si⋅tj

如果输入和输出都是1（二值）或具有相同符号（双极），则 Δ w i j Δw_{ij} Δwij增加，这意味着权重会增加。

如果 Δ w i j Δw_{ij} Δwij最初为0，那么在所有 P P P个训练模式更新后，权重 Δ w i j Δw_{ij} Δwij可以通过以下公式计算： w i j = ∑ p = 1 P s i ( p ) t j ( p ) w_{ij} = \sum_{p=1}^{P} s_i(p) t_j(p) wij=∑p=1Psi(p)tj(p)

其中 s i ( p ) s_i(p) si(p)和 t j ( p ) t_j(p) tj(p)分别是第 p p p个训练样本的输入和输出。

所有权重 w i j w_{ij} wij组成权重矩阵 W = { w i j } W = \{ w_{ij} \} W={wij}

这是直接计算得到的，而不是通过迭代更新来获得权重 W W W，可以直接从训练集中计算出权重，方法是计算输入向量 s s s和目标向量 t t t的外积（outer product）。

外积是两个向量的乘积，结果是一个矩阵。如果 s s s和 t t t是行向量，那么它们的外积 s T ( p ) ⊗ t ( p ) s^T(p) \otimes t(p) sT(p)⊗t(p)是一个矩阵，其中每个元素是 s s s和 t t t对应元素的乘积。
Δ W ( p ) = s T ( p ) ⊗ t ( p ) = [ s 1 ⋮ s n ] [ t 1 ⋯ t m ] = [ s 1 t 1 ⋯ s 1 t m ⋮ ⋱ ⋮ s n t 1 ⋯ s n t m ] = [ Δ w 11 ⋯ Δ w 1 m ⋮ ⋱ ⋮ Δ w n 1 ⋯ Δ w n m ] \Delta W(p) = s^T(p) \otimes t(p) = \begin{bmatrix} s_1 \\ \vdots \\ s_n \end{bmatrix} \begin{bmatrix} t_1 & \cdots & t_m \end{bmatrix} = \begin{bmatrix} s_1 t_1 & \cdots & s_1 t_m \\ \vdots & \ddots & \vdots \\ s_n t_1 & \cdots & s_n t_m \end{bmatrix} = \begin{bmatrix} \Delta w_{11} & \cdots & \Delta w_{1m} \\ \vdots & \ddots & \vdots \\ \Delta w_{n1} & \cdots & \Delta w_{nm} \end{bmatrix} ΔW(p)=sT(p)⊗t(p)= s1⋮sn [t1⋯tm]= s1t1⋮snt1⋯⋱⋯s1tm⋮sntm = Δw11⋮Δwn1⋯⋱⋯Δw1m⋮Δwnm

权重矩阵 W W W可以通过对所有训练样本的外积求和得到： W ( P ) = ∑ p = 1 P s T ( p ) ⊗ t ( p ) W(P) = \sum_{p=1}^{P} s^T(p) \otimes t(p) W(P)=∑p=1PsT(p)⊗t(p)

这意味着对于每个训练样本 p ，计算其外积，然后将所有外积相加。

计算过程涉及到三个嵌套循环：
p = 1 p=1 p=1到 P P P：遍历每个训练样本。
i = 1 i=1 i=1到 n n n：遍历权重矩阵 W W W的每一行。
j = 1 j=1 j=1到 m m m：遍历权重矩阵 W W W的每一列。

对于每个元素 w i j w_{ij} wij ，更新公式为： w i j : = w i j + s i ( p ) ⋅ t j ( p ) w_{ij} := w_{ij} + s_i(p) \cdot t_j(p) wij:=wij+si(p)⋅tj(p)

这意味着每个权重 w i j w_{ij} wij是通过累加每个训练样本中对应输入和目标值的乘积得到的。

这种模型能否提供良好的关联性呢？

使用训练样本（在权重学习或计算之后）。

将输入样本 s ( k ) s(k) s(k)应用到单层网络，希望输出 t ( k ) t(k) t(k)出现在另一端，即 f ( s ( k ) W ) = t ( k ) f(s(k)W)=t(k) f(s(k)W)=t(k)。
s ( k ) W = s ( k ) ∑ p = 1 P s T ( p ) t ( p ) = ∑ p = 1 P s ( k ) s T ( p ) t ( p ) s(k)W = s(k) \sum_{p=1}^{P} s^T(p)t(p) = \sum_{p=1}^{P} s(k)s^T(p)t(p) s(k)W=s(k)∑p=1PsT(p)t(p)=∑p=1Ps(k)sT(p)t(p)

这表示将输入样本 s ( k ) s(k) s(k)与权重矩阵 W W W相乘，权重矩阵是由所有训练样本的外积之和构成的。
= s ( k ) s T ( k ) t ( k ) + ∑ p ≠ k s ( k ) s T ( p ) t ( p ) = s(k)s^T(k)t(k) + \sum_{p \neq k} s(k)s^T(p)t(p) =s(k)sT(k)t(k)+∑p=ks(k)sT(p)t(p)

这表示输出可以分解为两部分：

主要项（principal term）： s ( k ) s T ( k ) t ( k ) s(k)s^T(k)t(k) s(k)sT(k)t(k)，这是输入样本 s ( k ) s(k) s(k)与自身对应的目标样本 t ( k ) t(k) t(k)的乘积。

串扰项（cross-talk term）： ∑ p ≠ k s ( k ) s T ( p ) t ( p ) \sum_{p \neq k} s(k)s^T(p)t(p) ∑p=ks(k)sT(p)t(p)，这是输入样本 s ( k ) s(k) s(k)与其它所有目标样本 t ( p ) t(p) t(p)的乘积之和。

进一步简化：
= ∥ s ( k ) ∥ 2 t ( k ) + ∑ p ≠ k s ( k ) s T ( p ) t ( p ) = \|s(k)\|^2 t(k) + \sum_{p \neq k} s(k)s^T(p)t(p) =∥s(k)∥2t(k)+∑p=ks(k)sT(p)t(p)

其中， ∥ s ( k ) ∥ 2 \|s(k)\|^2 ∥s(k)∥2是输入样本 s ( k ) s(k) s(k)的范数平方。

由于每个权重包含了所有样本的一些信息（也就是串扰项），因此可能不总是成功。

我们再仔细分析一下。

主项（Principal Term）：

主项表示输入样本 s ( k ) s(k) s(k)与其对应目标样本 t ( k ) t(k) t(k)之间的关联。

这是我们希望在联想记忆中实现的主要功能，即当输入 s ( k ) s(k) s(k)时，能够正确地回忆起 t ( k ) t(k) t(k)。

串扰（Cross-talk）：

串扰表示输入样本 s ( k ) s(k) s(k)与其对应目标样本 t ( k ) t(k) t(k)与其他训练样本对之间的相关性。

当串扰较大时，输入 s ( k ) s(k) s(k)可能会错误地回忆起除 t ( k ) t(k) t(k)之外的其他信息。

串扰可能导致联想记忆的性能下降，因为它引入了不期望的关联。

如果所有的输入样本 s ( p ) s(p) s(p)两两正交，即对于任意 p ≠ k p \neq k p=k，有 s ( k ) ⋅ s ( p ) = 0 s(k)⋅s(p)=0 s(k)⋅s(p)=0，则没有除了 s ( k ) : t ( k ) s(k):t(k) s(k):t(k)之外的样本对结果产生贡献。

在这种情况下，串扰为零，因为不同样本之间没有相关性，从而提高了联想记忆的准确性。

在一个 n n n维空间中，最多只能有 n n n个正交向量。

因此当训练样本数量 P P P超过 n n n时，不可能所有样本都是正交的，从而增加了串扰。

随着训练样本数量 P P P的增加，串扰也会增加，因为更多的样本意味着更多的潜在相关性，这可能导致错误的联想。

1.2.3.1 示例1 异联想（Hetero-associative）记忆网络

这里是二进制模式对，输入模式 s s s的长度 ∣ s ∣ = 4 ∣s∣=4 ∣s∣=4 ，输出模式 t t t的长度 ∣ t ∣ = 2 ∣t∣=2 ∣t∣=2 。

输出单元的总加权输入计算公式为 y i n j = ∑ i x i w i j y_{in_j} = \sum_i x_i w_{ij} yinj=∑ixiwij，其中 x i x_i xi是输入单元的值， w i j w_{ij} wij是从输入单元 i i i到输出单元 j j j的权重。

使用阈值激活函数
y j = { 1 if y i n j > 0 0 if y i n j ≤ 0 y_j = \begin{cases} 1 & \text{if } y_{in_j} > 0 \\ 0 & \text{if } y_{in_j} \leq 0 \end{cases} yj={10if yinj>0if yinj≤0

权重矩阵 W W W 是所有训练样本对的外积之和，即
W = ∑ p = 1 P s i T ( p ) t j ( p ) W = \sum_{p=1}^{P} s_i^T(p) t_j(p) W=∑p=1PsiT(p)tj(p)

其中 s i T ( p ) s_i^T(p) siT(p)是第 p p p个训练样本的输入模式的转置， t j ( p ) t_j(p) tj(p)是第 p p p个训练样本的输出模式。

训练样本示例：给出了四个训练样本对，每个样本对包含一个输入模式 s ( p ) s(p) s(p)和一个输出模式 t ( p ) t(p) t(p)

p = 1 p=1 p=1: s ( p ) = ( 1 0 0 0 ) s(p) = (1\ 0\ 0\ 0) s(p)=(1 0 0 0), t ( p ) = ( 1 , 0 ) t(p) = (1, 0) t(p)=(1,0)
p = 2 p=2 p=2: s ( p ) = ( 1 1 0 0 ) s(p) = (1\ 1\ 0\ 0) s(p)=(1 1 0 0), t ( p ) = ( 1 , 0 ) t(p) = (1, 0) t(p)=(1,0)
p = 3 p=3 p=3: s ( p ) = ( 0 0 0 1 ) s(p) = (0\ 0\ 0\ 1) s(p)=(0 0 0 1), t ( p ) = ( 0 , 1 ) t(p) = (0, 1) t(p)=(0,1)
p = 4 p=4 p=4: s ( p ) = ( 0 0 1 1 ) s(p) = (0\ 0\ 1\ 1) s(p)=(0 0 1 1), t ( p ) = ( 0 , 1 ) t(p) = (0, 1) t(p)=(0,1)

然后我们计算外积。
s T ( 1 ) ⊗ t ( 1 ) = [ 1 0 0 0 ] [ 1 0 ] = [ 1 0 0 0 0 0 0 0 ] s^T(1) \otimes t(1) = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} \begin{bmatrix} 1 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{bmatrix} sT(1)⊗t(1)= 1000 [10]= 10000000
s T ( 2 ) ⊗ t ( 2 ) = [ 1 1 0 0 ] [ 1 0 ] = [ 1 0 1 0 0 0 0 0 ] s^T(2) \otimes t(2) = \begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} \begin{bmatrix} 1 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 0 \\ 0 & 0 \end{bmatrix} sT(2)⊗t(2)= 1100 [10]= 11000000
s T ( 3 ) ⊗ t ( 3 ) = [ 0 0 0 1 ] [ 0 1 ] = [ 0 0 0 0 0 0 0 1 ] s^T(3) \otimes t(3) = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} \begin{bmatrix} 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 1 \end{bmatrix} sT(3)⊗t(3)= 0001 [01]= 00000001
s T ( 4 ) ⊗ t ( 4 ) = [ 0 0 1 1 ] [ 0 1 ] = [ 0 0 0 0 1 0 1 0 ] s^T(4) \otimes t(4) = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \end{bmatrix} \begin{bmatrix} 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 1 & 0 \\ 1 & 0 \end{bmatrix} sT(4)⊗t(4)= 0011 [01]= 00110000

权重矩阵 W W W 是所有训练样本对的外积之和，即
W = ∑ p = 1 P s i T ( p ) t j ( p ) W = \sum_{p=1}^{P} s_i^T(p) t_j(p) W=∑p=1PsiT(p)tj(p)，所以 W = [ 2 0 1 0 0 1 0 2 ] W = \begin{bmatrix} 2 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 2 \end{bmatrix} W= 21000012

然后我们对新的输入模式进行分类。

输入模式 x = ( 1 0 0 0 ) x=(1\ 0\ 0\ 0) x=(1 0 0 0)：

我们先计算 x W xW xW：

1 0 0 0 \] \[ 2 0 1 0 0 1 0 2 \] = \[ 2 0 \] \\begin{bmatrix} 1 \& 0 \& 0 \& 0 \\end{bmatrix} \\begin{bmatrix} 2 \& 0 \\\\ 1 \& 0 \\\\ 0 \& 1 \\\\ 0 \& 2 \\end{bmatrix} = \\begin{bmatrix} 2 \& 0 \\end{bmatrix} \[1000\] 21000012 =\[20

应用激活函数（阈值函数）：

结果为 y 1 = 1 , y 2 = 0 y_1 = 1, \quad y_2 = 0 y1=1,y2=0

输入模式 x = ( 0 1 0 0 ) x=(0\ 1\ 0\ 0) x=(0 1 0 0)：

我们先计算 x W xW xW：

0 1 0 0 \] \[ 2 0 1 0 0 1 0 2 \] = \[ 1 0 \] \\begin{bmatrix} 0 \& 1 \& 0 \& 0 \\end{bmatrix} \\begin{bmatrix} 2 \& 0 \\\\ 1 \& 0 \\\\ 0 \& 1 \\\\ 0 \& 2 \\end{bmatrix} = \\begin{bmatrix} 1 \& 0 \\end{bmatrix} \[0100\] 21000012 =\[10

应用激活函数（阈值函数）：

结果为 y 1 = 1 , y 2 = 0 y_1 = 1, \quad y_2 = 0 y1=1,y2=0

这个输入模式与训练样本 s ( 1 ) s(1) s(1)和 s ( 2 ) s(2) s(2)类似。

输入模式 x = ( 0 1 1 0 ) x=(0\ 1\ 1\ 0) x=(0 1 1 0)：

我们先计算 x W xW xW：

0 1 1 0 \] \[ 2 0 1 0 0 1 0 2 \] = \[ 1 1 \] \\begin{bmatrix} 0 \& 1 \& 1 \& 0 \\end{bmatrix} \\begin{bmatrix} 2 \& 0 \\\\ 1 \& 0 \\\\ 0 \& 1 \\\\ 0 \& 2 \\end{bmatrix} = \\begin{bmatrix} 1 \& 1 \\end{bmatrix} \[0110\] 21000012 =\[11

应用激活函数（阈值函数）：

结果为 y 1 = 1 , y 2 = 1 y_1 = 1, \quad y_2 = 1 y1=1,y2=1

输入模式 (0 1 1 0) 没有足够相似于任何已定义的类别，因为它同时激活了两个输出。

1.2.3.2 示例2 自联想（Auto-associative）记忆网络

自联想网络与异联想网络类似，但不同之处在于自联想网络的输出 t ( p ) t(p) t(p)等于输入 s ( p ) s(p) s(p)。

自联想网络用于通过输入模式的噪声或不完整版本来回忆或恢复原始模式。

使用阈值激活函数
y j = { 1 if y i n j > 0 0 if y i n j = 0 − 1 if y i n j < 0 y_j = \begin{cases} 1 & \text{if } y_{in_j} > 0 \\ 0 & \text{if } y_{in_j} = 0 \\ -1 & \text{if } y_{in_j} < 0 \end{cases} yj=⎩ ⎨ ⎧10−1if yinj>0if yinj=0if yinj<0

一个单一的模式 s = ( 1 , 1 , 1 , − 1 ) s=(1,1,1,−1) s=(1,1,1,−1)被存储，权重通过外积计算得到，这里输出和输入相等，所以是 s ⊗ s s⊗s s⊗s。
W = [ 1 1 1 − 1 1 1 1 − 1 1 1 1 − 1 − 1 − 1 − 1 1 ] W = \begin{bmatrix} 1 & 1 & 1 & -1 \\ 1 & 1 & 1 & -1 \\ 1 & 1 & 1 & -1 \\ -1 & -1 & -1 & 1 \end{bmatrix} W= 111−1111−1111−1−1−1−11

我们现在有几种不同的输入情况，包括训练样本、噪声模式、信息确实和更噪声的模式。

训练样本：
输入： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)
计算： ( 1 1 1 − 1 ) W = ( 4 4 4 − 4 ) (1\ 1\ 1\ -1)W=(4\ 4\ 4\ -4) (1 1 1 −1)W=(4 4 4 −4)
因此输出： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)（正确恢复）
噪声模式：
输入： ( − 1 1 1 − 1 ) (-1\ 1\ 1\ -1) (−1 1 1 −1)
计算： ( − 1 1 1 − 1 ) W = ( 2 2 2 − 2 ) (-1\ 1\ 1\ -1)W=(2\ 2\ 2\ -2) (−1 1 1 −1)W=(2 2 2 −2)
输出： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)（成功从噪声中恢复）
信息缺失：
输入： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)
计算： ( 0 0 1 − 1 ) W = ( 2 2 2 − 2 ) (0\ 0\ 1\ -1)W=(2\ 2\ 2\ -2) (0 0 1 −1)W=(2 2 2 −2)
输出： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)（成功补全缺失信息）
更噪声的模式：
输入： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)
计算： ( − 1 − 1 1 − 1 ) W = ( 0 0 0 0 ) (-1\ -1\ 1\ -1)W=(0\ 0\ 0\ 0) (−1 −1 1 −1)W=(0 0 0 0)
输出： ( 0 0 0 0 ) (0\ 0\ 0\ 0) (0 0 0 0)（未能识别，输出为零向量）

W W W总是一个对称矩阵。这是因为在自联想网络中，权重矩阵是通过输入模式的外积计算得到的，外积的结果总是对称的。

当存储多个模式（即 P P P较大）时，对角线元素将在计算中占主导地位。这是因为每个模式的外积都会对对角线元素产生贡献，而这些贡献会累加。

当 P P P较大时， W W W会接近一个单位矩阵。这是因为每个模式的外积都会使 W W W的对角线元素增加，而其他元素相对不变，导致 W W W越来越接近单位矩阵。

当 W W W接近单位矩阵时，输出将等于输入。这意味着网络可能会失去模式纠正的能力，因为它只是简单地将输入复制到输出，而没有进行任何实质性的转换或恢复。

为了解决这个问题，可以将 W W W的对角线元素替换为零。这样可以防止对角线元素在计算中占主导地位，从而保持网络的模式纠正能力。

所以现在我们前面的例子的权重矩阵变为
W ′ = [ 0 1 1 − 1 1 0 1 − 1 1 1 0 − 1 − 1 − 1 − 1 0 ] W' = \begin{bmatrix} 0 & 1 & 1 & -1 \\ 1 & 0 & 1 & -1 \\ 1 & 1 & 0 & -1 \\ -1 & -1 & -1 & 0 \end{bmatrix} W′= 011−1101−1110−1−1−1−10

训练样本：
输入： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)
计算： ( 1 1 1 − 1 ) W ′ = ( 3 3 3 − 3 ) (1\ 1\ 1\ -1)W'=(3\ 3\ 3\ -3) (1 1 1 −1)W′=(3 3 3 −3)
因此输出： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)（正确恢复）
噪声模式：
输入： ( − 1 1 1 − 1 ) (-1\ 1\ 1\ -1) (−1 1 1 −1)
计算： ( − 1 1 1 − 1 ) W ′ = ( 3 1 1 − 1 ) (-1\ 1\ 1\ -1)W'=(3\ 1\ 1\ -1) (−1 1 1 −1)W′=(3 1 1 −1)
输出： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)（成功从噪声中恢复）
信息缺失：
输入： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)
计算： ( 0 0 1 − 1 ) W ′ = ( 2 2 1 − 1 ) (0\ 0\ 1\ -1)W'=(2\ 2\ 1\ -1) (0 0 1 −1)W′=(2 2 1 −1)
输出： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)（成功补全缺失信息）
更噪声的模式：
输入： ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)
计算： ( − 1 − 1 1 − 1 ) W ′ = ( 1 1 − 1 1 ) (-1\ -1\ 1\ -1)W'=(1\ 1\ -1\ 1) (−1 −1 1 −1)W′=(1 1 −1 1)
输出： ( 1 1 − 1 1 ) (1\ 1\ -1\ 1) (1 1 −1 1)（错误的结果）

2. Hopfield网络

Hopfield网络是一种受神经科学启发的计算模型，由加州理工学院的物理学家John Hopfield在1982年提出。

Hopfield网络是一个全连接的网络，意味着网络中的每个节点都与其他所有节点相连。

而且网络中的权重是对称的，即从节点A到节点B的权重与从节点B到节点A的权重相同。

在Hopfield网络中，每个节点既可以作为输入节点，也可以作为输出节点。

Hopfield网络的应用包括：

联想记忆（Associated memories）：Hopfield网络可以用于存储和回忆模式，类似于人脑的工作方式。它可以存储多个模式，并且即使输入模式有噪声或不完整，网络也能回忆起最接近的存储模式。
组合优化（Combinatorial optimization）：Hopfield网络可以用于解决组合优化问题，如旅行商问题（TSP）等。网络通过迭代更新节点状态来寻找问题的最优解。

John Hopfield对神经网络的主要贡献如下：

将网络视为动态系统：Hopfield将神经网络视为一个动态系统，这意味着网络的状态会随时间变化，直到达到一个稳定状态。
引入能量函数和吸引子（Attractors）：Hopfield引入了能量函数的概念，用于描述网络状态的能量。网络的目标是最小化这个能量函数。吸引子是指网络状态的稳定点，网络在迭代过程中会收敛到这些点。

Hopfield网络有两种形式：

离散（Discrete）：在离散Hopfield网络中，神经元的输出是二进制的，即每个神经元的输出只能是1或-1。
连续（Continuous）：在连续Hopfield网络中，神经元的输出可以是任意实数值。

我们只会聚焦于离散的Hopfield模型。因为离散Hopfield模型的数学描述更直接，更容易理解和分析，因此更受关注。

在离散Hopfield模型中，每个神经元的输出只能是1或-1，这与生物神经元的激活状态相似，即神经元要么激活（输出1），要么不激活（输出-1）。

在离散Hopfield模型的最简单的形式中，神经元的输出函数是符号函数。最简单的输出函数是符号函数（sign function），它对于大于等于0的参数返回1，对于小于0的参数返回-1。

2.1 Hopfield网络的架构

网络由一层神经元组成，这些神经元同时作为输入和输出。这意味着网络是完全连接的，每个神经元都与其他所有神经元相连。

网络中的节点是阈值单元，可以是二进制（0或1）或双极性（-1或1）。

网络中的权重是完全连接的，对称的，并且对角线上的权重为零。这意味着每个神经元与其他所有神经元之间的连接权重是相同的（ w i j = w j i w_{ij}=w_{ji} wij=wji），并且神经元与自身的连接权重为零（ w i i = 0 w_{ii}=0 wii=0）

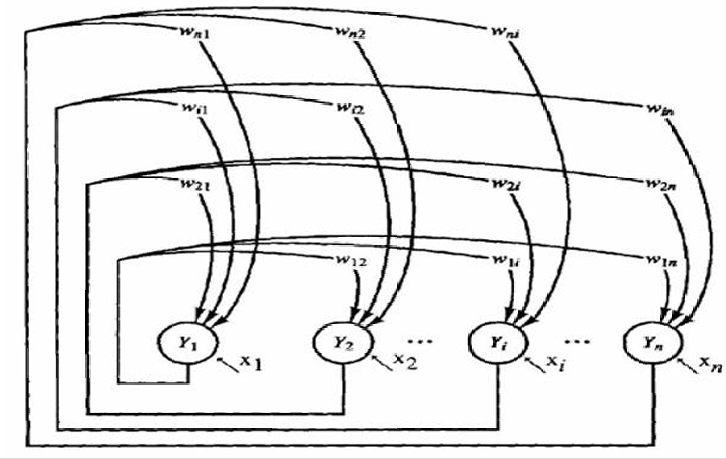
x i x_i xi表示外部输入，这些输入可以是暂时的或永久的。外部输入可以影响网络的状态，但网络的主要功能是通过内部连接和权重来存储和回忆信息。

下图展示的架构和上图同理到那时更加清晰。

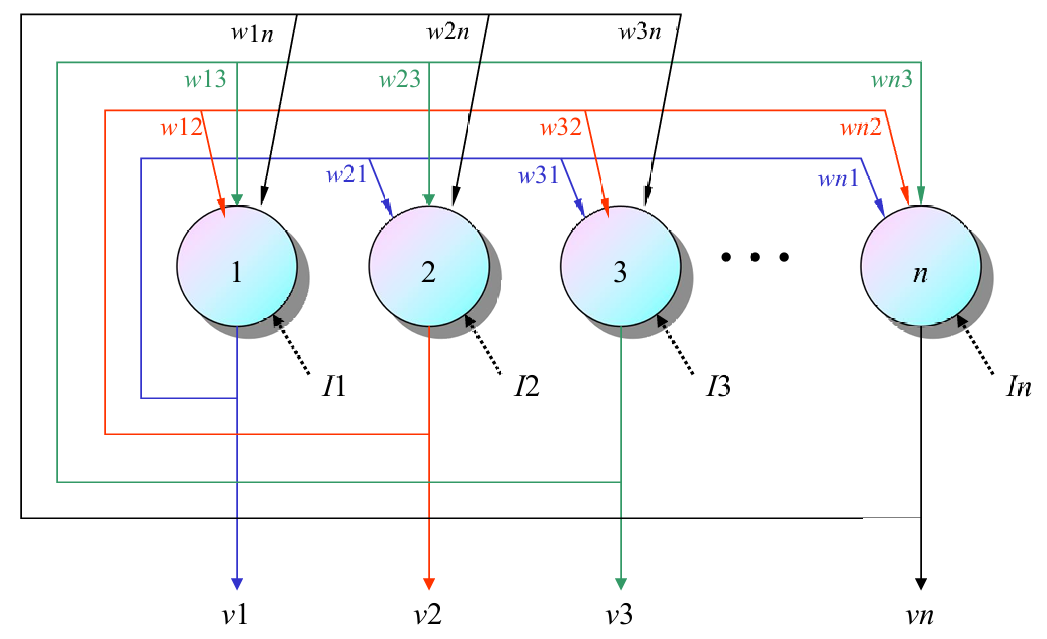
存储规则（Storage rule）：

权重 w i j w_{ij} wij按以下公式计算：
w i j = 1 N ∑ p = 1 P x i p x j p w_{ij} = \frac{1}{N} \sum_{p=1}^{P} x_i^p x_j^p wij=N1∑p=1Pxipxjp

其中， N N N是神经元数量，
P P P是存储的模式（patterns）数量，
x i p x_i^p xip表示第 p p p个模式的第 i i i个神经元状态（通常取 1 或 -1）。

权重矩阵是对称的，即 w i j = w j i w_{ij}=w_{ji} wij=wji。

神经元不与自身直接连接，即 w i i = 0 w_{ii}=0 wii=0。

在满足这些条件（对称权重、无自连接）的情况下，数学上可以证明网络在无限次迭代后会达到稳定的激活状态。

这里的"稳定状态"指的是网络的状态不再随迭代改变，通常对应于已存储的模式或它们的反转。

在离散Hopfield网络中，输入或输出向量的每个分量只能取1或-1的值。

在时间 t t t时，第 i i i个神经元的输出 v i ( t ) v_i(t) vi(t)是根据以下公式计算的：
v i ( t ) = sgn ( ∑ j = 1 N w i j v j ( t − 1 ) ) v_i(t) = \text{sgn}\left(\sum_{j=1}^{N} w_{ij} v_j(t-1)\right) vi(t)=sgn(∑j=1Nwijvj(t−1))

其中， sgn \text{sgn} sgn是符号函数，它返回输入值的符号： sgn ( x ) = { 1 if x > 0 − 1 if x ≤ 0 \text{sgn}(x) = \begin{cases} 1 & \text{if } x > 0 \\ -1 & \text{if } x \leq 0 \end{cases} sgn(x)={1−1if x>0if x≤0
w i j w_{ij} wij是权重矩阵中的元素，表示从第 j j j 个神经元到第 i i i个神经元的连接权重。
v j ( t − 1 ) v_j(t-1) vj(t−1)是在时间 t − 1 t-1 t−1时第 j j j个神经元的输出。
N N N是网络中神经元的总数。

这个计算是不断递归的。每次迭代都会更新所有神经元的输出，直到网络达到一个稳定状态，即输出不再发生变化。

在离散Hopfield网络中，当网络达到稳定状态时，意味着网络的输出不再随时间变化。换句话说，网络的激活模式（即神经元的状态）不再改变。

Hopfield网络将输入模式与自身关联，这意味着在每次迭代中，激活模式会被吸引到存储在网络中的某个模式。

随着迭代的进行，网络的激活模式会逐渐接近网络中存储的一个模式。

当网络收敛后，它最有可能呈现出它最初被初始化时存储的模式之一。

由于Hopfield网络能够将输入模式吸引到存储的模式，因此它可以用于恢复不完整或含有噪声的输入模式。这是Hopfield网络的一个重要应用，特别是在模式识别和记忆恢复方面。

2.2 离散Hopfield网络的工作原理

离散Hopfield网络通过输入向量来回忆存储的向量。

回忆（Recall）：

使用输入向量：通过提供一个输入向量，网络可以回忆起与之最匹配的存储向量。
随机选择更新单元：每次迭代中，随机选择一个神经元进行更新。这是一种异步更新方式，与传统的同步更新不同。
周期性检查收敛：在更新过程中，网络会定期检查是否达到了稳定状态，即输出不再变化。

异步模式更新规则（Asynchronous Mode Update Rule）： H i ( t + 1 ) = ∑ j = 1 , j ≠ i n w i j v j ( t ) + I i H_i(t+1) = \sum_{j=1, j \neq i}^{n} w_{ij} v_j(t) + I_i Hi(t+1)=∑j=1,j=inwijvj(t)+Ii

其中 H i ( t + 1 ) H_i(t+1) Hi(t+1)是第 i i i个神经元在 t + 1 t+1 t+1时刻的净输入， w i j w_{ij} wij是权重， v j ( t ) v_j(t) vj(t)是第 j j j个神经元在 t t t时刻的输出， I i I_i Ii是第 i i i个神经元的输入偏置。

输出更新：
v i ( t + 1 ) = sgn [ H i ( t + 1 ) ] = { 1 if H i ( t + 1 ) ≥ 0 − 1 if H i ( t + 1 ) < 0 v_i(t+1) = \text{sgn}[H_i(t+1)] = \begin{cases} 1 & \text{if } H_i(t+1) \geq 0 \\ -1 & \text{if } H_i(t+1) < 0 \end{cases} vi(t+1)=sgn[Hi(t+1)]={1−1if Hi(t+1)≥0if Hi(t+1)<0

这里， sgn \text{sgn} sgn是符号函数，根据净输入的正负来决定神经元的输出。

如果网络达到稳定状态，即输出不再变化，那么可以认为网络已经收敛到一个存储的模式。

2.3 示例

我们的示例中网络有4个节点，存储了两个模式 ( 1 1 1 1 ) (1\ 1\ 1\ 1) (1 1 1 1)和 ( − 1 − 1 − 1 − 1 ) (-1\ -1\ -1\ -1) (−1 −1 −1 −1)。

对于不同的节点 ℓ ℓ ℓ和 j j j，权重 w ℓ , j = 1 w_{ℓ,j} =1 wℓ,j=1，对于相同的节点 j j j，权重 w j , j = 0 w_{j,j}=0 wj,j=0。

网络接收到一个损坏的输入模式 ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)。

网络随机选择一个节点进行更新。

对于节点2，计算 w 12 x 1 + w 32 x 3 + w 42 x 4 + I 2 = 1 + 1 − 1 + 1 = 2 w_{12}x_1+w_{32}x_3+w_{42}x_4+I_2=1+1-1+1=2 w12x1+w32x3+w42x4+I2=1+1−1+1=2

因此输出模式为 ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)。

对于节点4，计算 w 14 x 1 + w 24 x 2 + w 34 x 3 + I 4 = 1 + 1 + 1 − 1 = 2 w_{14}x_1+w_{24}x_2+w_{34}x_3+I_4=1+1+1-1=2 w14x1+w24x2+w34x3+I4=1+1+1−1=2

因此输出模式为 ( 1 1 1 1 ) (1\ 1\ 1\ 1) (1 1 1 1)。

没有更多的状态变化发生，网络恢复了存储的模式之一。

等距离输入模式： ( 1 1 − 1 − 1 ) (1\ 1\ -1\ -1) (1 1 −1 −1)。

对于节点2，计算 w 12 x 1 + w 32 x 3 + w 42 x 4 + I 2 = 1 − 1 − 1 + 1 = 0 w_{12}x_1+w_{32}x_3+w_{42}x_4+I_2=1-1-1+1=0 w12x1+w32x3+w42x4+I2=1−1−1+1=0

因此状态不变，输出模式为 ( 1 1 − 1 − 1 ) (1\ 1\ -1\ -1) (1 1 −1 −1)。

对于节点3，计算 w 13 x 1 + w 23 x 2 + w 43 x 4 + I 3 = 1 + 1 − 1 − 1 = 0 w_{13}x_1+w_{23}x_2+w_{43}x_4+I_3=1+1-1-1=0 w13x1+w23x2+w43x4+I3=1+1−1−1=0

但是状态从 − 1 -1 −1变为 1 1 1，输出模式为 ( 1 1 1 − 1 ) (1\ 1\ 1\ -1) (1 1 1 −1)。

对于节点4，计算 w 14 x 1 + w 24 x 2 + w 34 x 3 + I 4 = 1 + 1 − 1 − 1 = 0 w_{14}x_1+w_{24}x_2+w_{34}x_3+I_4=1+1-1-1=0 w14x1+w24x2+w34x3+I4=1+1−1−1=0

但是状态从 − 1 -1 −1变为 1 1 1，输出模式为 ( 1 1 1 1 ) (1\ 1\ 1\ 1) (1 1 1 1)。

没有更多的状态变化发生，网络恢复了存储的模式之一。

如果使用不同的节点选择顺序，网络可能会恢复不同的存储模式，例如 ( − 1 − 1 − 1 − 1 ) (-1\ -1\ -1\ -1) (−1 −1 −1 −1)。

缺失输入元素： ( 1 0 − 1 − 1 ) (1\ 0\ -1\ -1) (1 0 −1 −1)。

对于节点2，计算 w 12 x 1 + w 32 x 3 + w 42 x 4 + I 2 = 1 − 1 − 1 + 0 = − 1 w_{12}x_1+w_{32}x_3+w_{42}x_4+I_2=1-1-1+0=-1 w12x1+w32x3+w42x4+I2=1−1−1+0=−1

因此输出模式变为 ( 1 − 1 − 1 − 1 ) (1\ -1\ -1\ -1) (1 −1 −1 −1)。

对于节点1，计算 w 21 x 2 + w 31 x 3 + w 4 1 x 4 + I 1 = 0 − 1 − 1 + 1 = − 1 w_{21}x_2+w_{31}x_3+w_{4}1x_4+I_1=0-1-1+1=-1 w21x2+w31x3+w41x4+I1=0−1−1+1=−1

因此输出模式为 ( − 1 − 1 − 1 − 1 ) (-1\ -1\ -1\ -1) (−1 −1 −1 −1)。

网络同样恢复了正确的模式 ( − 1 − 1 − 1 − 1 ) (-1\ -1\ -1\ -1) (−1 −1 −1 −1)。

再比如缺失输入元素： ( 0 0 0 − 1 ) (0\ 0\ 0\ -1) (0 0 0 −1)。

网络会将其恢复成 ( − 1 − 1 − 1 − 1 ) (-1\ -1\ -1\ -1) (−1 −1 −1 −1)。

这是因为Hopfield网络中的吸引子是指网络状态的稳定点，网络在迭代过程中会收敛到这些点。在这个例子中，网络只有两个吸引子 ( 1 1 1 1 ) (1\ 1\ 1\ 1) (1 1 1 1)和 ( − 1 − 1 − 1 − 1 ) (-1\ -1\ -1\ -1) (−1 −1 −1 −1)。

当输入模式不完整或有噪声时，网络可以利用其存储的模式来补全或恢复输入模式。这是因为网络的权重矩阵是根据存储的模式计算的，使得网络能够将输入模式吸引到最近的存储模式。

当网络存储了更多的模式时，可能会出现额外的吸引子，这些吸引子不是网络设计者希望网络收敛到的稳定状态。这可能导致模式补全不正确，即网络可能收敛到一个错误的模式。

我们从前面的计算也可以得知，这里的计算其实每次结果是输入模式的四个输入和。

2.4 应用实例

Hopfield网络可以用于图像重建（Image reconstruction），即通过神经网络从部分或损坏的图像中恢复出原始图像。

这项工作是由 Ritter, Schulten, 和 Martinez 在1990年完成的。

使用的是一个20×20的离散Hopfield网络，网络被训练以识别20个输入模式。这些模式包括：

一个特定的模式（如图中左侧所示）和19个随机模式（如图中右侧所示）。

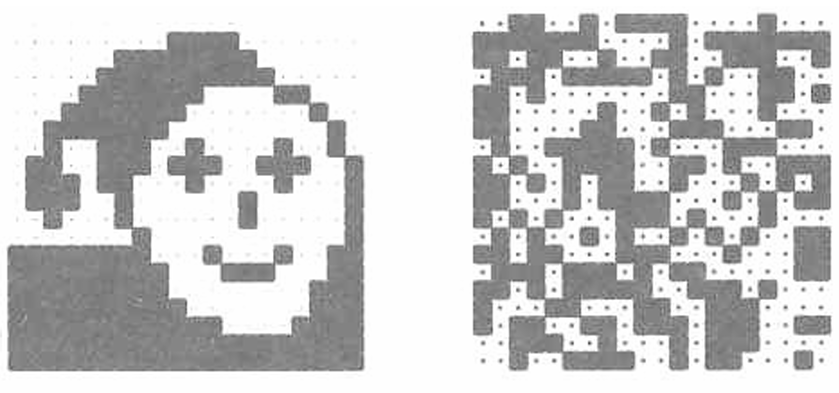
我们现在提供"面部"图像的四分之一作为初始输入。网络能够在仅仅两次迭代内完美地重建出完整的图像。

当噪声水平达到 p = 0.4 p=0.4 p=0.4时，网络无法将噪声图像恢复到原始的存储模式。这里 p p p表示噪声的强度，即图像中每个像素被随机翻转（从1变为-1或从-1变为1）的概率为40%。

相反，网络并没有恢复原始图像，而是收敛到了19个随机模式中的一个。这意味着在高噪声水平下，网络可能无法识别原始模式，而是被吸引到其他存储的模式。

2.5 以三神经元的离散Hopfield网络为例

我们再用一个最简单的例子（三神经元），把前面讲的 "稳定状态"、"吸引子"、"错误纠正" 等抽象概念可视化、具象化。

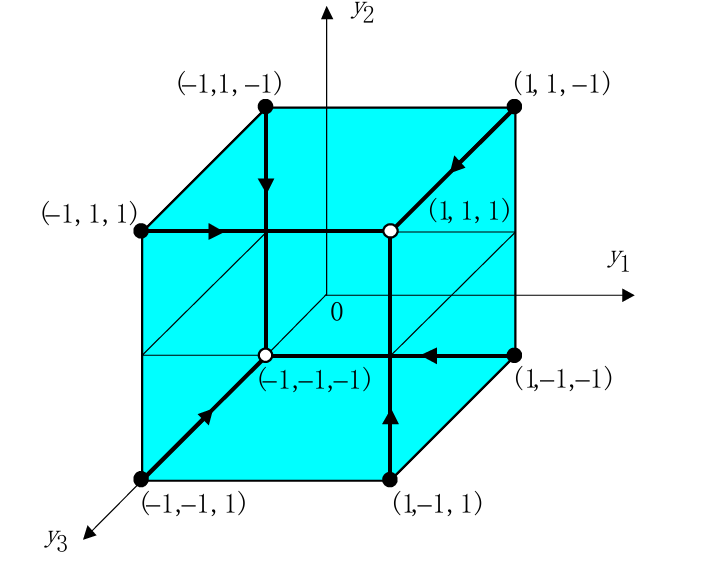
图中的三个轴分别代表三个神经元的状态，每个轴上的值可以是1或-1。

图中的每个点代表网络的一种可能状态，例如 (1,1,1) 、(−1,1,−1) 等。

因此对于三个神经元总共有 2 3 = 8 2^3=8 23=8种可能的状态组合。

稳定状态由权重矩阵 W W W、当前输入向量 X X X和阈值矩阵 q q q决定。

如果输入向量部分不正确或不完整，经过几次迭代后，初始状态将收敛到稳定状态。

假设网络需要记忆两个相反的状态，即 (1,1,1)和(−1,−1,−1) 。

状态表示为：
Y 1 = [ 1 1 1 ] Y_1 = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} Y1= 111 或 Y 1 T = [ 1 1 1 ] Y_1^T = [1 \ 1 \ 1] Y1T=[1 1 1]
Y 2 = [ − 1 − 1 − 1 ] Y_2 = \begin{bmatrix} -1 \\ -1 \\ -1 \end{bmatrix} Y2= −1−1−1 或 Y 2 T = [ − 1 − 1 − 1 ] Y_2^T = [-1 \ -1 \ -1] Y2T=[−1 −1 −1]

权重矩阵 W W W是通过以下公式计算的： W = ∑ k = 1 P x k ( x k ) T − p I W = \sum_{k=1}^{P} x^k (x^k)^T - pI W=∑k=1Pxk(xk)T−pI

其中： P P P是存储在网络中的模式数量。
x k x^k xk是第 k k k个模式向量。
I I I是单位矩阵，用于调整权重矩阵，使得对角线元素为0（即 w i i = 0 w_{ii} = 0 wii=0）。
w i j w_{ij} wij 的计算公式为：
w i j = { ∑ k = 1 p x i k x j k if i ≠ j 0 if i = j w_{ij} = \begin{cases} \sum_{k=1}^{p} x_i^k x_j^k & \text{if } i \neq j \\ 0 & \text{if } i = j \end{cases} wij={∑k=1pxikxjk0if i=jif i=j

以这里的例子 (1,1,1) 和 (−1,−1,−1) 计算权重矩阵就是首先计算每个模式向量的外积，然后求和，最后减去 p p p倍的单位矩阵。 W = [ 1 1 1 ] [ 1 1 1 ] + [ − 1 − 1 − 1 ] [ − 1 − 1 − 1 ] − 2 [ 1 0 0 0 1 0 0 0 1 ] = [ 0 2 2 2 0 2 2 2 0 ] W = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \end{bmatrix} + \begin{bmatrix} -1 \\ -1 \\ -1 \end{bmatrix} \begin{bmatrix} -1 & -1 & -1 \end{bmatrix} - 2 \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}= \begin{bmatrix} 0 & 2 & 2 \\ 2 & 0 & 2 \\ 2 & 2 & 0 \end{bmatrix} W= 111 [111]+ −1−1−1 [−1−1−1]−2 100010001 = 022202220

下一步，网络通过输入向量 X 1 X_1 X1和 X 2 X_2 X2进行测试，这些输入向量分别等于输出（或目标）向量 Y 1 Y_1 Y1和 Y 2 Y_2 Y2 。

计算如下： Y 1 = sgn ( [ 0 2 2 2 0 2 2 2 0 ] [ 1 1 0 ] ) = [ 1 1 1 ] Y_1 = \text{sgn} \left( \begin{bmatrix} 0 & 2 & 2 \\ 2 & 0 & 2 \\ 2 & 2 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} \right) = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} Y1=sgn 022202220 110 = 111

其中， sgn \text{sgn} sgn 是符号函数，如果输入值大于0，则输出1；否则输出-1。
Y 2 = sgn ( [ 0 2 2 2 0 2 2 2 0 ] [ − 1 0 0 ] ) = [ − 1 − 1 − 1 ] Y_2 = \text{sgn} \left( \begin{bmatrix} 0 & 2 & 2 \\ 2 & 0 & 2 \\ 2 & 2 & 0 \end{bmatrix} \begin{bmatrix} -1 \\ 0 \\ 0 \end{bmatrix} \right) = \begin{bmatrix} -1 \\ -1 \\ -1 \end{bmatrix} Y2=sgn 022202220 −100 = −1−1−1

最后一步是将计算得到的输出向量 Y Y Y与初始输入向量 X X X进行比较，以验证网络是否正确地恢复或识别了输入模式，我们之前记忆的输入模式是(1,1,1)和(−1,−1,−1)，因此正确识别了输入模式。

在Hopfield网络中，稳定状态是网络动态演化的吸引子。这些状态是网络在迭代过程中最终会收敛到的状态。在离散Hopfield网络中，这些状态通常是网络存储的模式。

而不稳定状态（Unstable states）不是吸引子，网络在迭代过程中不会收敛到这些状态。

以这个例子为例，我们剩余的六个状态都是不稳定状态。稳定状态(1,1,1)吸引不稳定状态(-1,1,1)，(1,-1,1)，(1,1,-1)，这些不稳定状态跟稳定状态(1,1,1)相比都有一个错误。同理，稳定状态(-1,-1,-1)吸引不稳定状态(-1,-1,1)，(-1,1,-1)，(1,-1,-1)。因此Hopfield网络可以作为错误校正网络。

2.5.1 更多示例：示例1 计算权重矩阵

现在我们有两个输入向量 x 1 = ( 1 , − 1 , − 1 , 1 ) T x^1 = (1, -1, -1, 1)^T x1=(1,−1,−1,1)T和 x 2 = ( − 1 , 0 , − 1 , 0 ) T x^2 = (-1, 0, -1, 0)^T x2=(−1,0,−1,0)T，我们现在求权重矩阵。

我们先计算它们的外积：
x 1 ( x 1 ) T = [ 1 − 1 − 1 1 ] [ 1 − 1 − 1 1 ] = [ 1 − 1 − 1 1 − 1 1 1 − 1 − 1 1 1 − 1 1 − 1 − 1 1 ] x^1 (x^1)^T = \begin{bmatrix}1 \\ -1 \\ -1 \\ 1 \end{bmatrix} \begin{bmatrix} 1 & -1 & -1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & -1 & -1 & 1 \\ -1 & 1 & 1 & -1 \\ -1 & 1 & 1 & -1 \\ 1 & -1 & -1 & 1 \end{bmatrix} x1(x1)T= 1−1−11 [1−1−11]= 1−1−11−111−1−111−11−1−11
x 2 ( x 2 ) T = [ − 1 1 − 1 1 ] [ − 1 1 − 1 1 ] = [ 1 − 1 1 − 1 − 1 1 − 1 1 1 − 1 1 − 1 − 1 1 − 1 1 ] x^2 (x^2)^T = \begin{bmatrix} -1 \\ 1 \\ -1 \\ 1 \end{bmatrix} \begin{bmatrix} -1 & 1 & -1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & -1 & 1 & -1 \\ -1 & 1 & -1 & 1 \\ 1 & -1 & 1 & -1 \\ -1 & 1 & -1 & 1 \end{bmatrix} x2(x2)T= −11−11 [−11−11]= 1−11−1−11−111−11−1−11−11

因此两者相加的结果为 [ 2 − 2 0 0 − 2 2 0 0 0 0 2 − 2 0 0 − 2 2 ] \begin{bmatrix} 2 & -2 & 0 & 0 \\ -2 & 2 & 0 & 0 \\ 0 & 0 & 2 & -2 \\ 0 & 0 & -2 & 2 \end{bmatrix} 2−200−2200002−200−22

所以 W = [ 2 − 2 0 0 − 2 2 0 0 0 0 2 − 2 0 0 − 2 2 ] − 2 [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] = [ 0 − 2 0 0 − 2 0 0 0 0 0 0 − 2 0 0 − 2 0 ] W = \begin{bmatrix} 2 & -2 & 0 & 0 \\ -2 & 2 & 0 & 0 \\ 0 & 0 & 2 & -2 \\ 0 & 0 & -2 & 2 \end{bmatrix} - 2 \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 & -2 & 0 & 0 \\ -2 & 0 & 0 & 0 \\ 0 & 0 & 0 & -2 \\ 0 & 0 & -2 & 0 \end{bmatrix} W= 2−200−2200002−200−22 −2 1000010000100001 = 0−200−2000000−200−20

2.5.2 更多示例：示例2虚假状态（spurious state）

网络有4个节点，网络被训练来存储三个模式：(1 1 -1 -1)，(1 1 1 1) 和 (-1 -1 1 1 1)。

我们权重矩阵是 W = [ 0 1 − 1 3 − 1 3 1 0 − 1 3 − 1 3 − 1 3 − 1 3 0 1 − 1 3 − 1 3 1 0 ] W = \begin{bmatrix} 0 & 1 & -\frac{1}{3} & -\frac{1}{3} \\ 1 & 0 & -\frac{1}{3} & -\frac{1}{3} \\ -\frac{1}{3} & -\frac{1}{3} & 0 & 1 \\ -\frac{1}{3} & -\frac{1}{3} & 1 & 0 \end{bmatrix} W= 01−31−3110−31−31−31−3101−31−3110

我们现在有损坏的输入模式：(-1 -1 -1 -1)

当随机选择节点4进行更新时，计算其净输入： H 4 = H 4 = ( [ − 1 3 − 1 3 1 0 ] ) [ − 1 − 1 − 1 − 1 ] T + ( − 1 ) = ( − 1 3 ⋅ − 1 − 1 3 ⋅ ( − 1 ) − 1 ⋅ 1 − 1 ⋅ 0 ) + ( − 1 ) = − 4 3 < 0 H_4 = H_4 = \left( \begin{bmatrix} -\frac{1}{3} & -\frac{1}{3} & 1 & 0 \end{bmatrix} \right) \begin{bmatrix} -1 \\ -1 \\ -1 \\ -1 \end{bmatrix}^T + (-1)= (-\frac{1}{3} \cdot -1 - \frac{1}{3} \cdot (-1) - 1 \cdot 1 - 1 \cdot 0) + (-1) = -\frac{4}{3}<0 H4=H4=([−31−3110]) −1−1−1−1 T+(−1)=(−31⋅−1−31⋅(−1)−1⋅1−1⋅0)+(−1)=−34<0

所以节点4的状态不会改变，保持为-1。

对于其他节点也是如此，网络最终稳定在损坏的输入模式 (-1 -1 -1 -1)，这不是存储的模式之一。

网络收敛到了一个没有被训练的模式，这是一个虚假状态。

这种现象表明，当网络存储的模式数量增加时，可能会出现额外的吸引子（spurious attractors），导致网络错误地完成模式补全或恢复。

再比如输入模式：(-1 -1 -1 0)

当随机选择节点4进行更新时，计算其净输入： H 4 = H 4 = ( [ − 1 3 − 1 3 1 0 ] ) [ − 1 − 1 − 1 0 ] T + 0 = ( − 1 3 ⋅ − 1 − 1 3 ⋅ ( − 1 ) − 1 ⋅ 1 − 1 ⋅ 0 ) + 0 = − 1 3 < 0 H_4 = H_4 = \left( \begin{bmatrix} -\frac{1}{3} & -\frac{1}{3} & 1 & 0 \end{bmatrix} \right) \begin{bmatrix} -1 \\ -1 \\ -1 \\ 0 \end{bmatrix}^T + 0= (-\frac{1}{3} \cdot -1 - \frac{1}{3} \cdot (-1) - 1 \cdot 1 - 1 \cdot 0) + 0 = -\frac{1}{3}<0 H4=H4=([−31−3110]) −1−1−10 T+0=(−31⋅−1−31⋅(−1)−1⋅1−1⋅0)+0=−31<0

因此输出模式更新为(-1 -1 -1 -1)。

网络最终稳定在这个状态，这是一个虚假状态，不是网络存储的模式之一。

如果节点选择顺序是1>2>3>4：

网络将收敛到状态 (-1 -1 1 1)，这是一个正确的模式。

所以Hopfield网络能够从部分或损坏的输入中恢复出完整的模式，但也可能收敛到虚假状态，特别是当网络存储的模式数量较多时。

2.6 Hopfield网络的局限性

从前面的例子中我们可以发现Hopfield网络有一些局限性。

Hopfield网络能够存储和准确回忆的模式数量是有限的。这是因为网络的容量受到其结构和权重矩阵的限制。存储过多的模式可能导致网络性能下降，因为模式之间可能会相互干扰。
在某些情况下，Hopfield网络可能会收敛到一个全新的虚假（spurious）模式，这个模式并不是网络中存储的模式之一。这种现象可能发生在输入模式与网络中存储的模式相似但不完全匹配时，网络可能会错误地收敛到一个未存储的模式。
如果一个示例模式与另一个示例模式共享许多共同的位（即"位"），那么这个示例模式可能会变得不稳定。这是因为两个模式之间的相似性可能导致网络在迭代过程中混淆这两个模式，从而影响网络的稳定性和准确性。