C++语言程序设计——【算法竞赛常用知识点】

#include <bits/stdc++.h> //万能头文件

一、字符串与数组

（一）字符串数组定义

如下代码，定义了一个能存储 10 个字符的 char 字符数组（C风格字符串），要注意最多能存储 9 个有效字符，其固定大小为 10 个字符，需包括字符串结束符 \0 ：

char a[10];    //最多能存储 9 个有效字符

同时，还定义了 C++ 标准库的 string 对象 string b，该方法是动态大小，不需要预先指定长度。

string b;

#include <iostream>
using namespace std;

int main() 
{
    char a[10];  // char 字符类型
    string b;
    cin >> a >> b;
    cout << a << endl << b;
    return 0;
}  

（二）获取长度

方法	备注
strlen()	不包括 \0
sizeof()	包括 \0

有两种获取字符串数组长度的两种方法，strlen()`从数组开头开始计算，直到遇到 '\0' 停止，其返回的是有效字符的个数，不包括 '\0'，而 sizeof()包括 '\0'。如下代码：

#include <iostream>
#include <cstring>    // 必须包含头文件
using namespace std;

int main() 
{
    char str[] = "Hello World";    // 字符数组
    cout << strlen(str) << endl;   // 不包括'\0'
    cout << sizeof(str);   // 包括11个字符 + 1个'\0'，所以12
    return 0;
}

运行结果如下：

对于C++ 中的 string 类就可以直接使用 s.size() 获取字符串长度：

string s = "今天是2025年,happy!";
cout << s.size() << endl;

另外，要注意最开始的下标固定为 0（第一个字符的位置），

最后的下标为 s.size() - 1（最后一个字符的位置）。

string s = "Sunday,happy!";
cout << s[0] << endl;           // 输出S
cout << s[s.size()-1] << endl;  // 输出!

（三）输入

cin >> 会从输入缓冲区中读取数据，但它有一个特点：遇到空白符（空格、制表符\t、换行符\n）就会停止读取，并将空白符留在缓冲区中。所以，cin 最适合读取单个、没有空格的单词或数字。

int nums[100];
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
    cin >> nums[i];
}

想读取一个词（数字或单词） → 用 cin >>

想读取一行话（带空格） → 用 cin.getline()

对于C 风格字符串的用法，可以通过cin.getline() 来读取一整行输入，包括空格，直到遇到换行符（按下回车键）为止。

cin.getline(数组名, 数组长度)   // 带空格的输入方式

此时会读取并丢弃换行符，不会把它留在缓冲区里。使用该方法需指定缓冲区大小，即最大长度。

#include <iostream>
using namespace std;

int main() 
{
    char a[10],b[10];    // 定义两个字符数组，每个最多存储9个有效字符（含结束符'\0'）
    cin.getline(a,10);   // 读取一行字符串到a，最多读取9个字符（第10个位置留给'\0'）
    cin.getline(b,10);
    cout << a << endl << b;
    return 0;
} 

如果对于 string 类，应该用以下方法：

getline(cin, 字符串变量)

例如，下面代码：

#include <iostream>
#include <string>  // 确保string类型正常使用
using namespace std;

int main() 
{
    string a;
    getline(cin, a);  // getline 传入流对象和字符串
    cout << a;
    return 0;
}

运行结果如下：

（四）遍历

对于C 风格字符串进行遍历通常使用 for 循环，结束条件是i == \0，如下：

char str[] = "hello world"; 
for (int i = 0; str[i] != '\0'; i++)  // 循环终止条件：i == \0
{  
    cout << str[i];
}

也可以通过 strlens() 作为判断条件：

char str[] = "hello world"; 
for (int i = 0; i < strlen(str); i++) 

需要导入头文件，#include < cstring > // 包含 strlen()

（五）举例

1、数字、字符串逆序

n 个元素需要的索引是 0 到 n - 1，共 n 个位置，所以循环条件用 i < n 才能准确控制输入 n 个元素数字，避免访问无效的数组位置（越界）。

int n,a[10000];
cin >> n;                   // 输入 n 个元素
for(int i = 0 ;i < n ;i++)  // 避免越界
    cin >> a[i];

定义一个数组，先输入元素的个数，通过 for 循环读取 n 个元素，之后再倒着输出 ：

#include <iostream>
using namespace std;
int n,a[10010];
int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++)   // 读取输入，也可以换成for(int i = 0; i < n; i++)
        cin >> a[i];
    for(int i = n; i >= 1; i--)   // 倒着输出，也可以换成for(int i = n-1; i >= 0; i--)
        cout << a[i] << " ";
    return 0;
}

运行结果如下：

对于一个字符串str，可以直接通过 reverse(str.begin(), str.end())，来进行字符串反转：

#include <iostream>
#include <string>
#include <algorithm>
using namespace std;

int main() 
{
    string str = "hello world";
    reverse(str.begin(), str.end());
    cout << str << endl;
    return 0;
}

或者也可以通过 for 循环逆序输出字符串，这里输入的字符串包含空格，所以需要通过 getline(cin, s) 来实现输入：

#include <iostream>
#include <string>
using namespace std;

int main() 
{
    string s;
    getline(cin, s);   // 包含空格
    
    // 倒序遍历：从最后一个字符（索引 s.length()-1）到第一个字符（索引 0）
    for (int i = s.size() - 1; i >= 0; i--) 
    {
        cout << s[i];     // 逐个输出逆序字符
    }
    cout << endl;
    return 0;
}

2、输入/输出元素

例如，a[101] 是表示数组的下标（用于访问单个元素）从 0 开始，到 100 结束（即 a[0]、a[1]、a[2]、......、a[100]），一共101个元素。下面代码中，定义了一个能存储 101 个整数的数组 s，通过循环输入 101 个整数到数组中，再通过循环将这 101 个整数逐个输出（每个数占一行）：

#include <iostream>
using namespace std;
int s[101];
int main()
{
    for(int i =0;i<101;i++)   //for(int i = 1; i <= 100; i++)
        cin>>s[i];
    for(int i =0;i<101;i++)
        cout<<s[i]<<endl;
    return 0;
}

3、不包括某个元素（排除元素）

在数组中，如果我们要输出某个不包括该元素的数组，可以通过条件语句进行判断：

for(int i = 1; i <= n; i++)
{
     if(a[i]!=s)     // 循环数组，只输出那些不等于s的元素
         cout << a[i] << " ";        
} 

在字符串中，排除某个字符，for循环条件是从 0 开始，到str.size()结束，每次 i++ 即可：

#include <iostream>
#include <string>
using namespace std;

int main() 
{
    string str = "hello world";
    char s = 'o'; // 要排除的目标字符
    for (int i = 0; i < str.size(); i++) 
    {
        if (str[i] != s) 
        {
            cout << str[i];
        }
    }
    cout << endl;
    return 0;
}

4、判断回文数

如果我们想判断一个输入的数是不是回文数，可以先进行逆转，然后再判断，其中在判断回文数组时，只需要比较前半部分和后半部分对应位置的元素，不需要重复比较：

当n=5（奇数）时，n/2=2，循环执行 2 次（比较第 0 与 4、1 与 3，中间的 2 无需比较）

当n=4（偶数）时，n/2=2，循环执行 2 次（比较第 0 与 3、1 与 2）

#include<iostream>
using namespace std;
int n,a[100];
int main()
{
    cin >> n;
    for(int i = 0; i < n; i++)
        cin >> a[i];
    for(int i = 0; i < n/2; i++)  //只需要比较前半部分和后半部分对应位置的元素
    {
        if(a[i] != a[n-1-i])//使用第i个元素和第n-1-i个元素（因为 0 开始的最后一个元素索引是n-1）
        {
            cout << "NO";
            return 0;
        }
    }
    cout << "YES";
    return 0;
}

二、数字拆分

（一）除法应用

通过取余（%10） 和 整数除法（/10） 可以获取/去掉一个整数的个位数字。

cout << 16 % 10 << endl;  //输出 6，得到个位
cout << 16 / 10 <<endl;   //输出 1，去掉个位

1、获取数字每位

对于一个数字要获取每位并输出，首先可以先统一处理正负，然后可以定义权重（即10ⁿ），从而定位该数的最高位，之后再通过 / 和 % ，从左到右逐位提取每一位：

#include <iostream>
using namespace std;

int main() 
{
    int num;
    cin >> num;

    if (num < 0) 
    {
        cout << "-";  // 提前加负号
        num = -num;   // 负数转换为正数
    }

    // 获取最高位的权重（如5→1，50→10，2234→1000）
    int weight = 1;       // 初始化权重为1（默认个位数的权重）
    int temp = num;       // 定义临时变量temp，复制num的值（避免修改原num）
    while (temp >= 10)    // 当temp是多位数（>=10）时，持续提升权重
    { 
        weight = weight * 10;   // 权重乘10，匹配最高位
        temp = temp / 10;       // 去掉temp的个位，只剩下最高位
    }

    temp = num;       // 重置temp为原正数，之前的temp已被修改为最高位数字
    while (weight > 0)    //权重小于为 0 表示所有位已输出
    {
        cout << temp / weight << " "; // 提取当前最高位
        temp = temp % weight;         // 去掉已输出的高位
        weight = weight / 10;         // 权重降位
    }
    return 0;
}

2、反转数字

通过以上方法，可以实现对数字进行反转：

cout << n % 10;  // 输出当前 n 除以 10 的余数，输出每一位
n = n / 10;      // 去掉 n 的个位数

主要就是通过取余和除法操作，逐位分解并反转数字。n % 10是获取当前数字的个位数，每次取出当前最低位的数字，而 n / 10 是去掉已经处理的个位数，使数字向右移动一位。

#include <iostream>
using namespace std;

int main() 
{
    int n;
    cin >> n;
    if (n < 0) 
    {
        cout << "-";
        n = -n;
    }
    while (n != 0) 
    {
        cout << n % 10;  // 输出当前 n 除以 10 的余数，输出每一位
        n = n / 10;      // 去掉 n 的个位数
    }
    return 0;
}

3、数字每位累加

数字每位累加依然是通过 x % 10 取个位，x / 10 去掉个位，循环直到数字为 0 结束。

#include <iostream>
using namespace std;

int main() 
{
    int n = 123, s = 0;
    int sum = 0;
    while (n != 0) 
    {
        int k = n % 10;  // 取出个位数
        sum = sum + k;   // 累加
        n = n / 10;      // 去掉个位
    }
    cout << sum;
    return 0;
}

（二）取余应用

取余通过"%"来进行运算，被除数和除数得到商，余下的就是余数。

如果负数参与取余，正常计算加负号就可以了，需要进行两个步骤（主要就看被除数）：

① 看被除数有没有负号

② 如果有，结果就有负号，否则没有

一个数字小的和一个数字大的取余，结果等于数字小的 （0 < a < b）：

小 % 大 = 小 

1、整除

（1）判断奇偶数

if(n % 2 == 0)
{
	// n是偶数
}

if(n % 2 != 0)
{
	// n是奇数
}

（2）整除（倍数）

数学中学过倍数，例如 a 是不是 b 的倍数，在于看是否存在一个整数 k ，使得 a = b × k。

其实，也可以说，看 a 是否能被 b 整除。

即 10 能被 2 整除 是等价于 10 是 2 的倍数，是因为 10 = 2 × 5，k = 5 是整数。

接下来，对 a = b × k 两边同时除以 b （因为 0 不能作为除数，所以b != 0），从而得到 a / b 的结果一定是一个整数，也就是取余等于0（a % b == 0）

所以可以得到判断条件，如果 a 能被 b 整除，则：

b != 0 && a % b == 0

#include <iostream>
using namespace std;

int main() 
{
    int a, b;
    cin >> a >> b;
    if(b != 0 && a % b == 0){
        cout << "a 能被 b 整除";
    }
    else{
        cout << "a 不能被 b 整除";
    }
    return 0;
}

（3）公倍数

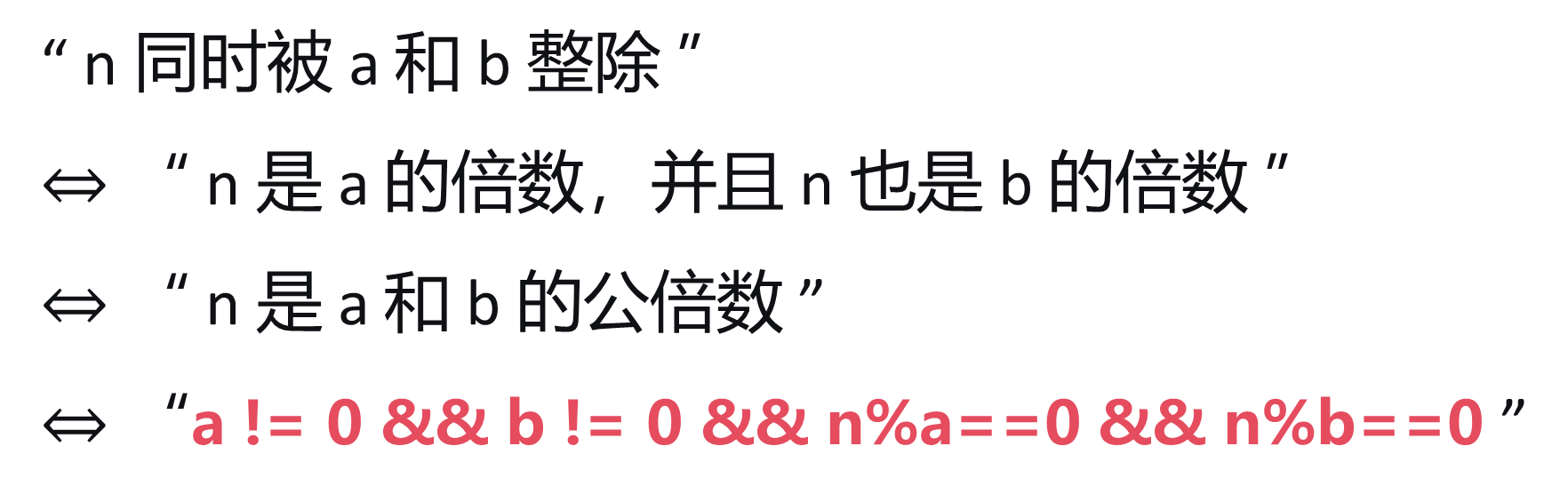
如果 n 是 a 和 b 的公倍数，则：

a != 0 && b != 0 && n % a == 0 && n % b == 0

#include <iostream>
using namespace std;

int main() 
{
    int n, a, b;
    cin >> n >> a >> b;
    if(a != 0 && b != 0 && n % a == 0 && n % b == 0){
        cout << "n是a和b的公倍数 ";
    }
    else{
        cout << "n不是a和b的公倍数 ";
    }
    return 0;
}

（4）最小公倍数

例如，我们要求两个数 a 、b 的最小公倍数，可以通过整除，不断来加上倍数进行判断，如下代码：

#include <iostream>
using namespace std;

int main() 
{
    int a, b;
    cin >> a >> b;
    if (a <= 0 || b <= 0) 
    {
        return 1;         // 程序异常结束，确保 a 和 b 均为正整数
    }
    int n = a;           // 从 a 开始
    while (b != 0 && n % b != 0)   // 直到这个数也能被 b 整除时，就是最小公倍数
    {
        n = n + a;      // 不断加上 a（保持是 a 的倍数）
    }
    cout << n;
    return 0;
}

如果是求多个数字的最小公倍数：

#include <iostream>
using namespace std;

int main() 
{
    long long num, n , lcm;
    if (!(cin >> lcm) || lcm <= 0)    // 检查第一个数是否为正整数，并假设第一个数就是当前的"最小公倍数"
    {
        return 1;
    }         
    while (cin >> num)     // 继续输入剩下的数，求 lcm 和当前数的最小公倍数
    {
        if (num <= 0) 
        {
            return 1;
        }
        n = lcm;
        while (n % num != 0) 
        {
            n = n + lcm;    // 加上当前的lcm，保证还是之前所有数的倍数
        }
        lcm = n;            // 更新lcm为新的最小公倍数
    }
    cout << lcm;
    return 0;
}

其实，最小公倍数，也可以通过 numeric 库中的 lcm()函数实现：

int result = lcm(a, b);

#include <iostream>
#include <numeric>
using namespace std;

int main() 
{
    int a, b;
    cin >> a >> b;
    if (a <= 0 || b <= 0) 
    {
        return 1;
    }
    int result = lcm(a, b);
    cout << "a和b的最小公倍数：" << result << endl;
    return 0;
}

2、数组环路遍历

利用以上取余知识点，可以实现：

当需要反复遍历一个数组，且索引到达末尾后自动回到开头，形成环路。

cout << arr[i % n] << " "; 

例如，下面代码，输入一行字符串，并输入要输出的字符个数，通过 while 循环从 i = 0 到 i < c进行循环遍历，每次输出 arr[i % n]：

i=0，0 % n = 0，输出arr[0]
i=1，1 % n = 1，输出arr[1]
i=2，2 % n = 2，输出arr[2]
...

而当 i 超过字符串长度 n 时，通过取模运算 % 循环回到数组开头继续输出：

当 i = n 时：n % n = 0，回到了数组开头，指向第一个字符
当 i = n+1 时：(n+1) % n = 1，指向第二个字符
当 i = n+2 时：(n+2) % n = 2，指向第三个字符
...

代码如下：

#include <iostream>
#include <cstring>
using namespace std;

int main()
{
    int i = 0, c , n;
    char arr[100];
    cin.getline(arr, 100);
    cin >> c;
    n = strlen(arr);
    while (i < c) 
    {
        cout << arr[i % n] << " ";     // i = n 时 n%n=0，回到开头
        i++;
    }
    return 0;
}

3、队列的插入删除

（1）插入元素：

尾指针 rear 后移。入队的代码通过取余运算实现，队尾指针加1：

Q.rear=(Q.rear+1)%MaxSize   //例如 MaxSize=5 是队列的最大长度

我们不管前面 (Q.rear+1) 为多少，它与 MaxSize（例如 MaxSize=5 是队列的最大长度）取余的结果只可能是0、1、2、3、4，也就是队尾指针 Q.rear 的每次移动加1。【入队操作只针对队尾指针，队尾指针加1取余】

//入队（插入操作）
bool EnterQueue(SqQueue &Q,int x){
	if((Q.rear+1)%MaxSize==Q.front)	//若队列为满，则报错 
		return false;
	Q.data[Q.rear]=x;	//送入入队数据元素x的值 
	Q.rear=(Q.rear+1)%MaxSize;	//队尾指针加1取模 
	return true;
}

（2）删除元素：

每次出队操作时，首先判断队列是否为空队，然后先取队列的队头元素，然后再将队头指针 Q.front 加 1 取模（通过 % 实现），出队操作针对 Q.front。

Q.front=(Q.front+1)%MaxSize;	    //例如 MaxSize=5 是队列的最大长度

队头指针加1，即 Q.front=(Q.front+1)%MaxSize。

//出队（删除操作）
bool PopQueue(SqQueue &Q,int x) {
	if(Q.front==Q.rear)	//若队列为空，则报错 
		return false;
	x=Q.data[Q.front];	//取出队头数据元素x的值 
	Q.front=(Q.front+1)%MaxSize;	//队头指针加1取模 
	return true;
}

我们不管前面 (Q.front+1) 为多少，它与 MaxSize（例如MaxSize=5 是队列的最大长度）取余的结果只可能是0、1、2、3、4，也就是队头指针 Q.front 的每次移动加1。【出队操作只针对队头指针，队头指针加1取余】

4、数组元素移位

以下移位操作以右移为例，例如需要右移 k 位：

dx =(i + k) % n   // 计算目标位置索引

数组长度为 n ，数组索引为 i 的元素，向后移动 k 位，如果超出数组末尾，则通过取余 %n 回到数组开头。

同样，左移也是通过取余，不过需要加上数组长度，因为如果超出数组开头，则+n后取余 %n 回到数组末尾（避免负数索引）。

dy = (i - k + n) % n	   // 计算目标位置索引

右移 k 位的代码如下：

#include <iostream>
using namespace std;

int main() 
{
    int nums[100],temp[100];   // temp 数组用于移位后存储移位的元素
    int n,k;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> nums[i];
    }
    cout << "输入右移位数：";
    cin >> k;
    k = k % n;  // k是移位次数，处理 k 大于 n 的情况，例如：n=5, k=7 => k=2 (7%5=2)
    for (int i = 0; i < n; i++) 
    {
        int dx = (i + k) % n;  // 计算目标位置索引
        temp[dx] = nums[i];    // 将原数组元素放到临时数组的目标位置
    }   
    for (int i = 0; i < n; i++) 
    {
        nums[i] = temp[i];  // 将临时数组复制回原数组
    }
    for (int i = 0; i < n; i++) 
    {
        cout << nums[i] << " ";   // 输出移位后的数组
    }
    return 0;
}

三、栈和队列

栈相关知识点可查看之前的文章：https://wink-augenstern.blog.csdn.net/article/details/124575864

队列相关知识点可查看之前的文章：https://wink-augenstern.blog.csdn.net/article/details/125166210

（一）栈

stack 可存储 C++ 中任意基础数据类型（如整型、浮点型、字符型、布尔型等），声明格式在 <> 中填写类型名即可。

#include <stack>
stack<char> int_st;        // 整型栈
stack<char> char_st;       // 字符栈
stack<string> str_st;      // 字符串栈

#include <iostream>
#include <stack>
using namespace std;

int main() 
{
    int n, number;
    stack<int> st;   //声明一个整数栈
    cin >> n;

    for (int i = 0; i < n; i++) 
    {
        cin >> number;
        st.push(number);    // 将输入元素push 压入栈【入栈】
    }

    cout << "栈大小：" << st.size() << endl;    // 获取栈的元素个数

    cout << "栈顶元素：" << st.top() << endl;   // 访问栈顶元素
    st.pop();     // 弹出栈顶元素【出栈】
    st.pop();
    cout << "弹出后栈顶元素：" << st.top() << endl;
    cout << "弹出后栈大小：" << st.size() << endl;

    cout << "遍历栈元素：";
    while (!st.empty())    // 遍历栈，empty是判断栈是否为空
    {
        cout << st.top() << " ";
        st.pop();
    }
    return 0;
}

举例

给定一个只包含 '('、')'、'{'、'}'、'['、']' 的字符串 s，判断该字符串是否为有效的括号字符串。有效括号字符串需满足：

①左括号必须用相同类型的右括号闭合；

②左括号必须以正确的顺序闭合。

输入格式：

一行输入一个字符串 s（长度 1 ≤ s.length ≤ 10^4）

输出格式：

如果字符串是有效的括号字符串，输出 true，否则输出 false

#include <iostream>
#include <stack>
#include <string>
using namespace std;

int main() 
{
    string s;
    cin >> s;
    stack<char> st;     // 字符类型栈

    for (int i = 0; i < s.size(); i++) 
    {
        char c = s[i];
        if (c == ')' || c == '}' || c == ']') 
        {
            if (st.empty()) // 栈为空 → 无对应左括号
            {
                cout << "false" << endl;
                return 0;
            }
            char top = st.top();     // 取出栈顶左括号，判断是否匹配
            st.pop();
            if ((c == ')' && top != '(') ||(c == '}' && top != '{') ||(c == ']' && top != '['))
            {
                cout << "false" << endl;
                return 0;
            }
        } 
        else 
        {
            st.push(c);            // 左括号 → 压入栈
        }
    }

    // 遍历结束后，判断栈是否为空
    if (st.empty()) {
        cout << "true" << endl;
    } else {
        cout << "false" << endl;
    }
    return 0;
}

（二）队列

queue 可存储 C++ 中任意基础数据类型（如整型、浮点型、字符型、布尔型等），声明格式也是在 <> 中填写类型名即可。

#include <iostream>
#include <queue>  // 队列头文件（替换栈的stack头文件）
using namespace std;

int main() 
{
    int n, number;
    queue<int> q;   // 声明一个整数队列（替换栈的stack<int> st）
    cin >> n;

    for (int i = 0; i < n; i++) 
    {
        cin >> number;
        q.push(number);    // 将输入元素push 压入队尾【入队】（栈是压入栈顶，队列是压入队尾）
    }

    cout << "队列大小：" << q.size() << endl;    // 获取队列的元素个数（与栈的size用法一致）

    cout << "队首元素：" << q.front() << endl;   // 访问队首元素（替换栈的top()，队列用front()取队首）
    q.pop();     // 弹出队首元素【出队】（栈是弹出栈顶，队列是弹出队首）
    q.pop();
    cout << "弹出后队首元素：" << q.front() << endl;  // 出队后访问新队首
    cout << "弹出后队列大小：" << q.size() << endl;

    cout << "遍历队列元素：";
    while (!q.empty())    // 遍历队列，empty判断队列是否为空（与栈的empty用法一致）
    {
        cout << q.front() << " ";  // 队列遍历输出队首元素
        q.pop();                   // 弹出已输出的队首元素（遍历后队列清空）
    }
    return 0;
}

举例

约瑟夫环问题是一个经典的数学和编程问题：有 n 个人围成一个圆圈，从第 1 个人开始按顺时针方向报数，报到第 k个数的人出列；接着从出列的下一个人开始继续报数，如此循环，直到圈中只剩下最后一个人，输出这个人的初始编号。

输入格式：

一行输入两个整数 n 和 k（1 ≤ n ≤ 1000，1 ≤ k ≤ 100），分别表示人数和报数阈值。

输出格式：

输出最后剩下的人的初始编号（编号从 1 到 n）。

#include <iostream>
#include <queue>
using namespace std;

int main() 
{
    int n, k;
    cin >> n >> k;
    queue<int> q;

    int count = 0;         // 计数
    for (int i = 1; i <= n; i++)   // 编号入队（1~n）
    {
        q.push(i);
    }

    while (q.size() > 1)     // 循环报数淘汰，直到只剩1人
    {
        count++;
        int front = q.front();  // 取出队首（当前报数的人）
        q.pop();

        if (count != k) 
        {
            q.push(front);     // 报数未到k，重新入队（循环到队尾）
        } 
        else 
        {
            count = 0;  // 报数到k，淘汰（不重新入队），并且重置计数器，下一轮重新报数
        }
    }
    cout << q.front();   // 队列中剩余的最后1人即为答案
    return 0;
}

四、递归

例如，我们要计算从 1 一直加到 100 的和，除了用 for 循环也可以使用递归来完成，例如计算 1 + 2 + 3 + 4 + 5 的和：

sum(5)

= 5 + sum(4)

= 5 + (4 + sum(3))

= 5 + (4 + (3 + sum(2)))

= 5 + (4 + (3 + (2 + sum(1))))

= 5 + (4 + (3 + (2 + 1))) // sum(1)返回1

= 5 + (4 + (3 + 3))

= 5 + (4 + 6)

= 5 + 10

= 15

从 1 一直加到 100 的和，通过递归实现，如下：

#include <iostream>
using namespace std;

int sum(int n) 
{
    if (n == 1) {
        return 1;
    }
    else {
        return n + sum(n - 1);    // sum(n) = n + sum(n-1)
    }
}

int main() 
{
    int result = sum(100);
    cout << "1 + 2 + ... + 100 = " << result;
    return 0;
}

五、动态规划

动态规划相关文章可见之前文章：https://wink-augenstern.blog.csdn.net/article/details/133905694

一、斐波那契数列

一个楼梯，每次只能跨越 1 级或 2 级，一共有 n 级台阶，有多少走法。

最优子结构：当前台阶的走法数 = 前一台阶走法数 + 前二台阶走法数。
重叠子问题：计算第 n 级台阶时，需要用到第 n-1 和 n-2 级的结果，需要重复使用。
方程：dp[n] = dp[n-1] + dp[n-2]

#include <iostream>
using namespace std;

int main() 
{
    int n;
    cin >> n;
    if (n <= 2)     // 如果台阶数n是1或2，直接输出结果
    {
        cout << n;
        return 0;
    }
    long long a = 1 , b = 2 , c;  // a代表前前一级台阶的走法数,b代表前一级台阶的走法数,c代表当前台阶的走法数
    for (int i = 3; i <= n; i++) 
    {
        c = a + b;   // 当前台阶的走法 = 前前一级走法 + 前一级走法
        a = b;    // 更新a：下一次循环要算i+1级，此时的前前一级就是现在的前一级（b）
        b = c;    // 更新b：下一次循环要算i+1级，此时的前一级就是现在的当前级（c）
    }
    cout << b;
    return 0;
}

二、走格子

16×16 格子中，从起点 (0,0)开始，到终点 (15,15)结束，每次只能右 / 下走，求按照该方式的路径数目。

首先，因为只能向右 / 向下走，可以先将第一行和第一列初始化为 1，再从第二行第二列开始，每个格子的路径数等于上方格子与左方格子路径数之和，从而最终 num [15][15] 即为从起点到终点的总路径数。

假设到达( i , j)，则：
最优子结构：只能从上面或左边过来，

当前格子(i,j)的路径数 = 上方格子(i-1,j)的路径数 + 左方格子的(i,j-1)路径数
重叠子问题：在计算(i , j)时，需要计算(i-1, j)和(i, j-1)，计算(i-1, j)又需要(i-2, j)和(i-1, j-1)，需重复使用。
方程：dp[i][j] = dp[i-1][j] + dp[i][j-1]

#include <iostream>
using namespace std;

int main() 
{
    const int N = 16;
    int num[N][N] = {1};        // 起点本身算1条路径，其余元素默认0
    for (int i = 0; i < N; i++) // 外层循环，遍历每一行（从0到15）
    {
        num[0][i] = 1;  // 第一行只能一直向右走，全为1
        num[i][0] = 1;  // 第一列只能一直向下走，全为1
        if(i >= 1)      // 处理非第一行的格子
        {
            for (int j = 1; j < N; j++) // 内层循环：遍历当前行的每一列（j从1到15）
            {
                num[i][j] = num[i-1][j] + num[i][j-1];   // 到(x,y)的路径数 = 从上方来的路径数 + 从左方来的路径数
            }
        }
    }
    cout << num[15][15];
    return 0;
}