本节继续讲解李群李代数推导方式的相对位姿雅可比,上节讲到了对两时刻同时左扰动的方式,但是这样推导过于复杂,这一节讲解如何利用对两时刻单独左扰动的方式推导,依然使用相同的图来说明
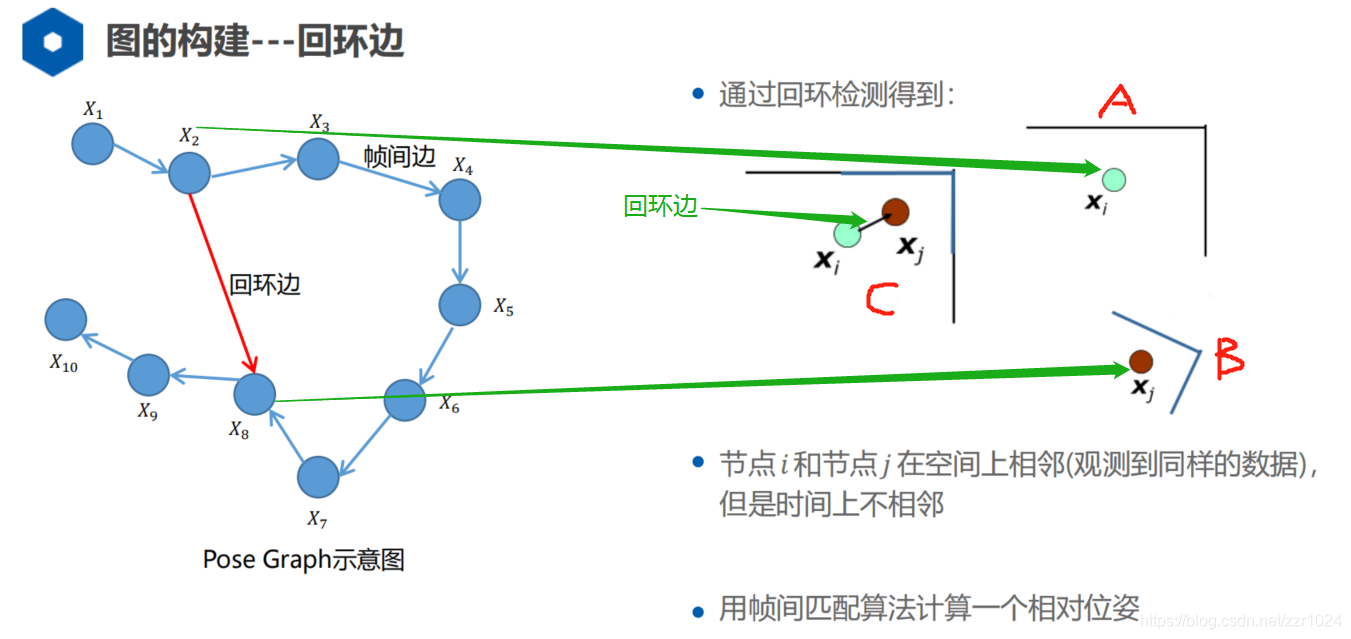
同上节一样,先来点基础知识
一. 基础知识
1. 伴随矩阵性质
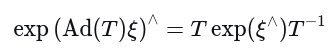
对两边同时施展逆变换可得
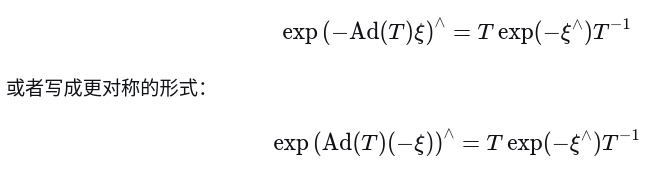
2. 左右扰动
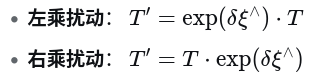
二. 问题描述
位姿图残差项为:
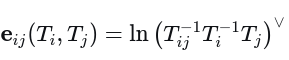
目的利用BCH公式,将施加扰动后的残差项变为类似如下形式
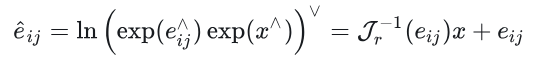
三. 雅可比推导
1. 先对i时刻求导
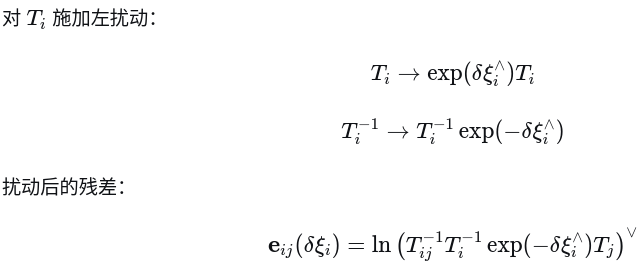

实际是在上式左侧乘了一个单位元, 等式即可成立
代入到扰动后的残差
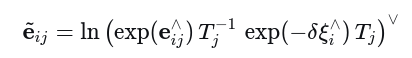

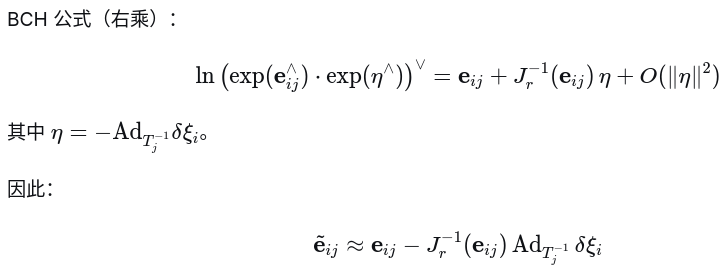
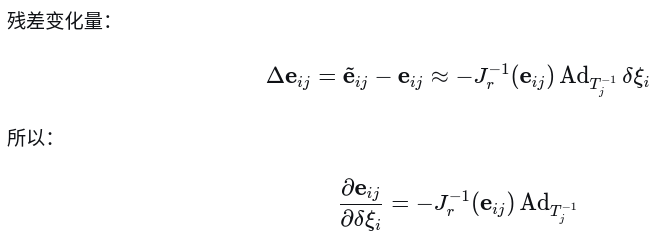
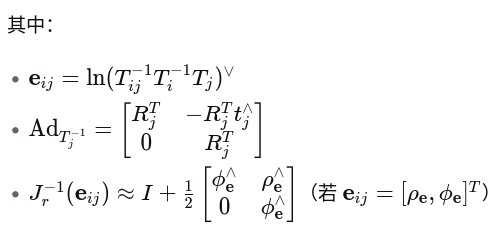
这样推导了i时刻的雅可比,与上节推导一模一样,但更直观更简洁
2. 再对j时刻求导
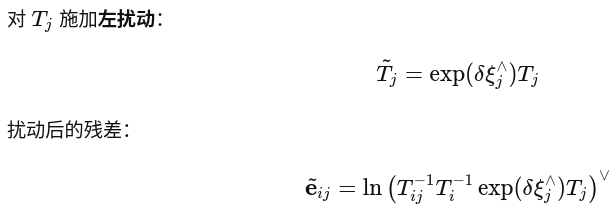

代入到扰动后的残差
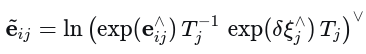
直接利用伴随性质即可
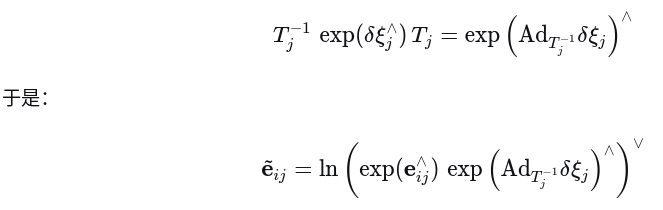
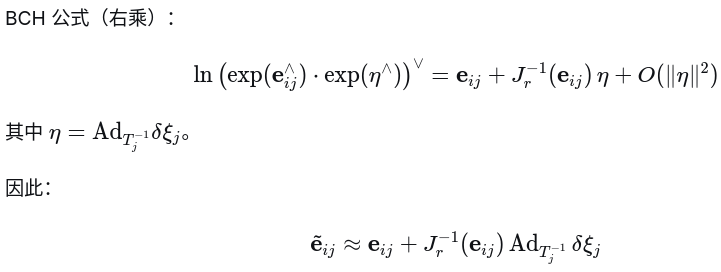
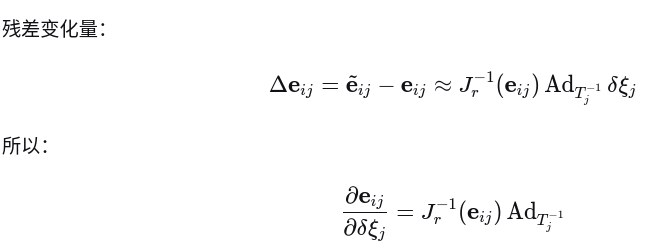
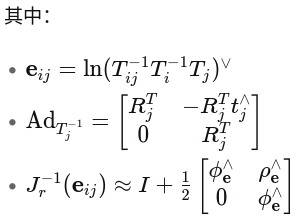
3. 将两个结果放一起对比
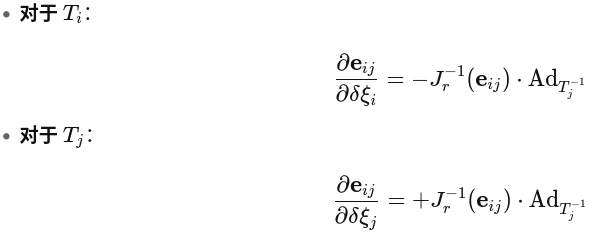


这个对称而优美的结果显示了李群理论在推导中的强大威力
四. 总结
本节以伴随跟BCH公式为基础,直接推导了左乘扰动后的雅可比矩阵,并且最终结论与上节完全一致,相对上节的推导,单个求扰动后的雅可比更加简洁,更加容易理解,不过实现路径虽有不同,最终结论确是一致的,因此可以得出一个结论,再求解雅可比矩阵的时候,选择合适的扰动方式,往往能事半功倍。
附录
对上述几何解释中的符号相反做一个说明


为啥残差保持不变,符合相反的雅可比就是正确的呢?




简单的总结为: 只有扰动相同时,残差会保持不变,雅可比为0,这也就意味着相对位姿无法消除零空间


