可持久化线段树和标记永久化

little~钰2025-12-06 16:15

单点修改

单点修改 单点查询

P3919 【模板】可持久化线段树 1（可持久化数组） - 洛谷

java 复制代码 
// 单点修改的可持久化线段树模版题1，java版
// 给定一个长度为n的数组arr，下标1~n，原始数组认为是0号版本
// 一共有m条操作，每条操作是如下两种类型中的一种
// v 1 x y : 基于v号版本的数组，把x位置的值设置成y，生成新版本的数组
// v 2 x   : 基于v号版本的数组，打印x位置的值，生成新版本的数组和v版本一致
// 每条操作后得到的新版本数组，版本编号为操作的计数
// 1 <= n, m <= 10^6
// 测试链接 : https://www.luogu.com.cn/problem/P3919
// 提交以下的code，提交时请把类名改成"Main"，可以通过所有测试用例

import java.io.InputStream;
import java.io.OutputStream;
import java.io.IOException;

public class Code01_PointPersistent1 {

	public static int MAXN = 1000001;

	public static int MAXT = MAXN * 23;

	public static int n, m;

	// 原始数组
	public static int[] arr = new int[MAXN];

	// 可持久化线段树需要
	// root[i] : i号版本线段树的头节点编号
	public static int[] root = new int[MAXN];

	public static int[] left = new int[MAXT];

	public static int[] right = new int[MAXT];

	// value[i] : 节点i的值信息，只有叶节点有这个信息
	public static int[] value = new int[MAXT];

	// 可持久化线段树的节点空间计数
	public static int cnt = 0;

	// 建树，返回头节点编号
	public static int build(int l, int r) {
		int rt = ++cnt;
		if (l == r) {
			value[rt] = arr[l];
		} else {
			int mid = (l + r) >> 1;
			left[rt] = build(l, mid);
			right[rt] = build(mid + 1, r);
		}
		return rt;
	}

	// 线段树范围l~r，信息在i号节点里
	// 在l~r范围上，jobi位置的值，设置成jobv
	// 生成的新节点编号返回
	public static int update(int jobi, int jobv, int l, int r, int i) {
		int rt = ++cnt;
		left[rt] = left[i];
		right[rt] = right[i];
		value[rt] = value[i];
		if (l == r) {
			value[rt] = jobv;
		} else {
			int mid = (l + r) >> 1;
			if (jobi <= mid) {
				left[rt] = update(jobi, jobv, l, mid, left[rt]);
			} else {
				right[rt] = update(jobi, jobv, mid + 1, r, right[rt]);
			}
		}
		return rt;
	}

	// 线段树范围l~r，信息在i号节点里
	// 返回l~r范围上jobi位置的值
	public static int query(int jobi, int l, int r, int i) {
		if (l == r) {
			return value[i];
		}
		int mid = (l + r) >> 1;
		if (jobi <= mid) {
			return query(jobi, l, mid, left[i]);
		} else {
			return query(jobi, mid + 1, r, right[i]);
		}
	}

	public static void main(String[] args) {
		FastIO io = new FastIO(System.in, System.out);
		n = io.nextInt();
		m = io.nextInt();
		for (int i = 1; i <= n; i++) {
			arr[i] = io.nextInt();
		}
		root[0] = build(1, n);
		for (int i = 1, version, op, x, y; i <= m; i++) {
			version = io.nextInt();
			op = io.nextInt();
			x = io.nextInt();
			if (op == 1) {
				y = io.nextInt();
				root[i] = update(x, y, 1, n, root[version]);
			} else {
				root[i] = root[version];
				io.writelnInt(query(x, 1, n, root[i]));
			}
		}
		io.flush();
	}

单点修改 范围查询

P3834 【模板】可持久化线段树 2 - 洛谷

java 复制代码 
// 单点修改的可持久化线段树模版题2，java版
// 给定一个长度为n的数组arr，下标1~n，一共有m条查询
// 每条查询 l r k : 打印arr[l..r]中第k小的数字
// 1 <= n、m <= 2 * 10^5
// 0 <= arr[i] <= 10^9
// 测试链接 : https://www.luogu.com.cn/problem/P3834
// 提交以下的code，提交时请把类名改成"Main"，可以通过所有测试用例

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;

public class Code02_PointPersistent1 {

	public static int MAXN = 200001;

	public static int MAXT = MAXN * 22;

	public static int n, m, s;

	// 原始数组
	public static int[] arr = new int[MAXN];

	// 收集权值排序并且去重做离散化
	public static int[] sorted = new int[MAXN];

	// 可持久化线段树需要
	// root[i] : 插入arr[i]之后形成新版本的线段树，记录头节点编号
	// 0号版本的线段树代表一个数字也没有时，每种名次的数字出现的次数
	// i号版本的线段树代表arr[1..i]范围内，每种名次的数字出现的次数
	public static int[] root = new int[MAXN];

	public static int[] left = new int[MAXT];

	public static int[] right = new int[MAXT];

	// 排名范围内收集了多少个数字
	public static int[] size = new int[MAXT];

	public static int cnt;

	// 返回num在所有值中排名多少
	public static int kth(int num) {
		int left = 1, right = s, mid, ans = 0;
		while (left <= right) {
			mid = (left + right) / 2;
			if (sorted[mid] <= num) {
				ans = mid;
				left = mid + 1;
			} else {
				right = mid - 1;
			}
		}
		return ans;
	}

	// 排名范围l~r，建立线段树，返回头节点编号
	public static int build(int l, int r) {
		int rt = ++cnt;
		size[rt] = 0;
		if (l < r) {
			int mid = (l + r) / 2;
			left[rt] = build(l, mid);
			right[rt] = build(mid + 1, r);
		}
		return rt;
	}

	// 排名范围l~r，信息在i号节点，增加一个排名为jobi的数字
	// 返回新的头节点编号
	public static int insert(int jobi, int l, int r, int i) {
		int rt = ++cnt;
		left[rt] = left[i];
		right[rt] = right[i];
		size[rt] = size[i] + 1;
		if (l < r) {
			int mid = (l + r) / 2;
			if (jobi <= mid) {
				left[rt] = insert(jobi, l, mid, left[rt]);
			} else {
				right[rt] = insert(jobi, mid + 1, r, right[rt]);
			}
		}
		return rt;
	}

	// 排名范围l~r，老版本信息在u号节点，新版本信息在v号节点
	// 返回，第jobk小的数字，排名多少
	public static int query(int jobk, int l, int r, int u, int v) {
		if (l == r) {
			return l;
		}
		int lsize = size[left[v]] - size[left[u]];
		int mid = (l + r) / 2;
		if (lsize >= jobk) {
			return query(jobk, l, mid, left[u], left[v]);
		} else {
			return query(jobk - lsize, mid + 1, r, right[u], right[v]);
		}
	}

	// 权值做离散化并且去重 + 生成各版本的线段树
	public static void prepare() {
		cnt = 0;
		for (int i = 1; i <= n; i++) {
			sorted[i] = arr[i];
		}
		Arrays.sort(sorted, 1, n + 1);
		s = 1;
		for (int i = 2; i <= n; i++) {
			if (sorted[s] != sorted[i]) {
				sorted[++s] = sorted[i];
			}
		}
		root[0] = build(1, s);
		for (int i = 1, x; i <= n; i++) {
			x = kth(arr[i]);
			root[i] = insert(x, 1, s, root[i - 1]);
		}
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StreamTokenizer in = new StreamTokenizer(br);
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		in.nextToken();
		n = (int) in.nval;
		in.nextToken();
		m = (int) in.nval;
		for (int i = 1; i <= n; i++) {
			in.nextToken();
			arr[i] = (int) in.nval;
		}
		prepare();
		for (int i = 1, l, r, k, rank; i <= m; i++) {
			in.nextToken();
			l = (int) in.nval;
			in.nextToken();
			r = (int) in.nval;
			in.nextToken();
			k = (int) in.nval;
			rank = query(k, 1, s, root[l - 1], root[r]);
			out.println(sorted[rank]);
		}
		out.flush();
		out.close();
		br.close();
	}

}

范围修改

经典实现

SP11470 TTM - To the moon - 洛谷

java 复制代码 
// 范围修改的可持久化线段树，经典的方式，java版
// 给定一个长度为n的数组arr，下标1~n，时间戳t=0，arr认为是0版本的数组
// 一共有m条操作，每条操作为如下四种类型中的一种
// C x y z : 当前时间戳t版本的数组，[x..y]范围每个数字增加z，得到t+1版本数组，并且t++
// Q x y   : 当前时间戳t版本的数组，打印[x..y]范围累加和
// H x y z : z版本的数组，打印[x..y]范围的累加和
// B x     : 当前时间戳t设置成x
// 1 <= n、m <= 10^5
// -10^9 <= arr[i] <= +10^9
// 测试链接 : https://www.luogu.com.cn/problem/SP11470
// 测试链接 : https://www.spoj.com/problems/TTM
// 提交以下的code，提交时请把类名改成"Main"
// java实现的逻辑一定是正确的，但是通过不了
// 因为这道题根据C++的运行时间，制定通过标准，根本没考虑java的用户
// 想通过用C++实现，本节课Code03_RangePersistentClassic2文件就是C++的实现
// 两个版本的逻辑完全一样，C++版本可以通过所有测试

import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStreamWriter;

public class Code03_RangePersistentClassic1 {

	public static int MAXN = 100001;

	public static int MAXT = MAXN * 70;

	public static int n, m, t = 0;

	public static int[] arr = new int[MAXN];

	public static int[] root = new int[MAXN];

	public static int[] left = new int[MAXT];

	public static int[] right = new int[MAXT];

	// 累加和信息
	public static long[] sum = new long[MAXT];

	// 懒更新信息，范围增加的懒更新
	public static long[] add = new long[MAXT];

	public static int cnt = 0;

	public static int clone(int i) {
		int rt = ++cnt;
		left[rt] = left[i];
		right[rt] = right[i];
		sum[rt] = sum[i];
		add[rt] = add[i];
		return rt;
	}

	public static void up(int i) {
		sum[i] = sum[left[i]] + sum[right[i]];
	}

	public static void lazy(int i, long v, int n) {
		sum[i] += v * n;
		add[i] += v;
	}

	public static void down(int i, int ln, int rn) {
		if (add[i] != 0) {
			left[i] = clone(left[i]);
			right[i] = clone(right[i]);
			lazy(left[i], add[i], ln);
			lazy(right[i], add[i], rn);
			add[i] = 0;
		}
	}

	public static int build(int l, int r) {
		int rt = ++cnt;
		add[rt] = 0;
		if (l == r) {
			sum[rt] = arr[l];
		} else {
			int mid = (l + r) / 2;
			left[rt] = build(l, mid);
			right[rt] = build(mid + 1, r);
			up(rt);
		}
		return rt;
	}

	public static int add(int jobl, int jobr, long jobv, int l, int r, int i) {
		int rt = clone(i);
		if (jobl <= l && r <= jobr) {
			lazy(rt, jobv, r - l + 1);
		} else {
			int mid = (l + r) / 2;
			down(rt, mid - l + 1, r - mid);
			if (jobl <= mid) {
				left[rt] = add(jobl, jobr, jobv, l, mid, left[rt]);
			}
			if (jobr > mid) {
				right[rt] = add(jobl, jobr, jobv, mid + 1, r, right[rt]);
			}
			up(rt);
		}
		return rt;
	}

	public static long query(int jobl, int jobr, int l, int r, int i) {
		if (jobl <= l && r <= jobr) {
			return sum[i];
		}
		int mid = (l + r) / 2;
		down(i, mid - l + 1, r - mid);
		long ans = 0;
		if (jobl <= mid) {
			ans += query(jobl, jobr, l, mid, left[i]);
		}
		if (jobr > mid) {
			ans += query(jobl, jobr, mid + 1, r, right[i]);
		}
		return ans;
	}

	public static void main(String[] args) throws IOException {
		FastReader in = new FastReader();
		BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
		n = in.nextInt();
		m = in.nextInt();
		for (int i = 1; i <= n; i++) {
			arr[i] = in.nextInt();
		}
		root[0] = build(1, n);
		String op;
		for (int i = 1, x, y, z; i <= m; i++) {
			op = in.next();
			if (op.equals("C")) {
				x = in.nextInt();
				y = in.nextInt();
				z = in.nextInt();
				root[t + 1] = add(x, y, z, 1, n, root[t]);
				t++;
			} else if (op.equals("Q")) {
				x = in.nextInt();
				y = in.nextInt();
				out.write(query(x, y, 1, n, root[t]) + "\n");
			} else if (op.equals("H")) {
				x = in.nextInt();
				y = in.nextInt();
				z = in.nextInt();
				out.write(query(x, y, 1, n, root[z]) + "\n");
			} else {
				x = in.nextInt();
				t = x;
			}
		}
		out.flush();
		out.close();
	}

标记永久化实现普通线段树

对于重置操作：如果把一个大范围重置为x，那么子范围的重置任务必须下发清除，大范围和其子范围的重置任务是不独立的，不能标记永久化

对于最大/小值：如果3-6范围增加6，但1-10范围的最大值是不能像累加和一样直接更新出来的

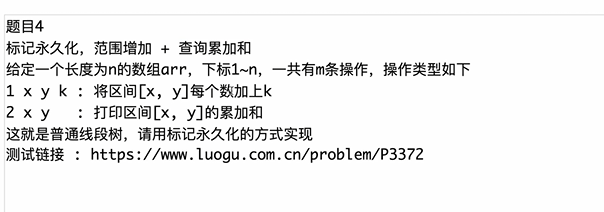
以下面这颗树为例

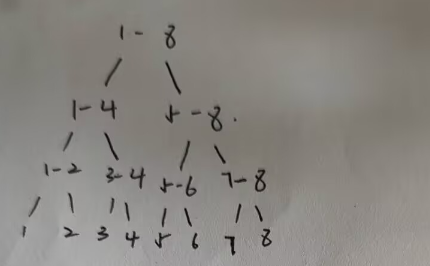
1.在1-8加5，那么1-8sum更新为40，addtag为5（addtag不再像懒信息一样下发）

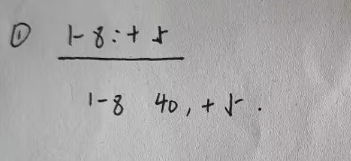
2.3-4减2：那么1-8sum就减4变为36，addtag不变；1-4sum变为-4，1-4没有被3-4全包，addtag还是为0；3-4sum变为-4，addtag为-2

3.最后，如果求3-4的累加和，就把从1-8开始到3-4的路径上所有addtag相加为5，5*(4-3+1) (3-4范围上的数字个数)+(-4)(3-4范围上的sum)就是累加和

P3372 【模板】线段树 1 - 洛谷

java 复制代码 
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;

public class Code04_TagPermanentization1 {

	public static int MAXN = 100001;

	public static long[] arr = new long[MAXN];

	// 不是真实累加和，而是之前的任务中
	// 不考虑被上方范围截住的任务，只考虑来到当前范围 或者 往下走的任务
	// 累加和变成了什么
	public static long[] sum = new long[MAXN << 2];

	// 不再是懒更新信息，变成标记信息
	public static long[] addTag = new long[MAXN << 2];

	public static void build(int l, int r, int i) {
		if (l == r) {
			sum[i] = arr[l];
		} else {
			int mid = (l + r) / 2;
			build(l, mid, i << 1);
			build(mid + 1, r, i << 1 | 1);
			sum[i] = sum[i << 1] + sum[i << 1 | 1];
		}
		addTag[i] = 0;
	}

	public static void add(int jobl, int jobr, long jobv, int l, int r, int i) {
		int a = Math.max(jobl, l), b = Math.min(jobr, r);
		sum[i] += jobv * (b - a + 1);
		if (jobl <= l && r <= jobr) {
			addTag[i] += jobv;
		} else {
			int mid = (l + r) / 2;
			if (jobl <= mid) {
				add(jobl, jobr, jobv, l, mid, i << 1);
			}
			if (jobr > mid) {
				add(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);
			}
		}
	}

	public static long query(int jobl, int jobr, long addHistory, int l, int r, int i) {
		if (jobl <= l && r <= jobr) {
			return sum[i] + addHistory * (r - l + 1);
		}
		int mid = (l + r) >> 1;
		long ans = 0;
		if (jobl <= mid) {
			ans += query(jobl, jobr, addHistory + addTag[i], l, mid, i << 1);
		}
		if (jobr > mid) {
			ans += query(jobl, jobr, addHistory + addTag[i], mid + 1, r, i << 1 | 1);
		}
		return ans;
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StreamTokenizer in = new StreamTokenizer(br);
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		in.nextToken();
		int n = (int) in.nval;
		in.nextToken();
		int m = (int) in.nval;
		for (int i = 1; i <= n; i++) {
			in.nextToken();
			arr[i] = (long) in.nval;
		}
		build(1, n, 1);
		int op, jobl, jobr;
		long jobv;
		for (int i = 1; i <= m; i++) {
			in.nextToken();
			op = (int) in.nval;
			if (op == 1) {
				in.nextToken();
				jobl = (int) in.nval;
				in.nextToken();
				jobr = (int) in.nval;
				in.nextToken();
				jobv = (long) in.nval;
				add(jobl, jobr, jobv, 1, n, 1);
			} else {
				in.nextToken();
				jobl = (int) in.nval;
				in.nextToken();
				jobr = (int) in.nval;
				out.println(query(jobl, jobr, 0, 1, n, 1));
			}
		}
		out.flush();
		out.close();
		br.close();
	}

}

标记永久化实现可持久化线段树

Problem - 4348

java 复制代码 
// 范围修改的可持久化线段树，标记永久化减少空间占用，java版
// 给定一个长度为n的数组arr，下标1~n，时间戳t=0，arr认为是0版本的数组
// 一共有m条查询，每条查询为如下四种类型中的一种
// C x y z : 当前时间戳t版本的数组，[x..y]范围每个数字增加z，得到t+1版本数组，并且t++
// Q x y   : 当前时间戳t版本的数组，打印[x..y]范围累加和
// H x y z : z版本的数组，打印[x..y]范围的累加和
// B x     : 当前时间戳t设置成x
// 1 <= n、m <= 10^5
// -10^9 <= arr[i] <= +10^9
// 测试链接 : https://acm.hdu.edu.cn/showproblem.php?pid=4348
// 提交以下的code，提交时请把类名改成"Main"
// java实现的逻辑一定是正确的，但是通过不了
// 因为这道题根据C++的运行空间，制定通过标准，根本没考虑java的用户
// 想通过用C++实现，本节课Code05_RangePersistentLessSpace2文件就是C++的实现
// 两个版本的逻辑完全一样，C++版本可以通过所有测试

import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStreamWriter;

public class Code05_RangePersistentLessSpace1 {

	public static int MAXN = 100001;

	public static int MAXT = MAXN * 25;

	public static int n, m, t = 0;

	public static int[] arr = new int[MAXN];

	public static int[] root = new int[MAXN];

	public static int[] left = new int[MAXT];

	public static int[] right = new int[MAXT];

	// 不是真实累加和，而是之前的任务中
	// 不考虑被上方范围截住的任务，只考虑来到当前范围 或者 往下走的任务
	// 累加和变成了什么
	public static long[] sum = new long[MAXT];

	// 不再是懒更新信息，变成标记信息
	public static long[] addTag = new long[MAXT];

	public static int cnt = 0;

	public static int build(int l, int r) {
		int rt = ++cnt;
		addTag[rt] = 0;
		if (l == r) {
			sum[rt] = arr[l];
		} else {
			int mid = (l + r) / 2;
			left[rt] = build(l, mid);
			right[rt] = build(mid + 1, r);
			sum[rt] = sum[left[rt]] + sum[right[rt]];
		}
		return rt;
	}

	public static int add(int jobl, int jobr, long jobv, int l, int r, int i) {
		int rt = ++cnt, a = Math.max(jobl, l), b = Math.min(jobr, r);
		left[rt] = left[i];
		right[rt] = right[i];
		sum[rt] = sum[i] + jobv * (b - a + 1);
		addTag[rt] = addTag[i];
		if (jobl <= l && r <= jobr) {
			addTag[rt] += jobv;
		} else {
			int mid = (l + r) / 2;
			if (jobl <= mid) {
				left[rt] = add(jobl, jobr, jobv, l, mid, left[rt]);
			}
			if (jobr > mid) {
				right[rt] = add(jobl, jobr, jobv, mid + 1, r, right[rt]);
			}
		}
		return rt;
	}

	public static long query(int jobl, int jobr, long addHistory, int l, int r, int i) {
		if (jobl <= l && r <= jobr) {
			return sum[i] + addHistory * (r - l + 1);
		}
		int mid = (l + r) / 2;
		long ans = 0;
		if (jobl <= mid) {
			ans += query(jobl, jobr, addHistory + addTag[i], l, mid, left[i]);
		}
		if (jobr > mid) {
			ans += query(jobl, jobr, addHistory + addTag[i], mid + 1, r, right[i]);
		}
		return ans;
	}

	public static void main(String[] args) throws IOException {
		FastReader in = new FastReader();
		BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
		n = in.nextInt();
		m = in.nextInt();
		for (int i = 1; i <= n; i++) {
			arr[i] = in.nextInt();
		}
		root[0] = build(1, n);
		String op;
		for (int i = 1, x, y, z; i <= m; i++) {
			op = in.next();
			if (op.equals("C")) {
				x = in.nextInt();
				y = in.nextInt();
				z = in.nextInt();
				root[t + 1] = add(x, y, z, 1, n, root[t]);
				t++;
			} else if (op.equals("Q")) {
				x = in.nextInt();
				y = in.nextInt();
				out.write(query(x, y, 0, 1, n, root[t]) + "\n");
			} else if (op.equals("H")) {
				x = in.nextInt();
				y = in.nextInt();
				z = in.nextInt();
				out.write(query(x, y, 0, 1, n, root[z]) + "\n");
			} else {
				x = in.nextInt();
				t = x;
			}
		}
		out.flush();
		out.close();
	}
相关推荐
獭.獭.1 小时前
C++ -- 二叉搜索树
数据结构·c++·算法·二叉搜索树
TOYOAUTOMATON1 小时前
自动化工业夹爪
大数据·人工智能·算法·目标检测·机器人
im_AMBER1 小时前
Leetcode 67 长度为 K 子数组中的最大和 | 可获得的最大点数
数据结构·笔记·学习·算法·leetcode
feifeigo1233 小时前
MATLAB实现两组点云ICP配准
开发语言·算法·matlab
fengfuyao9853 小时前
粒子群算法（PSO）求解标准VRP问题的MATLAB实现
开发语言·算法·matlab
Ayanami_Reii3 小时前
进阶数据结构应用-SPOJ 3267 D-query
数据结构·算法·线段树·主席树·持久化线段树
guygg883 小时前
基于全变差的压缩感知视频图像重构算法
算法·重构·音视频
VT LI4 小时前
SDF在实时图形渲染中的核心原理与架构创新
算法·sdf·有号距离场
想七想八不如114084 小时前
408操作系统 PV专题
开发语言·算法
热门推荐
01GitHub 镜像站点02React CVE-2025-55182漏洞排查与修复指南03【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05UV安装并设置国内源06BongoCat - 跨平台键盘猫动画工具07智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践08本地部署阿里最新开源的Z-Image09Linux下V2Ray安装配置指南10论文阅读 - 深度学习端到端解决库存管理问题 - 有限时间范围内的多周期补货问题（Management Science）