《算法闯关指南：动态规划算法--斐波拉契数列模型》--04.解码方法

🔥草莓熊Lotso： 个人主页
❄️个人专栏: 《C++知识分享》《Linux 入门到实践：零基础也能懂》
✨生活是默默的坚持，毅力是永久的享受！

🎬 博主简介：

文章目录

前言：
04.解码方法
结语：

前言：

聚焦算法题实战，系统讲解三大核心板块：优选算法：剖析动态规划、二分法等高效策略，学会寻找"最优解"。递归与回溯：掌握问题分解与状态回退，攻克组合、排列等难题。贪心算法：理解"局部最优"到"全局最优"的思路，解决区间调度等问题内容以题带点，讲解思路与代码实现，帮助大家快速提升代码能力。

04.解码方法

题目链接：

91. 解码方法 - 力扣（LeetCode）

题目描述：

题目示例：

解法（动态规划）：

算法思路：

类似于斐波拉契数列~
1. 状态表示 ：

根据以往经验，对于大多数线性 dp，我们经验上都是【以某个位置结束或者开始】做文章，这里我们继续尝试【以 i 位置结尾】结合【题目要求】来定义状态表示。
dp[i] 表示：字符串中【0，i】区间上，一共有多少种编码方法。
2. 状态转移方程 ：

定义好状态表示，我们就可以分析 i 位置的 dp 的值，如何由【前面】或者【后面】的信息推到出来。

关于 i 位置的编码状况，我们可以分为以下两种情况：

让 i 位置上的数单独解码成一个字母；
让 i 位置上的数与 i-1 位置上的结合，解码成一个字母。

下面我们就上面的两种解码情况，继续分析：

让 i 位置上的数单独解码成一个字母，就存在【解码成功】和【解码失败】两种情况：
- 解码成功：当 i 位置上的数在【1，9】之间的时候，说明 i 位置上的数是可以单独解码的，那么此时【0，i】区间上的解码方式应该等于【0，i-1】区间上的解码方法。因为【0，i-1】区间上的所有解码结果，后面填上一个 i 位置解码后的字母就可以了。此时 dp[i] = dp[i-1];
- 解码失败：当 i 位置上的数是 0 的时候，说明 i 位置上的数是不能单独解码的，那么此时【0，i】区间上不存在解码方法。因为 i 位置如果单独参与解码，但是解码失败了，那么前面做的努力就全部白费了。此时 dp[i] = 0。
让 i 位置上的数与 i-1 位置上的数结合在一起，解码成一个字母，也存在【解码成功】和【解码失败】两种情况：
- 解码成功：当结合的数在【10，26】之间的时候，说明【i-1，i】两个位置是可以解码成功的，那么此时【0，i】区间上的解码方法应该等于【0，i-2】区间上的解码方式，原因同上。此时 dp[i] = dp[i-2]。
- 解码失败：当结合的数在【0，9】和【27，99】之间的时候，说明两个位置结合后解码失败(这里一定要注意 00 01 02 03 04......这些情况)，那么此时【0，i】区间上的解码方法就不存在了，原因依旧同上。此时 dp[i] = 0。

综上所述 ：dp[i] 最终的结果应该是上面四种情况下，解码成功的两种的累加和(因为我们关心的是解码方式，既然解码失败，就不用加入到最终结果中去)，因此可以得到状态转移方程(dp[i] 默认初始化为 0)：

当 s[i] 上的数在【1，9】区间上时：dp[i] += dp[i-1] ；
当 s[i] 与 s[i-1] 上的数结合后，在【10，26】之间的时候：dp[i] += dp[i-2]；

如果上述两个判断都不成立，说明没有解码方法，dp[i] 就是默认值 0。

3. 初始化 ：
方法一(直接初始化) ：

由于可能要用到 i-1 以及 i-2 位置上的 dp 值，因此要先初始化【前两个位置】。

初始化 dp[0]：

当 s[0] == '0' 时，没有编码方法，结果 dp[0] = 0；
当 s[0] != '0' 时，能编码成功，dp[0] = 1

初始化 dp[1]：

当 s[i] 在【1，9】之间时，能单独编码，此时 dp[1] += dp[0] （原因同上，dp[1] 默认为 0）
当 s[0] 与 s[1] 结合后的数在【10，26】之间时，说明在前两个字符中，又有一种编码方式，此时 dp[1] += 1。

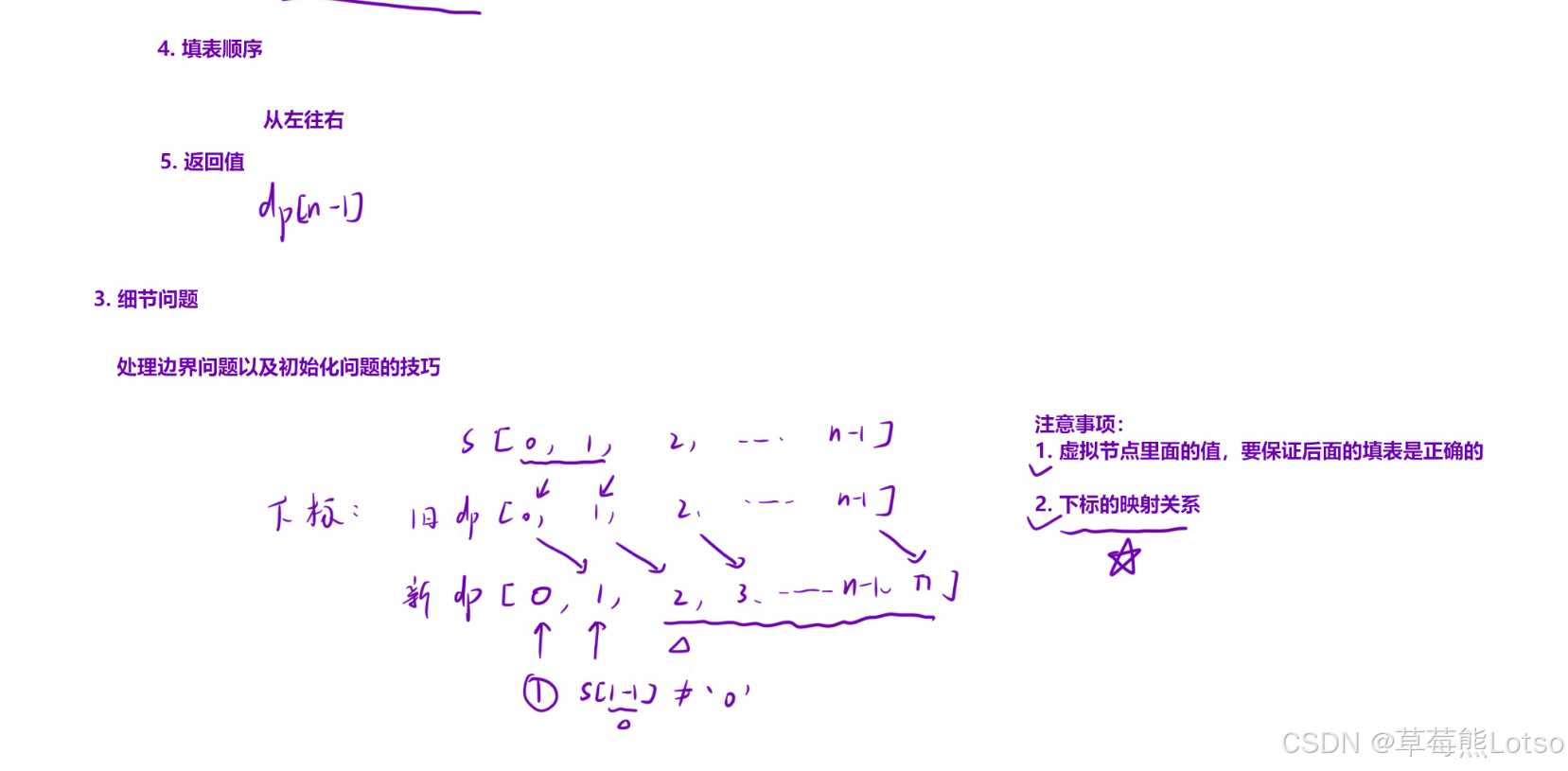
方法二（添加辅助位置初始化）：

可以在前面加上一个虚拟结点(辅助结点)，帮助我们初始化。使用这种技巧要注意两个点：

辅助结点里面的值要保证后续填表是正确的；
下标的映射关系

4. 填表顺序 ：

毫无疑问是【从左往右】

5. 返回值 ：

应该返回 dp[n-1] 的值，表示在【0，n-1】区间上的编码方法。如果是按第二种方式初始化，就返回 dp[n]。

C++算法代码：

cpp 复制代码

class Solution {
public:
    int numDecodings(string s) {
        // 1. 创建 dp 表
        // 2. 初始化
        // 3. 填表
        // 4. 返回

        int n=s.size();
        vector<int>dp(n);
        dp[0]=s[0]!='0';
        if(n==1) return dp[0];
        if(s[0]!='0'&&s[1]!='0') dp[1]+=1;
        int t=(s[0]-'0')*10+s[1]-'0';
        if(t>=10&&t<=26) dp[1]+=1;

        for(int i=2;i<n;i++)
        {
            if(s[i]!='0') dp[i]+=dp[i-1];
            int t=(s[i-1]-'0')*10+s[i]-'0';
            if(t>=10&&t<=26) dp[i]+=dp[i-2];
        }
        return dp[n-1];
    }
};

使用添加辅助1结点发方式初始化：

cpp 复制代码

class Solution {
public:
    int numDecodings(string s) {
        // 初始化优化

        int n = s.size();
        vector<int> dp(n+1);//多开一个
        dp[0] = 1;//虚拟节点初始化，这里是1，保证后面填表是正确的
        dp[1] = s[1-1] != '0';//注意下标的映射关系

        for(int i = 2;i <= n;i++)//这里变成了<=n
        {
            if(s[i - 1] != '0') dp[i] += dp[i - 1];
            int t = (s[i - 2] - '0')*10 + s[i - 1] - '0';
            if(t >= 10 && t <= 26) dp[i] += dp[i - 2];
        }
        return dp[n];//返回值变成了dp[n]
    }
};

算法总结&&笔记展示：

笔记字有点丑，大家见谅：

结语：

html 复制代码

🍓 我是草莓熊 Lotso！若这篇技术干货帮你打通了学习中的卡点：
👀 【关注】跟我一起深耕技术领域，从基础到进阶，见证每一次成长
❤️ 【点赞】让优质内容被更多人看见，让知识传递更有力量
⭐ 【收藏】把核心知识点、实战技巧存好，需要时直接查、随时用
💬 【评论】分享你的经验或疑问（比如曾踩过的技术坑？），一起交流避坑
🗳️ 【投票】用你的选择助力社区内容方向，告诉大家哪个技术点最该重点拆解
技术之路难免有困惑，但同行的人会让前进更有方向～愿我们都能在自己专注的领域里，一步步靠近心中的技术目标！

结语：本文以动态规划为核心，详细解析LeetCode 91题"解码方法"。通过状态表示（dp[i]记录0~i区间的解码方式数）和分类讨论（单独解码/联合解码的成功与失败情况），推导出状态转移方程。提供两种初始化方案（直接初始化/辅助节点优化），并给出C++代码实现。笔记以手写形式总结关键点，强调分情况处理边界条件（如'0'的特殊性）和下标映射关系。算法时间复杂度O(n)，空间复杂度O(n)，适用于数字字符串解码问题。

✨把这些内容吃透超牛的！放松下吧✨ ʕ˘ᴥ˘ʔ づきらど