leetcode 3578

3578: 统计极差最大为K的分割方式数

思路：单调队列+动态规划

单调队列是一种特殊的队列数据结构，它维护队列中的元素具有单调性（单调递增或单调递减）。它主要用于解决++滑动窗口类问题++ ，可以在O(n)时间内解决一些看似需要O(n²)时间的问题，适合处理需要维护区间最值的问题。

单调队列的核心思想是：

• 维护一个双端队列（deque）

• 队列中的元素保持单调性

• 及时移除不再有用的元素

• 保证队列头部始终是当前窗口的最值

0 <= k <= 10^9

一般定义 fi+1 表示++前缀++ nums0 到 numsi 在题目约束下，分割出的最少（最多）子数组个数，本题是定义成分割方案数。

动态规划：我们设 dpi+1 表示以 i 为结尾的前缀子数组 nums0⋯i 满足题目要求的分割方案数，++初始化 dp0=1，此时前缀为空也看作为一种合法的分割。++ 可分割成一个或多个 **非空** 的连续子段枚举最后一个子数组的左端点 j，那么问题变成前缀 nums0 到 numsj−1 在题目约束下的分割方案数，即 fj。当子数组++右端点 i 固定时++ ，由于子数组越长，最大值越大，最小值越小，最大最小的差值越可能大于 k。所以符合要求的++左端点 j++ 一定在一个连续区间 L,i 中。累加 fj 得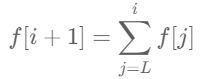递归，分割方案数求和

答案为 fn。

deque<int> min_q, max_q;

两个完全独立的双端队列，同步地 维护一个滑动窗口的最小值 和最大值（即"单调队列"最经典的用法）

while(!min_q.empty() && x<=nums[min_q.back()]){ 
    min_q.pop_back();
}
min_q.push_back(i);
while(!max_q.empty() && x>=nums[max_q.back()]){
    max_q.pop_back();
}
max_q.push_back(i);

• min_q：把"大于等于 x 的"从尾端踢掉 → 队列里严格单调递增（头小尾大）。

• max_q：把"小于等于 x 的"从尾端踢掉 → 队列里严格单调递减（头大尾小）。

所以
min_q 是递增队列 ，队头存当前窗口最小值 ；
max_q 是递减队列 ，队头存当前窗口最大值。

class Solution {
public:
    int countPartitions(vector<int>& nums, int k) {
        constexpr int MOD=1'000'000'007;
        int n=nums.size();
        deque<int> min_q,max_q; //获得窗口中的最大、最小值
        vector<int> f(n+1); //动态规划,f[0]~f[n]递归
        f[0]=1;
        long long sum_f=0; // 窗口中的 f[i] 之和
        int left=0; 

        for(int i=0;i<n;i++){
            int x=nums[i];
            sum_f+=f[i]; //滑动窗口-入

            while(!min_q.empty() && x<=nums[min_q.back()]){ 
                min_q.pop_back();
            }
            min_q.push_back(i);
            while(!max_q.empty() && x>=nums[max_q.back()]){
                max_q.pop_back();
            }
            max_q.push_back(i);

            while(nums[max_q.front()]-nums[min_q.front()]>k){ //最大值与最小值作差超过k
                sum_f-=f[left]; //滑动窗口-出，类前缀和
                left++;
                if(min_q.front()<left){
                    min_q.pop_front();
                }
                if(max_q.front()<left){
                    max_q.pop_front();
                }
            }
            f[i+1]=sum_f%MOD;
        }

        return f[n];
    }
};