三角函数的和角公式
sin ( α + β ) = sin α cos β + cos α sin β \sin(\alpha + \beta) = \sin\alpha \cos\beta + \cos\alpha \sin\beta sin(α+β)=sinαcosβ+cosαsinβ正弦和公式
cos ( α + β ) = cos α cos β − sin α sin β \cos(\alpha + \beta) = \cos\alpha \cos\beta - \sin\alpha \sin\beta cos(α+β)=cosαcosβ−sinαsinβ余弦和公式
距离公式及余弦定理证明余弦差公式
O是原心,A和B是以O为圆心,1为半径的点。
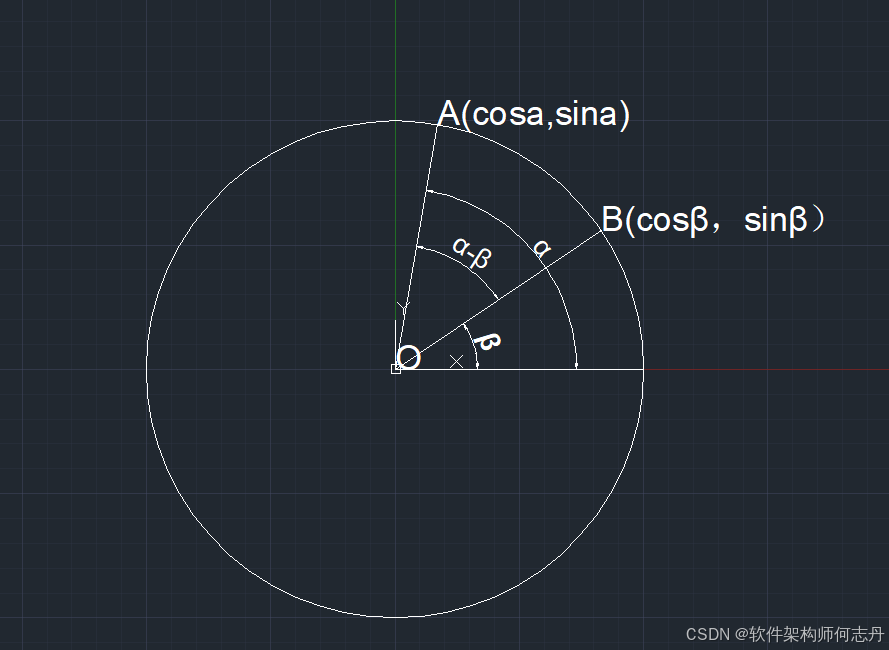
∣ A B ∣ 2 = ( cos α − cos β ) 2 + ( sin α − sin β ) 2 |AB|^2=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2 ∣AB∣2=(cosα−cosβ)2+(sinα−sinβ)2
= cos 2 α − 2 c o s α cos β + cos 2 β + sin 2 α − 2 sin α sin β + sin 2 β =\cos^2\alpha -2cos\alpha\cos\beta+\cos^2\beta+\sin^2\alpha-2\sin\alpha\sin\beta+\sin^2\beta =cos2α−2cosαcosβ+cos2β+sin2α−2sinαsinβ+sin2β
2 − 2 cos α cos β − 2 sin α sin β 2-2\cos\alpha\cos\beta-2\sin\alpha\sin\beta 2−2cosαcosβ−2sinαsinβ 因为 s i n 2 α + c o s 2 α = = 1 sin^2\alpha+cos^2\alpha==1 sin2α+cos2α==1
根据余弦定理:
∣ A B ∣ 2 = ∣ O A ∣ 2 + ∣ O B ∣ 2 − 2 ∣ O A ∣ ∣ O A ∣ cos ( α − β ) |AB|^2=|OA|^2+|OB|^2-2|OA||OA|\cos(\alpha-\beta) ∣AB∣2=∣OA∣2+∣OB∣2−2∣OA∣∣OA∣cos(α−β)
= 1 + 1 − 2 cos ( α − β ) =1+1-2\cos(\alpha-\beta) =1+1−2cos(α−β)
联立两式得 cos ( α − β ) = c o s α cos β + sin α sin β \cos(\alpha-\beta)=cos\alpha\cos\beta+\sin\alpha\sin\beta cos(α−β)=cosαcosβ+sinαsinβ 余弦差公式
余弦和公式
cos ( α − ( − β ) ) = c o s α cos ( − β ) + sin α sin ( − β ) = cos α cos β − sin α sin β \cos(\alpha-(-\beta))=cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta cos(α−(−β))=cosαcos(−β)+sinαsin(−β)=cosαcosβ−sinαsinβ余弦和公式
正弦和公式
sin ( α + β ) = cos ( ( π ÷ 2 − α ) − β ) = sin α cos β + cos α sin α \sin(\alpha+\beta)=\cos((\pi\div 2-\alpha)-\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\alpha sin(α+β)=cos((π÷2−α)−β)=sinαcosβ+cosαsinα
二维矢量逆时针旋转
v ⃗ = ( r cos α , r sin α ) \vec v=(r\cos\alpha,r\sin\alpha) v =(rcosα,rsinα),旋转 β \beta β后,变成:
x'= r cos ( α + β ) = r cos α cos β − r sin α sin β r\cos(\alpha+\beta) =r\cos\alpha\cos\beta-r\sin\alpha\sin\beta rcos(α+β)=rcosαcosβ−rsinαsinβ 余弦和定理
y'= r sin ( α + β ) = r sin α cos β + r cos α sin β r\sin(\alpha+\beta)=r\sin\alpha\cos\beta+r\cos\alpha\sin\beta rsin(α+β)=rsinαcosβ+rcosαsinβ 正弦定理
令x= r cos α r\cos\alpha rcosα,y=r sin α \sin\alpha sinα
x'= x cos β − y sin β x\cos\beta-y\sin\beta xcosβ−ysinβ
y'= y c o s β + x s i n β ycos\beta+xsin\beta ycosβ+xsinβ
x ′ y ′ \] = \[ cos θ − sin θ sin θ cos θ \] \[ x y \] \\begin{bmatrix} x' \\\\ y' \\end{bmatrix} =\\begin{bmatrix} \\cos\\theta \& -\\sin\\theta \\\\ \\sin\\theta \& \\cos\\theta \\end{bmatrix} \\begin{bmatrix} x \\\\ y \\end{bmatrix} \[x′y′\]=\[cosθsinθ−sinθcosθ\]\[xy
旋转 9 0 ∘ 90^\circ 90∘ (-y,x)
旋转 − 9 0 ∘ -90^\circ −90∘(y,-x)
三维旋转
绕x轴旋转
R x ( θ ) = [ 1 0 0 0 cos θ − sin θ 0 sin θ cos θ ] \mathbf{R}_x(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix} Rx(θ)= 1000cosθsinθ0−sinθcosθ
x ′ y ′ z ′ \] = R x ( θ ) \[ x y z \] = \[ x y cos θ − z sin θ y sin θ + z cos θ \] \\begin{bmatrix} x' \\\\ y' \\\\ z' \\end{bmatrix} = \\mathbf{R}_x(\\theta) \\begin{bmatrix} x \\\\ y \\\\ z \\end{bmatrix} =\\begin{bmatrix} x \\\\ y \\cos\\theta - z \\sin\\theta \\\\ y \\sin\\theta + z \\cos\\theta \\end{bmatrix} x′y′z′ =Rx(θ) xyz = xycosθ−zsinθysinθ+zcosθ
绕y轴旋转
R y ( θ ) = \[ cos θ 0 sin θ 0 1 0 − sin θ 0 cos θ \] \\mathbf{R}_y(\\theta) = \\begin{bmatrix} \\cos\\theta \& 0 \& \\sin\\theta \\\\ 0 \& 1 \& 0 \\\\ -\\sin\\theta \& 0 \& \\cos\\theta \\end{bmatrix} Ry(θ)= cosθ0−sinθ010sinθ0cosθ
\[ x ′ y ′ z ′ \] = R y ( θ ) \[ x y z \] = \[ x cos θ + z sin θ y − x sin θ + z cos θ \] \\begin{bmatrix} x' \\\\ y' \\\\ z' \\end{bmatrix} =\\mathbf{R}_y(\\theta)\\begin{bmatrix}x \\\\ y \\\\ z\\end{bmatrix} =\\begin{bmatrix} x \\cos\\theta + z \\sin\\theta \\\\ y \\\\ -x \\sin\\theta + z \\cos\\theta \\end{bmatrix} x′y′z′ =Ry(θ) xyz = xcosθ+zsinθy−xsinθ+zcosθ
## 绕z轴旋转
R z ( θ ) = \[ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 \] \\mathbf{R}_z(\\theta) = \\begin{bmatrix} \\cos\\theta \& -\\sin\\theta \& 0 \\\\ \\sin\\theta \& \\cos\\theta \& 0 \\\\ 0 \& 0 \& 1 \\end{bmatrix} Rz(θ)= cosθsinθ0−sinθcosθ0001
\[ x ′ y ′ z ′ \] = R z ( θ ) \[ x y z \] = \[ x cos θ − y sin θ x sin θ + y cos θ z \] \\begin{bmatrix} x' \\\\ y' \\\\ z' \\end{bmatrix} =\\mathbf{R}_z(\\theta) \\begin{bmatrix} x \\\\ y \\\\ z \\end{bmatrix} =\\begin{bmatrix} x \\cos\\theta - y \\sin\\theta \\\\ x \\sin\\theta + y \\cos\\theta \\\\ z \\end{bmatrix} x′y′z′ =Rz(θ) xyz = xcosθ−ysinθxsinθ+ycosθz
矩阵形式的罗德里格斯公式
R = \[ u x 2 ( 1 − c ) + c u x u y ( 1 − c ) − u z s u x u z ( 1 − c ) + u y s u x u y ( 1 − c ) + u z s u y 2 ( 1 − c ) + c u y u z ( 1 − c ) − u x s u x u z ( 1 − c ) − u y s u y u z ( 1 − c ) + u x s u z 2 ( 1 − c ) + c \] \\boxed{ \\mathbf{R} = \\begin{bmatrix} u_x\^2(1-c)+c \& u_x u_y(1-c)-u_z s \& u_x u_z(1-c)+u_y s \\\\ u_x u_y(1-c)+u_z s \& u_y\^2(1-c)+c \& u_y u_z(1-c)-u_x s \\\\ u_x u_z(1-c)-u_y s \& u_y u_z(1-c)+u_x s \& u_z\^2(1-c)+c \\end{bmatrix} } R= ux2(1−c)+cuxuy(1−c)+uzsuxuz(1−c)−uysuxuy(1−c)−uzsuy2(1−c)+cuyuz(1−c)+uxsuxuz(1−c)+uysuyuz(1−c)−uxsuz2(1−c)+c
其中
c=cosθ,s=sinθ。

## 扩展阅读
| 我想对大家说的话 |
|----------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 工作中遇到的问题,可以按类别查阅鄙人的算法文章,请点击《[算法与数据汇总](https://blog.csdn.net/he_zhidan/article/details/137131684)》。 |
| 学习算法:按章节学习《[喜缺全书算法册](https://download.csdn.net/download/he_zhidan/88348653)》,大量的题目和测试用例,[打包下载](https://blog.csdn.net/he_zhidan/article/details/140733677)。重视操作 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 员工说:技术至上,老板不信;投资人的代表说:技术至上,老板会信。 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
| 失败+反思=成功 成功+反思=成功 |
### 视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。