文章目录
摘要
本周学习了DDIM和DIT,对DDIM的采样过程进行了推导和DiT对扩散模型所做的工作。
Abstract
This week, I studied DDIM and DiT, deriving the sampling process of DDIM and examining the work DiT has done on diffusion models.
1 DDIM
DDPM在生成过程中,需要完整的去噪一千次才可以从噪声图片得到生成图片,生成的时间会很久,于是Jiaming Song, Chenlin Meng, Stefano Ermon等人就提出了DDIM。
1.1 构造
DDPM需要逐步去噪是由于马尔科夫性质,于是就构造一个不需要马尔科夫的采样来进行生成,就可以解决逐步去噪的问题,DDPM的采样过程
p ( x t ∣ x t − 1 ) x t = α t x t − 1 + β t ε t , β t = 1 − α t x t = α t ( α t − 1 x t − 2 + β t − 1 ε t − 1 ) + β t ε t x t = α t α t − 1 . . . α 1 x 0 + 1 − α t α t − 1 . . . α 1 ε , ε ∼ N ( 0 , I ) x t = α t ‾ x 0 + 1 − α ‾ t ε p ( x t ∣ x 0 ) ∼ N ( α t ‾ x 0 , 1 − α ‾ t ) \begin{aligned}p(x_t|x_{t-1}) \\ x_t&=\sqrt{\alpha_t}x_{t-1}+\sqrt{\beta_t}\varepsilon_t,\beta_t=1-\alpha_t \\ x_t&=\sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{\beta_{t-1}}\varepsilon_{t-1})+\sqrt{\beta_t}\varepsilon_t \\ x_t&=\sqrt{\alpha_t\alpha_{t-1}...\alpha_1}x_0+\sqrt{1-\alpha_t\alpha_{t-1}...\alpha_1}\varepsilon,\varepsilon \sim N(0,I) \\ x_t &=\sqrt{\overline{\alpha_t}}x_0+\sqrt{1-\overline \alpha_t}\varepsilon \\p(x_t|x_0) &\sim N(\sqrt{\overline{\alpha_t}}x_0,1-\overline \alpha_t) \end{aligned} p(xt∣xt−1)xtxtxtxtp(xt∣x0)=αt xt−1+βt εt,βt=1−αt=αt (αt−1 xt−2+βt−1 εt−1)+βt εt=αtαt−1...α1 x0+1−αtαt−1...α1 ε,ε∼N(0,I)=αt x0+1−αt ε∼N(αt x0,1−αt)
p ( x t − 1 ∣ x t ) = p ( x t ∣ x t − 1 ) p ( x t − 1 ) p ( x t ) , p ( x t ∣ x t − 1 ) ∼ N ( α t x t − 1 , β t ) p(x_{t-1}|x_t)=\frac{p(x_t|x_{t-1})p(x_{t-1})}{p(x_t)},p(x_t|x_{t-1})\sim N(\sqrt{\alpha_t}x_{t-1},\beta_t) p(xt−1∣xt)=p(xt)p(xt∣xt−1)p(xt−1),p(xt∣xt−1)∼N(αt xt−1,βt)
求解 p ( x t − 1 ) p(x_{t-1}) p(xt−1)和 p ( x t ) p(x_t) p(xt)不方便,所以
p ( x t − 1 ∣ x 0 , x t ) = p ( x t ∣ x t − 1 , x 0 ) p ( x 0 ∣ x t − 1 ) p ( x t − 1 ) p ( x t ∣ x 0 ) p ( x 0 ) = p ( x t ∣ x t − 1 ) p ( x t − 1 ∣ x 0 ) p ( x 0 ) p ( x t ∣ x 0 ) p ( x 0 ) = p ( x t ∣ x t − 1 ) p ( x t − 1 ∣ x 0 ) p ( x t ∣ x 0 ) \begin{aligned}p(x_{t-1}|x_0,x_t)&=\frac{p(x_t|x_{t-1},x_0)p(x_0|x_{t-1})p(x_{t-1})}{p(x_t|x_0)p(x_0)} \\ &=\frac{p(x_t|x_{t-1})p(x_{t-1}|x_0)p(x_0)}{p(x_t|x_0)p(x_0)} \\ &=\frac{p(x_t|x_{t-1})p(x_{t-1}|x_0)}{p(x_t|x_0)}\end{aligned} p(xt−1∣x0,xt)=p(xt∣x0)p(x0)p(xt∣xt−1,x0)p(x0∣xt−1)p(xt−1)=p(xt∣x0)p(x0)p(xt∣xt−1)p(xt−1∣x0)p(x0)=p(xt∣x0)p(xt∣xt−1)p(xt−1∣x0)
p ( x t − 1 ∣ x 0 , x t ) ∼ N ( 1 α t ( x t − β t 1 − α ‾ t ε ) , β t ( a − α ‾ t − 1 ) 1 − α ‾ t ) p(x_{t-1}|x_0,x_t)\sim N(\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{1-\sqrt{\overline\alpha_t}}\varepsilon),\frac{\beta_t(a-\overline\alpha_{t-1})}{1-\overline\alpha_t}) p(xt−1∣x0,xt)∼N(αt 1(xt−1−αt βtε),1−αtβt(a−αt−1))
DDIM构造 𝑝 ( 𝑥 𝑠 │ 𝑥 𝑘 , 𝑥 0 ) , 𝑠 < 𝑘 − 1 𝑝(𝑥_𝑠│𝑥_𝑘,𝑥_0 ),𝑠<𝑘−1 p(xs│xk,x0),s<k−1这是没有马尔科夫性质的,只有 p ( x k ∣ x s , x 0 ) p(x_k|x_s,x_0) p(xk∣xs,x0)需要重新求解,其他两项在DDPM中是已知形式的。由于没有马尔科夫性质,所以可以加速采样过程(在生成过程将原来的1000步采样减少到隔20步做一次采样,这样50次就可以把原本的1000次去噪完成了)。
𝑝 ( 𝑥 𝑠 ∣ 𝑥 𝑘 , 𝑥 0 ) = ( 𝑝 ( 𝑥 𝑘 ∣ 𝑥 𝑠 , 𝑥 0 ) 𝑝 ( 𝑥 s ∣ 𝑥 0 ) ) ( 𝑝 ( 𝑥 𝑘 ∣ 𝑥 0 ) ) , 𝑝 ( 𝑥 𝑡 ∣ 𝑥 0 ) ∼ 𝑁 ( α 𝑡 𝑥 𝑡 − 1 , β 𝑡 ) 𝑝(𝑥_𝑠|𝑥_𝑘,𝑥_0 )=\frac{(𝑝(𝑥_𝑘|𝑥_𝑠,𝑥_0 )𝑝(𝑥_s|𝑥_0 ))}{(𝑝(𝑥_𝑘|𝑥_0 ) )},𝑝(𝑥_𝑡|𝑥_0 )∼𝑁(\sqrt{\alpha_𝑡} 𝑥_{𝑡−1},\beta_𝑡) p(xs∣xk,x0)=(p(xk∣x0))(p(xk∣xs,x0)p(xs∣x0)),p(xt∣x0)∼N(αt xt−1,βt)
然后假设 𝑝 ( 𝑥 𝑠 ∣ 𝑥 𝑘 , 𝑥 0 ) ∼ 𝑁 ( 𝑘 𝑥 0 + 𝑚 𝑥 𝑘 , σ 2 𝐼 ) 𝑝(𝑥_𝑠|𝑥_𝑘,𝑥_0 )∼𝑁(𝑘𝑥_0+𝑚𝑥_𝑘,\sigma^2𝐼) p(xs∣xk,x0)∼N(kx0+mxk,σ2I)
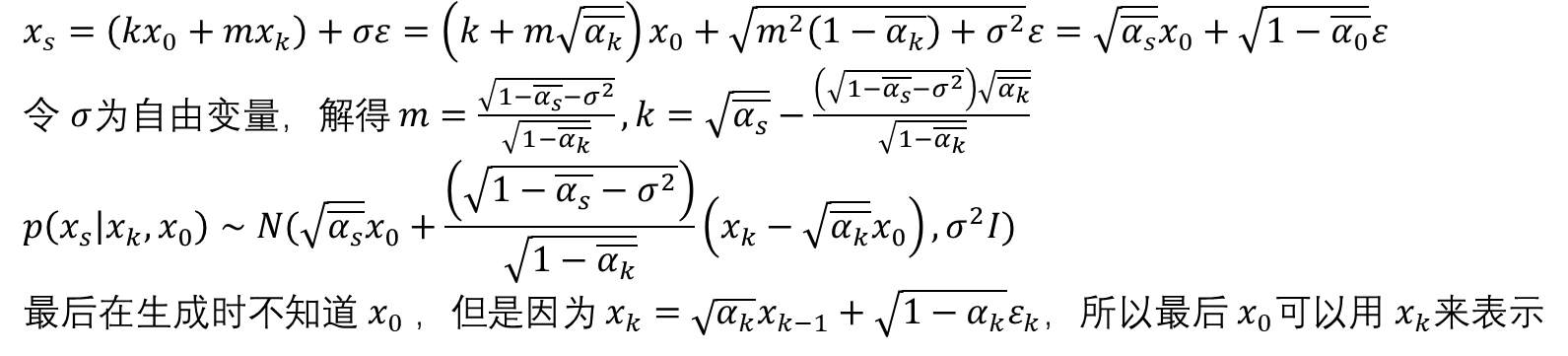
2 DiT
DiT在2022年由William Peebles, Saining Xie的论文Scalable Diffusion Models with Transformers提出
2.1 替换Unet
DiT将传统DDPM的Unet架构替换成了DiT Block,并且加入Adaptive LayerNorm Block取得了很好的结果。


左侧:训练条件潜在DiT模型(conditional latent DiT models), 潜在输入被分解成patch并通过几个DiT blocks处理。
本质就是噪声图片减掉预测的噪声以实现逐步复原
比如当输入是一张256x256x3的图片,对图片做切patch后经过投影得到每个patch的token,得到32x32x4的Noised Latent(即加噪的图片,在推理时输入直接是32x32x4的噪声),结合当前的Timestep t、Label y作为输入
经过N个Dit Block(基于transformer)通过mlp进行输出,从而得到噪声"Noise预测"以及对应的协方差矩阵,最后经过T个step采样,得到32x32x4的降噪后的latent
右侧:DiT blocks的细节,作者试验了标准transformer块的变体,这些变体通过自适应层归一化、交叉注意和额外输入token来加入条件,其中自适应层归一化效果最好。
自适应层归一化,即Adaptive layer norm (adaLN) block
鉴于自适应归一化层在GANs和具有U-Net骨干的扩散模型中的广泛使用,故用自适应层归一化(adaLN)替换transformer块中的标准层归一化层
不是直接学习维度方向的缩放和偏移参数 和 ,而是从 和类别标签的嵌入向量之和中回归它们
adaLN-Zero block
关于ResNets的先前工作发现,将每个残差块初始化为恒等函数是有益的。例如,Goyal等人发现,在每个块中将最终批量归一化尺度因子 γ零初始化可以加速大规模训练在监督学习设置中[13]
扩散U-Net模型使用类似的初始化策略,在任何残差连接之前将每个块的最终卷积层零初始化。 作者对adaLN DiT块的修改,它做了同样的事情。 除了回归 γ和 β,还回归在DiT块内的任何残差连接之前立即应用的维度方向的缩放参数 α
交叉注意力块
将t和c的嵌入连接成一个长度为二的序列,与图像token序列分开,transformer块被修改为:在多头自注意块之后,包含一个额外的多头交叉注意层,类似于LDM用于根据类标签进行条件处理的设计。 交叉注意力使模型增加了最多的Gflops,大约增加了15%的开销
上下文条件化(In-context conditionin)
将 和 的向量嵌入作为两个额外的token追加到输入序列中,与图像token无异地对待它们,这类似于ViTs中的 cls token,它允许使用标准ViT块而无需修改。 在最后一个块之后,从序列中移除条件token。 这种方法没有新增模型多少Gflops,可忽略
总结
本周阅读了两篇论文,还没有通过代码进行实践,下周将加强代码部分的实践。