MATLAB简介

Oakland University EGR 1400------工程与计算机科学领域的计算机问题

Part Ⅰ 工程程序(C+外教C#)
Part Ⅱ 科学计算(MATLAB简介)

MATLAB运行环境

MATLAB简介

MATLAB：中文意为矩阵实验室(Matrix Lab)，美国MathWorks出品的高端商业(付费)数学软件，基于C++开发，以数值分析、矩阵运算、数据可视化、建模仿真等方面见长。
MATLAB拥有丰富的生态，以工具箱(Toolbox)提供，涵盖科学计算、信号处理、图像处理、控制工程、人工智能、金融建模等各个前沿领域，是工业和科研界的"瑞士军刀"。
前沿应用：控制工程：飞行器、汽车、机器人系统设计，使用Simulink进行建模与仿真；数据分析与科学计算：处理大规模实验数据、算法验证、优化计算；数字信号处理与通信：滤波器设计、通信信号仿真；人工智能与机器学习：通过专门的工具箱快速搭建神经网络、训练模型。

特斯拉用MATLAB仿真电池管理系统，NASA用Simulink设计控制器。
可用于数学建模竞赛的模型建立求解与可视化。
进入美国"实体清单"的中国高校被禁止使用MATLAB，如哈工大、西工大、哈工程、北航等。常见替代方案包括Python、Octave等。

MATLAB窗口

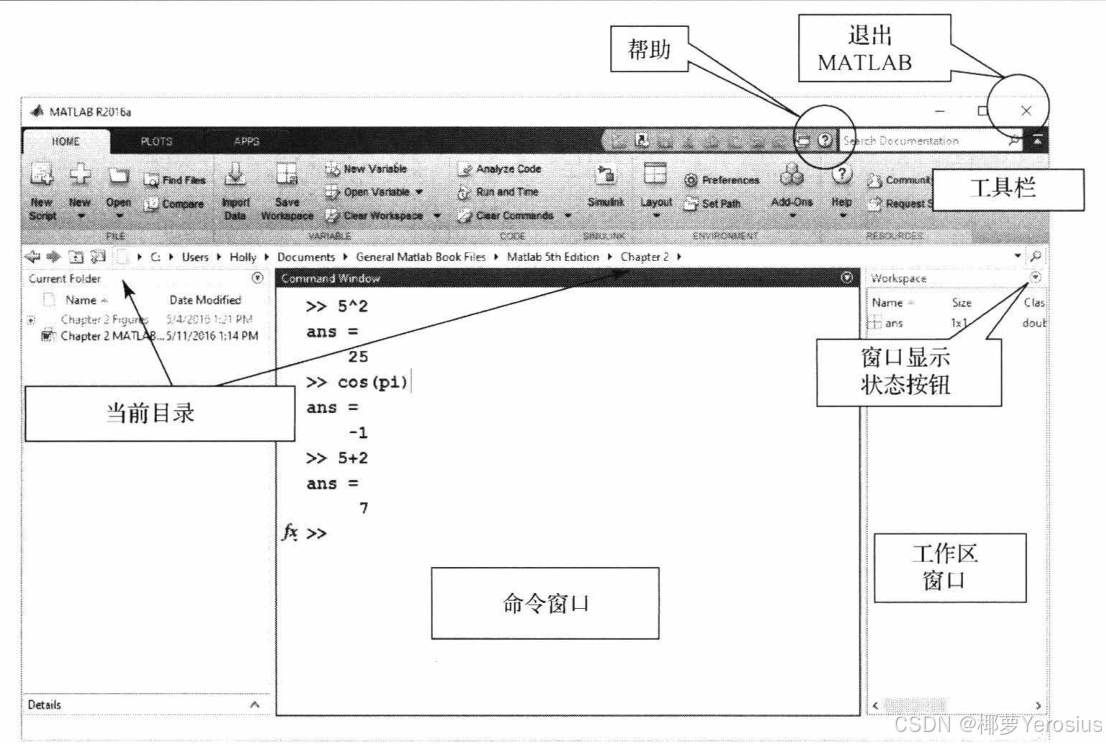
MATLAB是一门解释型语言。与Python相同，MATLAB也分为命令行模式和文件(.m)模式。
命令行模式：输入表达式后，立即返回其值，并继续读取输入，这一过程称为REPL(Read-Eval-Print Loop 阅读-执行-打印循环)。若要取消输出，则在命令后加;。对于较大规模或无关紧要的数据集，则必须取消输出以加快程序执行速度。
所有定义的变量，都被保存在工作区，在工作区能看到其信息。
清除命令行：clc；清除工作区：clear

变量、数据类型及基本I/O

变量

若不将表达式的值赋值给任意变量，则其将被赋值给默认变量ans。
变量需先定义后使用。变量名定义规则：
- 必须以字母开头，之后可以是任意字母、数字、下划线。变量名对大小写敏感，不能超过31个字符。
- 禁止使用内置关键字作为变量名，使用iskeyword查看MATLAB保留关键字。
- 允许占用内置变量和函数名作为变量名，使用which [符号名]查看当前符号所指向的是谁。使用clear [符号名]，通过清除工作区内特定变量，从而恢复系统默认指向。
- 两个重要无理数变量：pi(π\piπ)，e(eee)

数据类型及运算符

数据类型：整型、浮点型、复数(a+bi)
运算符：+，-，*，/，^
关系运算符：==，~=(MATLAB中的不等号)，>，>=，<，<=，关系运算为返回0或1的布尔表达式。使用find(布尔表达式)返回所有满足该条件的值。
逻辑运算：&/&&/and(&不具有短路效应，&&具有短路效应，下同)，|/||/or，~/not，xor(逻辑异或，MATLAB独有)，any(有0为真)，all(无0为真)

基本I/O

input(str)：输入，str为输入提示信息。
input(str,'s')：输入一个字符串
disp(x)：输出；也可采用disp([x y])的形式对多个变量进行输出，需要特别注意当输出包含字符串时，必须将其他内容也转为字符串，如数字采用num2str转换为字符串。
fprintf：格式化输出，其与C语言中printf行为一致。

向量及矩阵代数

向量

向量：分为行向量和列向量。MATLAB中可使用以下方法创建向量：
- 直接输入：使用[]创建一个向量或矩阵。在向量中，;代表分行符，,代表分列符。如[2,3,4]或[2 3 4]代表创建行向量(2,3,4)(2,3,4)(2,3,4)，[2;3;4]代表创建行向量(234)\begin{pmatrix}2\\3\\4\end{pmatrix} 234 。一般情况下，,用空格代替。
  也可输入其他向量名，如A=[2 3 4]，B=[A A]，则B=(2,3,4,2,3,4)B=(2,3,4,2,3,4)B=(2,3,4,2,3,4)。
- 冒号法：起点:步长:终点，闭区间。
- 函数linspace(起点,终点,元素个数)：通过指定起点到终点间的元素个数，由MATLAB自动计算出线性等距 步长创建向量，即分量间每次加一样多的等差数列。
- 函数logspace(起点,终点,元素个数)：通过指定10起点10^{起点}10起点到10终点10^{终点}10终点间的元素个数，由MATLAB自动计算出对数等距 步长创建向量，即分量间每次乘一样多 的等比数列。
  logspace的原理：先按原参数生成linspace，再将各个分量xix_ixi替换为10xi10^{x_i}10xi。
向量尺寸：size()函数，返回一个行向量，第一个分量为行数，第二个分量为列数。
向量中分量的访问：(注：MATLAB中向量分量下标从1开始)
- 直接访问：向量名(i)：访问 xix_ixi。
- 切片：向量名(i:j)：切片出子向量(xi,xi+1,...,xj−1,xj)(x_i,x_{i+1},\dots ,x_{j-1},x_j)(xi,xi+1,...,xj−1,xj)，步长为1。
- 切片：向量名(i:步长:j)：按照步长切片出子向量。
- 逻辑访问：向量名(布尔表达式)，其中布尔表达式形如：向量名>=x等。返回满足布尔表达式的所有元素所组成的向量，向量方向与原向量相同。等价于向量名(find(布尔表达式))。
向量代数：
- 向量的转置：向量名'
- 线性运算：即+，-，*，/
  - 向量与数运算：向量中每一个分量均与该数运算
  - 向量与向量运算：
    - 对于+，-：对应分量做运算，要求两向量大小必须相等。
    - 对于*：做向量乘法 ABABAB，要求 AAA 的列数必须等于 BBB 的行数。若想逐元素运算，使用.*或./。
- 其他运算：基本初等函数均能作用于向量，为逐元素计算。
- 向量的点积：dot(a,b)，等价于aTba^TbaTb。
- sum：对向量为各分量之和；prod：对向量为各分量之积
- cumsum：对向量做前缀和；cumprod：对向量做前缀积

矩阵

创建矩阵：
- 直接输入：矩阵可视为若干个行向量拼接而成，创建矩阵时使用;分隔行即可。
  matlab 复制代码
```
A=[
1 2 3;
4 5 6;
7 8 9
]
```
  也可输入其他向量及矩阵名，如A=[2 3 4]，B=[A';A']，则B=(223344)B=\begin{pmatrix} 2 & 2 \\ 3 & 3 \\ 4 & 4 \end{pmatrix}B= 234234 。
- MATLAB在内存中存储矩阵为按列存储。
- .m文件：将矩阵保存到.m文件中，在命令行中输入该文件名，导入文件中的矩阵。
- load命令：创建纯文本文件，一个文件只能代表一个矩阵。在文件中直接写矩阵的内容，使用load 文件名加载该矩阵。
矩阵尺寸：size。返回一个行向量，第一个分量为行数，第二个分量为列数。
矩阵元素访问：(注：MATLAB中矩阵下标从1开始)
- 按行列访问：矩阵名(行号,列号)
- 切片访问：行号和列号参数中可使用切片操作：起点:步长:终点，若不指定步长则默认为1。也可采用一个单独的:表示所有。使用end关键字代表该维度上的最后一项。
- 按线性索引访问：矩阵名(索引)，其中编号为从上到下，从左到右编号。
- 逻辑访问：矩阵名(布尔表达式)，其中布尔表达式形如矩阵名>=x。返回所有满足布尔表达式的元素所组成的列向量 。等价于矩阵名(find(布尔表达式))。
特殊的矩阵：
- eye(n)：创建 nnn 阶单位阵。（单位阵：主对角线为1，其余均为0的方阵）
- ones(n,m)：创建 n×mn\times mn×m 的全1矩阵；ones(n)：创建 nnn 阶全1方阵；ones(size(A))：创建与A尺寸相同的全1矩阵。
- zeros(n,m)：创建 n×mn\times mn×m 的全0矩阵；zeros(n)：创建 nnn 阶全0方阵；zeros(size(A))：创建与A尺寸相同的全0矩阵。
- rand(n,m)：创建 n×mn\times mn×m 的元素在[0,1][0,1][0,1]区间内的随机矩阵；rand(size(A))：创建与A尺寸相同的随机矩阵。
- magic(n)：创建 nnn 阶的魔方方阵。(魔方方阵：每行，每列，主副对角线元素之和均相等的方阵。可证1阶魔方阵唯一，不存在2阶魔方阵，n≥3n\ge 3n≥3阶魔方阵数量巨大。在MATLAB中，每阶只能构造出一个魔方阵。)
- vander(x)：以向量 xxx 创建范德蒙德矩阵。(范德蒙德矩阵：形如 [x1m⋯x11x10x2m⋯x21x20⋮⋱⋮⋮xnm⋯xn1xn0]\begin{bmatrix} x_1^m & \cdots & x_1^1 & x_1^0\\ x_2^m & \cdots & x_2^1 & x_2^0\\ \vdots & \ddots & \vdots & \vdots\\ x_n^m & \cdots & x_n^1 & x_n^0 \end{bmatrix} x1mx2m⋮xnm⋯⋯⋱⋯x11x21⋮xn1x10x20⋮xn0 的矩阵，其中低次幂在右，高次幂在左。)
- hilb(n)：创建 nnn 阶希尔伯特矩阵。(希尔伯特矩阵：每一项 Hi,j=1i+j−1H_{i,j}=\frac{1}{i+j-1}Hi,j=i+j−11 的矩阵)
矩阵变维：reshape(X,n,m)：将X重排为n行m列矩阵。重排规则为从上到下，从左到右。
翻转矩阵：rot90(A)：将矩阵 AAA 逆时针旋转 90°90\degree90°；rot90(A,k)：将矩阵 AAA 逆时针旋转 k⋅90°k\cdot90\degreek⋅90°；fliplr(A)：将矩阵 AAA 左右(left & right)翻转；flipud(A)：将矩阵 AAA 上下(up & down)翻转。
矩阵代数：
- +，-，*：与线性代数运算法则及要求一致。若想逐元素运算，使用.*或./。
- /：MATLAB中特有运算，A/B=AB−1A/B=AB^{-1}A/B=AB−1。
- A'：矩阵转置 ATA^TAT
- diag(A)：提取矩阵 AAA 主对角线上的元素；trace(A)：矩阵 AAA 的迹。
- det(A)：方阵的行列式
- inv(A)：方阵AAA的逆矩阵
- sum：对矩阵为各列之和；prod：对矩阵为各列之积
- cumsum：对矩阵做各列前缀和；cumprod：对矩阵做各列前缀积

常用函数

帮助函数：help
运算函数：
- rem(a,b)：取余
- sign：符号函数
基本初等函数(反对幂指三)：
- sqrt(x)：x\sqrt xx ，nthroot(x,n)：xn\sqrt[n]{x}nx
- exp：exe^xex
- log：ln⁡\lnln，log10：lg⁡\lglg，log2：log⁡2\log_2log2
- 三角及反三角函数：
  - deg2rad：角度制转弧度制，rad2deg：弧度制转角度制
  - sin，asin；sind，asind：弧度制/角度制下的正弦及反正弦
  - cos，acos；cosd，acosd：弧度制/角度制下的余弦及反余弦
  - tan，atan，atan2(y,x)；tand，atand，atan2d(y,x)：弧度制/角度制下的正切及反正切，其中atan返回值为[−π2,π2][-\frac{\pi}{2},\frac{\pi}{2}][−2π,2π]，atan2返回值是[−π,π][-\pi,\pi][−π,π]。
  - cot，acot；cotd，acotd：弧度制/角度制下的余切及反余切
  - sec，asec；secd，asecd：弧度制/角度制下的正割及反正割
  - csc，acsc；cscd，acscd：弧度制/角度制下的余割及反余割
- 双曲及反双曲函数：
  - sinh，asinh：双曲正弦及反双曲正弦
  - cosh，acosh：双曲余弦及反双曲余弦
  - tanh，atanh：双曲正切及反双曲正切
  - coth，acoth：双曲余切及反双曲余切
  - sech，asech：双曲正割及反双曲正割
  - csch，acsch：双曲余割及反双曲余割
舍入函数：
- round：四舍五入
- fix：向 000 取整
- floor：向下取整
- ceil：向上取整
数论：
- factor：分解质因数
- gcd(x,y)：最大公约数
- lcm(x,y)：最小公倍数
- primes(x)：求 <x<x<x 的所有质数
- isprime(x)：判断 xxx 是否为质数，返回一个布尔值
数理统计：
- max/min：求向量/矩阵中的最大/最小值，默认返回一个参数。第二个参数为最值的下标，需使用形如[a,idx]=max(x)的形式显式调用。
- mean：均值
- median：中位数
- mode：众数
- std：标准差
- var：方差
排序：sort：对向量为升序排列，对矩阵为按列升序排列；sort(x,'descend')降序排列。

流程控制

选择结构

if语句

单分支结构：
matlab 复制代码
```
if condition
	% command
end
```
双分支结构：

matlab 复制代码

if condition
	% command1
else
	% command2
end

多分支结构：

matlab 复制代码

if condition1
	% command1
elseif condition2
	% command2
else
	% command3
end

switch...case语句

matlab 复制代码

switch variable
case condition1
    % command1
...
case condition n
    % command n
otherwise
    % command n+1

实例------menu函数：menu('提示', '选项1', '选项2', ...)，参数中从提示开始从0顺次编号，返回值即为点选的选项编号。

循环结构

while循环：
matlab 复制代码
```
while condition
	% command
end
```
for循环：
matlab 复制代码
```
for 迭代变量 = 可迭代对象
	% command
end
```
可迭代对象可以为向量(包括冒号运算符 生成的)、矩阵。在迭代矩阵时，为列优先原则。

Python中用range进行的范围迭代，在MATLAB中为使用冒号运算符代替。
跳转语句：break和continue。

文件及自定义函数

MATLAB文件：.m，分为命令文件与函数文件。函数文件不能独立运行，必须被命令文件调用运行。
在MATLAB中，每个函数必须被定义为独立文件，文件名必须为函数名。
- 设当前函数名为f，参数为x，返回值为y，则函数头为：
  matlab 复制代码
```
function y=f(x)
	% command
end
```
- 函数可接受多个形参，也可有多个返回值：
  matlab 复制代码
```
function [a,b,c,...]=f(x,y,z,...)
	% command
end
```
  调用时返回值取决于调用方式。若为f(x)为只接收第一个返回值，[a,b]=f(x)为接收前两个返回值。必须按顺序接收返回值，不能跳过。若无需接收，则需用~占位(相当于C++中的ignore和Python的_)。
- 若无返回值且无形参，则直接写作：
  matlab 复制代码
```
function f()
	% command
end
```
- 注：函数体需以end结束。
函数名命名规则：必须以字母开头，可包含字母、数字、下划线，不能使用保留关键字。
行内注释：%；块注释：%{ }%。help命令原理即为打印函数文件开头且连续的注释。
查看参数数量：nargin。若在函数文件中使用，则为接收到的形参数量。
变是的作用域：命令文件中变量为基工作区变量，其对函数不可见；函数中的变量为局部工作区变量，其生存周期仅限于该函数；使用global标签所定义的变量为全局工作区变量，其对所有工作区可见，global标签需先声明后使用。
type(s)：查看文件内容，其中s为函数文件名。

可视化

基本二维绘图

可视化的层级：
- Canvs(画布)：底层隐藏画布
- Figure(图)：图的独立窗口
- Subplot(子图)：画布上的子图
- Plot(线)：图上绘制的真实图形
使用clf命令清除当前Figure；使用close(x)关闭第x个Figure；使用close all关闭所有Figure。

二维笛卡尔坐标系

plot：基础绘图命令，为二维笛卡尔坐标系下的绘图。调用时会打开一个新的Figure。使用figure(x)新建第 xxx 个Figure。
- plot(x)：当 xxx 为向量时，以分量下标为横坐标，分量值为纵坐标绘图；当 XXX 为矩阵时，按列进行绘制，以行下标为横坐标，元素值为纵坐标绘图。
- plot(x,y)：当 xxx 和 yyy 是同维向量时，以 (xi,yi)(x_i,y_i)(xi,yi) 绘图。
- plot(x1,y1,x2,y2,...)：绘制多条曲线，等价于hold on并顺序执行多个plot。
- plot(x,y,s)：s为样式控制字符串(以单引号包围)，用于控制线条颜色、粗细，数据点类型、形状等，不同选项可互相叠加。
- plot(x1,y1,s1,x2,y2,s2,...)：绘制多条曲线，并进行样式控制。
  
  样式控制字符串可包含以下内容：
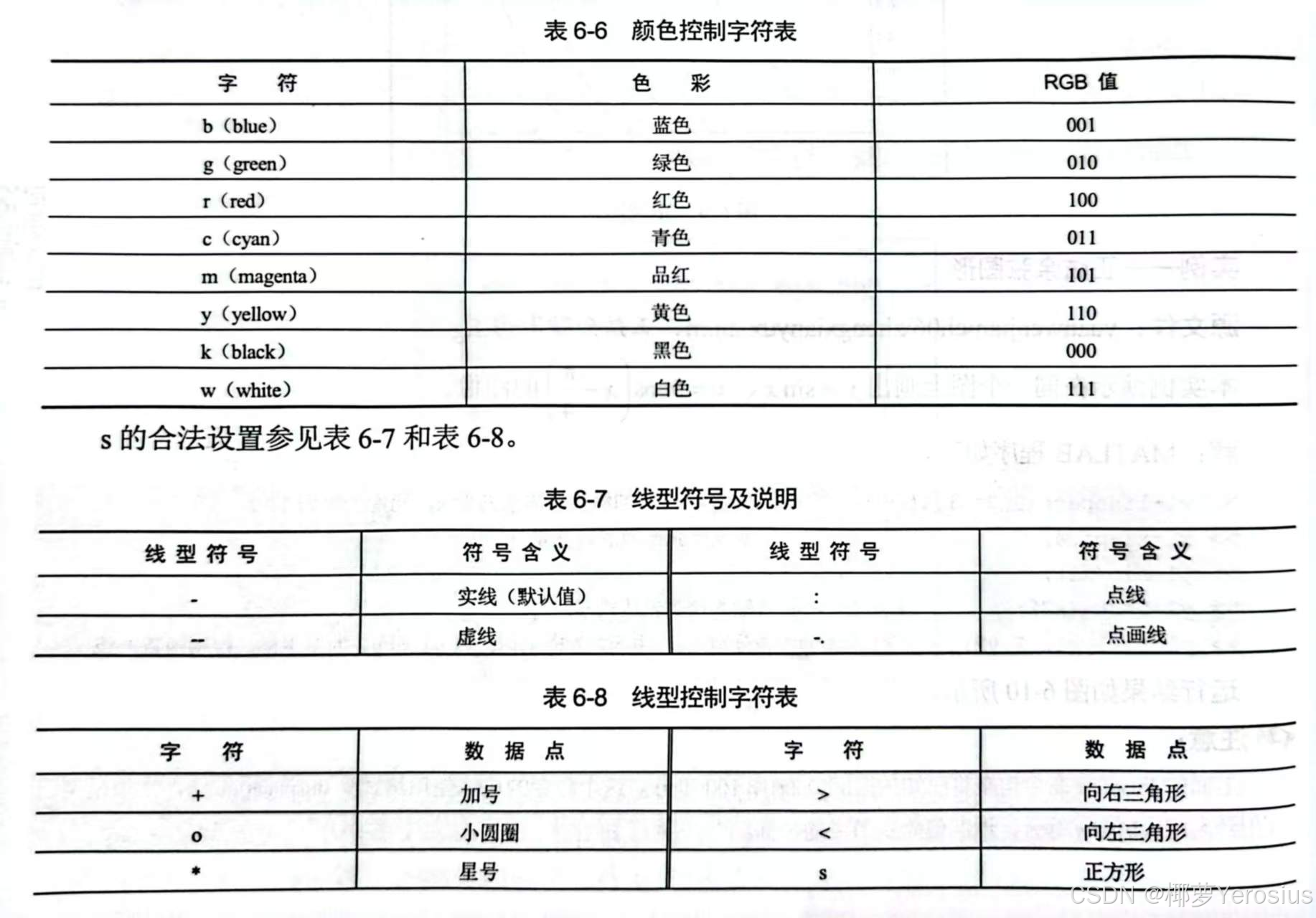
subplot(n,m,p)：将当前Figure分割为 n×mn\times mn×m 个子图区域，并将第 ppp 个子图用作当前子图。子图编号从左到右，从上到下递增。
在同一子图上进行plot，则会进行覆盖。使用hold on从而保持该子图中先前绘图，实现追加绘图。
fplot(f,range)：在给定区间range内绘制一元函数 f(x)f(x)f(x)。例：fplot(@(x) sin(x), [0, 10]);为绘制 sin⁡x\sin xsinx 在 [1,10][1,10][1,10] 内的函数图像。其中@(x) sin(x)为匿名函数，@为函数

句柄，(x)为输入参数。

极坐标系

polar(theta,rho)：极坐标系下的以 θ\thetaθ 为极角，ρ\rhoρ 为极径进行绘图

绘图标注

axis(xmin,xmax,ymin,ymax)：设置 x,yx,yx,y 轴最小值和最大值。
area(x,y)：绘制面积图
title(s)：添加题注，其中s为单引号字符串
xlabel(s)：添加 xxx 轴标签；ylabel(s)：添加 yyy 轴标签。其中s为单引号字符串。

注：MATLAB中字符串使用单引号标注。若要在字符串中使用单引号，使用两个单引号进行转义。字符串中支持简化的 TeX\TeXTEX 语法。
grid on：对笛卡尔坐标系绘制网格图
legend(s1,s2,...)：按照plot的顺序，为曲线添加图例，其中s1,s2代表字符串。

保存图形

saveas(gcf,s)：保存当前Figure到s，其中s是图片路径。可选扩展名有.png、.jpg、.fig等。