Day32 深入理解SHAP图

一、知识点

1. SHAP库简介

目标：理解复杂机器学习模型（尤其是 "黑箱" 模型，如随机森林、梯度提升树、神经网络等）为什么会对特定输入做出特定预测。SHAP 提供了一种统一的方法来解释模型的输出。核心思想：合作博弈论中的 Shapley 值SHAP (SHapley Additive exPlanations) 的核心基于博弈论中的 Shapley 值概念。想象一个合作游戏：

玩家 (Players): 模型的特征 (Features) 就是玩家。
游戏 (Game): 目标是预测某个样本的输出值。
合作 (Coalition): 不同的特征子集可以 "合作" 起来进行预测。
奖励 / 价值 (Payout/Value): 某个特征子集进行预测得到的值。
目标：如何公平地将最终预测结果（相对于平均预测结果的 "收益"）分配给每个参与的特征（玩家）？

Shapley 值的计算思路（概念上）：为了计算一个特定特征（比如 "特征 A"）对某个预测的贡献（它的 Shapley 值），SHAP 会考虑：

所有可能的特征组合（子集 / 联盟）：从没有特征开始，到包含所有特征。

特征 A 的边际贡献：对于每一个特征组合，比较 "包含特征 A 的组合的预测值" 与 "不包含特征 A 但包含其他相同特征的组合的预测值" 之间的差异。这个差异就是特征 A 在这个特定组合下的 "边际贡献"。

加权平均：Shapley 值是该特征在所有可能的特征组合中边际贡献的加权平均。权重确保了分配的公平性。

2. SHAP 的关键特性（加性解释 - Additive Explanations）

SHAP 的一个重要特性是加性 (Additive)。这意味着：・基准值 (Base Value / Expected Value): 这是模型在整个训练（或背景）数据集上的平均预测输出。可以理解为没有任何特征信息时的 "默认" 预测。・SHAP 值之和：对于任何一个样本的预测，所有特征的 SHAP 值加起来，再加上基准值，就精确地等于该样本的模型预测值。模型预测值 (样本 X) = 基准值 + SHAP 值 (特征 1) + SHAP 值 (特征 2) + ... + SHAP 值 (特征 N)

为什么会生成 shap_values 数组？根据上述原理，SHAP 需要为每个样本的每个特征计算一个贡献值（SHAP 值）；

解释单个预测：SHAP 的核心是解释单个预测结果。

特征贡献：对于这个预测，我们需要知道每个特征是把它往 "高" 推了，还是往 "低" 推了（相对于基准值），以及推了多少。

数值化：这个 "推力" 的大小和方向就是该特征对该样本预测的 SHAP 值。

因此：

对于回归问题：

模型只有一个输出。
对 n_samples 个样本中的每一个，计算 n_features 个特征各自的 SHAP 值
这就自然形成了形状为 (n_samples, n_features) 的数组。shap_values [i, j] 代表第 i 个样本的第 j 个特征对该样本预测值的贡献。

对于分类问题：

模型通常为每个类别输出一个分数或概率。○ SHAP 需要解释模型是如何得到每个类别的分数的。
因此，对 n_samples 个样本中的每一个，分别为每个类别计算 n_features 个特征的 SHAP 值。最常见的组织方式是返回一个列表，列表长度等于类别数。列表的第 k 个元素是一个 (n_samples, n_features) 的数组，表示所有样本的所有特征对预测类别 k 的贡献。○ shap_values [k][i, j] 代表第 i 个样本的第 j 个特征对该样本预测类别 k 的贡献。

总结:SHAP 通过计算每个特征对单个预测（相对于平均预测）的边际贡献（Shapley 值），提供了一种将模型预测分解到每个特征上的方法。这种分解对于每个样本和每个特征（以及分类问题中的每个类别）都需要进行，因此生成了我们看到的 shap_values 数组结构。

3. shap 的维度要求

分类问题和回归问题输出的 shap_values 的形状不同。

分类问题：shap_values.shape = (n_samples, n_features, n_classes)

回归问题：shap_values.shape = (n_samples, n_features)

数据维度的要求将是未来学习神经网络最重要的东西之一。

二、实例化

本数据来源于sklearn库的回归问题load_diabetes糖尿病数据集

1. 前置代码

python 复制代码

# 1. 导入必要的库
import pandas as pd  # 用于将数据集转为DataFrame，方便数据查看与操作
import numpy as np   # 用于数值计算
import matplotlib.pyplot as plt  # 用于绘制可视化图表
import time  # 用于记录代码运行耗时
from sklearn.datasets import load_diabetes  # 加载sklearn自带的糖尿病回归数据集（预测疾病进展）
from sklearn.model_selection import train_test_split  # 划分训练集和测试集
from sklearn.ensemble import RandomForestRegressor  # 随机森林回归模型（替换原分类模型）
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score  # 回归任务专属评估指标
import shap  # 用于模型解释的SHAP库
import warnings
warnings.filterwarnings("ignore")  # 忽略代码运行中的警告信息

# 设置中文字体（解决matplotlib中文显示乱码问题）
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号

diabetes = load_diabetes()  
X = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)  
y = pd.Series(diabetes.target, name='disease_progress')

# 检查并处理缺失值（sklearn自带数据集通常无缺失，此处为通用示例）
print("数据集各列缺失值数量：")
print(X.isnull().sum())  # 统计每列的缺失值个数


# 划分训练集与测试集（8:2比例）
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42  # test_size=0.2表示20%为测试集；random_state固定随机划分方式
)

2. 基线模型

python 复制代码

# 训练随机森林回归模型并记录耗时
from sklearn.ensemble import RandomForestClassifier #随机森林分类器

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score # 用于评估分类器性能的指标
from sklearn.metrics import classification_report, confusion_matrix #用于生成分类报告和混淆矩阵
import warnings #用于忽略警告信息
warnings.filterwarnings("ignore") # 忽略所有警告信息
# --- 1. 默认参数的随机森林 ---
# 评估基准模型，这里确实不需要验证集
print("--- 1. 默认参数随机森林 (训练集 -> 测试集) ---")
import time # 这里介绍一个新的库，time库，主要用于时间相关的操作，因为调参需要很长时间，记录下会帮助后人知道大概的时长
start_time = time.time() # 记录开始时间
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train) # 在训练集上训练
rf_pred = rf_model.predict(X_test) # 在测试集上预测
end_time = time.time() # 记录结束时间

print(f"训练与预测耗时: {end_time - start_time:.4f} 秒")
print("\n默认随机森林 在测试集上的分类报告：")
print(classification_report(y_test, rf_pred))
print("默认随机森林 在测试集上的混淆矩阵：")
print(confusion_matrix(y_test, rf_pred))

3. 评估回归模型性能

python 复制代码

# 评估回归模型性能（使用回归专属指标）
mae = mean_absolute_error(y_test, y_pred)  # 平均绝对误差：预测值与真实值的平均绝对差异
mse = mean_squared_error(y_test, y_pred)  # 均方误差：预测值与真实值差异的平方的平均值
r2 = r2_score(y_test, y_pred)  # R²系数：衡量模型能解释数据变异的比例（越接近1越好）

print("\n回归模型在测试集上的评估结果：")
print(f"平均绝对误差（MAE）: {mae:.4f}")
print(f"均方误差（MSE）: {mse:.4f}")
print(f"R²系数: {r2:.4f}")

4. 计算SHAP值并可视化

python 复制代码

#  用SHAP解释回归模型
explainer = shap.TreeExplainer(rf_reg)  # 初始化树模型专用的SHAP解释器
shap_values = explainer.shap_values(X_test)  # 计算测试集的SHAP值（回归任务是二维数组：样本数×特征数）

4.1 SHAP特征重要性条形图

python 复制代码

print("\n--- 1. SHAP特征重要性条形图 ---")
shap.summary_plot(shap_values, X_test, plot_type="bar", show=False)
plt.title("SHAP特征重要性（条形图）")
plt.show()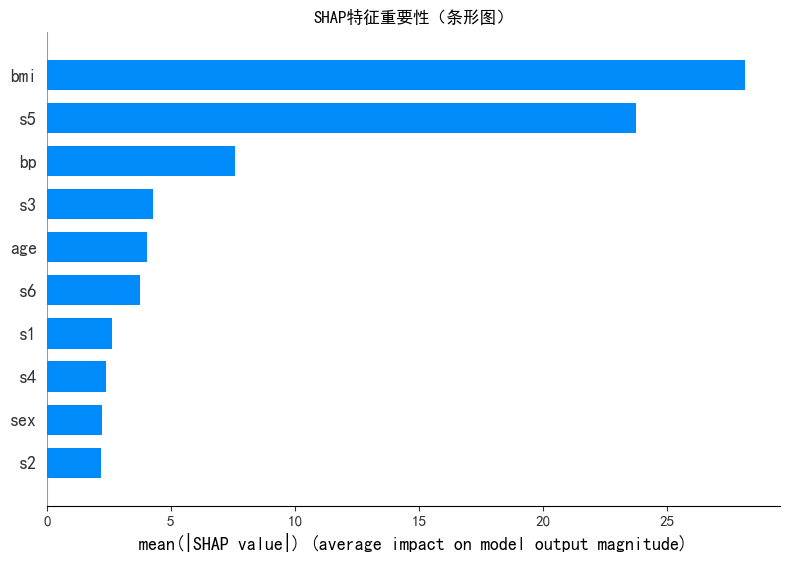

这个图能帮我们快速识别模型做预测时 "主要依赖哪些特征"：

模型的预测结果，主要由bmi和s5这两个特征决定；

sex、s2等特征的影响非常小，模型几乎不会 "依赖" 这些特征做决策。

总结：该模型的预测逻辑高度依赖bmi和s5，这两个是解释模型结果的核心特征。

4.2 SHAP特征重要性蜂巢图

python 复制代码

print("--- 2. SHAP特征重要性蜂巢图 ---")
shap.summary_plot(shap_values, X_test, plot_type="violin", show=False, max_display=10)  # 仅展示前10个重要特征
plt.title("SHAP特征重要性（蜂巢图）")
plt.show()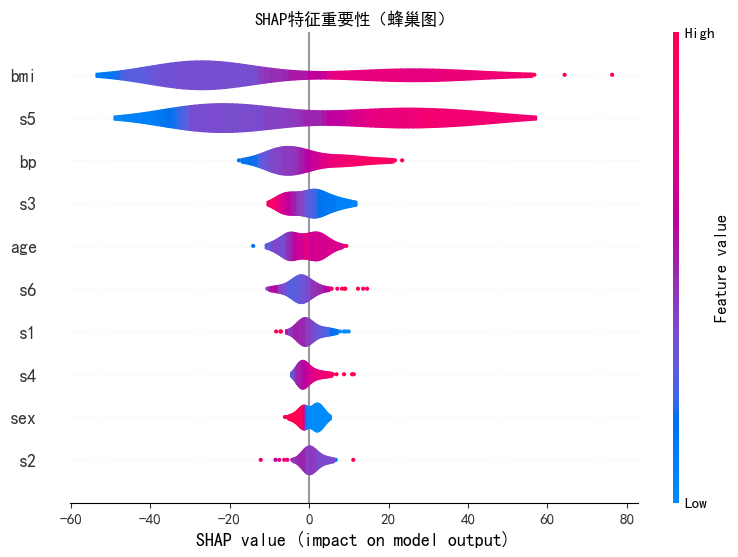

bmi（最核心特征） ：红色点（bmi 值高）对应的 SHAP 值是大正值 ，蓝色点（bmi 值低）对应的是负值。→ 结论：bmi 值越高，越会显著推高 模型的预测结果；bmi 值越低，越会拉低预测结果。

s5（次核心特征） ：红色点（s5 值高）对应 SHAP 正值，蓝色点（s5 值低）对应 SHAP 负值。→ 结论：s5 值越高，会推高预测结果；s5 值越低，会拉低预测结果。

bp（中等重要特征） ：红色点（bp 值高）对应的 SHAP 值是正值。→ 结论：bp 值越高，会推高预测结果。

其他特征（如age、s6等）：它们的 SHAP 值绝对值更小（影响更弱），但也能看到规律（比如age的蓝色点对应负值，红色点对应正值）------ 特征值高低与 SHAP 值的正负方向一致，但影响幅度远小于bmi和s5。

4.3 SHAP依赖图

python 复制代码

# 1.1 单特征依赖图（以影响最大的'bmi'特征为例）
print("--- SHAP依赖图（bmi特征） ---")
shap.dependence_plot(
    "bmi",  # 要分析的特征名
    shap_values,  # 测试集的SHAP值
    X_test,  # 测试集特征数据
    show=False,  # 不直接显示，后续自定义标题
    alpha=0.8,  # 点的透明度（避免重叠）
    color="#2E86AB"  # 点的颜色
)
plt.title("BMI特征的SHAP依赖图（影响疾病进展）", fontsize=12)
plt.xlabel("BMI特征值", fontsize=10)
plt.ylabel("BMI特征的SHAP值（影响程度）", fontsize=10)
plt.show()


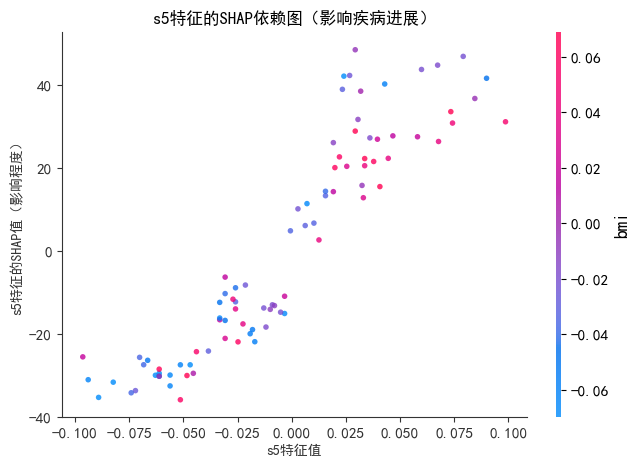
print("--- SHAP依赖图（s5特征） ---")
shap.dependence_plot(
    "s5",  # 要分析的特征名
    shap_values,  # 测试集的SHAP值
    X_test,  # 测试集特征数据
    show=False,  # 不直接显示，后续自定义标题
    alpha=0.8,  # 点的透明度（避免重叠）
    color="#C92020"  # 点的颜色
)
plt.title("s5特征的SHAP依赖图（影响疾病进展）", fontsize=12)
plt.xlabel("s5特征值", fontsize=10)
plt.ylabel("s5特征的SHAP值（影响程度）", fontsize=10)
plt.show()

# 1.2 带交互特征的依赖图（bmi为主特征，s5为交互特征）
print("--- SHAP依赖图（bmi + s5交互） ---")
shap.dependence_plot(
    "bmi",
    shap_values,
    X_test,
    interaction_index="s5",  # 叠加s5特征作为颜色区分
    show=False,
    cmap="viridis"  # 颜色映射方案
)
plt.title("BMI特征的SHAP依赖图（颜色区分s5特征值）", fontsize=12)
plt.show()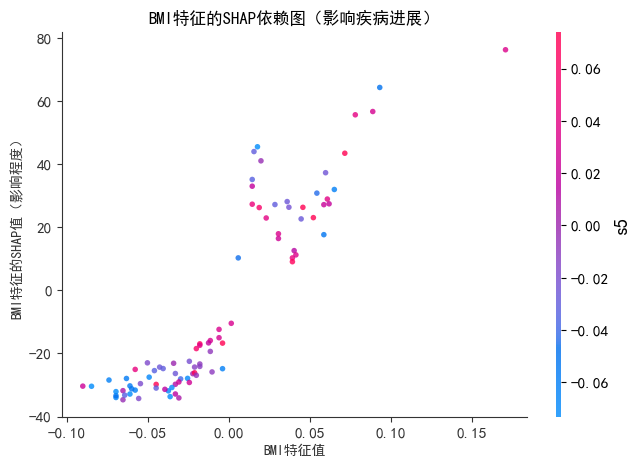

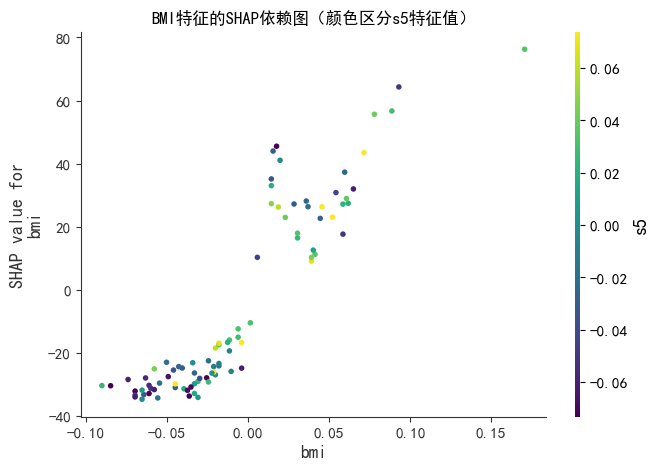
4.4 SHAP力图

python 复制代码

# 单个样本的力图（以测试集第0个样本为例）
print("--- SHAP力图（测试集第0个样本） ---")
# 计算基准值（所有样本的平均预测值）
base_value = explainer.expected_value
# 绘制力图（jupyter/notebook中用shap.plots.force更美观，本地用matplotlib兼容版）
shap.force_plot(
    base_value,  # 基准值
    shap_values[0, :],  # 第0个样本的SHAP值
    X_test.iloc[0, :],  # 第0个样本的特征值
    matplotlib=True,  # 用matplotlib渲染（本地运行必备）
    show=False,
    figsize=(15, 4),  # 图的尺寸
    text_rotation=0  # 文字旋转角度
)
plt.title("单个样本的SHAP力图（第0个测试样本）", fontsize=12)
plt.tight_layout()
plt.show()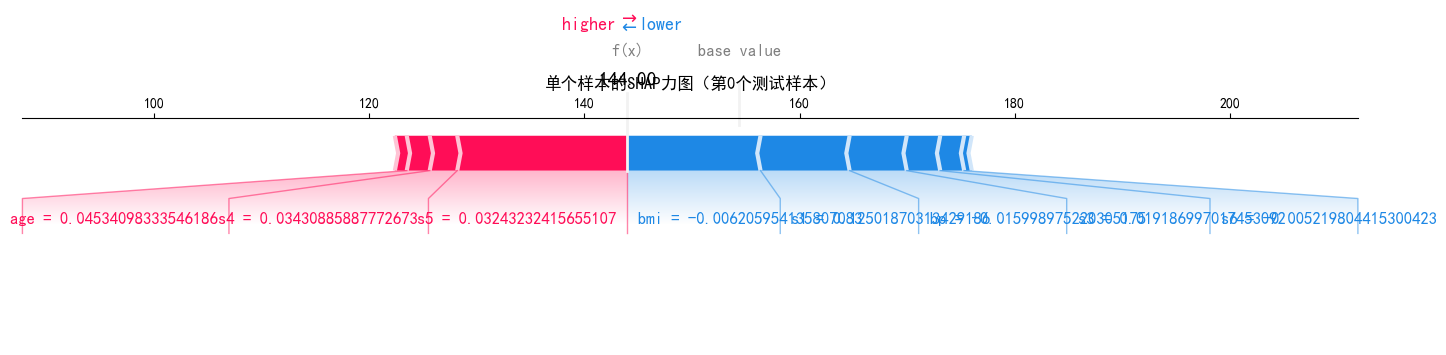

python 复制代码

import shap
shap.initjs()  # 核心：加载 SHAP 所需的 JS 库

# 步骤 2：重新运行你的 force_plot 代码（批量样本无需 matplotlib=True）
base_value = explainer.expected_value  # 回归/分类的基准值
force_plot_html = shap.force_plot(
    base_value,
    shap_values[:100, :],  # 前100个样本的SHAP值
    X_test.iloc[:100, :],
    show=False
)
force_plot_html  # 直接输出，此时 JS 已加载，可正常显示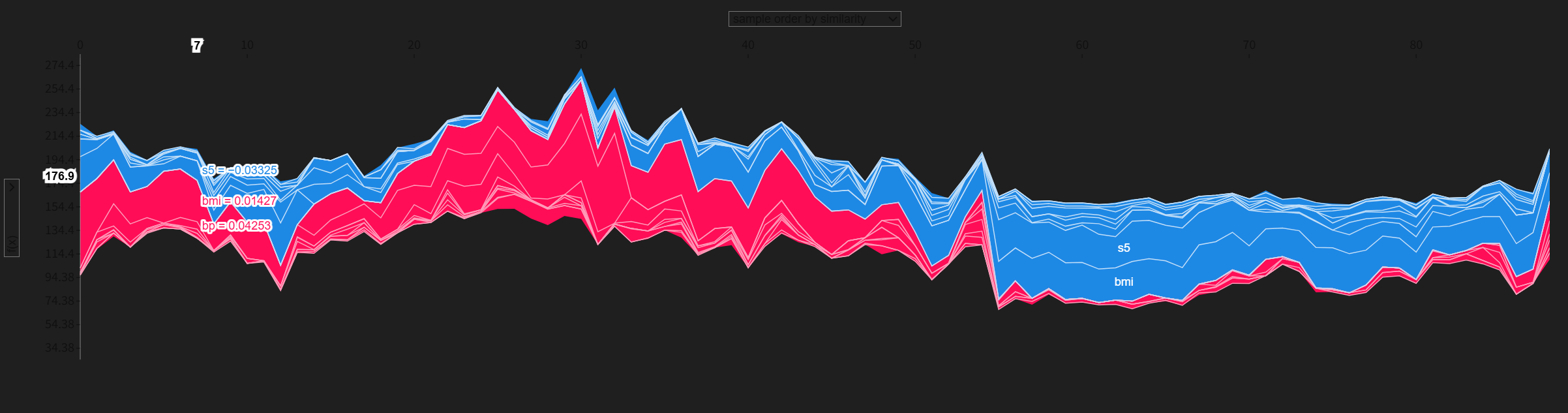

4.5 SHAP瀑布图

python 复制代码

print("--- SHAP瀑布图（测试集第0个样本） ---")
shap.plots.waterfall(
    shap.Explanation(
        values=shap_values[0],  # 第0个样本的SHAP值
        base_values=base_value,  # 基准值
        data=X_test.iloc[0],  # 第0个样本的特征值
        feature_names=X_test.columns  # 特征名
    ),
    max_display=10,  # 仅展示前10个核心特征
    show=False
)
plt.title("单个样本预测结果的SHAP瀑布图", fontsize=12)
plt.tight_layout()
plt.show()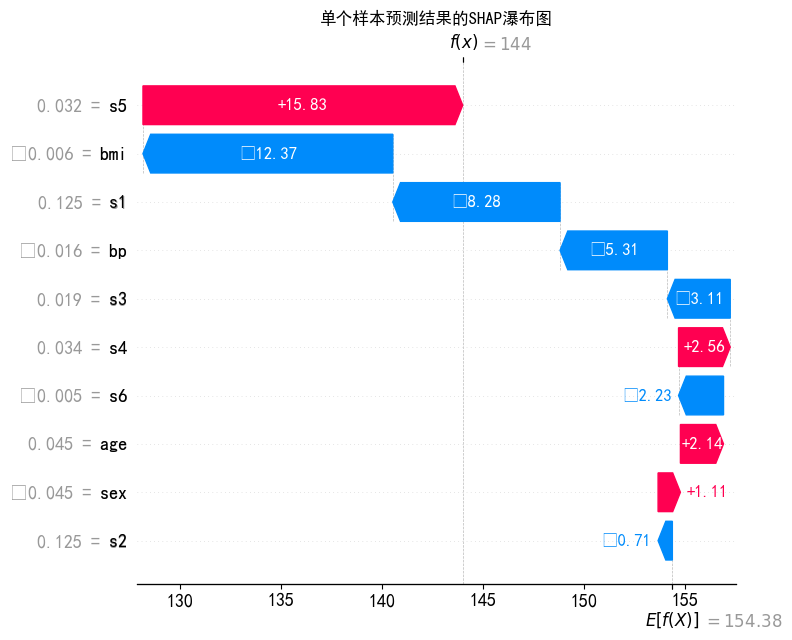

4.6 SHAP决策图

python 复制代码

# 4.1 单个样本的决策图
print("--- SHAP决策图（第0个样本） ---")
shap.decision_plot(
    base_value,
    shap_values[0],  # 单个样本
    X_test.columns,
    show=False,
    feature_order="importance",  # 按特征重要性排序
   
)
plt.title("单个样本的SHAP决策图", fontsize=12)
plt.show()

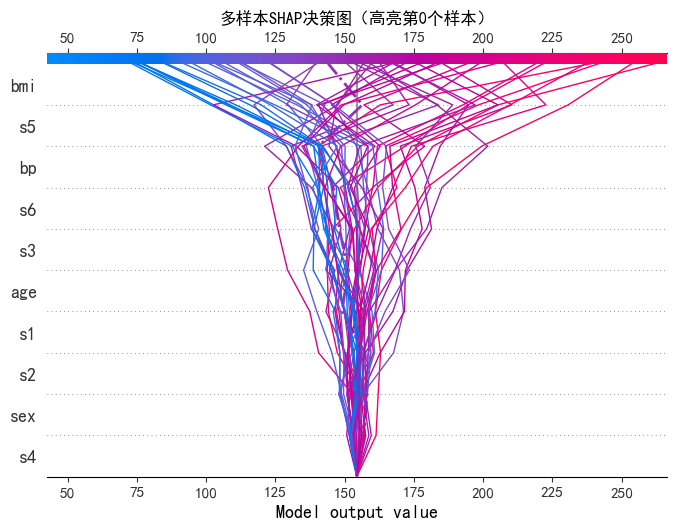
# 4.2 多个样本的决策图（前50个样本）
print("--- SHAP决策图（前50个样本） ---")
shap.decision_plot(
    base_value,
    shap_values[:50],  # 前50个样本
    X_test.columns,
    show=False,
    feature_order="importance",
    highlight=0  # 高亮第0个样本（红色）
)
plt.title("多样本SHAP决策图（高亮第0个样本）", fontsize=12)
plt.show()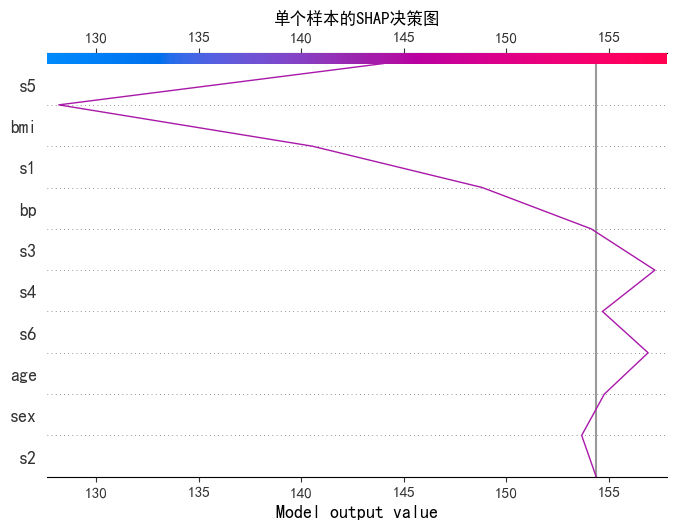

三、总结

分类任务与回归任务的区别

勇闯python的第32天@浙大疏锦行