28 Recommender System
28.1 Making Recommendations
接下来介绍推荐系统,以电影推荐为例
记有nun_unu个用户,nmn_mnm个电影,用户对这些电影有些有评分,而有些没有评分,用r(i,j)=1r(i, j) = 1r(i,j)=1表示用户j对第i个电影有评分
一种可行的推荐策略即预测用户没有评分的电影,如果预测用户会评高分,则推荐,反之不推荐
28.2 Using Per-item Features 使用每一项特征
除了用户对电影的评分,电影本身也有一些特征,例如爱情片的程度/动作片的程度等特征,现在先假定我们已知这些特征的值
记nnn表示电影的特征数量,每个特征为x(i)x^{(i)}x(i)
我们可以对每个用户建模一个线性回归模型,对于用户j有参数w(j),b(j)w^{(j)}, b^{(j)}w(j),b(j),那么用户j对电影i的评分预测值为w(j)x(i)+b(j)w^{(j)}x^{(i)}+b^{(j)}w(j)x(i)+b(j)
为了拟合参数,我们需要定义成本函数,记m(j)m^{(j)}m(j)表示用户j有评分的电影的数量,y(i,j)y^{(i, j)}y(i,j)表示用户j对电影i的评分,那么:
J(w(j),b(j))=12m(j)∑i:r(i,j)=1(w(j)x(i)+b(j)−y(i,j))2+λ2m(j)∑k=1n(wk(j))2J(w^{(j)}, b^{(j)}) = \frac 1 {2m^{(j)}} \sum_{i:r(i, j)=1} (w^{(j)}x^{(i)}+b^{(j)} - y^{(i, j)})^2 + \frac \lambda {2m^{(j)}} \sum_{k=1}^n (w_k^{(j)})^2J(w(j),b(j))=2m(j)1i:r(i,j)=1∑(w(j)x(i)+b(j)−y(i,j))2+2m(j)λk=1∑n(wk(j))2
对于推荐系统而言,这里的m(j)m^{(j)}m(j)作为常数通常可以不考虑:
J(w(j),b(j))=12∑i:r(i,j)=1(w(j)x(i)+b(j)−y(i,j))2+λ2∑k=1n(wk(j))2J(w^{(j)}, b^{(j)}) = \frac 1 {2} \sum_{i:r(i, j)=1} (w^{(j)}x^{(i)}+b^{(j)} - y^{(i, j)})^2 + \frac \lambda {2} \sum_{k=1}^n (w_k^{(j)})^2J(w(j),b(j))=21i:r(i,j)=1∑(w(j)x(i)+b(j)−y(i,j))2+2λk=1∑n(wk(j))2
目前分析的是单个用户的,考虑所有的nun_unu个用户:
J(w(1),...,w(nu)b(1),...,b(nu))=12∑jnu∑i:r(i,j)=1(w(j)x(i)+b(j)−y(i,j))2+λ2∑jnu∑k=1n(wk(j))2J\left( \begin{array}{c} w^{(1)}, ..., w^{(n_{u})} \\ b^{(1)}, ..., b^{(n_{u})} \end{array} \right) = \frac 1 {2} \sum_j^{n_u} \sum_{i:r(i, j)=1} (w^{(j)}x^{(i)}+b^{(j)} - y^{(i, j)})^2 + \frac \lambda {2} \sum_j^{n_u} \sum_{k=1}^n (w_k^{(j)})^2J(w(1),...,w(nu)b(1),...,b(nu))=21j∑nui:r(i,j)=1∑(w(j)x(i)+b(j)−y(i,j))2+2λj∑nuk=1∑n(wk(j))2
用梯度下降或其他优化方法,一起训练,可以得到一组效果不错的参数
但前提是我们已知这些特征的值,接下来讨论特征值未知时的做法
28.3 Collaborative Filtering Algorithm 协同过滤算法
我们现在有大量用户对电影的评分,可以基于这些用户评分去预测电影的特征
先假设已知 w(1),b(1),...,w(nu),b(nu)w^{(1)}, b^{(1)}, ..., w^{(n_{u})}, b^{(n_{u})}w(1),b(1),...,w(nu),b(nu),现在去预测x(i)x^{(i)}x(i)
J(x(i))=12∑j:r(i,j)=1(w(j)x(i)+b(j)−y(i,j))2+λ2∑k=1n(xk(i))2J(x^{(i)}) = \frac 1 {2} \sum_{j:r(i, j)=1} (w^{(j)}x^{(i)}+b^{(j)} - y^{(i, j)})^2 + \frac \lambda {2} \sum_{k=1}^n (x_k^{(i)})^2J(x(i))=21j:r(i,j)=1∑(w(j)x(i)+b(j)−y(i,j))2+2λk=1∑n(xk(i))2
对于所有的特征:
J(x(1),...,x(nm))=12∑i=1nm∑j:r(i,j)=1(w(j)x(i)+b(j)−y(i,j))2+λ2∑i=1nm∑k=1n(xk(i))2J(x^{(1)}, ..., x^{(n_m)}) = \frac 1 {2} \sum_{i=1}^{n_m} \sum_{j:r(i, j)=1} (w^{(j)}x^{(i)}+b^{(j)} - y^{(i, j)})^2 + \frac \lambda {2} \sum_{i=1}^{n_m} \sum_{k=1}^n (x_k^{(i)})^2J(x(1),...,x(nm))=21i=1∑nmj:r(i,j)=1∑(w(j)x(i)+b(j)−y(i,j))2+2λi=1∑nmk=1∑n(xk(i))2
之后是协同过滤算法的关键,把上式与28.2中分析的式子一起考虑,可以发现左边的累加项其实是一样的,都是对所有有用户评分的电影累加计算,那么我们可以合并两个式子,得到最终的成本函数:
J(w,b,x)=12∑(i,j):r(i,j)=1(w(j)x(i)+b(j)−y(i,j))2+λ2∑jnu∑k=1n(wk(j))2+λ2∑i=1nm∑k=1n(xk(i))2J(w, b, x) = \frac 1 {2} \sum_{(i, j):r(i, j)=1} (w^{(j)}x^{(i)}+b^{(j)} - y^{(i, j)})^2 + \frac \lambda {2} \sum_j^{n_u} \sum_{k=1}^n (w_k^{(j)})^2 + \frac \lambda {2} \sum_{i=1}^{n_m} \sum_{k=1}^n (x_k^{(i)})^2J(w,b,x)=21(i,j):r(i,j)=1∑(w(j)x(i)+b(j)−y(i,j))2+2λj∑nuk=1∑n(wk(j))2+2λi=1∑nmk=1∑n(xk(i))2
接下来应用优化方法最小化这个成本函数即可,例如梯度下降
28.4 Binary Labels 二元标签
在实际应用场景中,很多时候用户的反馈是二元的,例如对某个短视频喜欢或不喜欢
我们可以将算法推广到二元标签的情况,与线性回归推广到逻辑回归非常相似,我们预测用户打1的概率,即y(i,j)=1y(i, j)=1y(i,j)=1的概率,为g(z)=11+e−zg(z) = \frac 1 {1 + e^{-z}}g(z)=1+e−z1,其中z=w(j)x(i)+b(j)z = w^{(j)}x^{(i)}+b^{(j)}z=w(j)x(i)+b(j)
我们也类似地,用二元交叉熵损失函数代替平方误差损失函数:
L(f(w,b,x)(x),y(i,j))=−y(i,j)log(f(w,b,x)(x))−(1−y(i,j))log(1−f(w,b,x)(x))L(f_{(w, b, x)}(x), y^{(i, j)}) = -y^{(i, j)}log(f_{(w, b, x)}(x)) - (1 - y^{(i, j)})log(1 - f_{(w, b, x)}(x))L(f(w,b,x)(x),y(i,j))=−y(i,j)log(f(w,b,x)(x))−(1−y(i,j))log(1−f(w,b,x)(x))
其中的f是简记:
f(w,b,,x)(x)=g(w(j)x(i)+b(j))f_{(w, b, ,x)}(x) = g(w^{(j)}x^{(i)}+b^{(j)})f(w,b,,x)(x)=g(w(j)x(i)+b(j))
那么,成本函数为:
J(w,b,x)=∑(i,j):r(i,j)=1L(f(w,b,x)(x),y(i,j))J(w, b, x) = \sum_{(i, j):r(i, j)=1}L(f_{(w, b, x)}(x), y^{(i, j)})J(w,b,x)=(i,j):r(i,j)=1∑L(f(w,b,x)(x),y(i,j))
29 Recommender Systems Implementation
29.1 Mean Normalization 均值归一化
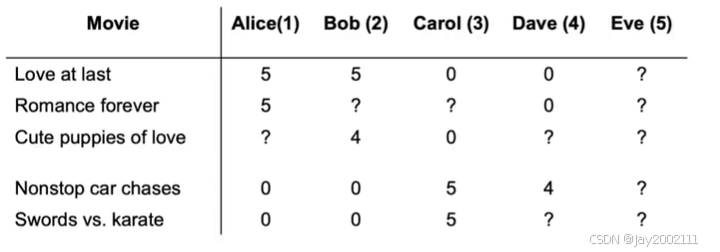
如上图,考虑这样一个问题,如果某一个新用户,对于任何电影都没有评分,那么直接用之前的协同过滤算法,这个新用户的参数w和b都将是0,因为成本函数的损失项不包括该新用户的w和b,所以为了让成本函数变小,正则化项里的w将会直接取0,b也很可能会取0(如果b初始化为0的话)
但是这不合理,我们应该将新用户的参数置为其他用户的参数均值更合理
所以均值归一化,就是将每个数减去行或列的均值
在本例中,针对没有评分的新用户,用"行归一化"更好,如果是针对没有评分的电影,用"列归一化"更好。但是这种情况下,用"行归一化"更好,因为没有评分的新用户比没有评分的电影更重要
注:均值归一化也能让算法运行地更快,但是最重要的是效果的改善
29.2 TensorFlow Implementation
之前我们介绍了TensorFlow实现神经网络,先构建网络架构,编译,训练,再推理
但是协同过滤不适用于这种框架,但是TensorFlow提供的工具仍然可以帮助我们用另一种方式实现协同过滤算法
为了实现梯度下降,我们需要得到成本函数的偏导,之前介绍的方法都是我们人工推导的,TensorFlow提供了一种工具可以方便地算出成本函数的偏导(即自动微分 Automatic Differentiation),叫做"梯度带"(Gradient Tape),示例:
python
# 以 J = (wx-1)^2为例, 即f(x)=wx, y = 1
w = tf.Variable(3.0) # tf.Variable表示我们想优化的参数,初始化值为3
x = 1.0
y = 1.0
alpha = 0.01
iterations = 30
for iter in range(iterations):
# 使用梯度带自动计算微分
with tf.GradientTape() as tape:
fwb = w * x
costJ = (fwb - y) ** 2
# 传入要求梯度的参数列表
[dJdw] = tape.gradient(costJ, [w])
# tf变量的运算需要特殊处理
w.assign_add(-alpha * dJdw)实际上,我们有了自动微分工具之后,不必采用梯度下降,可以用Adam优化器等其他优化方法:
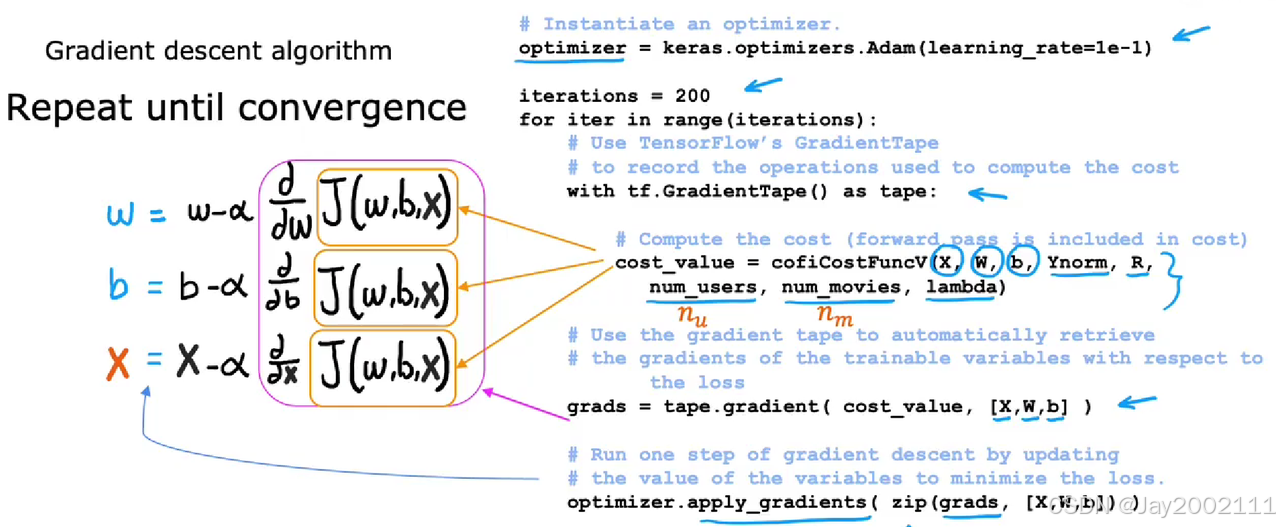
29.3 Finding Related Items
推荐系统的一个常见需求是,向用户推荐类似的事物
前面我们已经用协同过滤算法得出了每个事物的特征x,我们可以计算向量距离,取top-k个,即最相关的事物:
∥x(k)−x(i)∥2=∑l=1n(xl(k)−xl(i))2\|x^{(k)} - x^{(i)}\|^2 = \sum_{l=1}^n (x_l^{(k)} - x_l^{(i)})^2∥x(k)−x(i)∥2=l=1∑n(xl(k)−xl(i))2
最后,再说一下协同过滤算法的局限性:
- 冷启动问题处理不佳:仍然说的是对于几乎没有评分的用户,或几乎没有评分的电影,协同过滤算法表现不佳,虽然均值归一化可以解决一部分问题,但是存在更好的算法可以解决这个问题
- 没有使用已知的自然的事物的特征:例如用户的年龄、区域等特征,电影的参演演员、拍摄地点等特征,没有很好地利用上