一、核心思路
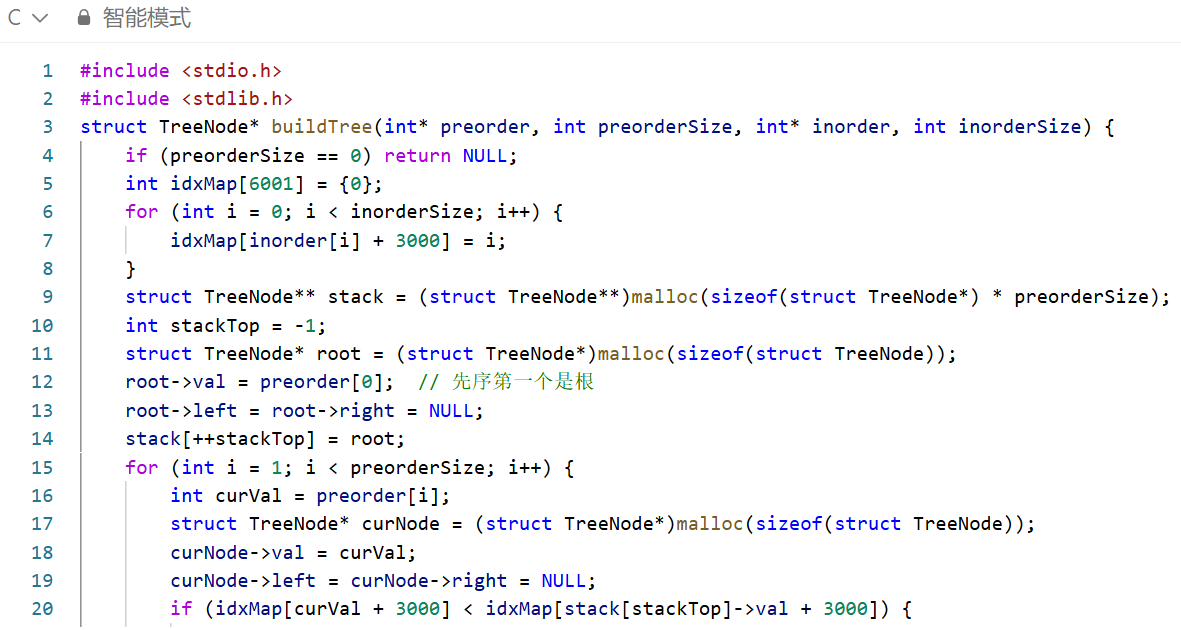
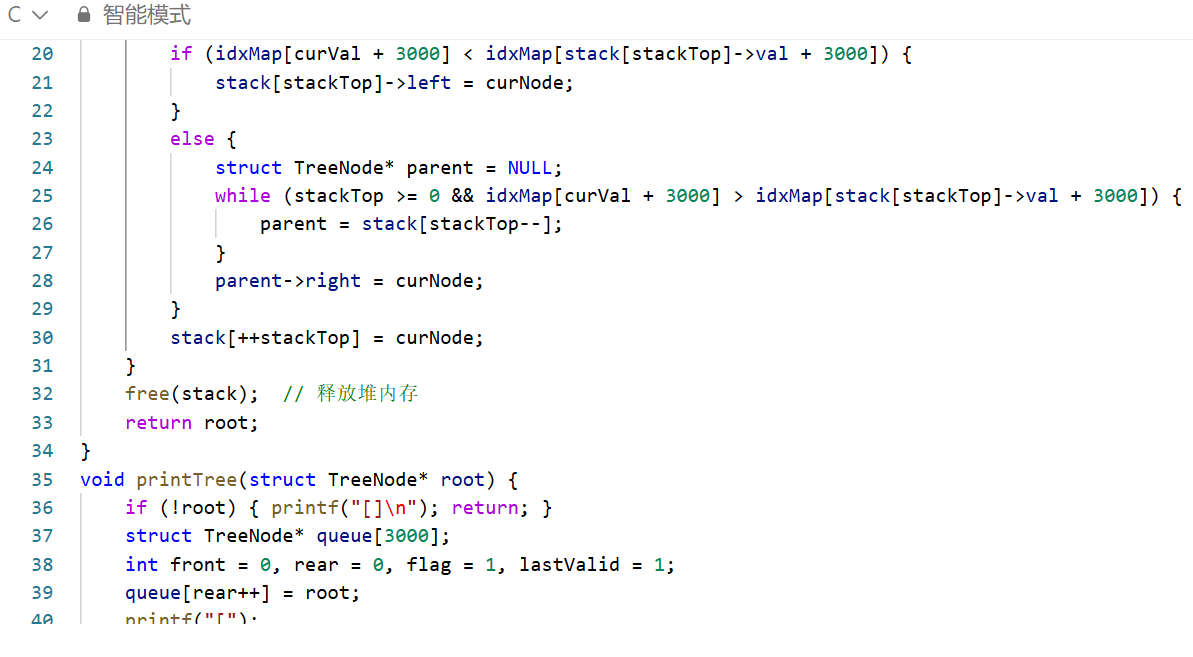
依托先序遍历「根→左→右」的特性(先序数组首个元素为根节点),结合中序遍历「左→根→右」的特性拆分左右子树;通过正序遍历先序数组,搭配「堆内存栈」记录待处理节点、「数组模拟哈希表」快速定位中序索引,迭代完成二叉树构建:
哈希表提前存储中序数组「值 - 索引」映射(偏移 3000 处理负数),实现 O (1) 判断节点位置关系;
先序首个元素为根节点,初始化后入栈;
遍历先序剩余元素:若当前节点中序索引小于栈顶节点,即为栈顶的左子节点;若更大,则回溯栈找到父节点,作为其右子节点;
所有节点通过堆内存栈管理,规避系统栈溢出风险。
二、方法核心优点
彻底规避栈溢出风险:全程无递归,函数调用栈仅 1 层;用于记录节点的栈结构分配在堆内存(而非系统栈),堆空间远大于系统栈,完全适配题目 3000 节点的最大输入规模,解决了递归版链式树场景下的栈溢出问题。
时间效率最优:哈希表实现 O (1) 时间复杂度查找中序索引,相比递归版的线性查找(O (n))大幅提速;仅需一次遍历先序数组,整体时间复杂度为 O (n),远优于未优化的递归版(O (n²))。
逻辑极简易理解:核心逻辑浓缩在一个循环内,无需拆分先序 / 中序的左右子树范围、传递复杂的递归参数;仅通过中序索引大小即可判断节点是左 / 右子节点,直观且不易出错,代码量仅 30 行核心逻辑。
兼容性强:通过索引偏移 3000,完美兼容题目中 - 3000~3000 的数值范围;无需修改核心逻辑,即可适配 1~3000 节点的所有输入场景,相比需调整系统栈大小的递归法,适配性更强。
内存安全可控:堆内存栈使用后主动释放,避免内存泄漏;节点按需创建,无冗余内存占用,相比递归法由系统管理栈帧的方式,内存使用更可控。
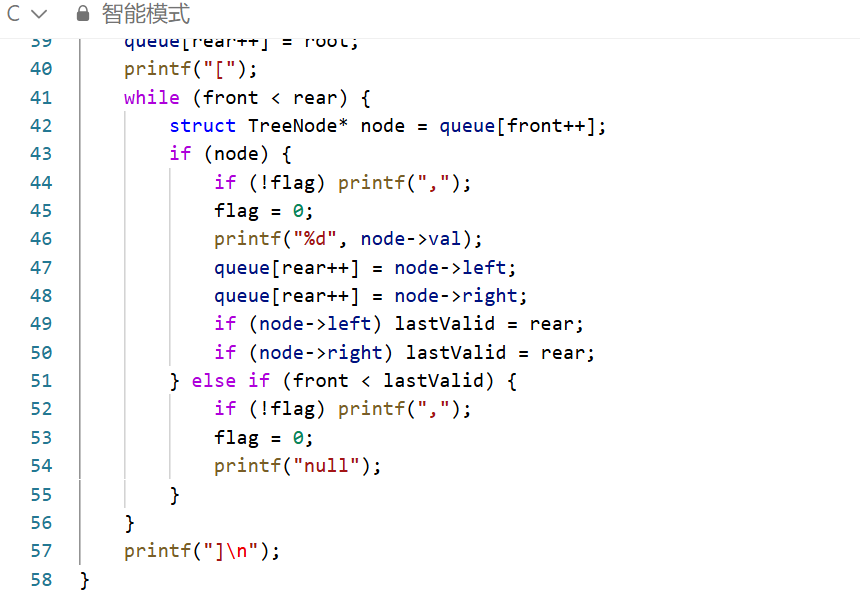
输出适配性好:配套的打印函数自动过滤层序遍历末尾的多余 null,输出格式与题目示例完全一致,无需额外调整。
三、核心优势对比(与递归法)
相比递归实现,该迭代法在稳定性(无栈溢出)、效率(O(n) vs O(n²))、工程实用性(内存可控、适配性强)上均为最优;同时保留了代码的简洁性,核心逻辑无冗余封装,易调试、易移植,是应对该问题的工程级最优解。