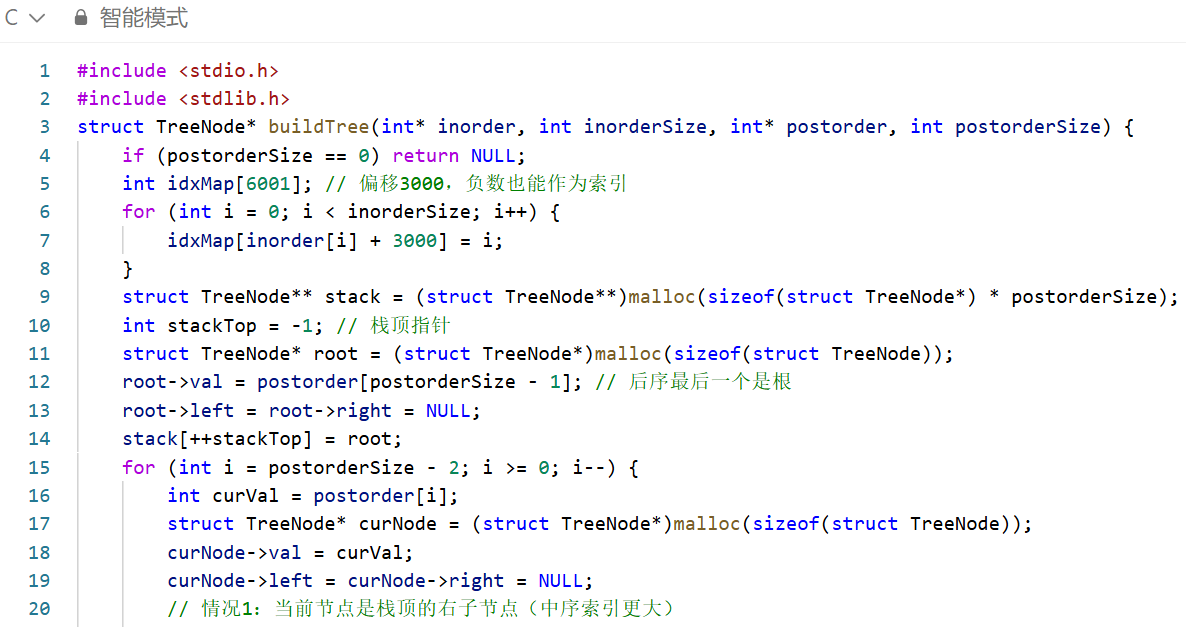
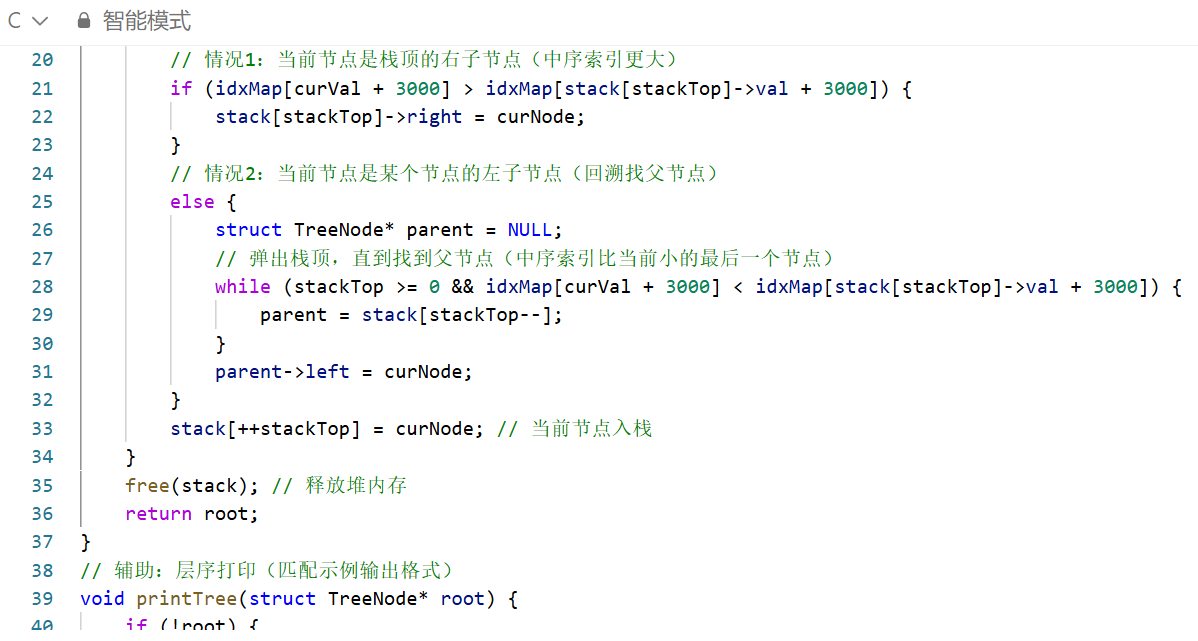
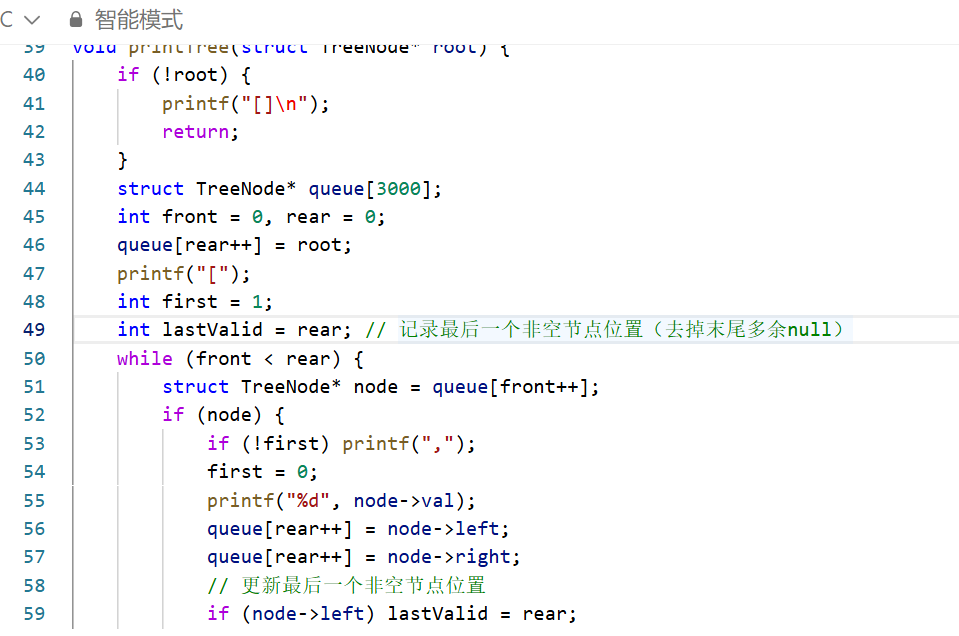
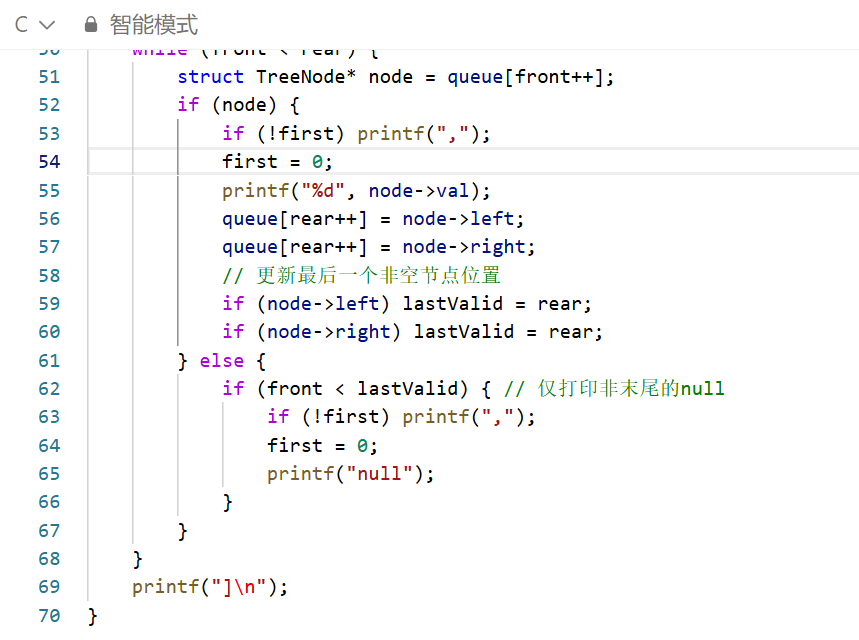
一、核心思路
基于后序遍历「左→右→根」的特性,后序数组最后一个元素是整棵树的根节点;结合中序遍历「左→根→右」的特性,可通过节点在中序数组中的索引判断左右子树归属。
具体实现时,反向遍历后序数组(遍历顺序为「根→右→左」),用栈记录待处理的节点,通过哈希表快速定位节点在中序数组的索引:若当前节点索引大于栈顶节点索引,说明是栈顶的右子节点;若更小,则回溯栈找到父节点,作为父节点的左子节点,最终迭代完成整棵树的构建。
二、方法核心优点
-
无栈溢出风险:全程采用迭代逻辑,函数调用栈仅一层,避免了递归法因节点数过多(如3000层链式树)导致的系统栈溢出问题;同时用于记录节点的栈结构分配在堆内存中,堆空间远大于系统栈,完全适配题目节点数上限。
-
时间效率高:通过数组模拟哈希表(偏移3000处理负数),实现O(1)时间复杂度查找节点在中序数组的索引,相比递归法的线性查找大幅提升效率;整体仅需一次遍历后序数组,时间复杂度为O(n),远优于未优化的递归法(O(n²))。
-
逻辑简洁易理解:核心逻辑集中在一个循环内,无需拆分左右子树范围、传递复杂的递归参数,仅通过中序索引大小即可判断节点的父子关系,直观且不易出错。
-
内存安全可控:堆内存分配的栈结构用完后可主动释放,避免内存泄漏;节点按需创建,无冗余内存占用,相比递归法由系统管理栈帧的方式,内存使用更可控。
-
适配性强:通过索引偏移处理负数节点值,兼容题目中-3000~3000的数值范围;核心逻辑无需修改即可适配1~3000节点的所有输入场景,相比需要调整系统栈大小的递归法,适配性更强。
三、与先序+中序迭代法的核心关联
两种方法逻辑完全对称:仅根节点位置(先序首元素/后序尾元素)、遍历方向(先序正序/后序逆序)、子节点判断条件(左子节点索引更小/右子节点索引更大)不同,核心都是通过栈记录节点、哈希表快速定位索引,规避递归缺陷的同时保证高效性。