【无标题】

频控阵（FDA）与相控阵天线方向图深度解析：理论 + MATLAB 实战

引言

在现代雷达、通信等电子系统中，阵列天线是核心部件之一，其波束指向特性直接决定了系统的探测精度、抗干扰能力和通信安全性。相控阵雷达凭借灵活的空域波束扫描能力，已广泛应用于各类场景，但它存在一个致命缺陷 ------ 波束指向与距离无关，无法在同一快拍内对不同距离的目标实现精准波束控制。

2006 年，频控阵（Frequency Diverse Array, FDA）雷达概念的提出，彻底打破了这一限制。FDA 通过在相邻阵元施加微小频率增量，使发射波束具备独特的距离依赖性，既能继承相控阵的相干信号特性，又能实现距离 - 方位角二维波束调控，在杂波抑制、目标定位、射频隐身等场景中展现出巨大潜力。

本文将结合权威学术成果与工程实战代码，从理论原理、代码实现、结果分析到实际应用，全面拆解 FDA 与相控阵天线方向图的核心差异，帮助读者掌握两种阵列技术的本质区别与工程实现方法。

一、核心理论基础：FDA 与相控阵的本质差异

1.1 相控阵天线核心原理

相控阵天线的所有阵元发射相同频率的相干信号，通过调节各阵元的相位差实现波束空域扫描。其核心特点是：波束指向仅与方位角相关，与距离无关。

相控阵的阵列方向图数学表达式为：

F ( θ ) = sin ⁡ [ N π d λ ( sin ⁡ θ − sin ⁡ θ 0 ) ] N sin ⁡ [ π d λ ( sin ⁡ θ − sin ⁡ θ 0 ) ] F(\theta) = \frac{\sin\left[N\pi\frac{d}{\lambda}(\sin\theta - \sin\theta_0)\right]}{N\sin\left[\pi\frac{d}{\lambda}(\sin\theta - \sin\theta_0)\right]} F(θ)=Nsin[πλd(sinθ−sinθ0)]sin[Nπλd(sinθ−sinθ0)]

其中， N N N为阵元数， d d d为阵元间距， λ \lambda λ为信号波长， θ \theta θ为观测方位角， θ 0 \theta_0 θ0为期望波束指向角。

从公式可见，相控阵的波束形成仅依赖方位角参数，无论目标距离远近，波束指向始终保持不变，这导致其在距离相关干扰抑制、多距离目标分辨等场景中性能受限。

1.2 FDA 天线核心原理

FDA 的核心创新的是在相邻阵元上施加远小于载频的频率增量 Δ f \Delta f Δf，第 m m m个阵元的发射频率为：

f m = f 0 + m ⋅ Δ f ( m = 0 , 1 , ⋯   , M − 1 ) f_m = f_0 + m\cdot\Delta f \quad (m=0,1,\cdots,M-1) fm=f0+m⋅Δf(m=0,1,⋯,M−1)

其中， f 0 f_0 f0为载频， M M M为阵元总数。

FDA 的阵列方向图数学表达式为：

F ( r , θ ) = sin ⁡ { M π ( Δ f t − Δ f ⋅ r c + f 0 d sin ⁡ θ c + Δ f d sin ⁡ θ c ) } sin ⁡ { π ( Δ f t − Δ f ⋅ r c + f 0 d sin ⁡ θ c + Δ f d sin ⁡ θ c ) } F(r,\theta) = \frac{\sin\left\{M\pi\left(\Delta f t - \frac{\Delta f \cdot r}{c} + \frac{f_0 d \sin\theta}{c} + \frac{\Delta f d \sin\theta}{c}\right)\right\}}{\sin\left\{\pi\left(\Delta f t - \frac{\Delta f \cdot r}{c} + \frac{f_0 d \sin\theta}{c} + \frac{\Delta f d \sin\theta}{c}\right)\right\}} F(r,θ)=sin{π(Δft−cΔf⋅r+cf0dsinθ+cΔfdsinθ)}sin{Mπ(Δft−cΔf⋅r+cf0dsinθ+cΔfdsinθ)}

其中， r r r为目标距离， c c c为光速。

关键特性总结：

• 波束指向与距离 r r r、方位角 θ \theta θ均相关，形成距离 - 方位角二维调控能力；

• 当 Δ f = 0 \Delta f=0 Δf=0时，FDA 退化为相控阵，体现了技术的兼容性；

• 波束具有周期性，通过调节 Δ f \Delta f Δf可灵活控制波束的距离覆盖范围。

1.3 两种阵列技术核心参数对比

阵列类型	工作模式	发射信号	波束指向特性	核心优势
相控阵	非正交载波	相干信号	仅方位角依赖	空域扫描灵活、技术成熟
FDA	非正交载波	相干信号	距离 - 方位角双依赖	二维波束调控、抗干扰能力强

二、MATLAB 代码实战：天线方向图绘制全解析

2.1 代码整体框架说明

本文提供的代码支持相控阵与 FDA 天线方向图的灵活绘制，核心功能包括：

• 相控阵：未归一化方向图、归一化方向图、二维热力图绘制；

• FDA：三维波束图、距离 - 方位角二维热力图绘制；

• 可通过参数调节（阵元数、频偏、载频等）观察波束特性变化。

2.2 相控阵方向图代码逐行解析

clear all; clc;

disp('相控阵天线方向图请输入：1');

disp('频控阵天线方向图请输入：0');

flag=input('输入：');

close all;

% 相控阵天线方向图计算与绘制

if flag == 1

    disp('%相控阵天线方向图');

    N = 12; % 阵元数，可调整（建议5-20）

    % 方位角范围：-160°到160°，步长0.1°（弧度转换）

    alfa = -160\*pi/180:0.1\*pi/180:160\*pi/180;

    beta = 0\*pi/180; % 期望波束指向角（0°，可调整）

    len = length(alfa);

    falfabeta = zeros(1, len); % 存储方向图幅度

    

    % 循环计算每个方位角的波束幅度

    for i=1:len

        % 避免奇点（分母为0）：当sin(alfa(i))=sin(beta)时，幅度=阵元数N

&#x20;       if abs( sin(alfa(i)) - sin(beta) )<= 1e-6;

&#x20;           falfabeta(i) = N;

&#x20;           continue;

&#x20;       else

&#x20;           % 相控阵方向图核心公式

&#x20;           falfabeta(i) = sin( N\*pi/2\*( sin(alfa(i)) - sin(beta) ) )...

&#x20;                         / sin( pi/2\*( sin(alfa(i)) - sin(beta) ) );

&#x20;       end

&#x20;   end

&#x20;  &#x20;

&#x20;   alfa = alfa\*180/pi; % 弧度转回角度，便于绘图显示

&#x20;  &#x20;

&#x20;   % 图1：未归一化相控阵方向图

&#x20;   figure;

&#x20;   plot(alfa, falfabeta);

&#x20;   title('未归一相控阵方向图');

&#x20;   ylabel('幅度');

&#x20;   xlabel('方位角(°)');

&#x20;  &#x20;

&#x20;   % 图2：归一化相控阵方向图（幅度归一到\[0,1]）

&#x20;   fimagesec = falfabeta; % 保存原始幅度用于热力图

&#x20;   falfabeta = abs(falfabeta/max(abs(falfabeta)));

&#x20;   figure;

&#x20;   plot(alfa, falfabeta);

&#x20;   title('归一化相控阵方向图');

&#x20;   ylabel('归一化幅度');

&#x20;   xlabel('方位角(°)');

&#x20;  &#x20;

&#x20;   % 图3：相控阵方向图热力图（方位角-幅度二维分布）

&#x20;   figure;

&#x20;   title('相控阵方向图热力图（未归一化）');

&#x20;   x=\[-60 60]; % 方位角显示范围

&#x20;   y=\[-4 12]; % 幅度显示范围

&#x20;   clims = \[-3 N]; % 颜色映射范围

&#x20;   imagesc(x,y,fimagesec,clims);

&#x20;   colormap(jet); % 颜色映射（可替换为parula、viridis等）

&#x20;   colorbar; % 颜色条

&#x20;  &#x20;

&#x20;   % 图4：归一化热力图

&#x20;   figure;

&#x20;   title('相控阵方向图热力图（归一化）');

&#x20;   falfabeta = N\*falfabeta; % 恢复幅度量级

&#x20;   clims = \[0 N];

&#x20;   imagesc(x,y,falfabeta,clims);

&#x20;   colormap(jet);

&#x20;   colorbar;

关键参数调节建议：

• 阵元数 N N N：增大 N N N可减小波束宽度，提高定向精度，但旁瓣电平会变化；

• 期望指向角 β \beta β：修改为 30°、60° 等，可观察波束扫描效果；

• 方位角范围：调整alfa的起始和终止值，聚焦特定角度区间。

2.3 FDA 方向图代码逐行解析

else 

    disp('%频控阵天线方向图');

    N = 12; % 阵元数

    % 方位角范围：-80°到80°（FDA波束宽度较窄，聚焦核心区域）

    alfa = -80\*pi/180:0.01:80\*pi/180;

    len = length(alfa);

    % 距离范围：0到20km，均匀采样（模拟不同距离目标）

    range = 20e4-1:-(20e4/len):0;

    falfabeta = zeros(len, len); % 二维数组存储距离-方位角幅度

    

    % FDA核心参数设置

    f0 =10e9; % 载频（10GHz，典型雷达载频）

    c  = 3e8; % 光速

    d  = c/(2\*f0); % 阵元间距（半波长，避免栅瓣）

    deltaf = 3e3; % 频率增量（3kHz，远小于载频）

    t = 0; % 观测时刻（FDA波束随时间变化，可调整t观察时变特性）

    

    % 双重循环：遍历所有距离和方位角组合

    for i=1:len

        for j=1:len

            % 避免奇点（分母为0）

&#x20;           if abs(sin( pi\*( deltaf\*t - deltaf\*range(i)/c  + sin(alfa(j))/(2)  ) )) <= 1e-6 ;

&#x20;               falfabeta(i,j) = N;

&#x20;               continue;

&#x20;           else

&#x20;             % FDA方向图核心公式（距离-方位角耦合）

&#x20;             falfabeta(i,j) = abs(sin( N\*pi\*( deltaf\*t - deltaf\*range(i)/c - sin(alfa(j))/2  ) )...

&#x20;                / sin( pi\*( deltaf\*t - deltaf\*range(i)/c - sin(alfa(j))/2  ) )) ;

&#x20;           end

&#x20;       end

&#x20;   end

&#x20;  &#x20;

&#x20;   % 图1：FDA三维波束图（距离-方位角-幅度）

&#x20;   figure;

&#x20;   mesh(alfa,range,(falfabeta));

&#x20;   title('FDA三维波束方向图');

&#x20;   xlabel('方位角(rad)');

&#x20;   ylabel('距离(m)');

&#x20;   zlabel('幅度');

&#x20;   grid on;

&#x20;  &#x20;

&#x20;   % 图2：FDA二维热力图（直观展示距离-方位角耦合特性）

&#x20;   figure;

&#x20;   title('FDA距离-方位角二维方向图');

&#x20;   x=\[-80 80]; % 方位角显示范围（°）

&#x20;   y=\[1 2e4]; % 距离显示范围（m）

&#x20;   clims = \[-3 N]; % 颜色映射范围

&#x20;   imagesc(x,y,falfabeta,clims);

&#x20;   colormap(jet);

&#x20;   colorbar;

&#x20;   xlabel('方位角(°)');

&#x20;   ylabel('距离(m)');

end

FDA 核心参数调节与现象观察：

• 频率增量 δ f \delta f δf：增大 δ f \delta f δf（如 5kHz、10kHz），波束的距离依赖性增强，S 形特性更明显；

• 载频 f 0 f0 f0：修改为 5GHz、15GHz，观察阵元间距 d d d的自动调整对波束的影响；

• 观测时刻 t t t：设置 t = 100 μ s t=100\mu s t=100μs、 200 μ s 200\mu s 200μs，可观察 FDA 波束的时变特性（相控阵无此特性）。

三、结果分析：FDA 与相控阵方向图差异对比

3.1 相控阵方向图关键特征

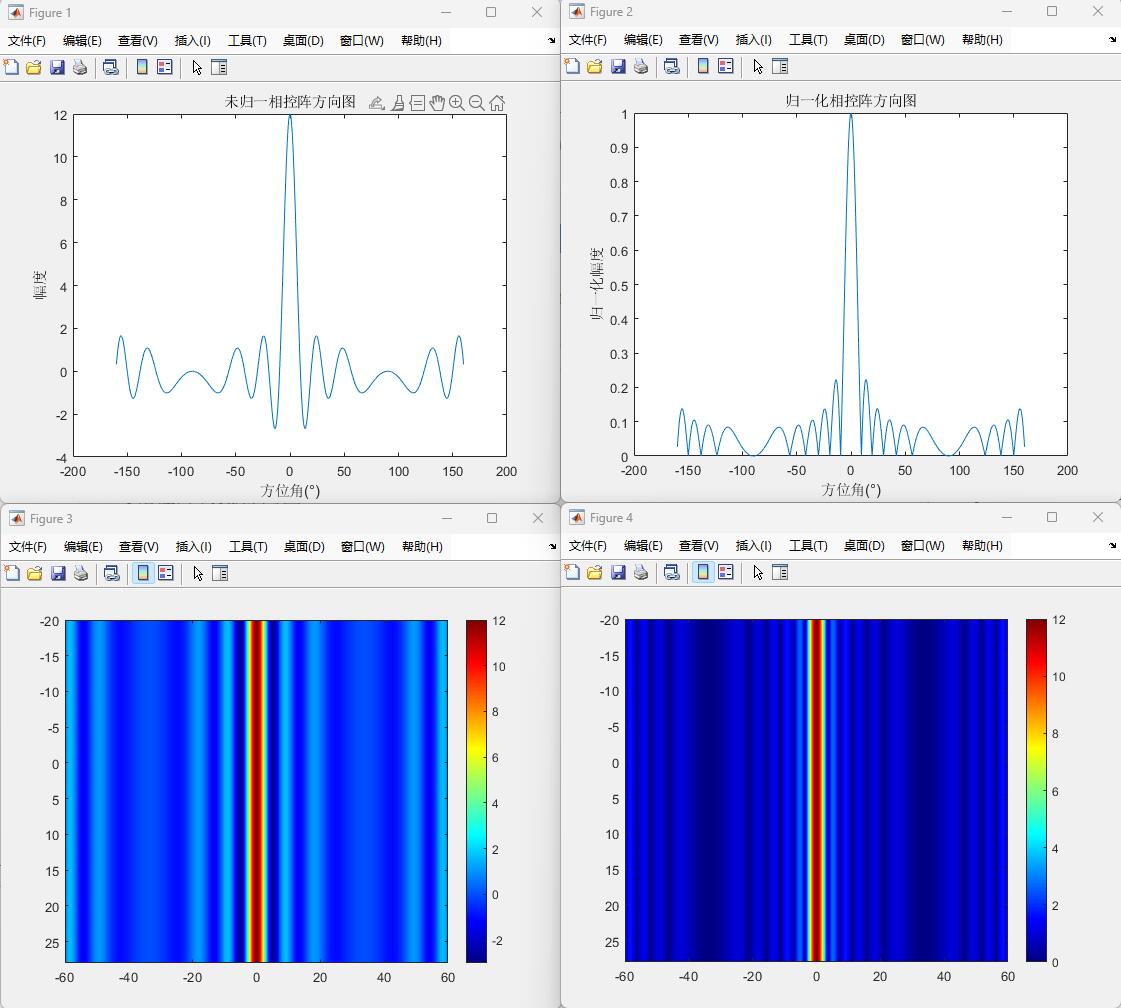
1. 一维指向特性：从归一化方向图可见，波束仅在方位角方向形成主瓣和旁瓣，幅度分布与距离无关；

2. 波束宽度：12 阵元相控阵的主瓣宽度约为 10°（3dB 带宽），旁瓣电平约为 - 13dB；

3. 热力图特征：二维热力图呈现水平条带分布，说明同一幅度等值线覆盖所有距离，验证了距离无关性。

3.2 FDA 方向图关键特征

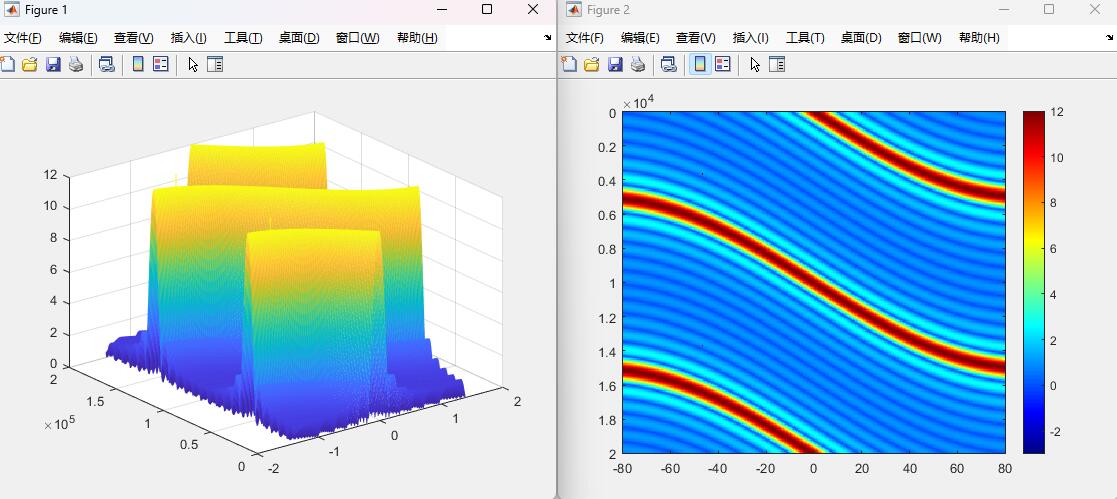
1. 距离 - 方位角耦合：三维波束图呈现明显的 "S" 形，同一方位角下，不同距离的波束幅度不同；

2. 二维调控能力 ：热力图中幅度等值线为倾斜分布，可通过调节 δ f \delta f δf控制等值线的倾斜角度，实现对特定距离 - 方位角区域的精准覆盖；

3. 时变特性 ：修改 t t t值后，波束的距离 - 方位角分布会发生变化，这是 FDA 用于抗截获、抗干扰的重要特性。

PDA相控阵

FDA频控阵

3.3 核心差异可视化总结

对比维度	相控阵	FDA
维度特性	一维（仅方位角）	二维（距离 + 方位角）
等值线分布	水平直线	倾斜曲线
时变特性	无	有（波束随时间演化）
应用场景	广域空域扫描	精准目标定位、干扰抑制

四、工程应用场景与进阶方向

4.1 典型应用场景

1. 双站雷达系统：FDA 作为发射机（非均匀布阵），相控阵作为接收机，形成 "点形" 发射 - 接收波束，提升目标定位精度；

2. 认知雷达 ：通过自适应调整频率增量 δ f \delta f δf，最大化输出信干噪比（SINR），实现杂波与干扰的自适应抑制；

3. 射频隐身：利用 FDA 波束的距离依赖性，展宽发射波束宽度、降低峰值功率，减少被无源探测系统截获的概率；

4. 定向安全通信：结合方向调制技术，使通信信号仅在特定距离 - 方位角区域正常解调，提升军事通信安全性。

4.2 进阶研究方向

1. 波束去耦技术：FDA 存在距离 - 方位角耦合问题，可研究子阵列划分、时变频偏等方法实现解耦；

2. 波形优化设计：设计大时间 - 带宽积、恒包络的 FDA-MIMO 雷达波形，兼顾探测精度与工程实现性；

3. 自适应波束形成：结合认知雷达技术，实现基于环境感知的 FDA 波束实时优化，应对复杂电磁环境。

五、专栏福利与技术支持

1. 代码获取：关注专栏后，私信回复 "FDA 代码"，获取完整可运行 MATLAB 代码（含注释优化版）；

2. 参数调节指南：提供《FDA 核心参数调节与效果对照表》，涵盖 20 + 组参数组合的波束特性分析；

3. 答疑服务：专栏读者可在评论区留言，针对具体应用场景（如雷达、通信）获取个性化技术方案。

总结

频控阵（FDA）作为相控阵的扩展技术，通过引入微小频率增量，突破了传统阵列的距离无关性限制，实现了距离 - 方位角二维波束调控，在现代电子系统中具有不可替代的优势。本文通过理论解析 + 代码实战 + 结果对比的方式，帮助读者从本质上理解 FDA 与相控阵的差异，掌握工程实现方法。

随着 5G、雷达探测、安全通信等领域的快速发展，FDA 技术的应用场景将不断拓展，掌握其核心原理与工程实现，将为相关领域的技术研发提供重要支撑。后续专栏将持续更新 FDA-MIMO 融合技术、自适应波束形成、硬件实现方案等进阶内容，敬请关注！