目录
[A. Channel](#A. Channel)
[B Split Sort](#B Split Sort)
[C. MEX Repetition](#C. MEX Repetition)
[D. Two-Colored Dominoes](#D. Two-Colored Dominoes)
引言:
今天我们来打Pinely Round 2 (Div. 1 + Div. 2)。
A. Channel
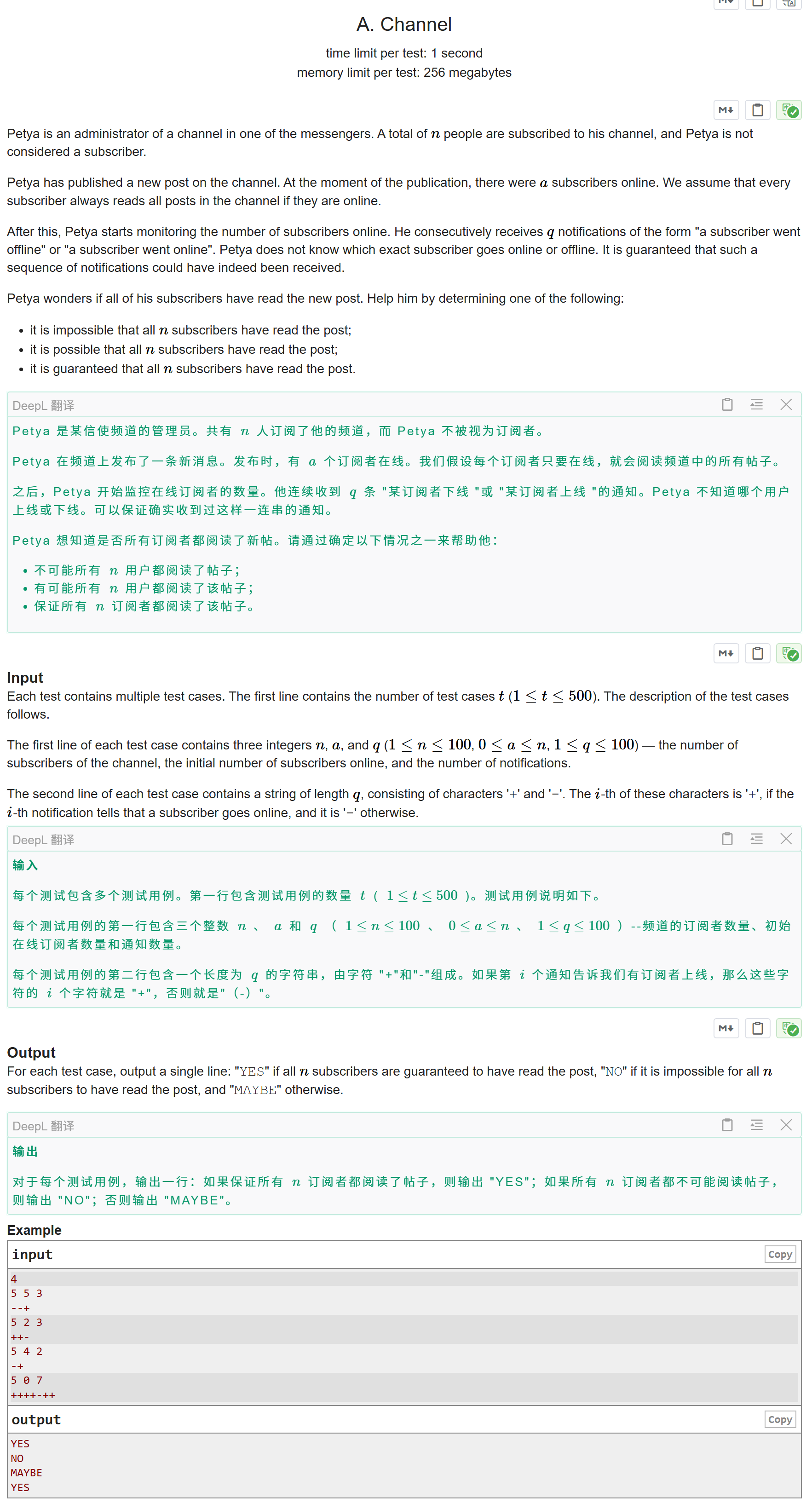
题目大意:
总共有 n 个人,最开始有 a 个人在线上,再给你 q 次消息,每次消息" + "表示上线," - "表示下线,每次上线都会读报,如果一定能够保证 n 个人都度过报输出YES,如果一定不能够保证 n 个人都度过报输出NO,剩下情况输出MAYBE.
算法分析:
只要同时在线的人数大于等于n就输出YES,如果 + 的数量加上原来在线的人数都不大于等于n,就输出NO,否则输出MAYBE
源码实现:
cpp
#include <iostream>
#include <string>
#include<numeric>
#include <map>
#include <vector>
#include <algorithm>
#include<unordered_set>
#include<unordered_map>
#include<cmath>
using namespace std;
typedef long long ll;
void solve()
{
int n, a, q;
cin >>n >> a >> q;
string s;
cin >> s;
int op = 0, oh = a;
int ans = a;
for (char c : s)
{
if (c == '+')
{
op++;
oh++;
ans = max(ans, oh);
}
else {
oh--;
}
}
if (ans >= n)
{
cout << "YES" << endl;
}
else if (a + op < n)
{
cout << "NO" << endl;
}
else {
cout << "MAYBE" << endl;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}B Split Sort
题目链接:B Split Sort
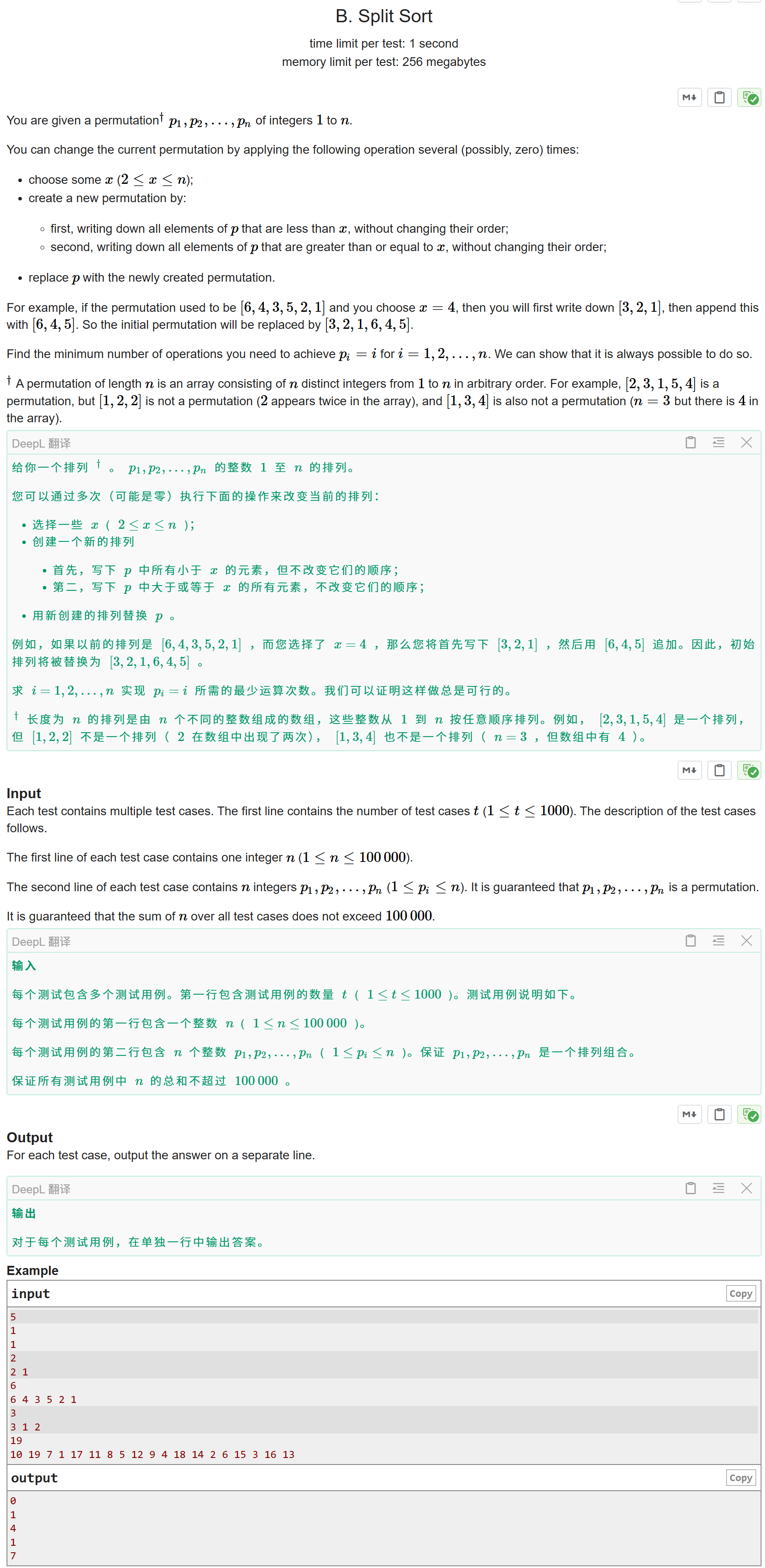
题目大意:
给一个n的排列,问最少通过几次以下操作,将这个排列还原为升序的,操作:选择一些 x (2<=x<=n),创建一个新的排列组合,首先,写下 p 中所有小于 x 的元素,但不改变它们的顺序;第二,写下 p 中大于或等于 x 的所有元素,但不改变它们的顺序,用新创建的排列替换p 。
算法分析:
通过找规律可以发现,6,5,4,3,2,1的还原步骤:选6->5,4,3,2,1,6,选5->4,3,2,1,5,6
选4->3,2,1,4,5,6,选3一2,1,3,4,5,6,选2->1,2,3,4,5,6需要5步,也就是说只要在给的排列中较大那个数的位置在较小那个数的为值的后面,就不用操作,二、我们最多只会操作n-1次,所以当我们遇见上面的情况的时候,就将操作次数减一就行
源码实现:
cpp
#include <iostream>
#include <string>
#include<numeric>
#include <map>
#include <vector>
#include <algorithm>
#include<unordered_set>
#include<unordered_map>
#include<cmath>
using namespace std;
typedef long long ll;
void solve()
{
int n;
cin >> n;
vector<int> a(n+1);
for (int i = 1; i <= n; i++)
{
int op;
cin >> op;
a[op] = i;
}
int ans = n-1 ;
for (int i = n; i > 1; i--)
{
if (a[i] > a[i - 1])
{
ans--;
}
}
cout << ans << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}C. MEX Repetition
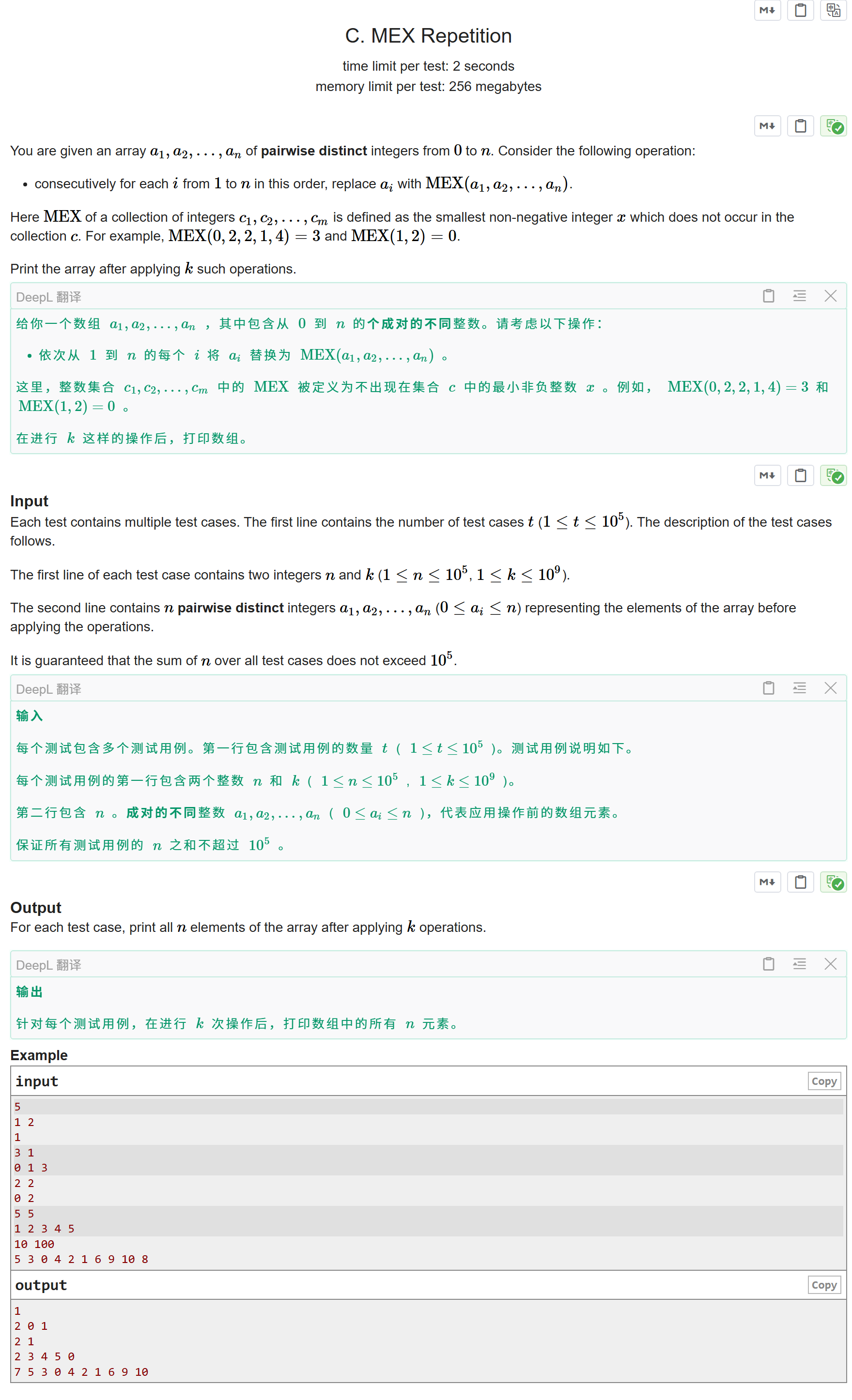
题目大意:
给你一个数组a1,a2,···,an,它是由0到n之间个成对的不同整数组成的。请考虑以下操作:依次将ai替换为MEX(a1,a2,··,an)问经过k次这样操作的数组会变成什么样,输出操作后的数组
算法分析:
找规律可以发现,经过n+1操作数组又变回原来的样子,所以这是以n+1为周期的循环,而且发现每次操作就是把最后一个数字删除,在数组的首加上MEX(a1,a2,···,an),其实这个值就是上一次被删了的数,所以总的复杂度是O(n),我直接就用vector做的,也可以用双端队列
源码实现:
cpp
#include <iostream>
#include <string>
#include<numeric>
#include <map>
#include <vector>
#include <algorithm>
#include<unordered_set>
#include<unordered_map>
#include<cmath>
using namespace std;
typedef long long ll;
void solve()
{
int n, k;
cin>> n >> k;
vector<int> a(n);
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
int ans = 0;
vector<int> b = a;
sort(b.begin(), b.end());
for (int i = 0; i < n; i++)
{
if (b[i] == ans)
ans++;
}
reverse(a.begin(), a.end());
int cnt = k % (n + 1); //(n+1)周期循坏
for (int i = 0; i < cnt; i++)
{
a.push_back(ans);
ans = a[i];
}
reverse(a.begin(), a.end());
for (int i = 0; i < n; i++)
{
cout << a[i] << " ";
}
cout << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}D. Two-Colored Dominoes
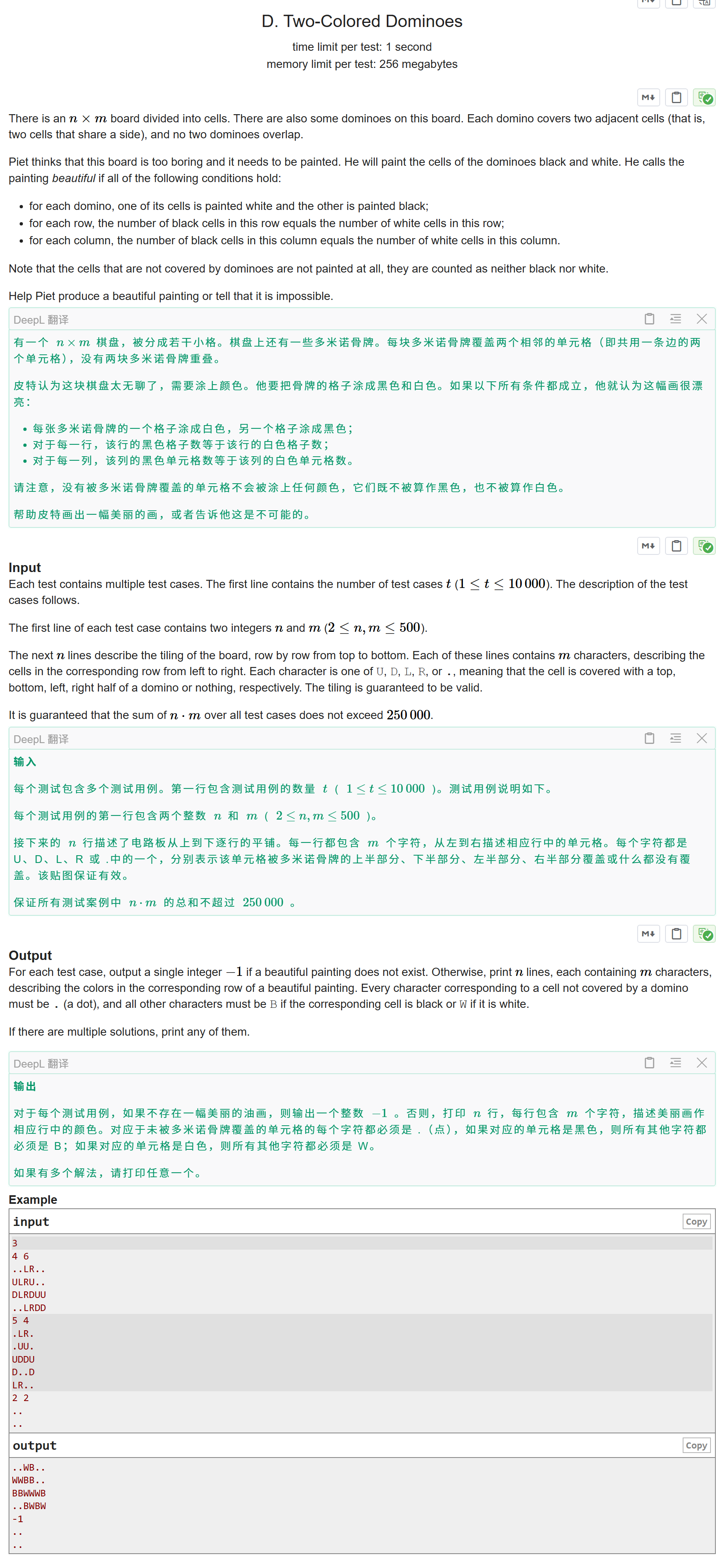
题目大意:
给一个由.LRUD组成的二维数组,问你能否把它在出.的地方图上白色或黑色,使得每一行并且每一列的白色和黑色相等,如果不行输出 -1。
算法分析:
我们发现,横着的多米诺骨牌,对每一行的白色和黑色数量关系没有影响,竖着的多米诺骨牌,对每一列的白色和黑色数量关系没有影响,所以,对于每一行我们只考虑竖着的(也就是UD),对于每一列我们只考虑横着的(也就是LR)
源码实现:
cpp
#include <iostream>
#include <string>
#include<numeric>
#include <map>
#include <vector>
#include <algorithm>
#include<unordered_set>
#include<unordered_map>
#include<cmath>
using namespace std;
typedef long long ll;
void solve() {
int n, m;
cin >> n >> m;
vector<vector<char>> a(n, vector<char>(m));
vector<vector<char>> b(n, vector<char>(m, '.'));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> a[i][j];
}
}
for (int i = 0; i < n; i++) {
int res = 0;
vector<int> ans;
for (int j = 0; j < m; j++) {
if (a[i][j] == 'U') {
res++;
ans.push_back(j);
}
}
if (res % 2 != 0) {
cout << -1 << endl;
return;
}
for (int j = 0; j < ans.size() / 2; j++)b[i][ans[j]] = 'B', b[i + 1][ans[j]] = 'W';
for (int j = ans.size() / 2; j < ans.size(); j++)b[i][ans[j]] = 'W', b[i + 1][ans[j]] = 'B';
}
for (int j = 0; j < m; j++) {
int res = 0;
vector<int> ans;
for (int i = 0; i < n; i++) {
if (a[i][j] == 'L') {
res++;
ans.push_back(i);
}
}
if (res % 2 != 0) {
cout << -1 << endl;
return;
}
for (int i = 0; i < ans.size() / 2; i++)b[ans[i]][j] = 'B', b[ans[i]][j + 1] = 'W';
for (int i = ans.size() / 2; i < ans.size(); i++)b[ans[i]][j] = 'W', b[ans[i]][j + 1] = 'B';
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cout << b[i][j];
}
cout << endl;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}结语:
以上就是四道题的题解,希望对你们有帮助,谢谢观看呀,如果有什么问题欢迎在评论区指出,我会继续努力哒!
