定积分的计算
基本考查
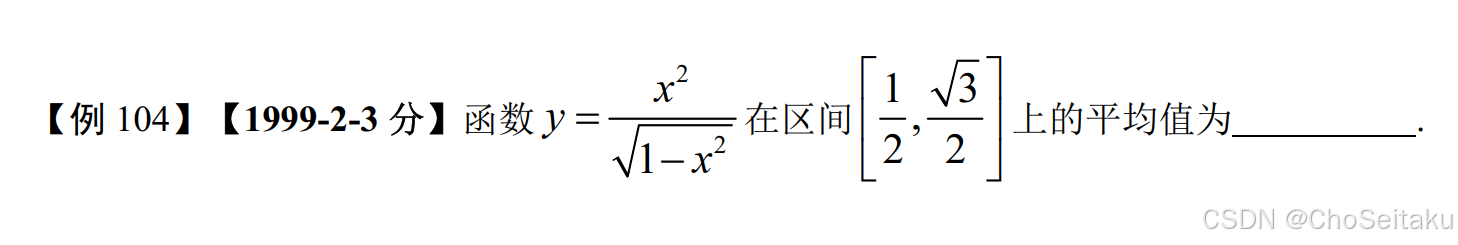
解:∫1232x21−x2dx32−12=x=sint23−1∫π6π3sin2tcost⋅costdt=(3+1)∫π6π31−cos2t2dt=(3+1)(12⋅π6−sin2t4∣π6π3)=π12(3+1) \begin{aligned} &\text{解:}\frac{\int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}} \frac{x^2}{\sqrt{1-x^2}}dx}{\frac{\sqrt{3}}{2} - \frac{1}{2}} \xlongequal{x=\sin t} \frac{2}{\sqrt{3}-1}\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{\sin^2 t}{\cos t} \cdot \cos t dt \\ &= (\sqrt{3}+1)\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{1-\cos 2t}{2}dt = (\sqrt{3}+1)\left( \frac{1}{2} \cdot \frac{\pi}{6} - \frac{\sin 2t}{4} \bigg|_{\frac{\pi}{6}}^{\frac{\pi}{3}} \right) \\ &= \frac{\pi}{12}(\sqrt{3}+1) \end{aligned} 解:23 −21∫2123 1−x2 x2dxx=sint 3 −12∫6π3πcostsin2t⋅costdt=(3 +1)∫6π3π21−cos2tdt=(3 +1)(21⋅6π−4sin2t 6π3π)=12π(3 +1)
【小结】积分平均值简称为平均值。 \boxed{【小结】}\text{积分平均值简称为平均值。} 【小结】积分平均值简称为平均值。
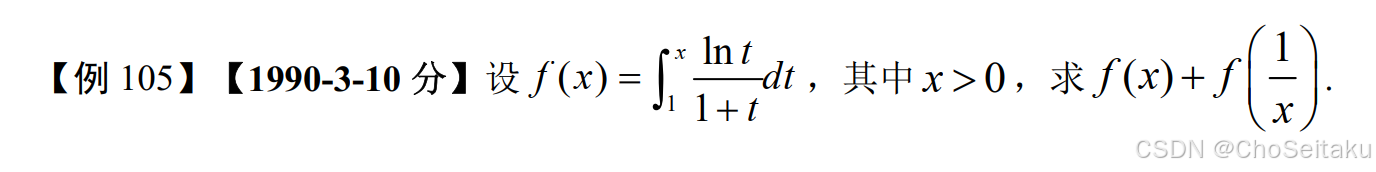
解:f(1x)=∫11xlnt1+tdt=u=1t∫1xln1u1+1ud(1u)=∫1x−lnu1+1u(−1u2)du=∫1xlnuu2+uduf(x)+f(1x)=∫1x(lnt1+t+lntt2+t)dt=∫1xlnttdt=12ln2x \begin{aligned} &\text{解:}f\left(\frac{1}{x}\right)=\int_{1}^{\frac{1}{x}} \frac{\ln t}{1+t}dt \xlongequal{u=\frac{1}{t}} \int_{1}^{x} \frac{\ln \frac{1}{u}}{1+\frac{1}{u}} d\left(\frac{1}{u}\right) = \int_{1}^{x} \frac{-\ln u}{1+\frac{1}{u}} \left(-\frac{1}{u^2}\right)du \\ &= \int_{1}^{x} \frac{\ln u}{u^2+u} du \\ \\ &f(x)+f\left(\frac{1}{x}\right)=\int_{1}^{x} \left( \frac{\ln t}{1+t} + \frac{\ln t}{t^2+t} \right)dt = \int_{1}^{x} \frac{\ln t}{t} dt = \frac{1}{2}\ln^2 x \end{aligned} 解:f(x1)=∫1x11+tlntdtu=t1 ∫1x1+u1lnu1d(u1)=∫1x1+u1−lnu(−u21)du=∫1xu2+ulnuduf(x)+f(x1)=∫1x(1+tlnt+t2+tlnt)dt=∫1xtlntdt=21ln2x
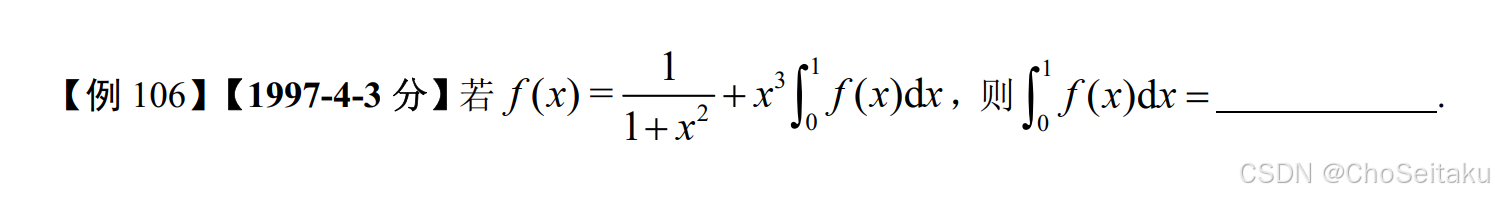
解:设∫01f(x)dx=A,两边同时在(0,1)上积分.∫01f(x)dx=∫0111+x2dx+∫01Ax3dxA=∫0111+x2dx+A∫01x3dxA=arctanx∣01+14A34A=π4 ⟹ A=π3 \begin{aligned} &\text{解:设}\int_{0}^{1}f(x)dx=A\text{,两边同时在}(0,1)\text{上积分.} \\ &\int_{0}^{1}f(x)dx = \int_{0}^{1}\frac{1}{1+x^2}dx + \int_{0}^{1}Ax^3dx \\ &A = \int_{0}^{1}\frac{1}{1+x^2}dx + A\int_{0}^{1}x^3dx \\ &A = \arctan x \bigg|_{0}^{1} + \frac{1}{4}A \\ &\frac{3}{4}A = \frac{\pi}{4} \implies A = \frac{\pi}{3} \end{aligned} 解:设∫01f(x)dx=A,两边同时在(0,1)上积分.∫01f(x)dx=∫011+x21dx+∫01Ax3dxA=∫011+x21dx+A∫01x3dxA=arctanx 01+41A43A=4π⟹A=3π
【小结】函数的解析式中如果出现定积分,则先将该定积分令成A,再代入计算。 \boxed{【小结】}\text{函数的解析式中如果出现定积分,则先将该定积分令成}A\text{,再代入计算。} 【小结】函数的解析式中如果出现定积分,则先将该定积分令成A,再代入计算。
分段函数的积分
- 显式分段函数

解:法1:F(x)=∫1xf(t)dt={∫1xtdt, 0≤x<1∫1x1dt, 1≤x≤2={x33−13, 0≤x<1x−1, 1≤x≤2 \begin{aligned} &\text{解:法1:}F(x)=\int_{1}^{x}f(t)dt= \begin{cases} \displaystyle \int_{1}^{x}t dt,\ &0\leq x<1 \\ \displaystyle \int_{1}^{x}1 dt,\ &1\leq x\leq2 \end{cases} = \begin{cases} \displaystyle \frac{x^3}{3} - \frac{1}{3},\ &0\leq x<1 \\ x - 1,\ &1\leq x\leq2 \end{cases} \end{aligned} 解:法1:F(x)=∫1xf(t)dt=⎩ ⎨ ⎧∫1xtdt, ∫1x1dt, 0≤x<11≤x≤2=⎩ ⎨ ⎧3x3−31, x−1, 0≤x<11≤x≤2
法2:F(1)=∫11f(t)dt=0,排除A;F(x)连续,排除C. 故选(D) \begin{aligned} &\text{法2:}F(1)=\int_{1}^{1}f(t)dt=0,\text{排除}A; \\ &F(x)\text{连续,排除}C.\ \text{故选}(D) \end{aligned} 法2:F(1)=∫11f(t)dt=0,排除A;F(x)连续,排除C. 故选(D)
【小结】1. 方法一直接分段计算在概率论中经常会考查,数一、三同学必须要掌握,但在高数中往往以选择题出现,学生面对选择题时应该要掌握方法二。2. 方法二是用两点进行判断:①变限积分一定能找到一个零点;②变限积分一定连续。 \begin{aligned} &\boxed{【小结】}1.\ \text{方法一直接分段计算在概率论中经常会考查,数一、三同学必须要掌握,但} \\ &\quad \text{在高数中往往以选择题出现,学生面对选择题时应该要掌握方法二。} \\ &2.\ \text{方法二是用两点进行判断:①变限积分一定能找到一个零点;②变限积分一定连续。} \end{aligned} 【小结】1. 方法一直接分段计算在概率论中经常会考查,数一、三同学必须要掌握,但在高数中往往以选择题出现,学生面对选择题时应该要掌握方法二。2. 方法二是用两点进行判断:①变限积分一定能找到一个零点;②变限积分一定连续。
- 隐式分段函数
(①符号sgn(x) ②绝对值. ③取整. ④最大值 ⑤最小值)思路:化为显式. \begin{aligned} &(\text{①符号}\text{sgn}(x)\ ②\text{绝对值. ③取整. ④最大值 ⑤最小值}) \\ &\text{思路:化为显式.} \end{aligned} (①符号sgn(x) ②绝对值. ③取整. ④最大值 ⑤最小值)思路:化为显式.

解:当−1≤x≤0时,−1≤t≤x≤0.∫−1x(1−∣t∣)dt=∫−1x(1+t)dt=[t+t22]−1x=(x+x22)−(−1+12)=12x2+x+12=12(x+1)2当x>0时∫−1x(1−∣t∣)dt=∫−10(1+t)dt+∫0x(1−t)dt=12+(x−x22)故f(x)={12+x−x22, x>012(x+1)2, −1≤x≤0 \begin{aligned} &\text{解:当}-1 \leq x \leq 0\text{时,}-1 \leq t \leq x \leq 0. \\ &\int_{-1}^{x} (1-|t|)dt = \int_{-1}^{x} (1+t)dt = \left[ t + \frac{t^2}{2} \right]{-1}^{x} = \left(x + \frac{x^2}{2}\right) - \left(-1 + \frac{1}{2}\right) = \frac{1}{2}x^2 + x + \frac{1}{2} = \frac{1}{2}(x+1)^2 \\ \\ &\text{当}x > 0\text{时} \\ &\int{-1}^{x} (1-|t|)dt = \int_{-1}^{0} (1+t)dt + \int_{0}^{x} (1-t)dt = \frac{1}{2} + \left( x - \frac{x^2}{2} \right) \\ \\ &\text{故}f(x)= \begin{cases} \displaystyle \frac{1}{2} + x - \frac{x^2}{2},\ &x > 0 \\ \displaystyle \frac{1}{2}(x+1)^2,\ &-1\leq x\leq 0 \end{cases} \end{aligned} 解:当−1≤x≤0时,−1≤t≤x≤0.∫−1x(1−∣t∣)dt=∫−1x(1+t)dt=[t+2t2]−1x=(x+2x2)−(−1+21)=21x2+x+21=21(x+1)2当x>0时∫−1x(1−∣t∣)dt=∫−10(1+t)dt+∫0x(1−t)dt=21+(x−2x2)故f(x)=⎩ ⎨ ⎧21+x−2x2, 21(x+1)2, x>0−1≤x≤0
【小结】被积函数中自变量要根据上下限范围讨论,把对应区间的解析式写出来,再求积分。 \boxed{【小结】}\text{被积函数中自变量要根据上下限范围讨论,把对应区间的解析式写出来,再求积分。} 【小结】被积函数中自变量要根据上下限范围讨论,把对应区间的解析式写出来,再求积分。
对称区间上的积分
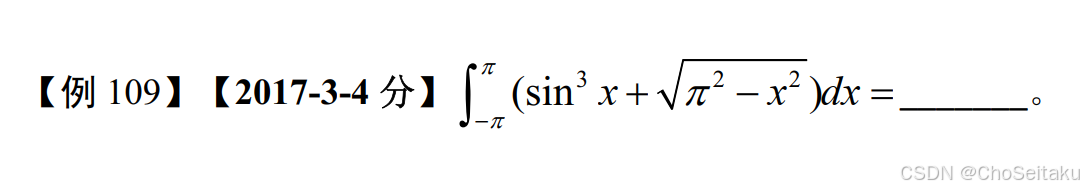
解:∫−ππsin3xdx=0∫−πππ2−x2dx=π2⋅π2 \begin{aligned} &\text{解:}\int_{-\pi}^{\pi}\sin^3 x dx = 0 \\ \\ &\int_{-\pi}^{\pi}\sqrt{\pi^2 - x^2} dx = \frac{\pi}{2} \cdot \pi^2 \end{aligned} 解:∫−ππsin3xdx=0∫−πππ2−x2 dx=2π⋅π2
【小结】1. 见到对称区间,优先考虑利用被积函数的奇偶性进行化简,即∫−aaf(x)dx={0,f(x)为奇函数2∫0af(x)dx,f(x)为偶函数。2. 有些特殊的积分可以考虑通过定义(算图像面积)解决。 \begin{aligned} &\boxed{【小结】}1.\ \text{见到对称区间,优先考虑利用被积函数的奇偶性进行化简,即} \\ &\quad \int_{-a}^{a} f(x)dx = \begin{cases} \displaystyle 0, & f(x)\text{为奇函数} \\ \displaystyle 2\int_{0}^{a} f(x)dx, & f(x)\text{为偶函数} \end{cases}。 \\ &2.\ \text{有些特殊的积分可以考虑通过定义(算图像面积)解决。} \end{aligned} 【小结】1. 见到对称区间,优先考虑利用被积函数的奇偶性进行化简,即∫−aaf(x)dx=⎩ ⎨ ⎧0,2∫0af(x)dx,f(x)为奇函数f(x)为偶函数。2. 有些特殊的积分可以考虑通过定义(算图像面积)解决。
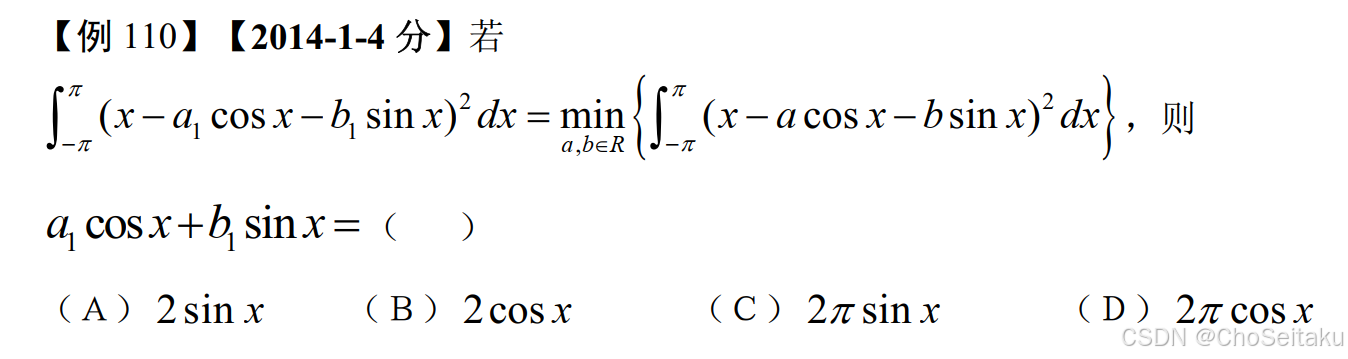
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc∫0πxsinxdx=π2∫0πsinxdx=π∫0πcos2xdx=2∫0π2cos2xdx=2⋅π4=π2解:∫−ππ(x2+a2cos2x+b2sin2x−2axcosx−2bxsinx+2absinxcosx)dx=2∫0πx2dx+2a2∫0πcos2xdx+2b2∫0πsin2xdx−4b∫0πxsinxdx=23π3+2a2⋅π2+2b2⋅π2−4b⋅π=23π3+πa2+π(b2−4b)当a=0, b=2时,取最小. a1cosx+b1sinx=2sinx, 选(A) \begin{aligned} &(a+b+c)^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc \\ \\ &\int_{0}^{\pi} x\sin x dx = \frac{\pi}{2}\int_{0}^{\pi}\sin x dx = \pi \\ \\ &\int_{0}^{\pi}\cos^2 x dx = 2\int_{0}^{\frac{\pi}{2}}\cos^2 x dx = 2 \cdot \frac{\pi}{4} = \frac{\pi}{2} \\ \\ &\text{解:}\int_{-\pi}^{\pi} \left(x^2 + a^2\cos^2 x + b^2\sin^2 x - 2ax\cos x - 2bx\sin x + 2ab\sin x\cos x\right) dx \\ &= 2\int_{0}^{\pi} x^2 dx + 2a^2\int_{0}^{\pi}\cos^2 x dx + 2b^2\int_{0}^{\pi}\sin^2 x dx - 4b\int_{0}^{\pi}x\sin x dx \\ &= \frac{2}{3}\pi^3 + 2a^2 \cdot \frac{\pi}{2} + 2b^2 \cdot \frac{\pi}{2} - 4b \cdot \pi = \frac{2}{3}\pi^3 + \pi a^2 + \pi(b^2 - 4b) \\ \\ &\text{当}a=0,\ b=2\text{时,取最小. }a_1\cos x + b_1\sin x = 2\sin x,\ \text{选}(A) \end{aligned} (a+b+c)2=a2+b2+c2+2ab+2ac+2bc∫0πxsinxdx=2π∫0πsinxdx=π∫0πcos2xdx=2∫02πcos2xdx=2⋅4π=2π解:∫−ππ(x2+a2cos2x+b2sin2x−2axcosx−2bxsinx+2absinxcosx)dx=2∫0πx2dx+2a2∫0πcos2xdx+2b2∫0πsin2xdx−4b∫0πxsinxdx=32π3+2a2⋅2π+2b2⋅2π−4b⋅π=32π3+πa2+π(b2−4b)当a=0, b=2时,取最小. a1cosx+b1sinx=2sinx, 选(A)
三角函数定积分.① ∫0π2sintdt=1, ∫0πsintdt=2, ∫π2πsintdt=1, ∫02πsintdt=0∫0π2sin2tdt=π4, ∫0πsin2tdt=2∫0π2sin2tdt=π2∫03π2sin2tdt=3∫0π2sin2tdt=3π4, ∫02πsin2tdt=4∫0π2sin2tdt=π∫0π2sin3tdt=23, ∫0πsin3tdt=2∫0π2sin3tdt=43∫03π2sin3tdt=23, ∫02πsin3tdt=0② ∫0π2costdt=1, ∫0πcostdt=0, ∫π2πcostdt=−1∫02πcostdt=0 \begin{aligned} &\text{三角函数定积分.} \\ \\ &①\ \int_{0}^{\frac{\pi}{2}}\sin t dt=1,\ \int_{0}^{\pi}\sin t dt=2,\ \int_{\frac{\pi}{2}}^{\pi}\sin t dt=1,\ \int_{0}^{2\pi}\sin t dt=0 \\ &\int_{0}^{\frac{\pi}{2}}\sin^2 t dt=\frac{\pi}{4},\ \int_{0}^{\pi}\sin^2 t dt=2\int_{0}^{\frac{\pi}{2}}\sin^2 t dt=\frac{\pi}{2} \\ &\int_{0}^{\frac{3\pi}{2}}\sin^2 t dt=3\int_{0}^{\frac{\pi}{2}}\sin^2 t dt=\frac{3\pi}{4},\ \int_{0}^{2\pi}\sin^2 t dt=4\int_{0}^{\frac{\pi}{2}}\sin^2 t dt=\pi \\ &\int_{0}^{\frac{\pi}{2}}\sin^3 t dt=\frac{2}{3},\ \int_{0}^{\pi}\sin^3 t dt=2\int_{0}^{\frac{\pi}{2}}\sin^3 t dt=\frac{4}{3} \\ &\int_{0}^{\frac{3\pi}{2}}\sin^3 t dt=\frac{2}{3},\ \int_{0}^{2\pi}\sin^3 t dt=0 \\ \\ &②\ \int_{0}^{\frac{\pi}{2}}\cos t dt=1,\ \int_{0}^{\pi}\cos t dt=0,\ \int_{\frac{\pi}{2}}^{\pi}\cos t dt=-1 \\ &\int_{0}^{2\pi}\cos t dt=0 \end{aligned} 三角函数定积分.① ∫02πsintdt=1, ∫0πsintdt=2, ∫2ππsintdt=1, ∫02πsintdt=0∫02πsin2tdt=4π, ∫0πsin2tdt=2∫02πsin2tdt=2π∫023πsin2tdt=3∫02πsin2tdt=43π, ∫02πsin2tdt=4∫02πsin2tdt=π∫02πsin3tdt=32, ∫0πsin3tdt=2∫02πsin3tdt=34∫023πsin3tdt=32, ∫02πsin3tdt=0② ∫02πcostdt=1, ∫0πcostdt=0, ∫2ππcostdt=−1∫02πcostdt=0
③ ∫0πxf(sinx)dx=u=π−x∫π0(π−u)f(sin(π−u))d(π−u)=∫0π(π−u)f(sinu)du2∫0πxf(sinx)dx=∫0ππf(sinu)du∫0πxf(sinx)dx=π2∫0πf(sinu)du=π∫0π2f(sinu)du \begin{aligned} &③\ \int_{0}^{\pi} x f(\sin x) dx \xlongequal{u=\pi - x} \int_{\pi}^{0} (\pi - u) f(\sin(\pi - u)) d(\pi - u) \\ &= \int_{0}^{\pi} (\pi - u) f(\sin u) du \\ \\ &2\int_{0}^{\pi} x f(\sin x) dx = \int_{0}^{\pi} \pi f(\sin u) du \\ &\int_{0}^{\pi} x f(\sin x) dx = \frac{\pi}{2}\int_{0}^{\pi} f(\sin u) du = \pi\int_{0}^{\frac{\pi}{2}} f(\sin u) du \end{aligned} ③ ∫0πxf(sinx)dxu=π−x ∫π0(π−u)f(sin(π−u))d(π−u)=∫0π(π−u)f(sinu)du2∫0πxf(sinx)dx=∫0ππf(sinu)du∫0πxf(sinx)dx=2π∫0πf(sinu)du=π∫02πf(sinu)du
∫02πxf(cosx)dx=u=2π−x∫2π0(2π−u)f(cos(2π−u))d(2π−u)=∫02π(2π−u)f(cosu)du∫02πxf(cosx)dx=12∫02π2πf(cosu)du=π∫02πf(cosu)du∫0πxsin4xdx=π2∫0πsin4xdx=π2⋅2∫0π2sin4xdx=π⋅3!!4!!⋅π2=316π2∫02πxcos4xdx=π∫02πcos4xdx=π⋅4∫0π2cos4xdx=4π⋅3!!4!!⋅π2=4π⋅38⋅π2=34π2 \begin{aligned} &\int_{0}^{2\pi} x f(\cos x) dx \xlongequal{u=2\pi - x} \int_{2\pi}^{0} (2\pi - u) f(\cos(2\pi - u)) d(2\pi - u) \\ &= \int_{0}^{2\pi} (2\pi - u) f(\cos u) du \\ \\ &\int_{0}^{2\pi} x f(\cos x) dx = \frac{1}{2}\int_{0}^{2\pi} 2\pi f(\cos u) du = \pi\int_{0}^{2\pi} f(\cos u) du \\ \\ &\int_{0}^{\pi} x \sin^4 x dx = \frac{\pi}{2}\int_{0}^{\pi} \sin^4 x dx = \frac{\pi}{2} \cdot 2\int_{0}^{\frac{\pi}{2}} \sin^4 x dx \\ &= \pi \cdot \frac{3!!}{4!!} \cdot \frac{\pi}{2} = \frac{3}{16}\pi^2 \\ \\ &\int_{0}^{2\pi} x \cos^4 x dx = \pi\int_{0}^{2\pi} \cos^4 x dx = \pi \cdot 4\int_{0}^{\frac{\pi}{2}} \cos^4 x dx \\ &= 4\pi \cdot \frac{3!!}{4!!} \cdot \frac{\pi}{2} = 4\pi \cdot \frac{3}{8} \cdot \frac{\pi}{2} = \frac{3}{4}\pi^2 \end{aligned} ∫02πxf(cosx)dxu=2π−x ∫2π0(2π−u)f(cos(2π−u))d(2π−u)=∫02π(2π−u)f(cosu)du∫02πxf(cosx)dx=21∫02π2πf(cosu)du=π∫02πf(cosu)du∫0πxsin4xdx=2π∫0πsin4xdx=2π⋅2∫02πsin4xdx=π⋅4!!3!!⋅2π=163π2∫02πxcos4xdx=π∫02πcos4xdx=π⋅4∫02πcos4xdx=4π⋅4!!3!!⋅2π=4π⋅83⋅2π=43π2
【小结】关于三角函数的常用公式:(1) 华里士公式:∫0π2sinnxdx=∫0π2cosnxdx={n−1nn−3n−2⋯12π2, n=2kn−1nn−3n−2⋯23, n=2k+1;(2) ∫0πsinnxdx=2∫0π2sinnxdx,∫0πcosnxdx={2∫0π2cosnxdx, n=2k0, n=2k+1∫02πsinnxdx=∫02πcosnxdx={4∫0π2sinnxdx, n=2k0, n=2k+1(3) ∫0πxf(sinx)dx=π2∫0πf(sinx)dx=π∫0π2f(sinx)dx∫02πxf(cosx)dx=π∫02πf(cosx)dx。 \begin{aligned} &\boxed{【小结】}\text{关于三角函数的常用公式:} \\ &(1)\ \text{华里士公式:}\int_{0}^{\frac{\pi}{2}} \sin^{n}x dx = \int_{0}^{\frac{\pi}{2}} \cos^{n}x dx = \begin{cases} \displaystyle \frac{n-1}{n}\frac{n-3}{n-2}\cdots\frac{1}{2}\frac{\pi}{2},\ &n=2k \\ \displaystyle \frac{n-1}{n}\frac{n-3}{n-2}\cdots\frac{2}{3},\ &n=2k+1 \end{cases}; \\ & \\ &(2)\ \int_{0}^{\pi} \sin^{n}x dx = 2\int_{0}^{\frac{\pi}{2}} \sin^{n}x dx,\int_{0}^{\pi} \cos^{n}x dx = \begin{cases} \displaystyle 2\int_{0}^{\frac{\pi}{2}} \cos^{n}x dx,\ &n=2k \\ 0,\ &n=2k+1 \end{cases} \\ &\quad \int_{0}^{2\pi} \sin^{n}x dx = \int_{0}^{2\pi} \cos^{n}x dx = \begin{cases} \displaystyle 4\int_{0}^{\frac{\pi}{2}} \sin^{n}x dx,\ &n=2k \\ 0,\ &n=2k+1 \end{cases} \\ & \\ &(3)\ \int_{0}^{\pi} x f(\sin x)dx = \frac{\pi}{2}\int_{0}^{\pi} f(\sin x)dx = \pi\int_{0}^{\frac{\pi}{2}} f(\sin x)dx \\ &\quad \int_{0}^{2\pi} x f(\cos x)dx = \pi\int_{0}^{2\pi} f(\cos x)dx。 \end{aligned} 【小结】关于三角函数的常用公式:(1) 华里士公式:∫02πsinnxdx=∫02πcosnxdx=⎩ ⎨ ⎧nn−1n−2n−3⋯212π, nn−1n−2n−3⋯32, n=2kn=2k+1;(2) ∫0πsinnxdx=2∫02πsinnxdx,∫0πcosnxdx=⎩ ⎨ ⎧2∫02πcosnxdx, 0, n=2kn=2k+1∫02πsinnxdx=∫02πcosnxdx=⎩ ⎨ ⎧4∫02πsinnxdx, 0, n=2kn=2k+1(3) ∫0πxf(sinx)dx=2π∫0πf(sinx)dx=π∫02πf(sinx)dx∫02πxf(cosx)dx=π∫02πf(cosx)dx。
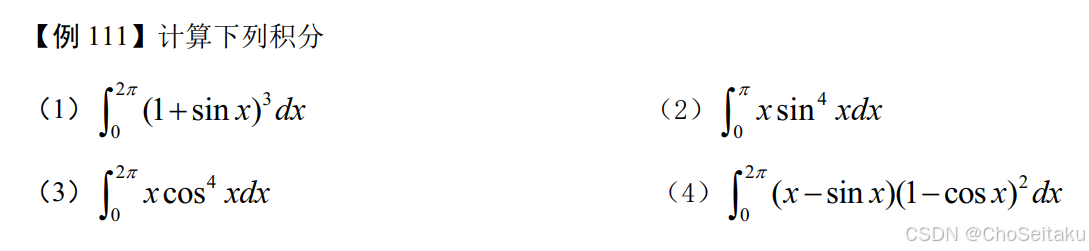
(1) ∫02π(1+sinx)3dx=∫02π(1+3sinx+3sin2x+sin3x)dx=∫02π(1+3sin2x)dx=2π+3⋅4∫0π2sin2xdx=2π+3⋅4⋅π4=5π \begin{aligned} &(1)\ \int_{0}^{2\pi} (1+\sin x)^3 dx \\ &= \int_{0}^{2\pi} \left(1 + 3\sin x + 3\sin^2 x + \sin^3 x\right) dx \\ &= \int_{0}^{2\pi} \left(1 + 3\sin^2 x\right) dx \\ &= 2\pi + 3 \cdot 4\int_{0}^{\frac{\pi}{2}}\sin^2 x dx \\ &= 2\pi + 3 \cdot 4 \cdot \frac{\pi}{4} = 5\pi \end{aligned} (1) ∫02π(1+sinx)3dx=∫02π(1+3sinx+3sin2x+sin3x)dx=∫02π(1+3sin2x)dx=2π+3⋅4∫02πsin2xdx=2π+3⋅4⋅4π=5π
(2)∫0πxsin4xdx=π2∫0πsin4xdx=π2⋅2∫0π2sin4xdx=π⋅3!!4!!⋅π2=316π2(3)∫02πxcos4xdx=π∫02πcos4xdx=π⋅4∫0π2cos4xdx=4π⋅3!!4!!⋅π2=4π⋅38⋅π2=34π2 \begin{aligned} &(2)\int_{0}^{\pi} x \sin^4 x dx = \frac{\pi}{2}\int_{0}^{\pi} \sin^4 x dx = \frac{\pi}{2} \cdot 2\int_{0}^{\frac{\pi}{2}} \sin^4 x dx \\ &= \pi \cdot \frac{3!!}{4!!} \cdot \frac{\pi}{2} = \frac{3}{16}\pi^2 \\ \\ &(3)\int_{0}^{2\pi} x \cos^4 x dx = \pi\int_{0}^{2\pi} \cos^4 x dx = \pi \cdot 4\int_{0}^{\frac{\pi}{2}} \cos^4 x dx \\ &= 4\pi \cdot \frac{3!!}{4!!} \cdot \frac{\pi}{2} = 4\pi \cdot \frac{3}{8} \cdot \frac{\pi}{2} = \frac{3}{4}\pi^2 \end{aligned} (2)∫0πxsin4xdx=2π∫0πsin4xdx=2π⋅2∫02πsin4xdx=π⋅4!!3!!⋅2π=163π2(3)∫02πxcos4xdx=π∫02πcos4xdx=π⋅4∫02πcos4xdx=4π⋅4!!3!!⋅2π=4π⋅83⋅2π=43π2
(4) =∫02πx(1−cosx)2dx−∫02πsinx(1−cosx)2dx=π∫02π(1−cosx)2dx−13(1−cosx)3∣02π=π∫02π(1−2cosx+cos2x)dx=π∫02π(1+cos2x)dx=π(2π+4∫0π2cos2xdx)=π(2π+4⋅π4)=3π2 \begin{aligned} &(4)\ = \int_{0}^{2\pi} x(1-\cos x)^2 dx - \int_{0}^{2\pi} \sin x(1-\cos x)^2 dx \\ &= \pi\int_{0}^{2\pi}(1-\cos x)^2 dx - \frac{1}{3}(1-\cos x)^3\bigg|{0}^{2\pi} \\ &= \pi\int{0}^{2\pi}\left(1 - 2\cos x + \cos^2 x\right) dx \\ &= \pi\int_{0}^{2\pi}\left(1 + \cos^2 x\right) dx \\ &= \pi\left(2\pi + 4\int_{0}^{\frac{\pi}{2}}\cos^2 x dx\right) \\ &= \pi\left(2\pi + 4 \cdot \frac{\pi}{4}\right) = 3\pi^2 \end{aligned} (4) =∫02πx(1−cosx)2dx−∫02πsinx(1−cosx)2dx=π∫02π(1−cosx)2dx−31(1−cosx)3 02π=π∫02π(1−2cosx+cos2x)dx=π∫02π(1+cos2x)dx=π(2π+4∫02πcos2xdx)=π(2π+4⋅4π)=3π2

证:(1) ∫−aaf(x)g(x)dx=u=−x∫a−af(−u)g(−u)d(−u)=∫−aaf(−u)g(u)du=12∫−aa(f(x)+f(−x))g(x)dx=A2∫−aag(x)dx=A∫0ag(x)dx \begin{aligned} &\text{证:}(1)\ \int_{-a}^{a} f(x)g(x) dx \xlongequal{u=-x} \int_{a}^{-a} f(-u)g(-u) d(-u) \\ &= \int_{-a}^{a} f(-u)g(u) du = \frac{1}{2}\int_{-a}^{a} \left(f(x)+f(-x)\right)g(x) dx \\ &= \frac{A}{2}\int_{-a}^{a} g(x) dx = A\int_{0}^{a} g(x) dx \end{aligned} 证:(1) ∫−aaf(x)g(x)dxu=−x ∫a−af(−u)g(−u)d(−u)=∫−aaf(−u)g(u)du=21∫−aa(f(x)+f(−x))g(x)dx=2A∫−aag(x)dx=A∫0ag(x)dx
arctanx+arctan1x=π2tanα=x, α=arctanxtanβ=1x, β=arctan1xarctanex+arctane−x=π2 \begin{aligned} &\arctan x + \arctan \frac{1}{x} = \frac{\pi}{2} \\ \\ &\tan\alpha = x,\ \alpha = \arctan x \\ &\tan\beta = \frac{1}{x},\ \beta = \arctan \frac{1}{x} \\ \\ &\arctan e^x + \arctan e^{-x} = \frac{\pi}{2} \end{aligned} arctanx+arctanx1=2πtanα=x, α=arctanxtanβ=x1, β=arctanx1arctanex+arctane−x=2π
(2) ∫−π2π2∣sinx∣arctanexdx=π2∫0π2sinxdx=π2 \begin{aligned} &(2)\ \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} |\sin x| \arctan e^x dx = \frac{\pi}{2}\int_{0}^{\frac{\pi}{2}} \sin x dx = \frac{\pi}{2} \end{aligned} (2) ∫−2π2π∣sinx∣arctanexdx=2π∫02πsinxdx=2π
【小结】对于对称区间上的积分,如果被积函数本身不具有奇偶性,同时也不便于直接计算,则可以使用公式∫−aaf(x)dx=∫0a[f(x)+f(−x)]dx进行计算。对于该公式,如果是解答题,则使用的时候需要首先进行证明。 \begin{aligned} &\boxed{【小结】}\text{对于对称区间上的积分,如果被积函数本身不具有奇偶性,同时也不便于直接} \\ &\text{计算,则可以使用公式}\int_{-a}^{a} f(x)dx = \int_{0}^{a} \left[ f(x) + f(-x) \right]dx\text{进行计算。对于该公式,如果} \\ &\text{是解答题,则使用的时候需要首先进行证明。} \end{aligned} 【小结】对于对称区间上的积分,如果被积函数本身不具有奇偶性,同时也不便于直接计算,则可以使用公式∫−aaf(x)dx=∫0a[f(x)+f(−x)]dx进行计算。对于该公式,如果是解答题,则使用的时候需要首先进行证明。