今日课程提纲:
今天是强化学习纲要课程的第三课。我将给大家介绍model free prediction and control。就是在没有模型 的条件下,怎么进行预测跟控制。上一次课我给大家介绍了MDP,然后给定一个policy怎么去衡量一个policy的价值。然后也介绍了两种常见的MDP控制的算法,就policy iteration以及value iteration。
这里有一个很重要的不同是,我们是不是已知MDP ,因为知不知道这个MDP会对我们选择算法有非常重要的影响。因为在现实生活中,大部分的MDP其实都没有现成的模型可以用,所以我们只能用model free 的办法。

目录
- 一、回顾已知MDP的解法
- [二、Model free](#二、Model free)
-
- [2.1 Model-free prediction](#2.1 Model-free prediction)
-
- [2.1.1 蒙特卡罗Monte-Carlo policy evaluation](#2.1.1 蒙特卡罗Monte-Carlo policy evaluation)
一、回顾已知MDP的解法
首先来看一下上一次讲的MDP控制算法。我们什么时候说一个MDP已知呢?就是说在MDP马尔科夫决策过程中,它的奖励函数R跟它的转移矩阵P都是暴露给这个agent。所以agent可以通过policy iteration以及value iteration来寻找最佳的策略。这里是policy iteration的算法的一个总结。Policy iteration算法包含了两部分,一部分是policy evaluation,就是给定当前算法,我们利用这个bellman expectation backup来更新我们的价值函数。这样我们就可以通过迭代的办法得到在当前这个策略下面,每一个状态的价值是什么。
当我们得到了这个价值函数过后,然后算它的Q函数,进行第二步的策略的改进。就policy improvement,就通过采取贪心策略,在这个Q函数上面进行贪心策略arg max这个操作来进行改变它的策略。在这两个过程中,这个奖励函数以及转移矩阵都是暴露给agent(红色高亮),在这两个算法过程中,都是这个奖励函数跟转移函数都是暴露给agent。

Value iteration的具体步骤。在value iteration是利用Bellman Optimality backup来更新这个价值函数。在这个过程中迭代过程中,并没有任何策略的引入。是当把这个max操作运行很多很多次过后,得到对于每一个状态的价值函数。当得到价值函数过后,再利用一个policy retrieve的一个过程,这样得到它的最佳策略。
在这两个步骤之中,大家也可以看到价值函数以及状态转移矩阵都是暴露给Agent。因为在这个等式里面都包含了这价值函数跟转移矩阵。所以在进行policy iteration以及value iteration的过程中,价值函数以及转移矩阵是必不可少的。所以这两种算法都是只能在我们已知MDP模型的情况下进行计算。

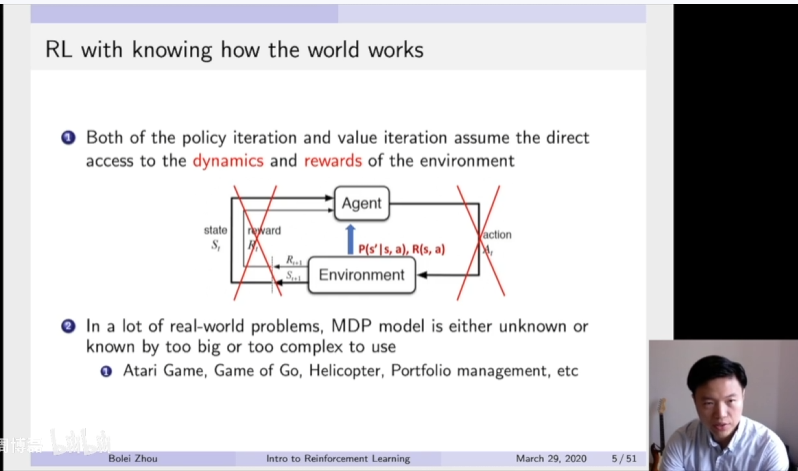
所以看到policy iteration以及value iteration都需要直接得到转移环境的这个dynamics以及它的奖励函数 。所以在这个过程中,其实我们并没有让agent直接跟环境environment进行交互,就并没有用到强化学习的这个diagram。通过这个交互过程然后得到信息。这里更像是在agent找到一个捷径。他直接去通过这个后门获取它的这个转移矩阵以及这个奖励函数来进行迭代的计算到每个状态以及最佳的策略。
但是在很多现实实际的问题中,MDP的模型并不已知,或者模型太大,以至于不能进行迭代的计算。就比如说很多现实生活中,比如说这个atari game,以及这个围棋,还有控制直升飞机,一些股票交易的这些问题,都是状态整个转移太复杂了,并没有一个简明的一个函数。所以在这种情况下面,只能利用model free强化学习的方法去解。
二、Model free
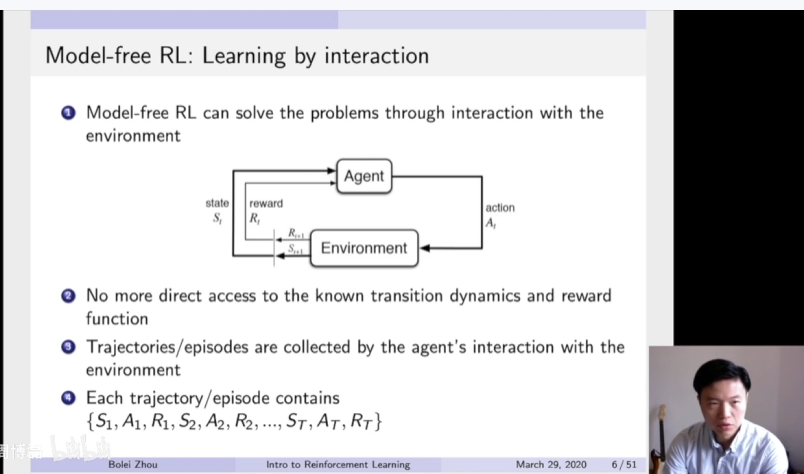
Model free强化学习方法就是利用了这个经典的diagram,就agent通过跟环境进行交互获得这个观测以及获得奖励来调整他的行为。通过一系列的观测收集到的数据来调整它的策略。所以在model free强化学习方法里面,并没有直接获取整个环境的转移状态以及它的奖励函数。是通过让Agent跟环境进行一定的交互,然后采集到了很多的轨迹数据。这里的轨迹数据可以表征成他的起始状态,然后在状态的采取的行为以及他获得的奖励。这样每一步他的一个反馈,得到了这样一个轨迹。那么这个agent就需要从这样的轨迹里面去获取信息,然后改进它的策略,以至于他可以获得更多的奖励。这就是model free prediction and control的一个问题。怎么从通过跟环境的交互获得这些轨迹数据中,然后去估计一个状态的价值,以及进一步改进策略。
2.1 Model-free prediction
首先来看一下Model-free prediction,就是当给定一个策略的时候,怎么去估计它的价值。而且是在没法获取MDP转移模型的情况下。这里有两种常见的方法,一种是蒙特卡罗policy evaluation的方法,另外一种是Temporal Difference TD learning的方法。

2.1.1 蒙特卡罗Monte-Carlo policy evaluation
首先是基于蒙特卡罗采样的一个policy evaluation。之前两次课程我也给大家简短的提过,蒙特卡罗方法主要是基于采样的方法,就是让这个agent跟环境进行交互,就会得到很多轨迹,然后每一个轨迹都会得到一个实际的收益。我们实际知道采取的这些行为它到底有没有收益,然后直接从获取的这个实际收益来估计每一个状态的价值。所以这个蒙特卡罗Monte-Carlo policy evaluation也是类似的方法。
在算取它在每一个轨迹得到的实际的return过后,直接可以把很多轨迹的return进行一个平均。那么就可以知道在某一个策略下面,它对应的这个状态的价值。所以这里MC policy evaluation就是利用这个empirical mean return的方法来估计它。就通过这个agent和环境交互,得到了很多轨迹,得到了实际的return,然后来估算它每一个状态的价值。所以MC这种方法的话,它并不需要这个马尔科夫决策过程的转移函数以及它的奖励函数。而且也不需要像这个动态回归dynamics programming,用这种bootstripping的方法来普及他。

这里MC一个局限性就是说它只能用在一些马尔科夫决策过程,就是可以有终止的马尔可夫决策过程。

这里是马尔科夫policy evaluation的一个简单的算法概括。就是当要估计某一个状态的时候,那么就从这个状态开始,然后通过数数的办法就数数这个状态被访问了多少次,然后从这个状态开始总共得到了多少的return,最后再取一个empirical mean,然后就会得到每个状态的价值。通过大数定律,最终得到足够的轨迹过后,就可以趋近这个策略对应的这个价值函数。


这里可以把empirical mean写成一种这种逐步叠加mean incremental mean的一个办法。比如说现在要估计一个数的平均,那就通过可以采样很多很多次。比如说这个μt可以直接平均,可以把这个平均进行一个分解,就是把这个加和分解成它最新的获得的这个XT的值。加它之前从最开始到T-1的这个值,然后我们再可以把上一个时刻它的平均值也带入进去。后面的这个加和值从一加到T-1,这个加和值就等于T-1乘以它上一个时刻的平均值,这样就可以把上一时刻的平均值跟现在的这个时刻的平均值建立一个联系。
这样你就可以发现,就可以通过类似于这种mean average的一个办法。当你得到新的一个XT这个值的时候,然后我们跟上一个平均值进行相减。然后用这个差值作为一个残差,然后乘以一个learning rate,然后加到我们当前的这个平均值,然后就会更新现在值。这是一个小的一个转换,但是通过这种转换,就可以把上一时刻的值跟跟上一时跟这一时刻得到更新的这个值建立一个更新的一个联系。

可以把蒙特卡罗更新的这个方法也写成这种incremental MC的一个方法。当我们一直在在跑这个采集数据,然后得到了一个新的轨迹过后,得到了这个新的轨迹。可以在这个轨迹上面的每一个state上面,让它访问的数这个counter加个一,以及它当前对于这个值,也可以用incremental这种增量的办法去更新它的值。这样你可以发现,我们甚至可以把一除以它的这个counting变成一个阿尔法值。这个阿尔法值是learning rate,学习效率,希望它的值跟更新的速率有多快,然后这个值就可以相应的进行设置。所以这里是这个算法,就是增量MC update的一个算法。

MC与DP的差别
然后我们再来看一下MC跟DP办法的一个差异。dynamic program动态规划这个方法也是一个很常用的来估计某一个价值函数的方法,就给定了某一个策略,来估计它的价值函数。在动态规划里面,是利用了这个Bootstrapping。Bootstrapping翻译成中文是拔靴自助。意思就是要估计一个量,估计这个量是基于之前估计的这个量,就更像we estimate on top of previous estimate,这个是Bootstrapping的一个概念。就要估计一个量,然后通过之前估计的量然后进行得迭代,就希望它最后可以收敛。
所以这个Dynamic programming用的就是bellman expectation backup,就通过它上一时刻Vi-1状态的值,然后更新到它当前时刻Vi这个值。就通过不停的迭代,就希望他最后可以收敛。然后你可以发现这个expectation backup就是把前面一步所有的状态都加和起来了。这里有一个内部加和,先把每个状态转移,然后加了上去。然后还有一个外部加和,外部加和是把基于它每个策略都加和上去,这样就算了两次的这种expectation,然后得到了它的一个更新。
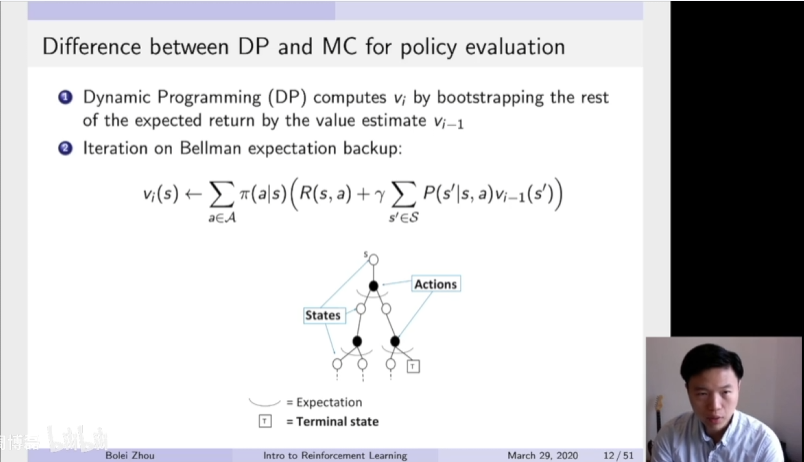
但MC是通过它的一个empirical mean return,就它实际得到的收益来更新它。然后在这个数上面就是更像是得到了一个比如说这个蓝色轨迹。因为得到的是实际的一条轨迹,实际的轨迹它上面它的状态就已经是决定了,就是他每一个时刻他采取了什么行为,以及他到达了什么状态都是决定的。所以MC得到的是一条轨迹,这个轨迹在这个数上面表示出来就是一个蓝色的从起始然后到最后终止状态的一个轨迹。现在只是更新在这个轨迹上面的所有状态,就利用它得到的实际价值来更新这个轨迹上面的所有状态。而跟这个轨迹没有关系的这些状态都没有进行更新。

MC优势
我们再来看一下MC相对于DP方法有什么样的好处。MC首先可以在不知道的环境下,就MDP的转移矩阵以及奖励函数不知道的情况下面进行估计。所以MC可以是model free的一个方法。但是DP是必须需要知道它的这个转移矩阵,所以它是比较难在model free状态情况下面工作。
另外一点是MC这个方法,因为每次只需要在更新这一个轨迹上面,它的所有状态。而所有已知的状态,跟它没有相关的状态,我们是不用关心的。所以这就极大的减少了更新的成本。因为一条轨迹上面可能就只有十几个或者几十个状态,我们就把它更新就好。但是对于DP这个算法的话,它是算了两次加和。这样就需要把整个MDP里面所有状态都加和一遍迭代一遍,然后这样才能更新。这样在很多时候MDP状态下面,如果状态数量非常多,比如说有100万个或者200万个,这样去迭代swapping一天的话,速度是非常慢的。所以这也是我们通过这个sample base的方法去更新的一个优势,就MC相对于DP的一个优势。

