Daily算法刷题【面试经典150题-5️⃣图】

释怀°Believe2025-12-09 20:16

文章目录

  • 📕图
    • [1.1 岛屿数量(dfs/bfs/并查集)](#1.1 岛屿数量(dfs/bfs/并查集))
  • [1.2 被围绕的区域](#1.2 被围绕的区域)
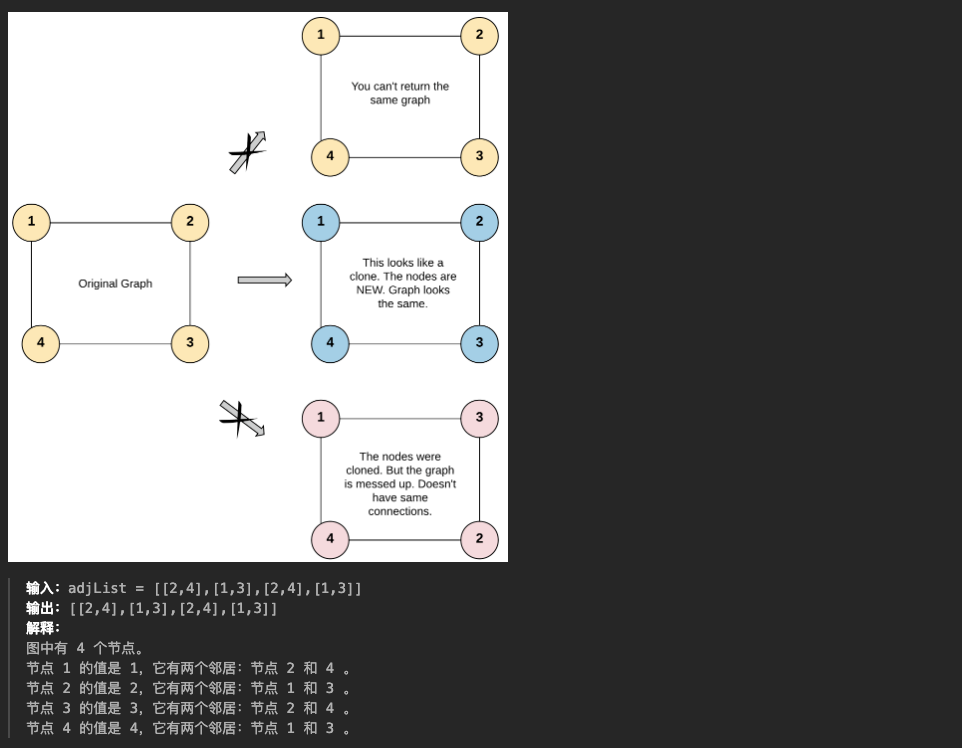
    • [1.3 克隆图](#1.3 克隆图)

📕图

1.1 岛屿数量(dfs/bfs/并查集)

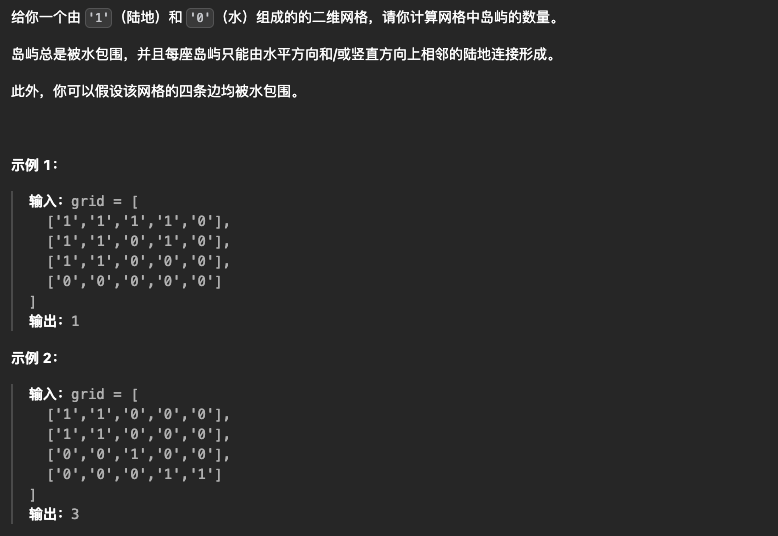
法1:dfs

cpp 复制代码 
class Solution {
public:
    vector<vector<bool>> vis;
    int dx[4] = {-1,1,0,0};
    int dy[4] = {0,0,-1,1};
    void dfs(vector<vector<char>>& grid,int x,int y){
        vis[x][y] = true;
        int m = grid.size();
        int n = grid[0].size();
        for(int k = 0; k < 4; k++){
            int nx = x + dx[k];
            int ny = y + dy[k];
            if(nx>=0&&nx<m&&ny>=0&&ny<n&&grid[nx][ny]=='1'&&vis[nx][ny]==false){
                dfs(grid,nx,ny);
            }
        }
    }
    int numIslands(vector<vector<char>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        int ans = 0;
        vis.assign(m,vector<bool>(n,false));
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == '1' && vis[i][j] == false){
                    dfs(grid,i,j);
                    ans++;
                }
            }
        }
        return ans;
    }
};

法2:bfs

cpp 复制代码 
class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int m = grid.size();
        if(m==0) return 0;
        int n = grid[0].size();
        int ans = 0;

        int dx[4] = {-1,1,0,0};
        int dy[4] = {0,0,-1,1};
        vector<vector<bool>> vis(m, vector<bool>(n, false));

        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == '1'  && vis[i][j] == false){
                    ans++;
                    queue<pair<int,int>> q;
                    q.push({i,j});
                    vis[i][j] = true;

                    while(!q.empty()){
                        // 方法1
                        // auto [x,y] = q.front();
                        // 方法2：
                        // pair<int,int> cur = q.front();
                        // int x = cur.first;
                        // int y = cur.second;
                        int x = q.front().first;
                        int y = q.front().second;
                        

                        q.pop();
                        for(int k = 0; k < 4; k++){
                            int nx = x + dx[k];
                            int ny = y + dy[k];
                            if(nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
                            if(vis[nx][ny]==false && grid[nx][ny] == '1'){
                                vis[nx][ny] = true;
                                q.push({nx,ny});
                            }
                        }
                    }
                }
            }
        }
        return ans;
    }
};

法3:并查集

cpp 复制代码 
class Solution {
public:
    vector<int> parent;
    vector<int> rank;  //类似于树高，为了更快的效率。让树尽可能矮一些

    // 并查集 find（带路径压缩）
    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    // 并查集 union（按秩合并），顺便维护 count
    void unite(int x, int y, int &count) {
        int fa_x = find(x);
        int fa_y = find(y);
        if (fa_x == fa_y) return;   // 已经在一个集合里了

        if (rank[fa_x] < rank[fa_y]) {
            parent[fa_x] = fa_y;
        } else if (rank[fa_x] > rank[fa_y]) {
            parent[fa_y] = fa_x;
        } else {
            parent[fa_y] = fa_x;
            rank[fa_x]++;
        }
        count--;                // 两个集合合并成一个，集合数 -1
    }

    int numIslands(vector<vector<char>>& grid) {
        int m = grid.size();
        if (m == 0) return 0;
        int n = grid[0].size();

        parent.resize(m * n);
        rank.assign(m * n, 0);

        // 初始化 parent
        for (int i = 0; i < m * n; i++) {
            parent[i] = i;
        }

        int count = 0;  // 记录当前有多少个"岛集合"

        // 先数一共有多少个 '1'，每个先当作一个独立岛
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == '1') {
                    count++;
                }
            }
        }

        int dx[4] = {-1, 1, 0, 0};
        int dy[4] = {0, 0, -1, 1};

        // 再把相邻的 '1' 合并
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == '1') {
                    int id1 = i * n + j;   // (i, j) 映射成一维编号

                    for (int k = 0; k < 4; k++) {
                        int nx = i + dx[k];
                        int ny = j + dy[k];
                        if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
                        if (grid[nx][ny] == '1') {
                            int id2 = nx * n + ny;
                            unite(id1, id2, count);
                        }
                    }
                }
            }
        }

        return count;
    }
};

类实现并查集

cpp 复制代码 
class UnionFind {
public:
    vector<int> parent;
    vector<int> rank;
    int count;   // 当前集合数量 = 岛屿数量

    UnionFind(int n) {
        parent.resize(n);
        rank.assign(n, 0);
        count = 0;
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    void unite(int x, int y) {
        int rx = find(x);
        int ry = find(y);
        if (rx == ry) return;

        if (rank[rx] < rank[ry]) {
            parent[rx] = ry;
        } else if (rank[rx] > rank[ry]) {
            parent[ry] = rx;
        } else {
            parent[ry] = rx;
            rank[rx]++;
        }
        count--;   // 两个集合合并成一个
    }
};

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int m = grid.size();
        if (m == 0) return 0;
        int n = grid[0].size();

        UnionFind uf(m * n);

        int dx[4] = {-1, 1, 0, 0};
        int dy[4] = {0, 0, -1, 1};

        // 先统计所有 '1'，每个当成一个独立的集合
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == '1') {
                    uf.count++;
                }
            }
        }

        // 合并相邻的 '1'
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == '1') {
                    int id1 = i * n + j;
                    for (int k = 0; k < 4; k++) {
                        int ni = i + dx[k];
                        int nj = j + dy[k];
                        if (ni < 0 || ni >= m || nj < 0 || nj >= n) continue;
                        if (grid[ni][nj] == '1') {
                            int id2 = ni * n + nj;
                            uf.unite(id1, id2);
                        }
                    }
                }
            }
        }

        return uf.count;
    }
};

1.2 被围绕的区域

法1:dfs

cpp 复制代码 
/*
    dfs:
    所有不会被围住的 'O'，一定是跟边界上的 'O' 通过上下左右连在一起的。
    剩下那些没连到边界的 'O'，就是被围住的，全部改成 'X'。
    1.从四条边出发，标记"安全的 O":只要在边上看到 'O'，就从这里做 DFS / BFS，
    把所有与它连通的 'O' 都标记成特殊字符（比如 '#'），表示这些是不能被翻的 O。
    2.再全图遍历一遍，如果是'O'.说明它既不是边界 O，也没被边界 O 的 DFS 标记到,则改为'X'

*/
class Solution {
public:
    int n,m;
    int dx[4] = {-1,1,0,0};
    int dy[4] = {0,0,-1,1};

    void dfs(vector<vector<char>>& board,int x,int y){
        board[x][y] = '#';
        for(int k = 0; k < 4; k++){
            int nx = x + dx[k];
            int ny = y + dy[k];
            if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
            if(board[nx][ny] == 'O') dfs(board,nx,ny);
        }
    }
    void solve(vector<vector<char>>& board) {
        n = board.size();
        if(n == 0) return;
        m = board[0].size();

        // 第1行和最后1行
        for(int i = 0; i < m; i++){
            if(board[0][i] == 'O') dfs(board,0,i);
            if(board[n-1][i] == 'O') dfs(board,n-1,i);
        }

        //第1列和最后列行
        for(int j = 0; j < n ; j++){
            if(board[j][0] == 'O') dfs(board,j,0);
            if(board[j][m-1] == 'O') dfs(board,j,m-1);
        }

        for(int i = 0; i < n ;i++){
            for(int j = 0; j < m; j++){
                if(board[i][j] == 'O') board[i][j] = 'X';
                else if(board[i][j] == '#') board[i][j] = 'O';
            }
        }
    }
};

法2:bfs

cpp 复制代码 
/*
    BFS 版思路和 DFS 完全一样：
    1. 从四条边上所有的 'O' 出发，用 BFS 把和它们连通的 'O' 都标成 '#'
       ------这些是"安全的 O"，不会被围住。
    2. 再遍历一遍棋盘：
       - 还剩下的 'O' 都是被围住的，改成 'X'
       - '#' 还原成 'O'
*/

class Solution {
public:
    int n, m;
    int dx[4] = {-1, 1, 0, 0};
    int dy[4] = {0, 0, -1, 1};

    void bfs(vector<vector<char>>& board, int sx, int sy) {
        queue<pair<int,int>> q;
        q.push({sx, sy});
        board[sx][sy] = '#';   

        while (!q.empty()) {
            pair<int,int> cur = q.front();
            q.pop();
            int x = cur.first;
            int y = cur.second;

            for (int k = 0; k < 4; k++) {
                int nx = x + dx[k];
                int ny = y + dy[k];

                if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
                if (board[nx][ny] == 'O') {
                    board[nx][ny] = '#';
                    q.push({nx, ny});
                }
            }
        }
    }

    void solve(vector<vector<char>>& board) {
        n = board.size();
        if (n == 0) return;
        m = board[0].size();

        // 1. 从四条边上的 'O' 出发，BFS 标记所有"安全的 O"为 '#'

        // 第一行 和 最后一行
        for (int j = 0; j < m; j++) {
            if (board[0][j] == 'O') bfs(board, 0, j);
            if (board[n - 1][j] == 'O') bfs(board, n - 1, j);
        }

        // 第一列 和 最后一列
        for (int i = 0; i < n; i++) {
            if (board[i][0] == 'O') bfs(board, i, 0);
            if (board[i][m - 1] == 'O') bfs(board, i, m - 1);
        }

        // 2. 再扫一遍棋盘：

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == 'O') board[i][j] = 'X';
                else if (board[i][j] == '#') board[i][j] = 'O';
            }
        }
    }
};

1.3 克隆图


相关推荐
List<String> error_P2 小时前
数据结构：链表-单向链表篇
算法·链表
ss2732 小时前
ConcurrentHashMap：扩容机制与size()方法
算法·哈希算法
2401_860319522 小时前
在React Native鸿蒙跨平台开发中实现一个冒泡排序算法并将其应用于数据排序，如何进行复制数组以避免直接修改状态中的数组
javascript·算法·react native·react.js·harmonyos
im_AMBER2 小时前
Leetcode 72 数组列表中的最大距离
c++·笔记·学习·算法·leetcode
学历真的很重要2 小时前
PyTorch 机器学习工作流程基础 - 完整教程
人工智能·pytorch·后端·python·深度学习·机器学习·面试
编程饭碗2 小时前
【Java循环】
java·服务器·算法
曾几何时`2 小时前
归并排序（一）
数据结构·算法·leetcode
dragoooon343 小时前
仿muduo库实现高并发服务器-面试常见问题
运维·服务器·面试
Dream it possible！3 小时前
LeetCode 面试经典 150_图的广度优先搜索_最小基因变化（93_433_C++_中等）（广度优先搜索（BFS））
c++·leetcode·面试·广度优先
热门推荐
01GitHub 镜像站点02【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04UV安装并设置国内源05React CVE-2025-55182漏洞排查与修复指南06Linux下V2Ray安装配置指南07BongoCat - 跨平台键盘猫动画工具08从入门到实战：Gemini 3 使用指南速览09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）10本地部署阿里最新开源的Z-Image