强化学习入门-5(MAPPO)

多智能体强化学习项目-5-simple_spread-v3(MAPPO)

环境

本环境是 PettingZoo 库中 MPE (Multi-Agent Particle Environments) 系列的一个经典多智能体协作环境。

官网链接：https://pettingzoo.farama.org/environments/mpe/simple_spread/

任务描述：

这是一个 完全合作（Cooperative) 的任务。

环境中有 N N N 个智能体（Agents，通常为紫色圆圈）和 N N N 个地标（Landmarks，通常为黑色圆点）。
目标是让智能体通过移动，覆盖所有的地标（每个地标上至少有一个智能体）。
同时，智能体之间需要避免发生碰撞。

操作 (Action Space)：

设置为离散动作空间 (continuous_actions=False) 时，每个智能体的动作空间大小为 5：

0: 什么都不做 (No-op)
1: 向左移动 (Move Left)
2: 向右移动 (Move Right)
3: 向下移动 (Move Down)
4: 向上移动 (Move Up)

对应状态向量 (Observation Space)

对于环境中的每一个智能体 i i i，其观测向量 o i o_i oi 包含了自己的物理状态以及与其他物体（地标、队友）的相对位置信息。

假设有 N N N 个智能体和 N N N 个地标，单个智能体的观测向量结构如下：

o i = [ v x , v y p x , p y l 1 x , l 1 y ⋮ l N x , l N y a 1 x , a 1 y ⋮ a k x , a k y ] o_i = \left[ \begin{aligned} v_x, v_y \\[4pt] p_x, p_y \\[4pt] l_{1x}, l_{1y} \\[4pt] \vdots \\[4pt] l_{Nx}, l_{Ny} \\[4pt] a_{1x}, a_{1y} \\[4pt] \vdots \\[4pt] a_{kx}, a_{ky} \end{aligned} \right] oi= vx,vypx,pyl1x,l1y⋮lNx,lNya1x,a1y⋮akx,aky

v x , v y v_x, v_y vx,vy : 智能体自身的在 x, y 轴上的速度 (2维)
p x , p y p_x, p_y px,py : 智能体自身的在 x, y 轴上的绝对位置 (2维)
l j x , l j y l_{jx}, l_{jy} ljx,ljy : 所有地标 相对于该智能体的相对位置向量 ( N × 2 N \times 2 N×2 维)
a k x , a k y a_{kx}, a_{ky} akx,aky : 其他队友 相对于该智能体的相对位置向量 ( ( N − 1 ) × 2 (N-1) \times 2 (N−1)×2 维)
(通讯位): 在某些配置下可能包含其他智能体的通讯信息，但在标准 simple_spread 中通常为空或不启用。

维度计算示例 (3智能体 3地标):
2 ( 速度 ) + 2 ( 位置 ) + 3 × 2 ( 地标相对位置 ) + 2 × 2 ( 队友相对位置 ) = 18 2(速度) + 2(位置) + 3 \times 2(地标相对位置) + 2 \times 2(队友相对位置) = 18 2(速度)+2(位置)+3×2(地标相对位置)+2×2(队友相对位置)=18 维。

奖励函数 (Reward Function)：

该环境采用全局共享奖励（所有智能体获得的奖励值是相同的），以鼓励合作。

覆盖奖励（距离惩罚） ：根据每个地标距离其最近的智能体的距离之和计算。
- R c o v e r = − ∑ j = 1 N min ⁡ i ( dist ( a g e n t i , l a n d m a r k j ) ) R_{cover} = -\sum\limits_{j=1}^{N} \min_{i} (\text{dist}(agent_i, landmark_j)) Rcover=−j=1∑Nmini(dist(agenti,landmarkj))
- 也就是：大家要把所有坑都填上，距离坑越近，惩罚越小（分越高）。
碰撞惩罚 ：如果两个智能体发生重叠（碰撞）。
- 每次碰撞： − 1 -1 −1 (该数值可能随版本微调，通常是固定的惩罚值)。

总奖励 = 覆盖奖励 + 碰撞惩罚

引入环境

下载包

PettingZoo 是 Gymnasium 的多智能体版本。

text 复制代码

pip install pettingzoo[mpe]

导入

注意：多智能体通常使用 parallel_env 来支持并行训练（如 MAPPO）。

python 复制代码

from pettingzoo.mpe import simple_spread_v3

# 创建并行环境
# continuous_actions=False 表示使用离散动作(0-4)
# render_mode="human" 用于显示画面，训练时建议设为 None
env = simple_spread_v3.parallel_env(N=3, local_ratio=0.5, max_cycles=25, continuous_actions=False, render_mode="human")

# 重置环境
observations, infos = env.reset()

# 获取维度信息 (以第一个智能体为例)
agents = env.possible_agents
n_agents = len(agents)
obs_dim = env.observation_space(agents[0]).shape[0] # 例如 18
action_dim = env.action_space(agents[0]).n          # 例如 5

MAPPO算法

与PPO的区别

虽然此时为多智能体环境，但此时仍然采用Actor-Critic算法作为基础，但此时两个网络的功能如下：

Actor: 输入局部信息，输出对应的动作(即对于每个智能体，均使用该网络对动作进行预测)
Critic: 输入全局信息(即所有智能体的状态集合)，输出预测价值

激活函数选择

对于ReLu激活函数而言，一旦出现负数，那么输出为0，同时梯度也为0，那么在强化学习中可能会导致智能体在环境中的某些区域停止学习或无法探索新的动作，导致策略陷入局部最优解甚至是崩溃。

而Tanh 的优势为：虽然 Tanh 在饱和区（极值）梯度也会变小，但它处处可导且几乎不会完全"死掉"（除非数值溢出），这保证了梯度的持续流动。

因此这里选择Tanh激活函数。

改进GAE

前面使用的GAE将两种结束直接通过或运算计算得到的值作为done值的选择，但是对于模型而言，正常到达回合上限的操作往往是较好的行动，而此时若乘上 0 0 0将优势消除反而会告诉模型这个行为一文不值，就可能会导致模型最终无法收敛。

因此，这里额外传入terminations作为结束标志，用于更准确的计算得到优势。

代码如下：

python 复制代码

    def GAE(self, global_obs, next_global_obs, rewards, dones, terminations):
        rewards = torch.as_tensor(rewards, dtype=torch.float32, device=self.device)
        dones = torch.as_tensor(dones, dtype=torch.float32, device=self.device)
        terminations = torch.as_tensor(terminations, dtype=torch.float32, device=self.device)
        with torch.no_grad():
            values = self.critic(global_obs)
            next_values = self.critic(next_global_obs)

        T = rewards.shape[0]
        advantages = torch.zeros_like(rewards, device=self.device)
        gae = torch.zeros(1, device=self.device)
        for t in reversed(range(T)):
            mask_value = 1.0 - terminations[t]
            mask_traj = 1.0 - dones[t]

            delta = rewards[t] + self.gamma * next_values[t] * mask_value - values[t]
            gae = delta + self.gamma * self.lamda * mask_traj * gae

            advantages[t] = gae

        returns = advantages + values
        return advantages, returns

MAPPO类

MAPPO的总体操作与PPO类似，但要注意此时数据的维度调整。

python 复制代码

class MAPPO():
    def __init__(self,obs_dim, action_dim, n_agents, hidden_dim=64, actor_lr = 3e-4, critic_lr = 3e-4, gamma = 0.99, lamda = 0.95, epsilon = 0.2, K_epochs = 4, batch_size = 128):
        self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
        self.n_agents = n_agents
        self.global_obs_dim = obs_dim * n_agents
        self.obs_dim = obs_dim
        self.action_dim = action_dim
        self.hidden_dim = hidden_dim
        self.gamma = gamma
        self.lamda = lamda
        self.epsilon = epsilon
        self.K_epochs = K_epochs
        self.batch_size = batch_size
        self.c1_vf = 0.5
        self.c2_entropy = 0.01
        self.actor = Actor(self.obs_dim, self.action_dim, self.hidden_dim).to(self.device)
        self.critic = Critic(self.global_obs_dim, self.hidden_dim).to(self.device)
        self.actor_optimizer = optim.Adam(self.actor.parameters(), actor_lr)
        self.critic_optimizer = optim.Adam(self.critic.parameters(), critic_lr)

    def GAE(self, global_obs, next_global_obs, rewards, dones, terminations):
        rewards = torch.as_tensor(rewards, dtype=torch.float32, device=self.device)
        dones = torch.as_tensor(dones, dtype=torch.float32, device=self.device)
        terminations = torch.as_tensor(terminations, dtype=torch.float32, device=self.device)
        with torch.no_grad():
            values = self.critic(global_obs)
            next_values = self.critic(next_global_obs)

        T = rewards.shape[0]
        advantages = torch.zeros_like(rewards, device=self.device)
        gae = torch.zeros(1, device=self.device)
        for t in reversed(range(T)):
            mask_value = 1.0 - terminations[t]
            mask_traj = 1.0 - dones[t]

            delta = rewards[t] + self.gamma * next_values[t] * mask_value - values[t]
            gae = delta + self.gamma * self.lamda * mask_traj * gae

            advantages[t] = gae

        returns = advantages + values
        return advantages, returns

    def act(self, obs):
        obs = torch.as_tensor(obs, dtype = torch.float32, device=self.device)
        return self.actor.act(obs)

    def train(self, obs, global_obs, next_obs, dones, terminations, actions, rewards, old_log_probs):
        obs = torch.as_tensor(np.array(obs), dtype = torch.float32, device=self.device)
        global_obs = torch.as_tensor(np.array(global_obs), dtype = torch.float32, device=self.device)
        rewards = torch.as_tensor(np.array(rewards), dtype = torch.float32, device=self.device)
        next_obs = torch.as_tensor(np.array(next_obs), dtype = torch.float32, device=self.device)
        dones = torch.as_tensor(np.array(dones), dtype = torch.long, device=self.device)
        share_next_obs = next_obs.reshape(next_obs.shape[0], -1)
        next_global_obs = share_next_obs.unsqueeze(1).repeat(1, self.n_agents, 1)
        actions = torch.stack(actions).to(self.device).view(-1, 1)
        old_log_probs = torch.stack(old_log_probs).to(self.device).detach().view(-1, 1)

        advantages, returns = self.GAE(global_obs, next_global_obs, rewards, dones, terminations)
        returns = returns.view(-1, 1)
        obs = obs.view(-1, self.obs_dim)
        global_obs = global_obs.view(-1, self.global_obs_dim)
        advantages = advantages.view(-1, 1)
        advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)
        data_length = obs.size(0)
        for T in range(self.K_epochs):
            indices = torch.randperm(data_length).to(self.device)

            for start_index in range(0, data_length, self.batch_size):
                sample_indices = indices[start_index: start_index + self.batch_size]
                mb_obs = obs[sample_indices]
                mb_global_obs = global_obs[sample_indices]
                mb_actions = actions[sample_indices]
                mb_old_log_probs = old_log_probs[sample_indices]
                mb_returns = returns[sample_indices]
                mb_advantages = advantages[sample_indices]

                probs = self.actor(mb_obs)
                dist = Categorical(logits=probs)
                new_log_probs = dist.log_prob(mb_actions.squeeze(-1)).view(-1, 1)

                ratio = torch.exp(new_log_probs - mb_old_log_probs)

                surr1 = ratio * mb_advantages
                clipped_ratio = torch.clamp(ratio, 1 - self.epsilon, 1 + self.epsilon)
                surr2 = clipped_ratio * mb_advantages
                actor_loss = -torch.min(surr1, surr2).mean()

                entropy_loss = -self.c2_entropy * dist.entropy().mean()

                actor_loss += entropy_loss

                current_values = self.critic(mb_global_obs).view(-1, 1)
                critic_loss = self.c1_vf * nn.functional.mse_loss(current_values, mb_returns)

                self.actor_optimizer.zero_grad()
                actor_loss.backward()
                torch.nn.utils.clip_grad_norm_(self.actor.parameters(), 0.5)
                self.actor_optimizer.step()

                self.critic_optimizer.zero_grad()
                critic_loss.backward()
                torch.nn.utils.clip_grad_norm_(self.critic.parameters(), 0.5)
                self.critic_optimizer.step()

    def save(self, filename):
        """
        保存模型
        filename: 保存的文件路径，例如 'model_final.pth'
        """
        checkpoint = {
            'actor_state_dict': self.actor.state_dict(),
            'critic_state_dict': self.critic.state_dict(),
            'actor_optimizer': self.actor_optimizer.state_dict(),
            'critic_optimizer': self.critic_optimizer.state_dict()
        }
        torch.save(checkpoint, filename)
        print(f"Model saved to {filename}")

    def load(self, filename, evaluate=False):
        """
        加载模型
        filename: 文件路径
        evaluate: 如果是 True，只加载 Actor 用于演示；如果是 False，加载所有用于继续训练
        """
        checkpoint = torch.load(filename, map_location=self.device)

        # 1. 加载 Actor (必须的)
        self.actor.load_state_dict(checkpoint['actor_state_dict'])

        # 2. 如果要继续训练，还需要加载 Critic 和 优化器
        if not evaluate:
            self.critic.load_state_dict(checkpoint['critic_state_dict'])
            self.actor_optimizer.load_state_dict(checkpoint['actor_optimizer'])
            self.critic_optimizer.load_state_dict(checkpoint['critic_optimizer'])
            print(f"Full model loaded from {filename} (Ready to resume training)")
        else:
            # 如果只是预测，把模式设为 eval，冻结参数
            self.actor.eval()
            print(f"Actor loaded from {filename} (Ready for inference)")

数据收集以及训练

simple-spread包含顺序模式以及并行模式，区别就是对于每个智能体的状态以及动作选择是否统一进行，并行就是统一获取所有智能体的状态，同时返回动作要将所有智能体的动作一次性告诉环境。

这里选择并行模式，因此收到的数据以及返回的动作都是字典格式的，需要进行转换。

python 复制代码

from matplotlib import pyplot as plt
from pettingzoo.mpe import simple_spread_v3
from tqdm import tqdm
import numpy as np

from MADRL.MAPPO import MAPPO

env = simple_spread_v3.parallel_env(render_mode=None, continuous_actions=False)
agents = env.possible_agents
obs_dim = env.observation_space(agents[0]).shape[0]
act_dim = env.action_space(agents[0]).n
n_agents = len(agents)
model = MAPPO(obs_dim, act_dim, n_agents=n_agents)

episodes = 3000
T_step = 1024
scores = []
score = 0
obs_dict, _ = env.reset()
pbar = tqdm(range(episodes), desc="Training")
for episode in pbar:
    done = False
    observations, global_observations, actions, rewards, dones, terminations, next_observations, old_log_probs = [], [], [], [], [], [], [], []
    for t in range(T_step):
        obs_array = np.stack([obs_dict[agent] for agent in agents])
        share_obs = obs_array.reshape(1, -1).repeat(len(env.agents), axis=0)
        global_observations.append(share_obs)
        action, old_log_prob = model.act(obs_array)
        action_cpu = action.detach().cpu().numpy()
        action_dict = dict(zip(agents, action_cpu))
        next_observation, reward, termination, truncation, _ = env.step(action_dict)
        score += np.mean(list(reward.values()))
        observations.append(obs_array)
        actions.append(action)
        re_array = np.stack([reward[agent] for agent in agents])
        rewards.append(re_array)
        ter_array = np.stack([termination[agent] for agent in agents])
        tru_array = np.stack([truncation[agent] for agent in agents])
        done = np.bitwise_or(ter_array, tru_array)
        done_flag = np.any(done).astype(np.float32)
        dones.append(done_flag)
        terminations.append(ter_array)
        obs_array = np.stack([next_observation[agent] for agent in agents])
        next_observations.append(obs_array)
        old_log_probs.append(old_log_prob)
        obs_dict = next_observation
        if np.any(done_flag):
            obs_dict, _ = env.reset()
            scores.append(score)
            score = 0

    model.train(observations, global_observations, next_observations, dones, terminations, actions, rewards, old_log_probs)
    pbar.set_postfix(ep=episode, score=f"{(scores[-1] if scores else 0):.2f}", avg100=f"{np.mean(scores[-100:]):.2f}")

if np.mean(scores[-1000:]) >= -12:
    model.save("../../model/MAPPO-simple-spread-v3.pth")

def smooth(data, weight=0.99):
    """用于平滑曲线的函数 (Exponential Moving Average)"""
    last = data[0]
    smoothed = []
    for point in data:
        smoothed_val = last * weight + (1 - weight) * point
        smoothed.append(smoothed_val)
        last = smoothed_val
    return smoothed

# 使用方法：
smooth_scores = smooth(scores, weight=0.99)

plt.figure(figsize=(10, 5))
plt.plot(scores, alpha=0.3, color='lightblue', label='Raw Score') # 原始数据画成浅色背景
plt.plot(smooth_scores, color='blue', label='Smoothed Score')     # 平滑数据画成深色线条
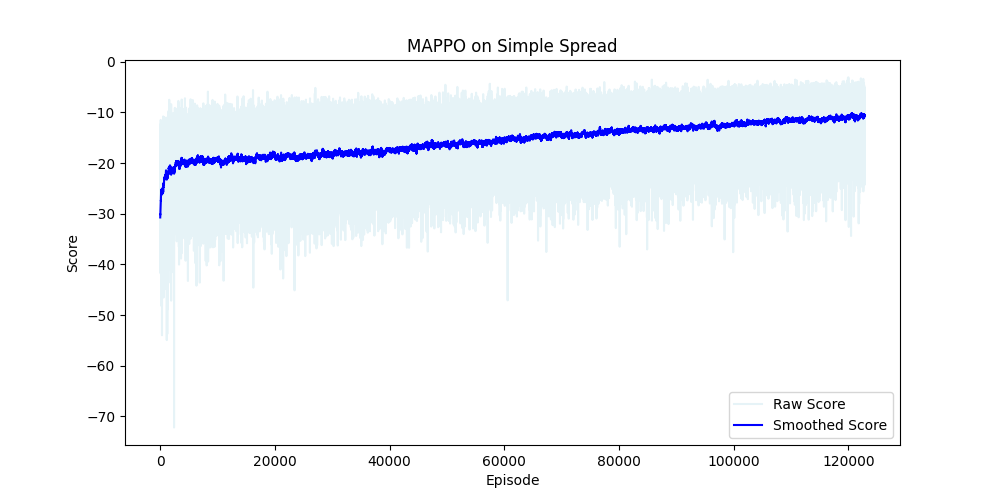
plt.title("MAPPO on Simple Spread")
plt.xlabel("Episode")
plt.ylabel("Score")
plt.legend()
plt.show()

训练结果

经过3000轮训练后(每轮1024步)，模型表现均值收敛在 − 10 -10 −10左右。