2025机器人与智能制造技术国际会议 (ISRIMT 2025)

重要信息

官网： https://ais.cn/u/IrQrua

**时间：**2025年12月12-14日

**地点：**中国-江苏常州

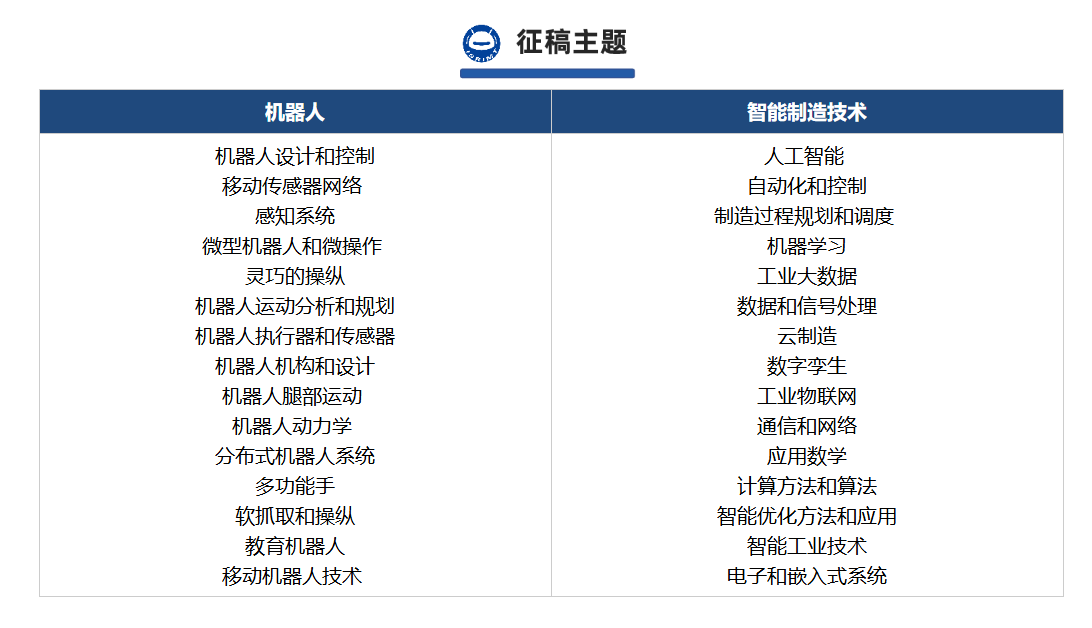
征稿主题

一、机器人与智能制造技术发展背景

智能制造作为工业 4.0 的核心方向，机器人技术则是智能制造落地的关键载体。2025 年机器人与智能制造技术国际会议（ISRIMT 2025）聚焦该领域前沿技术突破与工程应用创新，本文从技术原理、核心算法、工程实现等维度，拆解机器人与智能制造的核心知识点，覆盖运动控制、智能感知、数据驱动优化等关键方向。

二、核心技术体系：机器人与智能制造关键模块

2.1 技术模块全景表

技术模块	核心应用场景	关键技术点	技术挑战
机器人运动控制	工业机械臂轨迹规划、AGV 路径导航	逆运动学求解、PID 参数自整定、轨迹插补算法	高动态场景下的轨迹精度、多轴协同控制延迟
智能感知与识别	工件缺陷检测、物料分拣、人机协作避障	机器视觉（YOLO/CNN）、激光雷达点云处理、力觉传感融合	复杂光照 / 遮挡环境下的识别准确率、实时性平衡
智能制造数据挖掘	生产过程能耗优化、设备故障预测	时序数据分析、机器学习建模、工业大数据清洗	多源异构数据整合、小样本故障数据建模
人机协作安全控制	协作机器人人机交互、柔性装配	碰撞检测算法、力位混合控制、安全阈值动态调整	安全与作业效率的平衡、非结构化环境适配

2.2 机器人运动控制：逆运动学求解与轨迹规划

2.2.1 6 轴机械臂逆运动学核心原理

6 轴串联机械臂的逆运动学求解是实现精准轨迹控制的基础，其核心是通过末端执行器的位姿（位置 + 姿态）反推各关节的角度。常见解法包括解析法（针对结构对称的机械臂，如 PUMA560）和数值法（如牛顿 - 拉夫逊迭代法）。

2.2.2 Python 实现简化版逆运动学求解（以 3 轴机械臂为例）

python

运行

import math
import numpy as np

class ThreeAxisArm:
    def __init__(self, link_lengths):
        """
        初始化3轴机械臂参数
        :param link_lengths: 列表，包含3个连杆长度 [l1, l2, l3]
        """
        self.l1, self.l2, self.l3 = link_lengths

    def inverse_kinematics(self, x, y, z):
        """
        求解3轴机械臂逆运动学（简化版，仅考虑位置，忽略姿态）
        :param x, y, z: 末端执行器笛卡尔坐标
        :return: 关节角度 [theta1, theta2, theta3]（弧度）
        """
        # 关节1：绕Z轴旋转，theta1由x,y确定
        theta1 = math.atan2(y, x)
        
        # 计算投影到XY平面的距离
        r = math.hypot(x, y)
        # 关节2和3的求解（平面2轴问题）
        D = (r**2 + (z - self.l1)**2 - self.l2**2 - self.l3**2) / (2 * self.l2 * self.l3)
        # 限制D的范围在[-1,1]，避免数值误差
        D = max(min(D, 1.0), -1.0)
        theta3 = math.atan2(-math.sqrt(1 - D**2), D)
        
        # 计算关节2角度
        k1 = self.l2 + self.l3 * math.cos(theta3)
        k2 = self.l3 * math.sin(theta3)
        theta2 = math.atan2((z - self.l1), r) - math.atan2(k2, k1)
        
        return [theta1, theta2, theta3]

# 示例：3轴机械臂逆解计算
if __name__ == "__main__":
    arm = ThreeAxisArm([0.5, 1.0, 0.8])  # 连杆长度l1=0.5, l2=1.0, l3=0.8
    end_x, end_y, end_z = 1.2, 0.8, 1.0  # 末端坐标
    joint_angles = arm.inverse_kinematics(end_x, end_y, end_z)
    print("关节角度（弧度）：", joint_angles)
    print("关节角度（角度）：", [math.degrees(angle) for angle in joint_angles])

2.3 智能制造中的数据驱动故障预测

2.3.1 基于 LSTM 的设备故障预测原理

在智能制造产线中，设备振动、温度、电流等时序数据蕴含故障前兆信息。LSTM（长短期记忆网络）能够捕捉时序数据的长期依赖关系，通过历史数据训练模型，实现设备故障的提前预测。

2.3.2 Python 实现 LSTM 故障预测（简化版）

python

运行

import numpy as np
import pandas as pd
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense, Dropout
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split

# 1. 数据预处理（模拟设备时序数据）
def generate_simulation_data(n_samples=10000, time_steps=20):
    """生成模拟设备运行时序数据：正常/故障标签+多维度传感器数据"""
    # 正常数据：平稳波动；故障数据：趋势性变化+噪声
    normal_data = np.random.normal(loc=0.5, scale=0.1, size=(int(n_samples*0.9), time_steps, 3))
    fault_data = np.random.normal(loc=0.8, scale=0.2, size=(int(n_samples*0.1), time_steps, 3))
    # 标签：0=正常，1=故障
    normal_labels = np.zeros(int(n_samples*0.9))
    fault_labels = np.ones(int(n_samples*0.1))
    
    data = np.concatenate([normal_data, fault_data], axis=0)
    labels = np.concatenate([normal_labels, fault_labels], axis=0)
    
    # 打乱数据
    shuffle_idx = np.random.permutation(n_samples)
    data = data[shuffle_idx]
    labels = labels[shuffle_idx]
    
    return data, labels

# 2. 构建LSTM模型
def build_lstm_model(input_shape):
    model = Sequential()
    model.add(LSTM(units=64, return_sequences=True, input_shape=input_shape))
    model.add(Dropout(0.2))
    model.add(LSTM(units=32, return_sequences=False))
    model.add(Dropout(0.2))
    model.add(Dense(units=16, activation='relu'))
    model.add(Dense(units=1, activation='sigmoid'))  # 二分类：故障/正常
    
    model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
    return model

# 3. 模型训练与验证
if __name__ == "__main__":
    # 生成数据
    time_steps = 20  # 时间步长：用前20个时刻数据预测故障
    X, y = generate_simulation_data(n_samples=10000, time_steps=time_steps)
    
    # 数据归一化（针对每个特征维度）
    scaler = MinMaxScaler(feature_range=(0, 1))
    X_reshaped = X.reshape(-1, 3)  # 展平为(样本数*时间步, 特征数)
    X_scaled = scaler.fit_transform(X_reshaped)
    X_scaled = X_scaled.reshape(-1, time_steps, 3)  # 恢复原形状
    
    # 划分训练集/测试集
    X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
    
    # 构建并训练模型
    model = build_lstm_model(input_shape=(time_steps, 3))
    history = model.fit(
        X_train, y_train,
        batch_size=32,
        epochs=10,
        validation_data=(X_test, y_test)
    )
    
    # 模型评估
    test_loss, test_acc = model.evaluate(X_test, y_test)
    print(f"测试集准确率：{test_acc:.4f}")
    print(f"测试集损失：{test_loss:.4f}")

三、技术融合与落地关键点

3.1 多技术模块协同优化

机器人与智能制造系统并非单一技术的堆叠，而是运动控制、智能感知、数据挖掘等模块的深度协同。例如：

• 视觉识别模块输出的工件位置偏差，需实时反馈给运动控制模块，调整机械臂轨迹；
• 故障预测模块的预警信号，触发人机协作模块的安全策略调整，降低产线停机风险。

3.2 工程落地的核心考量

考量维度	关键指标	优化方向
实时性	控制周期（≤10ms）、数据处理延迟（≤50ms）	轻量化算法、边缘计算部署
鲁棒性	极端工况下识别准确率（≥99%）、控制稳定性	多传感器融合、异常值剔除
可扩展性	新增产线适配时间（≤72h）	模块化代码架构、标准化接口

四、未来技术演进方向

从 ISRIMT 2025 的技术研讨趋势来看，机器人与智能制造技术将向以下方向突破：

1. 端边云协同：边缘端实现实时控制，云端完成全局优化与模型迭代，提升系统整体效率；
2. 具身智能机器人：融合环境感知、自主决策、柔性操作，适配非结构化智能制造场景；
3. 低碳化智能制造：通过机器人能耗优化、产线调度算法，降低智能制造全生命周期碳排放；
4. 数字孪生驱动：构建机器人 - 产线数字孪生体，实现虚拟调试、实时监控与预测性维护。

五、国际交流与合作机会

作为国际学术会议，将吸引全球范围内的专家学者参与。无论是发表研究成果、聆听特邀报告，还是在圆桌论坛中与行业大咖交流，都能拓宽国际视野，甚至找到潜在的合作伙伴。对于高校师生来说，这也是展示研究、积累学术人脉的好机会。