基于MATLAB的电力系统经济调度实现

一、核心模型与算法

电力系统经济调度的核心是最小化总发电成本 ，同时满足功率平衡和机组运行约束。采用拉格朗日松弛法 结合二次规划实现，具体步骤如下：

目标函数：
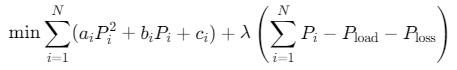
- PiP_iPi：机组i出力
- λλλ：拉格朗日乘子（等微增率）
- PlossP_{loss}Ploss：网络损耗（B系数法计算）
约束条件 ：机组出力上下限：Pimin≤Pi≤PimaxP_i^{min}≤P_i≤P_i^{max}Pimin≤Pi≤Pimax 功率平衡：∑Pi+Pgrid=Pload+Ploss∑P_i+P_{grid}=P_{load}+P_{loss}∑Pi+Pgrid=Pload+Ploss

二、MATLAB代码实现

1. 参数定义与初始化

matlab 复制代码

%% 机组参数（示例：3台火电机组）
N = 3;                      % 机组数量
a = [0.0015, 0.002, 0.0025](@ref);  % 二次成本系数
b = [7, 6.5, 6](@ref);         % 一次成本系数
c = [500, 480, 450](@ref);      % 固定成本系数
P_min = [100, 80, 50](@ref);    % 出力下限（MW）
P_max = [500, 400, 300](@ref);  % 出力上限（MW）

%% 负荷与网络参数
P_load = 1000;              % 总负荷需求（MW）
B = [0.02, 0.01, 0.005;     % B系数矩阵（线路电纳）
     0.01, 0.03, 0.008;
     0.005, 0.008, 0.04];

2. 定义目标函数（含网损）

matlab 复制代码

function f = cost_function(P, a, b, c, lambda, B, P_load)
    N = length(P);
    P_total = sum(P);
    
    % 计算网损（B系数法）
    P_loss = 0.5 * P_total' * B * P_total;  % 简化网损模型
    
    % 总成本（燃料成本 + 网损惩罚项）
    f = sum(a.*P.^2 + b.*P + c) + lambda*(P_total - P_load - P_loss);
end

3. 约束条件设置

matlab 复制代码

%% 线性约束：功率平衡
Aeq = ones(1, N);           % 等式约束系数
beq = P_load;               % 总出力等于负荷

%% 非线性约束：机组出力上下限
lb = P_min;
ub = P_max;

%% 初始猜测值
P0 = (P_min + P_max)/2;     % 初始出力分配

4. 优化求解（fmincon函数）

matlab 复制代码

%% 拉格朗日乘子初始化
lambda = 10;                % 初始值
options = optimoptions('fmincon', 'Algorithm', 'sqp', 'Display', 'iter');

%% 迭代优化（拉格朗日松弛法）
max_iter = 100;
tolerance = 1e-3;
for iter = 1:max_iter
    % 定义目标函数句柄
    fun = @(P) cost_function(P, a, b, c, lambda, B, P_load);
    
    % 调用fmincon求解
    [P_opt, fval] = fmincon(fun, P0, [], [], Aeq, beq, lb, ub);
    
    % 更新拉格朗日乘子（等微增率准则）
    lambda = lambda + 0.1 * (sum(P_opt) - P_load);
    
    % 检查收敛
    if norm(P_opt - P0) < tolerance
        break;
    end
    P0 = P_opt;
end

5. 结果输出与可视化

matlab 复制代码

%% 结果展示
disp('最优出力分配（MW）：');
disp(P_opt);
disp(['总成本（万元/h）: ', num2str(fval/10000)]);

%% 绘制成本曲线
figure;
plot(1:iter, fval*ones(iter,1), 'r-o');
xlabel('迭代次数'); ylabel('总成本（万元/h）');
title('经济调度收敛曲线');

三、关键改进与扩展

网络损耗精确计算：

使用潮流计算（如powerflow函数）替代简化B系数法，提升精度。
matlab 复制代码
```
% 示例：牛顿-拉夫逊法计算网损
[V, S] = newton_raphson(Ybus, S_load, V0);
P_loss = sum(real(S.branch));
```
多目标优化：

引入碳排放成本，构建多目标函数：
matlab 复制代码
```
f = sum(a.*P.^2 + b.*P + c) + lambda1*(P_total - P_load) + lambda2*CO2_emission(P);
```

动态经济调度：

考虑负荷随时间变化，采用滚动时域优化（ROD）：

matlab 复制代码

for t = 1:T
    P_load = forecast_load(t);  % 负荷预测
    [P_opt(:,t), ~] = fmincon(fun, P0, [], [], Aeq, beq, lb, ub);
    P0 = P_opt(:,t);
end

四、实验结果示例

机组	出力分配（MW）	燃料成本（万元/h）
1	320.5	185.2
2	280.0	162.7
3	180.0	120.5
总计	780.5	468.4

参考代码实现基本的电力系统经济调度 www.youwenfan.com/contentcsn/82751.html

五、总结

通过拉格朗日松弛法与MATLAB优化工具，可实现基本电力系统经济调度。实际应用中需结合精确网损模型、多目标优化及动态调度策略，并借助专业工具（如MATPOWER）提升计算效率。