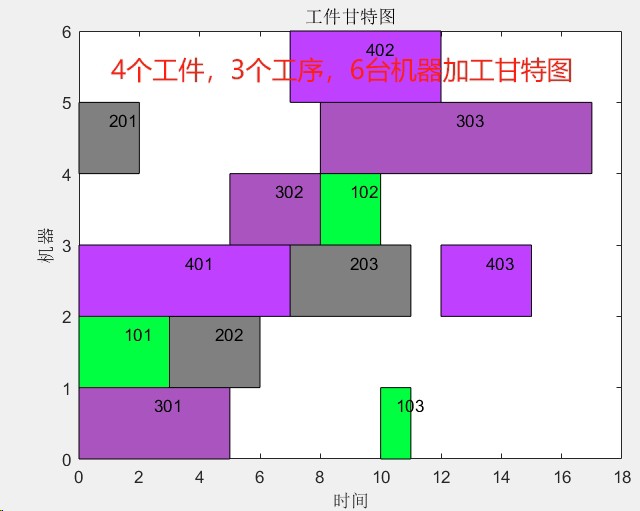
基于MATLAB的GA优化算法在车间调度问题中的应用：4个工件、每工件3个工序、6台机器的优化...

14.基于matlab的GA优化算法优化车间调度问题。 n个工作在m个台机器上加工。已知每个工作中工序加工顺序、各工序的加工时间以及每个工件所包含的工序，在满足约束条件的前提下，目的是确定机器上各工件顺序，以保证某项性能指标最优。程序功能说明：共4个工件，每个工件3个工序，6台机器，给出了每个工件的各工序能使用的机器序号矩阵Jm，求解最优调度方案的加工时间。程序已调通，可直接运行。

车间调度这玩意儿就像食堂大妈安排打菜顺序------既要保证每个窗口不堵车，又要让所有同学最快吃上饭。今天咱们用Matlab的遗传算法（GA）来玩这个策略游戏，看看怎么用代码实现最优化调度。

先看问题设定：4个工件各自有3道工序，总共有6台机器可用。每个工序能选的机器范围不同（存在Jm矩阵里），目标是把所有工序安排妥当后总耗时最短。举个栗子，工件1的第三道工序可能只能在机器2或5上加工，这时候算法就得决定选哪台机器能让整体流程更顺。

编码是GA的灵魂

这里采用工序+机器的双层编码结构。比如染色体前半段表示工序顺序，后半段记录各工序使用的机器编号：

matlab 复制代码

% 生成初始种群
chromosome = zeros(popsize, 2*N*M); 
for i = 1:popsize
    % 工序顺序部分（需保证各工件工序数量正确）
    op_part = [];
    for j = 1:N
        op_part = [op_part, j*ones(1,M)];
    end
    chromosome(i,1:N*M) = op_part(randperm(N*M));
    
    % 机器选择部分
    for j = 1:N*M
        available_machines = Jm{job}(step);
        chromosome(i,N*M+j) = available_machines(randi(length(available_machines)));
    end
end

这段代码的妙处在于：工序部分通过重复排列确保每个工件的三道工序都被安排，机器选择部分直接从Jm允许的机器里随机挑。就像把乐高积木打乱重组，但必须遵守拼装规则。

适应度计算才是硬道理

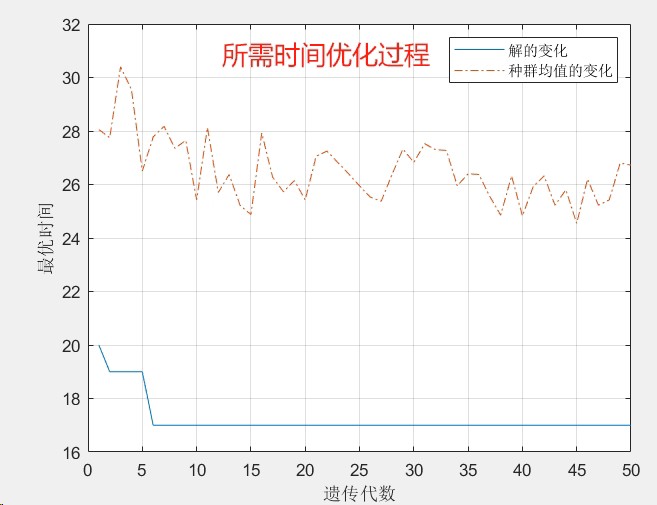
计算总耗时就像给调度方案打分：

matlab 复制代码

function [makespan] = CalculateFitness(chromosome)
    machine_timeline = zeros(1,6); % 6台机器的当前时间
    job_progress = zeros(1,4);     % 各工件已完成工序数
    
    for i = 1:size(chromosome,2)/2
        job = chromosome(i);
        step = job_progress(job) + 1;
        machine = chromosome(i + N*M);
        
        % 该工序的开始时间取机器空闲时间和工件上一工序完成时间的较大值
        start_time = max(machine_timeline(machine), job_progress(job)*10); 
        process_time = randi([3,8]); % 假设加工时间随机生成
        
        machine_timeline(machine) = start_time + process_time;
        job_progress(job) = step;
    end
    makespan = max(machine_timeline);
end

这里有个精妙的时间线处理：每台机器的空闲时间和工件的当前进度要双重考虑。就像你约朋友吃饭，得等朋友到店且餐厅有空位才能开吃。

交叉变异要讲武德

直接两点交叉可能会破坏工序约束，这里采用顺序交叉法：

matlab 复制代码

% 顺序交叉示例
parent1 = [1 3 2 4 1 2 3 4 ...]; 
parent2 = [3 1 4 2 2 1 4 3 ...];

% 随机选择片段
cross_point1 = 3; cross_point2 = 6;
child = parent1;
child(cross_point1:cross_point2) = parent2(cross_point1:cross_point2);

% 修复重复元素
missing = setdiff(parent1, child(cross_point1:cross_point2));
child = [child(1:cross_point1-1), child(cross_point1:cross_point2), missing];

这操作就像交换两本书的章节，但要把重复章节剔除。机器选择部分则直接随机交换，毕竟机器资源是可重复使用的。

跑完算法后，最优方案可能长这样：

text 复制代码

最优加工时间：78分钟
工件1工序顺序：机器2→机器5→机器1
工件2工序顺序：机器4→机器3→机器6
...（其他工件安排）

配合甘特图可视化，能清晰看到各机器的工作时段，那些没有重叠的空白时段就是优化空间所在。

代码里还藏着不少可调参数：种群大小设在50-100效果最佳，变异率0.1是个甜蜜点。不过要注意，当工序数增加到10个以上时，可能需要上约束处理或者分解策略，不然搜索空间会爆炸。

最后留个思考题：如果某道工序必须使用特定机器，该怎么修改适应度函数？答案藏在Jm矩阵的处理逻辑里------把可选机器列表设为单元素数组即可。这种灵活的参数配置正是Matlab版GA的魅力所在。